справочник математика

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рыбинский государственный авиационный технический университет им. П. А. Соловьева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

среднеквадратического отклонения, т.е. σ x = S =

.pdf

Скачиваний:

Добавлен:

20.03.2016

Размер:

484.12 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

3. D( X ± Y ) = D( X ) + D(Y )

σ x =

- среднее

квадратическое отклонение (в линейных

единицах).

kв

= σ x

коэффициент вариации

(изменчивости)

(в

относительных единицах).

M [( X - M ( X )k )

μk (x) =

- центральный момент k – того

−∞

(x - M ( X ))

∫

f (x) dx

+∞

μ2 (x) = Dx .

порядка, в частности

kA =

μ3 (x)

- коэффициент асимметрии

Ek =

μ4 (х)

− 3

- эксцесс (коэффициент

островершинности),

σ 4

частности для нормального (Гауссово) распределения Ek = 0 .

14.5. Законы распределения непрерывных случайных величин

14.5.1. Нормальное (Гауссово) распределение

				1			− ( x−a )2
	f (x) =			1		× e		2σ x
								2
		σ
		σ	х		2π
			х					a = mx -
- закон нормального распределения, где								a = mx -	математическое
ожидание;	D( X ) = σ x2 - дисперсия;							f (x) =	f (x, mx ,σ x )	-
двухпараметрическое распределение.

x ~ N (mx ,σ x ) - обозначение случайной величины, имеющей нормальное распределение;

	β − а			α − а
P(λ < x < β ) = Ф			− Ф
	σ			σ
	σ	х		σ	х

вероятность того,

что Х

примет

значение,

принадлежащее

интервалу (α , β ) , где Ф(х) =

− х2

∫ е 2

- функция Лапласа;

2π

операции нормирования и центрирования:

x − m

{M (x) − mx

} = 0 ,

σ x

x − m

= 1;

σ x

X − a

< δ ) = 2Ф

- вероятность того, что абсолютная величина отклонения меньше положительного числа δ ;

me = a - медиана нормального распределения.

14.5.2. Равномерное (равновероятное, прямоугольное) распределение

	1	, a ≤ x ≤ b


f (x) = b	− a
		b < x < a
0,

- закон равномерного распределения;

+∞	1	a	x	1		x − a
F (x) = ∫		dt = ∫ 0dt + ∫			dt =
				b − a		b − a
−∞ b − a		−∞	a

- функция распределения;

mx = a + b - математическое ожидание; 2

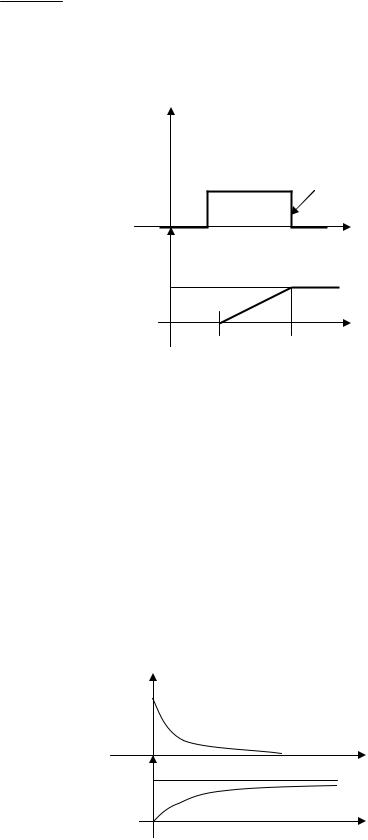
Dx = (b - a)2 - дисперсия; 12

kА = 0 .

f(x)

h=1/(b-a)

F(x)

14.5.3. Показательное (экспоненциальное) распределение

0, x < 0

f (x) = λ −λx ³e , x 0

- показательное распределение вероятностей непрерывной случайной величины;

f(x)

F(x)	1	x
	1
	0	x

F (x) = 1 - e− λx - функция распределения показательного закона;

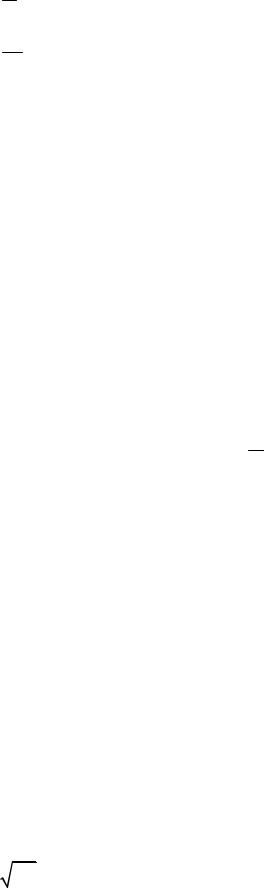
mx = λ1 - математическое ожидание;

D= 1 - дисперсия;

xλ2

σ =	1	= m		-	характеристическое	свойство	показательного
	λ
x			x

распределения.

15.МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

15.1.Статистические оценки параметров распределения

15.1.1.Оценка математического ожидания

(выборочной средней)

Математическое ожидание: X Г = mx = ∑ xi pi - генеральная средняя

i=1

Случайная величина - оценка математического ожидания

mx = X B =

∑ xi

- выборочная средняя

n i=1

X =

∑ xi mi

∑

xi mi

= ∑ xi Pi

, где

- частота отдельных

n i=1

i=1 n

i=1

значений

15.1.2. .Оценка дисперсии

Генеральная дисперсия:

			1	N				2
σ 2 = D		=				− X	Г )
				∑	x

	Г		N i=1(		i

Генеральное среднеквадратическое отклонение: σ ч = 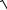Dx

Выборочная дисперсия:

D = 1 ∑ (x − X )2

= 1 ∑ (x − X )2 m = ∑ (x − X B )2

B i

n i=1

i=1

σ В = 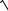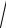DВ - выборочное среднеквадратическое отклонение.

Удобная формула оценки дисперсии через оценку второго начального момента

DB = (α 2 ) − ( X )2 = 1 ∑k (xi )2 − ( X )2

n i=1

15.2. Точечные оценки точности оценок (статистик) генеральных числовых характеристик θx

{x1 , x2 ,K, xN } θ x ; {x11 , x21,K, xn1} θ x*1; −

{x12 , x22 ,K, xn2} θ x*2 ; -оценки статистических

LLLLLLLLLL

{x1k , x2k ,K, xnk } θ xk* .

характеристик

θ *xi - с.в., характеризуемая законами распределения и числовыми

характеристиками распределения (обычно математическим ожиданием и дисперсией).

1. Оценка называется состоятельной, если она сходится по

вероятности к оцениваемой характеристике lim P(			θ − θ	< ε ) = 1, ε > 0 .
вероятности к оцениваемой характеристике lim P(			θ − θ	< ε ) = 1, ε > 0 .
	n→∞		i
	n→∞
2.Оценка называется несмещенной, если M [θ		] = θ .
	i
M [θ	] − θ = - смещение, систематическая погрешность (от
i

смещенности). Асимптотически несмещенная оценка lim M (θ − θ ) = 0 .
n→∞	i

3.Оценка называется эффективной, если при используемом методе ее

расчета выполняется условие

D[θ ] = min .

Пример 1. Оценка

B является несмещенной, а ее дисперсия

уменьшается при усреднении в n раз:

M X

= M

= m

= X

∑

n i=1

		1	n		1		D
D[ X ] = D[				x ] =		nD =
			∑				В	.
					n2
	В	n i=1		i		В	n

Если

х~ N (mx,σ x )

- эффективная оценка.

Пример 2. Оценка дисперсии DB = M [

∑ (xi - X B )2 ] является

смещенной:

n − 1

n i=1

Доказано, что D =

- т.е. данный алгоритм дает смещенную

DВ

оценку дисперсии:

n .

Исправленная (несмещенная) оценка дисперсии

nDB

= S 2 =

∑ (xi - X B )2 .

n -

n -1

1 i=1

На практике исправленной оценкой дисперсии пользуются при n<30.

15.3. Интервальная оценка точности (надежность) генеральных математического ожидания и дисперсии

Доверительный интервал - интервал значений, в котором с заданной доверительной вероятностью (обычно назначают

β = 0.9; 0.95; 0.99 ) находится истинное значение оцениваемой статистической характеристики θx :

θ -θ

< δ ] = β P[θ - δ < θ < θ + δ ] = β .

t ×σ

Радиус доверительного интервала равен: δ =

t ×σ

где t- аргумент, соответствующий значению функции Лапласа, равной β / 2 ; σ θ - среднеквадратическое отклонение θx (его оценка).

Доверительный интервал случаен (зависит от конкретных выборок): случайно его положение на числовой оси и случайна его длина.

При n → ∞ δ → 0 , а при β → 1 δ → ∞ .

1. Доверительный интервал для оценки математического ожидания

P(X - δ < mx

< X + δ )= Ф

X + δ

- mX

- Ф

X -δ

- mX

σ x

tσ

t =

δ =

= Ф

- Ф

= 2Ф

= β

σ x

Здесь t рассматривается как аргумент табулированной функции

распределения Лапласа, при котором она равна значению

β / 2 .

Значение генерального среднеквадратического отклонения σ x редко

известно,

поэтому

обычно

формуле

используют оценку

Замечание. Практически важной может быть задача определения объема выборки, которая обеспечит заданный радиус доверительного

интервала: n ³	t 2σ 2
	x		.
	δ 2			результаты при малых объемах выборки n и
Более точные
неизвестном σ x		дает использование распределения Стьюдента: для
				- mx		, имеющей распределение Стьюдента с k=n-1
переменной -	t =	X

			S
					n

степенями свободы отклонение (X~ N (mx ;σ x ) ) Тогда доверительный

интервал при неизвестном среднеквадратическом

отклонении

× S

= β ,

определяется следующим образом: P X -

< mx

X +

где tβ аргумент табулированного распределения Стьюдента.

2. Доверительные интервалы оценки среднеквадратического отклонения

Пусть вновь x~ N (mx ,σ x ) , и σ x - неизвестно, а S =

∑n (xi -

σ x - δ

< δ ] = β

S − δ < σ x < S + δ

n -1 i=1

Тогда P[

S (1 − q) < σ x < S (1 + q) ,

где

q = δ .

Доказано, что q имеет табулированное распределение χ2 , независящее от параметров mx и σx исходного распределения, но зависящее от объема выборки и доверительной вероятности. Вычислив по выборке S, находим по таблице q, определяем границы доверительного интервала.

16. ДИСКРЕТНАЯ МАТЕМАТИКА И ЧИСЛЕННЫЕ МЕТОДЫ

16.1. Дискретная математика

Таблицы истинности

P Q P Ù Q P Ú Q P ® Q P « Q P | Q P ↓ Q P Å Q

0	0	0	0	1	1	1	1	0
0	1	0	1	1	0	1	0	1
1	0	0	1	0	0	1	0	1
1	1	1	1	1	1	0	0	0

X Y					Импликация Конверсия		Контрапозиция Конверсия
X Y			X	Y	Импликация Конверсия		Контрапозиция Конверсия
					X → Y
					X → Y	импликации Y		→ X	контрапозиции
						Y → X
						Y → X				X	→ Y
0	0	1		1	1	1	1		1
0	1	1		0	1	0	1		0
1	0	0		1	0	1	0		1
1	1	0		0	1	1	1		1

Отношение строгого порядка - бинарное отношение на множестве, если оно

не рефлексивно, антирефлексивно; антисимметрично, транзитивно.

Отношение нестрогого порядка - бинарное отношение на множестве, если оно

рефлексивно, антисимметрично, транзитивно.

Таблица Кэли: *- операция, a, b, c - элементы множества.

*	a	b		c
a	a * a	a * b	a * c
b	b * a	b * b	b * c
c	c * a	c * b	c * c
c	c * a	c * b	c * c

16.2.Численные методы

16.2.1.Решение дифференциальных уравнений

1.Метод Эйлера (первого порядка)

Расчётный шаг: h =					b − x0		,
Расчётный шаг: h =						n	,
						n
расчётные точки (узлы) –							равноотстоящие точки xk = x0 + kh, k = 0,1,2,...
Цель –		построение таблицы

x	x0	x1	…	xn=b
y	y0	y1	…	yn=y(b)

yk +1 = yk + hf (xk , yk ).

2. Метод Рунге-Кутта Бόльшая точность метода (по сравнению с методом Эйлера) при

нахождении приближённого решения ЗК для д.у.-1 достигается за счёт усложнения разностной схемы:

= y

+ 2k

+ k

k1 = f (xi , yi ),

hk1

f xi

, yi

hk2

f xi

, yi

= f (xi + h, yi + hk3 ).

16.2.2. Вычисление определённых интегралов

1.Формулы прямоугольников: h = b − a .

				n					h
Л П	n		П П	n	П	n			h
I ≈ h∑ f (xi 1 ) , I				≈ h∑ f (xi ) , I		≈ h∑ f x		−		.
I ≈ h∑ f (xi 1 ) , I				≈ h∑ f (xi ) , I		≈ h∑ f x		−		.
	i=1	−		i=1		i=1	i		2

2.Формула трапеций

f (a) +

f (b)

n−1

b − a

n−1

≈ h

+ ∑ f (xk

)

, I

≈

f (a) + f (b)

+ 2∑

k =1

3.Формула Симпсона

I C ≈

( y

+ y

+ 2( y

+ y

+ ... + y

2 n−2

) + 4( y

+ y

+ ... + y

2 n−1

))

2 n

I C ≈

b − a

( y

+ y

+ 2( y

+ y

+ ... + y

2 n−2

) + 4( y

+ y

+ ... + y

2 n−1

2 n

16.2.3. Решение алгебраических уравнений

f (x) = 0, x [a, b]. Метод хорд и касательных. Рекуррентные формулы:

f (x )

))

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.03.2016681.98 Кб252Создание и обработка звука (Павлов).doc
#
08.03.201512.88 Кб24СопроМат правила.docx
#
18.08.201983.46 Кб2Социологическое исследование.doc
#
25.08.201971.68 Кб4Спецификация программных требований.doc
#
27.09.2019160.65 Кб25СПО ЛЕКЦИИ.docx
#
20.03.2016484.12 Кб36справочник математика.pdf
#
08.03.2015115.2 Кб8средства и методы ук.doc
#
23.09.2019149.5 Кб3Стандарт обр по ИЯ.doc
#
08.03.2015243.71 Кб16Стандарт_СТП 1.01-2002.doc
#
08.03.2015203.78 Кб57Стандарт_СТП 1.01-2002.doc
#
08.05.2019243.71 Кб14Стандарт_СТП 1.01-2002.doc