справочник математика

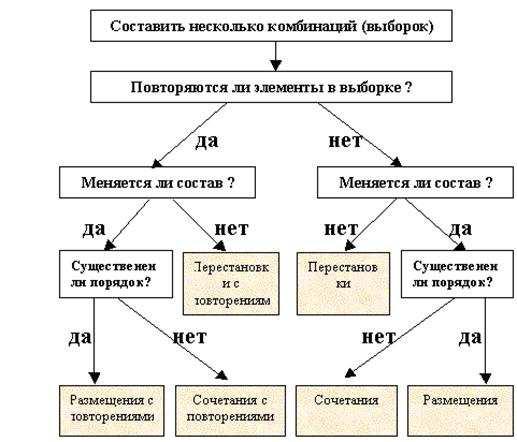
1. Размещения.

Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.

Число размещений без повторений из n по m (n различных элементов)

вычисляется по формуле:

Аnm = n × (n -1) × (n - 2) ×... × (n - m +1)

Размещениями с повторениями из n элементов по m называются

упорядоченные m-элементные выборки, в которых элементы могут

повторяться. Число размещений с повторениями вычисляется по формуле:

А~m = nm n

2. Перестановки

Перестановками из n элементов называются размещения из этих n элементов по n (Перестановки - частный случай размещений).

Число перестановок без повторений (n различных элементов)

вычисляется по формуле:

Pn = n !

Число перестановок c повторениями (k различных элементов, где элементы могут повторяться m1, m2, …, m k раз и m1 + m2 +… + m k = n, где n - общее количество элементов) вычисляется по формуле:

3. Сочетания

Сочетаниями из n элементов по m элементов называются комбинации,

составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов).

Число сочетаний без повторений (n различных элементов, взятых по m)

вычисляется по формуле:

Число сочетаний c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться) вычисляется по формуле:

C~m = (n + m − 1)! n m !×(n -1)!

14. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

14.1.Классическое определение вероятности

Вероятность случайного события можно определить как

P( A) = m , n

где m – число исходов испытания, которое благоприятствует появлению события A, n – общее число исходов испытания.

Сумма вероятностей событий A1 , A2 ,..., An , образующих полную группу, равна 1 (условие полноты группы событий).

P( A1 ) + P( A2 ) + ... + P( An ) = 1.

Противоположными называют два единственно возможных события, образующих полную группу.

P( A) + P( A) = 1, P( A) = 1 − P( A) .

14.2. Основные теоремы

Формула вероятности произведения двух зависимых событий.

P( AB) = P( A) × P(B / A) = P(B) × P( A / B)

Формула вероятности произведения двух независимых событий: P( AB) = P( A) × P(B) .

Формула вероятности произведения нескольких зависимых событий:

P( A1 , A2 , A3 ,...An ) = P( A1 )P( A2 | A1 ) × P( A3 | A1 A2 ) ×... × P( An | A1 A2 ...An−1 )

Формула вероятности произведения нескольких независимых событий:

P( A1 , A2 , A3 ,...An ) = P( A1 )P( A2 ) × P( A3 ) ×... × P( An ) .

Теоремы о сложении вероятностей событий:

P( A + B) = P( A) + P(B) - для несовместных событий

Р( А + В) = Р( А) + Р(В) − Р( АВ) - для совместных событий Замечание. Совместные события A и B могут быть зависимыми или независимыми. Для независимых и совместных событий:

Р( А + В) = Р( А) + Р(В) - Р( А) × Р(В), где Р( АВ) = Р( А) × Р(В).

Для зависимых и совместных событий:

Р( А + В) = Р( А) + Р(В) - Р( А) × Р(B / A), Р( АВ) = Р( А) × Р(B / A).

n

Формула полной вероятности P( A) = ∑P(H i ) × P( A | H i ) .

i=1

Формула вероятности гипотез (формула Байеса):

= P(H ) × P( A | H ) P(Hi | A) i i

∑P(Hi ) × P( A | Hi )

i

14.3.Повторение испытаний

14.3.1.Формула Бернулли

Вероятность того, что событие наступит k раз в n испытаниях, в каждом из которых вероятность появления событии одинаковая, (если n и k невелики), определяется как:

14.3.2. Локальная теорема Лапласа

Если n и k велики:

F(x) – является универсальной характеристикой и для непрерывных и для дискретных одномерных случайных величин и описывает вероятность события P( X < x) :

F (x) = P( X < x) .

Свойства функции распределения:

1.0 ≤ F (x) ≤ 1;

2.F (+∞) = P(x < +∞) = 1 ;

3.F (-¥) = P(x < -¥) = 0 ;

4.P( X ³ x) = 1 - F (x) - вероятность противоположного события;

5.P(a ≤ x ≤ b) = F (b) − F (a) - вероятность попадания в интервал

значений.

6.x2 > x1 F (x2 ) ³ F (x1 )

14.4.2.Плотность вероятности (дифференциальный закон) распределения непрерывной случайной величины

f (x) = F ′(x)

Свойства плотности вероятности

1. f (x) ³ 0 ;

+∞

2.∫ f (x)dx = 1 - условие нормировки (единичная площадь под кривой

−∞

распределения, полнота группы событий);

x

3.F (x) = ∫ f (t)dt - выражение функции распределения через

−∞

плотность;

b

4. P(a ≤ x ≤ b) = ∫ f (x)dx = F (b) − F (a) - вероятность попадания в

a

интервал значений.

14.4.3. Числовые характеристики распределения случайной величины

1. Математическое (безусловное) ожидание случайной величины.

Свойства математического ожидания

1.M ( X ) = C ×1 = C ;

2.M (CX ) = C × mx ;

3.M ( X + Y ) = M ( X ) + M (Y ) ;

4.M ( X ) = mx × my - если x и y независимые случайные величины;

α0 = 1

α1 (x) = mx

2.Дисперсия (безусловная) случайной величины.

Удобная формула расчета дисперсии: D( Х ) = M ( Х 2 ) - [M ( Х )]2

Свойства дисперсии

1.D( X ) = (C - C)2 ×1 = 0;

2.D(CX ) = C 2 × Dx ;