Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рыбинский государственный авиационный технический университет им. П. А. Соловьева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

справочник математика

.pdf

Скачиваний:

Добавлен:

20.03.2016

Размер:

484.12 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

2.2.Кривые второго порядка

1.(x − a)2 + ( y − b)2 = R2 – уравнение окружности с центром в точке C(a, b) и радиуса R.

2.	x2	+	y2	= 1 –	каноническое уравнение эллипса.
2.	a2	+	b2	= 1 –	каноническое уравнение эллипса.
	a2		b2
Фокусы эллипса F (−c;0), F (c;0) , где c =								при a > b ;
Фокусы эллипса F (−c;0), F (c;0) , где c =						a2	− b2	при a > b ;
				1	2

F (0;−c),

F (0;c)

где c =

b2 − a2 , при a < b .

−

= 1,

−

= 1 –

канонические уравнения гипербол, а

F (−c;0),

F (c;0) или F (0; −c), F (0;c)

– их фокусы, где c =

a2 + b2

Прямые y = ±

x –

это асимптоты гиперболы.

4. Канонические уравнения парабол:

y2 = 2 px,

F ( p

;0) –

фокус параболы;

y2 = −2 px,

F (− p

;0) –

фокус параболы;

x2 = 2 py,

F (0; p

) –

фокус параболы;

x2 = −2 py,

F (0;− p

) –

фокус параболы.

2.3.Плоскость

1.Ax + By + Cz + D = 0 – общее уравнение плоскости.

2.Ax + By + Cz + D = 0 – нормальное уравнение плоскости.

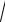± A2 + B2 + C 2

d =

Ax0

+ By0 + Cz0 + D

–

расстояние от точки M

(x0 , y0 , z0 )

до

A2 + B2 + C 2

плоскости

Ax + By + Cz + D = 0.

A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0 – уравнение плоскости, проходящей

через точку M 0 (x0 , y0 , z0 ) и перпендикулярной вектору

= ( A, B,C).

x − x1

5. x2 − x1 x3 − x1

три точки

y − y1	z − z1
y − y1	z − z1
y2 − y1	z2 − z1	= 0 – уравнение плоскости, проходящей через
y3 − y1	z3 − z1

M1 (x1, y1, z1 ), M 2 (x2 , y2 , z2 ), M3 (x3 , y3 , z3 ).

2.4.Прямая в пространстве

1.A1x + B1 y + C1z + D1 = 0, - общее уравнение прямой в пространстве.

A2 x + B2 y + C2 z + D2 = 0

x − x0

y − y0

z − z0

- каноническое уравнение прямой в

пространстве.

x = x0 + lt, y = y0 + mt, z = z0 + nt - параметрические уравнения прямой.

x − x1

y − y1

z − z1

- уравнения прямой, проходящей через точки

x2 − x1

y2 − y1

z2 − z1

M1 и M 2 .

							2.5. Поверхности второго порядка
1.	x2	+	y2	= 1,	x2	−	y2	= 1, y2 = 2 px –	уравнения эллиптического,
	a2		b2		a2		b2

гиперболического и параболического цилиндров.

(x − a)2 + ( y − b)2 + (z − c)2 = R2

– уравнение сферы с центром в точке

C(a,b,c) и радиуса R.

= 1 –

уравнение эллипсоида с центром в точке O( 0,0,0 ).

−

= 0 –

уравнение конуса (конической поверхности).

−

= 1,

−

= −1 –

уравнения

однополостного

двуполостного гиперболоидов.

z =

, z =

−

–

уравнения

эллиптического

гиперболического параболоидов.

3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

		3.1. Функции. Предел и непрерывность
Функция		функция, y0 = f (x0 ) – значение функции в точке x = x0 .
y = f (x)	–	функция, y0 = f (x0 ) – значение функции в точке x = x0 .
y = f (x)	–	явное задание функции; F (x, y) = 0 – неявное задание

некоторой функции y = g(x) ;

x = x(t), y = y(t) – параметрическое задание некоторой функции y = ϕ (x).

Условие непрерывности

Функция y = f (x) непрерывна при значении x = x0 (в точке x = x0 ), если выполняется равенство

lim f (x) = f (x0 )	(1)
x→x0
Если равенство (1) не выполняется, то x0 –	точка разрыва функции.

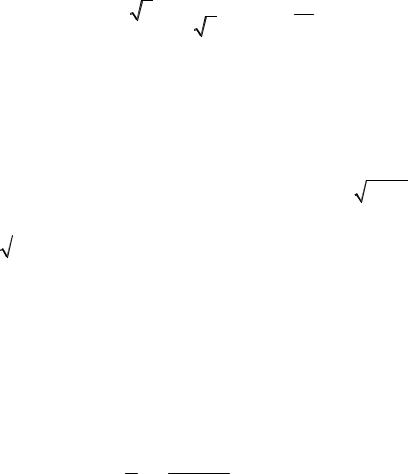
3.2. Производная функции

y = f (x) – функция, x –	приращение независимой переменной x,
y = f (x + x) − f (x) – приращение функции.
y¢ = f ¢(x) = lim	y = lim	f (x +	x) − f (x)
			Dx
x→0	Dx x→0

–производная функции y = f (x) . Производная в точке – это конечный

предел. Если предел (2) бесконечный или не существует, то функция производной в этой точке не имеет.

Операция нахождения производной функции называется дифференцированием.

Если функция разрывна в точке x = x0 , то она не имеет производной в этой точке.

Таблица производных основных элементарных функций

1. (xn )¢ = nxn−1 c¢ =

	1			1	¢
0, x¢ =1, ( x )¢ =
			,
	2

		x x

= - . x2

2.	(ax )¢ = ax ln a					((ex )¢ = ex ).				3. (loga				x)¢ =		1	loga e.
2.	(ax )¢ = ax ln a					((ex )¢ = ex ).				3. (loga				x)¢ =			loga e.
																x
4.	(ln x)¢ =		1	.	5.		(sin x)¢ = cos x.				6.			(cos x)¢ = -sin x.
4.	(ln x)¢ =			.	5.		(sin x)¢ = cos x.				6.			(cos x)¢ = -sin x.
			x							−1
7.	(tgx)¢ =	1			.		8.		(ctgx)¢ =	−1			.		9. (arcsin x)¢ =				1		.
7.	(tgx)¢ =				.		8.		(ctgx)¢ =				.		9. (arcsin x)¢ =						.
		cos2 x								sin2	x							1 - x2
10. (arccos x)¢ =						−1		.	11. (arctgx)¢ =			1			. 12. (arcctgx)¢ =				−1	.
10. (arccos x)¢ =								.	11. (arctgx)¢ =		1 + x2				. 12. (arcctgx)¢ =			1 + x2		.
					1 - x2						1 + x2							1 + x2


	Правила дифференцирования
с –	постоянная (константа),		u = u(x), v = v(x) – функции.
1. c′ = 0.	2. (cu)′ = cu′.	3. (u ± v)′ = u′ ± v′.

4.(u × v)¢ = u¢v + uv¢. 5. ( u )¢ = u¢v - uv¢.

vv2

6.y = F (ϕ (x)) – сложная функция. (F (ϕ (x)))′ = F′(ϕ (x)) ×ϕ′(x).

4. КОМПЛЕКСНЫЕ ЧИСЛА

Действия над комплексными числами: z1 = x1 + y1i, z2 = x2 + y2i.

1.Сложение: z1 + z2 = (x1 + x2 ) + ( y1 + y2 )i.

2.Вычитание: z1 − z2 = (x1 − x2 ) + ( y1 − y2 )i.

3.Умножение:

z × z	2	= (x + y i)(x + y													i) = x x + x y					i + x y i + y y				i2	=
1	2	1				1	2						2		1		2	1	2	2	1	1	2
														= (x1 x2 − y1 y2 ) + (x1 y2 + x2 y1 )i.
Замечание. z ×					= (x + yi)(x - yi) = x2 + y2 .
Замечание. z ×			z		= (x + yi)(x - yi) = x2 + y2 .
					z1		=	z1		×			2		=	(x1 + y1i)(x2 - y2i)					.
4. Деление:					z1			z1		×	z		2			(x1 + y1i)(x2 - y2i)
4. Деление:
				z				z		×							x	2 + y	2
				z		2		z	2	×		z	2				x	2 + y	2
						2			2				2				2	2

Тригонометрическая форма записи.

z = x + yi – алгебраическая форма записи.

z = r(cosϕ + i sinϕ) – тригонометрическая форма, где r = 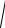x2 + y2 ,

- модуль комплексного числа,					ϕ -			аргумент комплексного числа,
который определяется как				tgϕ = y				x	, ϕ = arctg y	x	.
								x		x
			y	x ,	x > 0
arctg				x ,	x > 0
π + arctg y					x	,		x < 0, y ³ 0
					x

							,		x < 0, y < 0,
ϕ = - π + arctg y						x	,		x < 0, y < 0,
						x
π	2	, x = 0, y > 0
	2
	π	2	,	x = 0, y				< 0
-		2	,	x = 0, y				< 0

Возведение в степень.

n –		натуральное число, z = r(cosϕ + i sinϕ).
zn		= z × z...z (z2 = z × z, z3 = z × z × z).
zn		= [r(cosϕ + i sinϕ)]n = r n (cos nϕ + i sin nϕ) –					формула Муавра.
Извлечение корня.
n		= n		= n		(cos ϕ + 2kπ + i sin ϕ + 2kπ ),
	z		r(cosϕ + i sinϕ)		r
						n	n

где n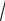r – арифметический корень, k = 0,1,..., n −1. n z имеет n различных значений действительных или комплексных.

	5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Если	F′(x) = f (x) , то F(x)	– первообразная	функции f(x), а
множество	всех первообразных	F (x) + C (где C	– произвольная

постоянная) называют неопределенным интегралом и обозначают

∫ f (x) dx = F (x) + C .

Правила интегрирования

1.∫C f (x) dx = C ∫ f (x) dx .

2.∫ ( f (x) ± g(x)) dx = ∫ f (x) dx ± ∫ g(x) dx .

3. Если ∫ f (x) dx = F (x) + C , то ∫ f (u) du = F (u) + C, где u = ϕ(x) ;

в частности ∫ f (ax + b) dx = 1 F (ax + b) + C. a

Таблица простейших интегралов

1. ∫ x n dx =

x n+1

+ C, n ¹ -1.

n + 1

∫ a x dx =

a x

+ C.

ln a

∫

arctg

+ C.

2 + a 2

∫

x - a

+ C.

2 - a 2

x + a

∫

= ln

x + x 2 + a

+ C.

x 2 + a

10.

∫ sin x dx = - cos x + C.

12.

∫

= tg x + C.

cos2 x

14.

∫

= ln

+ C.

sin x

2.∫ dxx = ln x + C.

4.∫ e x dx = e x + C.

6. ∫

= arcsin

+ C.

2 - x 2

8. ∫

a + x

+ C.

2 - x 2

a - x

11.	∫ cos x dx = sin x + C.
13.	∫	dx		= - ctg x + C.

		sin 2
		sin 2	x
	∫	dx			x		p
15.			= ln		tg	+		+ C.
15.			= ln		tg	+		+ C.
		cos x			2		4

Методы интегрирования

1. Замена переменной.

Если x = ϕ(t) - дифференцируемая функция, то

∫f (x) dx = ∫ f (j(t)) j¢(t) dt + C.

2.Формула интегрирования по частям.

Если u = u(x), v = v(x) - дифференцируемые функции, то

∫u dv = u v - ∫ v du + C.

6.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Формула Ньютона-Лейбница вычисления определенного интеграла

∫ f (x)dx = F (b) − F (a) ,

где F(x) – первообразная функции f(x).

Методы вычисления определенных интегралов

1. Замена переменной.

b	β
∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt,
a	α
где ϕ(α) = a, ϕ(β) = b (при	замене переменной следует пересчитать

пределы интегрирования).

2. Формула интегрирования по частям.

b		b
∫ u dv = u v	b	- ∫ v du.
	b
	a
	a
a		a

3. Формула Ньютона-Лейбница вычисления определенного интеграла

∫ f (x)dx = F (b) − F (a) ,

Площадь криволинейной трапеции.

В декартовых координатах: если фигура ограничена сверху кривой y = f(x) , снизу - кривой y = g(x) , слева и справа - отрезками прямых

		b
x = a и x = b, то её площадь равна:		S = ∫[ f (x) − g(x)] dx .
		a
В полярных координатах: Если фигура ограничена лучами ϕ = α и
			β
ϕ = β и непрерывной кривой ρ = ρ (ϕ) , то			S = 12 ∫ ρ 2 dϕ
			α
Область ограничена кривыми, заданными параметрически. Если
кривая, ограничивающая криволинейную трапецию задана в
параметрическом виде	x = ϕ(t),	, где t1 ≤ t ≤ t2 ,
параметрическом виде		, где t1 ≤ t ≤ t2 ,
	y =ψ (t)

то переход в интеграле к переменной t приводит к формуле

S = ∫ψ (t) ×ϕ¢(t) dt

7. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

z = f (x, y) – функция двух независимых переменных x и y. Область определения функции – это множество точек (x,y) плоскости XOY, в которых функция определена.

7.1. Частные производные

∂z = f	′	(x, y) = lim	f (x +	x, y) − f (x, y)	–
	x
∂x		x→0		x

частная производная функции z по переменной x.

∂z	= f y′(x, y) = lim	f (x, y +	y) − f (x, y)	–
∂y
	y→0		y

частная производная функции z по переменной y.

Все правила дифференцирования остаются справедливыми при нахождении частных производных, только надо помнить, что при

отыскании	∂z	переменная	y	считается	постоянной,	а
	∂x

дифференцирование ведется по переменной х, при отыскании же

∂z переменная x считается постоянной, а дифференцируют – по y.

∂y

z′′

= (z′ )′

z′′

= (z′ )′

z′′

= (z′ )′

z′′

= (z′ )′

–

частные производные

x x

y y

x y

y x

второго порядка.

7.2. Экстремумы функции двух переменных

Функция z = f (x, y) имеет максимум в точке M 0 (x0 , y0 ), если f (M 0 ) > f (M ′) , для любой точки M ′ из окрестности точки M 0 и имеет

минимум в точке M 0 (x0 , y0 ), если	f (M	′	Значения функции в
		0 ) < f (M ).

точках максимума и минимума называют экстремумами функции.

Для определения экстремума сначала находят стационарные точки

(критические). Это точки, в которых частные производные	∂z	,	∂z
	∂x		∂y

равны нулю или не существуют (это необходимые условия экстремума). Если найдена стационарная точка M 0 (x0 , y0 ) , то проверяют

выполнение достаточных условий экстремума. Находят частные

производные второго порядка и вычисляют их значения в стационарной

точке M	0	(x , y ) : A =		f ′′	(x , y ),	B = f ′′	(x , y ),	C = f ′′	(x , y ).
	0	0	0	xx	0 0	xy	0 0	yy		0 0
Если
						= AC − B2 > 0,
то M 0 (x0 , y0 ) –			точка максимума функции при A < 0							(C < 0) ,
или точка минимума при A > 0						(C > 0).
Если = AC − B2 < 0,				то экстремума нет.

8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Уравнение, содержащее производные, называется дифференциальным уравнением.

В общем виде

	′	(1)
	F (x, y, y ) = 0	(1)
–	дифференциальное уравнение 1-го порядка,
	′ ′′	(2)
	F (x, y, y , y ) = 0	(2)
–	дифференциальное уравнение 2-го порядка.
	Функция y =ϕ(x,C), где С –	произвольная постоянная, называется

общим решением уравнения (1), если она удовлетворяет этому уравнению:

F (x, ϕ(x,C), ϕ′(x,C)) = 0, 0 = 0.

Существуют различные типы дифференциальных уравнений и необходимо знать методы их решения. Ниже приводятся некоторые типы дифференциальных уравнений.

8.1. Дифференциальные уравнения с разделяющимися переменными

Если уравнение F (x, y, y′) = 0 можно преобразовать к виду

∫ f ( y)dy = ∫q(x)dx, то оно называется уравнением с разделяющимися

переменными. Общее решение (общий интеграл) находится интегрированием

∫ f ( y)dy = ∫q(x)dx + C.

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.03.2016681.98 Кб252Создание и обработка звука (Павлов).doc
#
08.03.201512.88 Кб24СопроМат правила.docx
#
18.08.201983.46 Кб2Социологическое исследование.doc
#
25.08.201971.68 Кб4Спецификация программных требований.doc
#
27.09.2019160.65 Кб25СПО ЛЕКЦИИ.docx
#
20.03.2016484.12 Кб36справочник математика.pdf
#
08.03.2015115.2 Кб8средства и методы ук.doc
#
23.09.2019149.5 Кб3Стандарт обр по ИЯ.doc
#
08.03.2015243.71 Кб16Стандарт_СТП 1.01-2002.doc
#
08.03.2015203.78 Кб57Стандарт_СТП 1.01-2002.doc
#
08.05.2019243.71 Кб14Стандарт_СТП 1.01-2002.doc