
справочник математика
.pdf
где i-й столбец составлен из координат вектора ai в базисе Е.
T –1 – это матрица перехода от базиса Е к базису А. Матрица перехода от базиса к базису всегда невырождена.
Пусть x1,..., xn – координаты вектора x в базисе Е, y1,..., yn – его координаты в базисе А. Тогда формулы, связывающие столбцы из
координат вектора в разных базисах Е и А соответственно, имеют вид:
X = T Y .
Y= T - 1X .
1.5.Линейные операторы
Линейным оператором в линейном векторном пространстве называется отображение ϕ пространства L в себя (ϕ : L → L) , для
которого выполняются свойства линейности
ϕ(αx ) =αϕ(x ), ϕ(x + y) =ϕ(x ) +ϕ( y ),
где x и y – произвольные элементы из L, α – число.
Линейные операторы можно задавать с помощью матриц. Пусть
ε = ( |
|
|
|
|
|
|
Ln и ϕ – линейный оператор. |
||||
e1, e2 ,..., en ) базис пространства |
|||||||||||
|
ϕ( |
e1 ),ϕ( |
e2 ),...,ϕ( |
|
|
||||||
Разложим образы базисных векторов |
en ) |
||||||||||
ϕ(e1 ) = a11e1 + a21e2 +... + an1en ,
по базису ..................................................
ϕ(en ) = a1ne1 + a2ne2 +... + annen .
Запишем матрицу Aϕ , у которой i-м столбцом будут коэффициенты a1i , a2i ,..., ani разложения вектора ϕ(ei ) :
|
a11 |
a12 ... a1n |
|
||
|
a |
a |
... a |
|
|
A = |
21 |
22 |
2n . |
||
ϕ |
|
...................... |
|||
|
|
|
an 2 |
|
|
|
an1 |
... ann |
|||
Линейному оператору ϕ в базисе e1,..., en однозначно соответствует матрица Aϕ , называемая матрицей линейного оператора.
Обратно, каждой квадратной матрице порядка n соответствует некоторый линейный оператор пространства Ln .
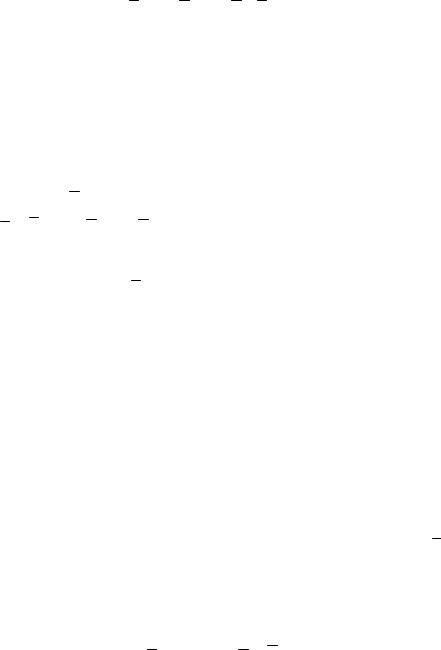
Нетрудно показать, что в разных базисах один и тот же оператор ϕ будет иметь различные матрицы.
Для сокращения будем записывать
(ϕ(e1 )...ϕ(en )) = (e1...en ) Aϕ или ϕ(ε) =εΑϕ .
1.6. Собственные векторы и собственные значения линейного оператора
Пусть ϕ – линейный оператор пространства L.
Вектор x L называется собственным вектором оператора ϕ , если x ¹ 0 и ϕ(x ) = λx.
Число λ называется собственным значением оператора ϕ . Говорят, что вектор x соответствует (принадлежит) собственному значению λ .
Рассмотрим алгоритм нахождения собственных значений и векторов линейного оператора ϕ .
Пусть в пространстве L выбран некоторый базис и
a11 |
a12 |
... a1n |
|
|
x1 |
|
||
|
|
|
... a21 |
|
|
|
|
|
a21 |
a22 |
|
|
x2 |
|
|||
A = |
..................... |
|
, |
X = |
... |
|
||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
an 2 ... ann |
|
|
|
|
|
|
an1 |
|
|
xn |
|
||||
матрица оператора ϕ и координатный столбец вектора x в данном базисе. Тогда можно записать AX = λX или ( A − λE) X = 0. Последнее равенство есть матричное уравнение однородной системы линейных уравнений. Решая эту систему, находят координаты собственного вектора x . Вектор x ¹ 0 , а это возможно только тогда, когда
|
a11 − λ |
a12 |
... |
a1n |
|
|
|
|
|||||
det( A − λE) = |
a21 |
a22 − λ |
... |
a2n |
|
= 0. |
|
............................................... |
|
|
|||
|
an1 |
an 2 |
... |
ann − λ |
|
|
Уравнение называют характеристическим уравнением матрицы А или линейного оператора ϕ . Характеристическое уравнение не зависит
от выбора базиса. Если раскрыть определитель, то получится алгебраическое уравнение n-ой степени с неизвестным λ :
a λn + a |
λn−1 |
+... + a λ + a = 0 |
или |
P (λ) = 0. |
|
n |
n−1 |
1 |
0 |
|
n |
Многочлен Рn (λ) называется характеристическим многочленом
матрицы А или оператора φ. Решая уравнение определяют его корни (собственные значения), а затем последовательно их подставляют в систему уравнений, решениями которой будут собственные векторы, отвечающие собственным значениям.
|
|
|
|
|
|
1.7. Квадратичные формы |
|
|
|
|
|
|
|
||||||||
|
Квадратичной формой q(x1,..., xn ) |
от переменных x1,..., xn |
|
||||||||||||||||||
называется многочлен второй степени |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(x1,..., xn ) = ∑aij xi x j , |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
i, j=1 |
|
|
|
|
|
|
|
|
|
|
|
причем |
aij |
= a ji . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
q(x , x ) = a x 2 |
+ a x x + a x x + a x 2 |
= a x 2 |
+ 2a x x + a x 2 |
||||||||||||||||||
1 |
2 |
11 |
1 |
12 |
1 |
2 |
21 |
2 |
1 |
22 |
2 |
11 |
1 |
|
|
12 |
1 |
2 |
22 |
2 |
|
– общий вид квадратичной формы от двух переменных x1 |
и x2 . |
|
|||||||||||||||||||
|
Квадратичную форму можно записать в матричном виде |
|
|||||||||||||||||||
|
|
|
|
|
|
|
q(x ,..., x ) = X T |
AX , |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
a11 |
|
a12 ... a1n |
|
|
||||||
|
|
X T = (x ...x ), |
X = |
M |
, |
A = ........................ |
. |
|
|||||||||||||
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
a |
n1 |
|
a |
n 2 |
... |
a |
nn |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||
Матрица А называется матрицей квадратичной формы, очевидно,
что она будет симметрической.
Например, матрицей квадратичной формы
q(x1, x2 , x3 ) = x12 + 3x22 − 4x1x2 + 2x2 x3
|
|
1 |
−2 |
0 |
|
|
будет матрица |
A = |
|
−2 |
3 |
1 |
|
|
. |
|||||
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|||

|
|
7 |
−3 |
2 |
|
|
|
Обратно, если известна матрица |
A = |
|
−3 |
4 |
1 |
|
, |
|
|
||||||
|
|
|
2 |
1 |
−5 |
|
|
|
|
|
|
|
|||
то квадратичная форма запишется
q(x1, x2 , x3 ) = 7x12 + 4x22 − 5x32 − 6x1x2 + 4x1x3 + 2x2 x3.
Ранг матрицы А называется рангом квадратичной формы. Если А
– невырожденная матрица, то невырожденной будет и квадратичная форма.
Квадратичная форма называется канонической (имеет
канонический вид), если аij = 0 при i ¹ j .
Матрица канонической квадратичной формы имеет диагональный
вид.
Квадратичная форма q(x1,..., xn ) называется положительно определенной, если q(x1,..., xn ) > 0 для любого ненулевого набора чисел x1,..., xn , и отрицательно определенной, если q(x1,..., xn ) < 0 .
Существует критерий для установления знакоопределенности квадратичной формы - Критерий Сильвестра:
1. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы главные миноры
a11 ... a1k
...................
ak1 ... akk
матрицы А квадратичной формы были положительны для всех k =1,2,..., n .
2. Для отрицательной определенности квадратичной формы необходимо и достаточно, чтобы главные миноры нечетного порядка были отрицательны, а четного – положительны.
1.8. Евклидово пространство
Линейное пространство L называется евклидовым, если в нем определена операция скалярного умножения: каждой паре векторов x и y из L поставлено в соответствие действительное число,
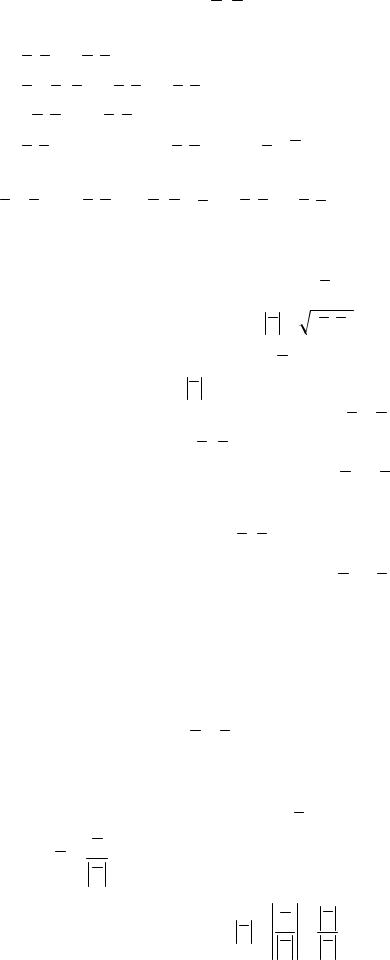
обозначаемое символом (x , y ) , причем, выполнены следующие условия (свойства):
1)(x , y ) = ( y, x ),
2)(x + y, z ) = (x , z ) + ( y, z ),
3) (λx , y ) = λ(x , y ), λ Î R,
4) (x , x ) ³ 0, причем (x , x ) = 0 x = 0.
Из свойств 1−4 следуют свойства:
(x ,λy ) = λ(x , y ), (x , y + z ) = (x , y ) + (x , z ).
Определим некоторые понятия через скалярное произведение. Длина вектора. Длиной вектора x называется число
x = 
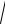 (x , x ).
(x , x ).
Единичный вектор. Вектор e называется единичным или нормированным, если e =1.
Ортогональные векторы. Векторы x и y называются ортогональными, если (x, y) = 0.
Ортогональная система. Система x1,..., xk называется ортогональной, если
(xi , x j ) = 0 при i ¹ j.
Ортонормированный базис. Базис e1,...,en евклидова пространства L называется ортонормированным, если его векторы единичны и попарно ортогональны, т.е.
|
|
|
|
|
1 |
при i = j, |
( |
ei |
, |
e |
j |
) = |
при i ¹ j. |
|
|
|
|
|
0 |
Каждой паре векторов x и y можно произвольным образом поставить в соответствие число, но оно будет скалярным произведением только в том случае, если выполняются свойства 1−4.
Нормирование базиса. Пусть a – произвольный вектор. Тогда вектор e = aa будет нормированным, так как
e = a = a =1. a a
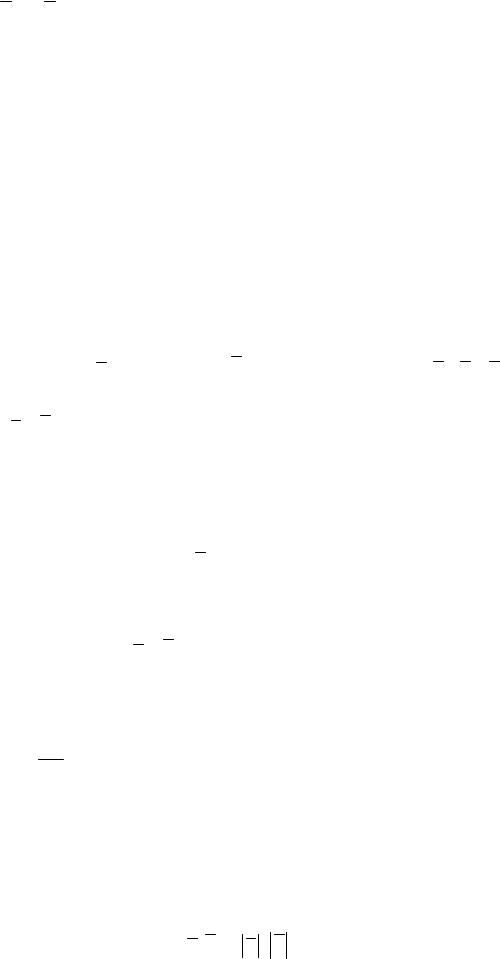
Пусть e1,..., en – ортогональный базис, тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
= |
|
|
|
|
, ..., |
|
′ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
en |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
e |
|
– |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
e1 |
|
n |
en |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ортонормированный базис. В самом деле, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
( |
|
|
|
, |
|
|
|
j ) |
|
0 |
|
|
|
|
|
|
при i ¹ j, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
ei |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(ei¢,ej¢) = |
|
|
|
|
|
|
|
|
|
|
= |
(ei , |
|
ei ) |
=1 |
при i = j. |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
e |
e |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
j |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1.9. Пространство геометрических векторов
Пусть даны a = (x1, y1 , z1 ) и b = (x2 , y2 , z2 ) в базисе e1, e2 , e3 . Тогда справедливы утверждения:
1. Если a = b , то
x1 = x2 , y1 = y2 , z1 = z2 .
2.При умножении вектора на число каждая его координата умножается на это число
λa = (λx1, λy1, λz1 ).
3.При сложении (вычитании) векторов складываются (вычитаются) их соответствующие координаты
a ± b = (x1 ± x2 , y1 ± y2 , z1 ± z2 ).
4. Еслиa // b , то |
x2 |
= |
y2 |
= |
z2 |
. |
x1 |
y1 |
|
||||
|
|
|
z1 |
|||
5. Координаты вектора: даны точки A(x1, y1, z1 ) и B(x2 , y2 , z2 )
AB = (x2 − x1 ; y2 − y1 ; z2 − z1 ) .
1.9.1.Скалярное произведение
Впространстве V3 скалярное произведение задается по правилу
(a ,b ) = a × b × cosϕ,

где ϕ – угол между векторами a и b (0 ≤ϕ ≤π) . Из следует, что (a,b ) = 0 , если a = 0 или b = 0 , или a b .
Пусть даны a = (x1, y1, z1 ) , b = (x2 , y2 , z2 ) в ортонормированном базисе i , j , k . Тогда
(a,b ) = x1x2 + y1 y2 + z1z2 .
Приложения
1.Длина вектора (a, a ) = a 2 и a = 
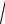 (a , a ).
(a , a ).
Для вектора a = (x1, y1, z1 ) получим
a= 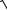
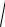 x12 + y12 + z12 .
x12 + y12 + z12 .
2.Расстояние между точками. Если даны точки A(x1, y1, z1 ) и
B(x2 , y2 , z2 ) , то расстояние между ними равно длине вектора AB
AB = 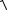
 (x2 - x1 )2 + ( y2 - y1 )2 + (z2 - z1 )2 .
(x2 - x1 )2 + ( y2 - y1 )2 + (z2 - z1 )2 .
3. |
Условие ортогональности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
x1x2 + y1 y2 + z1z2 = 0. |
|
|
|
||||||||||||||||||||||||||||||||||||||||
4. |
Угол между векторами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
, |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x2 + y1 y2 |
+ z1z2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
cosϕ = |
a |
= |
|
. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
x12 + y12 + z12 × |
x22 + y22 + z22 |
|
|
|||||||||||||||||||||||
5. |
Проекция вектора на вектор и на оси координат. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
( |
|
|
|
, |
|
|
) |
= |
x1 |
x2 + y1 y2 + z1z2 |
. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
np |
|
|
|
a |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
x22 + y22 + z22 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Проекции вектора |
|
на координатные оси Ox,Oy,Oz . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
( |
|
|
|
, |
|
|
) |
. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
np |
|
|
|
= np |
|
|
|
|
a |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
a |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ox |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Координаты вектора в ортонормированном базисе численно равны проекциям вектора на оси координат:
x1 = npox a , y1 = npoy a, z1 = npoz a ,

6. Направляющие косинусы вектора. Пусть α , β ,γ – углы,
образованные вектором a = (x, y, z) соответственно с осями координат
Ox,Oy,Oz .
cosα = |
|
x |
|
, |
cos β = |
|
y |
|
, |
cosγ = |
|
z |
|
. |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
cos2 α + cos2 β + cos2 γ =1 и e = (cosα ,cos β ,cosγ )
– единичный вектор.
7. Деление отрезка в данном отношении. Пусть даны точки
M1 (x1, y1, z1 ), M 2 (x2 , y2 , z2 ) и отношение λ ¹ -1, в котором точка M ( x, y, z ) делит направленный отрезок M1M 2 . Тогда координаты точки М определяются как:
x = |
x1 + λ x2 |
, y = |
y1 + λ y2 |
, z = |
z1 + λ z2 |
. |
1 + λ |
1 + λ |
|
||||
|
|
|
1 + λ |
|||
Замечание. Число λ может быть отрицательным, если точка М находится вне отрезка M1M 2 , и λ = 0 , если М совпадает с M1 .
8. Работа постоянной силы. Рассмотрим задачу. Под действием постоянной силы F некоторая материальная точка перемещается прямолинейно из положения В в положение С. Работа силы F , при перемещении из В в С, определяется как
A = F × BC cosϕ или A = (F , BC).
1.9.2. Векторное произведение
Векторным произведением вектора a на вектор b называется вектор, обозначаемый символом [a,b ] (или a ´ b ), определяемый тремя условиями:
1) [a ,b ] = a × b sinϕ, где ϕ - угол между a и b ;
2)вектор [a,b ] перпендикулярен векторам a и b ;
3)упорядоченная тройка векторов a,b ,[a,b ] – правая
Очевидно что [i , i ] = [ j , j ] = [k , k ] = 0;

[i , j ] = k , [ j , k ] = i , [k , i ] = j .
В ортонормированном базисе |
|
|
|
|
векторное произведение [ |
|
, |
b |
] |
||||||||||||||||||
a |
|||||||||||||||||||||||||||
определяется как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
i |
|
|
|
j |
|
|
|
|
|
|
k |
|
|
|
|
|
|||||
[ |
|
, |
|
] = |
x1 |
y1 |
|
|
|
z1 |
, |
|
|
|
|||||||||||||
|
b |
||||||||||||||||||||||||||
a |
|||||||||||||||||||||||||||
|
|
|
|
|
x2 |
y2 |
|
|
z2 |
|
|
|
|
||||||||||||||
Приложения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Площадь параллелограмма вычисляется по формуле |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
× |
|
|
|
×sinϕ. |
||||||||||||||
|
|
|
SABCD = |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
AB |
AC |
|||||||||||||||||||||||
Площадь треугольника АВС равна
SABC = 12 [ AB, AC] .
1.9.3. Смешанное произведение
Смешанным произведением упорядоченной тройки векторов a,b ,c называется число ([a ,b ],c ) . Здесь вектор a умножается векторно на b , в результате чего получится некоторый вектор, который скалярно умножится на вектор c .
Нетрудно показать, что ([ |
|
|
|
, |
|
|
], |
|
|
|
) > 0 , если тройка |
|
, |
|
, |
|
правая, и |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
c |
a |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
([ |
|
, |
|
], |
|
) < 0 , если тройка |
|
|
, |
|
, |
|
|
|
|
– левая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
a |
c |
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
Если |
|
= (x1, y1, z1 ), |
|
|
|
|
|
= (x2 , y2 , z2 ), |
|
|
= (x3 , y3 , z3 ) |
в ортонормированном |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
базисе, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ([ |
|
|
|
, |
|
], |
|
) = |
|
x1 |
y1 |
z1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
abc |
|
|
|
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
y3 |
|
z3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приложения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1. Компланарность векторов. Если |
|
|
|
|
|
= 0 , |
|
|
то |
векторы |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
,b , |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
abc |
|
|
|
a |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
компланарны, иначе они не компланарны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2. Объем тетраэдра. Рассмотрим тетраэдр (пирамида, основание которой есть треугольник ABD) с вершинами в точках A, B, D, A′ . Известно, что объем этого тетраэдра составляет шестую часть объема параллелепипеда, построенного на векторах a,b ,c . Следовательно,
Vтет = 16 abc .
2.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
2.1.Прямая линия на плоскости
1.Ax + By + C = 0 – общее уравнение прямой на плоскости.
2. |
|
|
Ax |
+ By + C |
= 0 – |
|
|
|
нормальное уравнение прямой. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
A2 + B2 |
||||||||||||||||||||||||
|
± |
|
|
|
|
|
|
|
|
|||||||||||||||
Здесь |
|
μ = |
|
|
|
1 |
|
|
|
|
|
- |
нормирующий множитель, знак берется |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
± |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
А2 + В2 |
||||||||||||||||||||||
противоположным знаку свободного члена. |
||||||||||||||||||||||||
3. |
d = |
|
|
Ax0 + By0 + C |
|
|
|
– |
расстояние от точки M 0 (x0 , y0 ) до прямой |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
A2 + B2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ax + By + C = 0. |
|
|
|
|
|
|||||||||||||||||||
4. |
|
|
x − x0 |
= |
|
y − y0 |
|
– |
|
каноническое уравнение прямой. |
||||||||||||||
|
|
|
l |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|||||||||||
5. |
|
x = lt + x0 |
, y = mt + y0 |
– параметрические уравнения прямой. |
||||||||||||||||||||
6. |
|
|
x − x1 |
|
= |
y − y1 |
– |
|
|
|
уравнение прямой, проходящей через точки |
|||||||||||||
|
x2 − x1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
y2 − y1 |
|
|
|
|
|
|||||||||||||
M1 (x1, y1 ), M 2 (x2 , y2 ).
