k_Fomin

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тамбовский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Тогда систему (2) можно записать в матричной форме:

.pdf

Скачиваний:

Добавлен:

20.03.2016

Размер:

1.26 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

В.И. ФОМИН

МАТЕМАТИКА 1.1

• ИЗДАТЕЛЬСТВО ТГТУ •

УДК 51(075)

ББК В11я73

Ф753

Р е ц е н з е н т ы:

Доктор физико-математических наук, профессор, заведующий кафедрой алгебры и геометрии ТГУ им. Г.Р. Державина

А.И. Булгаков

Доктор физико-математических наук, профессор, заведующий кафедрой прикладной математики и механики ТГТУ

Г.М. Куликов

Фомин, В.И.

Ф753 Математика 1.1 : учебное пособие для студентов заочной и дистанционной форм обучения / В.И. Фомин. – Тамбов : Изд-во Тамб. гос. техн. ун-та, 2007. – 100 с. – 200 экз. – ISBN 5-8265-0605-9 (978-5-8265-0605-9).

Содержит справочный материал по различным разделам математики, необходимый для выполнения трех контрольных работ, предусмотренных Государственным образовательным стандартом высшего профессионального образования. Рассмотрены методы решения типовых задач, входящих в контрольные работы.

Предназначено для студентов заочной и дистанционной форм обучения первого курса инженерных специальностей вузов.

УДК 51(075)

ББК В11я73

ISBN 5-8265-0605-9	ГОУ ВПО "Тамбовский государственный
(978-5-8265-0605-9)	технический университет" (ТГТУ), 2007

Министерство образования и науки Российской Федерации

ГОУ ВПО "ТАМБОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

В.И. Фомин

МАТЕМАТИКА 1.1

Утверждено Ученым советом университета в качестве учебного пособия для студентов заочной и дистанционной форм обучения

Тамбов

Издательство ТГТУ

2007

Учебное издание

ФОМИН Василий Ильич

МАТЕМАТИКА 1.1

Учебное пособие

Редактор З.Г. Чернова Инженер по компьютерному макетированию М.Н. Рыжкова

Подписано в печать 13.06.2007 Формат 60 × 84/16. 5,81 усл. печ. л. Тираж 200 экз. Заказ № 363

Издательско-полиграфический центр Тамбовского государственного технического университета

392000, ТАМБОВ, СОВЕТСКАЯ, 106, К. 14

ВВЕДЕНИЕ

Цель данного учебного пособия – помочь студентам первого курса заочной и дистанционной форм обучения инженерных специальностей вузов самостоятельно выполнить три контрольные работы по различным разделам математики, предусмотренным Государственным образовательным стандартом высшего профессионального образования (тексты контрольных заданий см. в пособии: Фомин В.И. Математика. Контрольные задания. – Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. – 88 с.; Электронный вариант: Электронная библиотека системы федеральных образовательных порталов: http: window.edu.ru/window/library: Фомин В.И. Математика. Контрольные задания. – Тамбов: Изд-во ТГТУ, 2004.)

Необходимый справочный материал снабжен двойной нумерацией: первый номер – это номер контрольной работы, второй номер – это номер задачи из соответствующей контрольной работы, к которым относится данный материал.

Типовые задачи, решение которых изложено в учебном пособии, снабжены аналогичной двойной нумерацией.

:: =

ДПСК

↑↑

↑↓

ir, rj, kr

rr ab r r a ×b rrr abc

Oδ (x0 )

O&δ (x0 )

R D( y)

Pn (x) A B A B

f (x0 +0)

f (x0 −0)

или

lim f (x)

x→x0

f ′(x0 )

ОБОЗНАЧЕНИЯ

–оператор определения («это по определению»)

–пустое множество

–декартова прямоугольная система координат

–сонаправленность

–противоположная направленность

–параллельность, коллинеарность

–непараллельность, неколлинеарность

–перпендикулярность, ортогональность

–неперпендикулярность, неортогональность

–нулевой вектор

–единичные векторы координатных осей

–модуль (длина) вектора ar

–скалярное произведение векторов ar и b

–векторное произведение векторов ar и b

–смешанное произведение векторов ar , b , cr

–дельта-окрестность точки x0

–проколотая дельта-окрестность точки x0

–квантор общности («для любого», «для каждого», «для всякого»)

–квантор существования («существует», «найдется»)

–«такой (такая, такое), что»

–множество действительных чисел

–область определения функции y

–многочлен степени n переменной x

– множество A включено во множество B и A ≠ B

–множество A включено во множество B (возможно, что A = B )

–правосторонний предел функции f (x) в точке x0

–левосторонний предел функции f (x) в точке x0

–знакравносильности(эквивалентности) («тогдаитолькотогда»)

–конъюнкция («и»)

–знак принадлежности («принадлежит»)

–знак непринадлежности («не принадлежит»)

–предел функции f (x) в точке x0 (при x → x0 )

–производная функции f (x) в точке x0

:: = матрица вида

Контрольная работа 1

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

1.1. МАТРИЦЫ, ДЕЙСТВИЯ НАД НИМИ

Матрица размеров m×n :: = массив m n чисел aij (1 ≤ i ≤ m , 1 ≤ j ≤ n ), расположенных в виде таблицы, состоящей из m горизонтальных и n вертикальных рядов:

a11

a21

Α = Kai1

Kam1

a	K a	K a
12	1 j	1n
a22	K a2 j	K a2n
K	K K	K K	,
ai2	K aij	K ain
ai2	K aij	K ain
K	K K	K K
a	K amj	K a
m2		mn

при этом числа aij называются элементами матрицы, горизонтальные ряды – строками матрицы, вертикальные ряды –

столбцами матрицы.

Таким образом, матрица размеров m×n имеет m строк и n столбцов; первый индекс элемента aij указывает на номер

строки, второй – на номер столбца, на пересечении которых стоит этот элемент. Сокращенное обозначение матрицы разме-

ров m×n : Α = (aij )m,n .

Транспонированная матрица к матрице Α = (aij )m,n

a11

ΑΤ = a12Ka1n

a	K a
a21	K am1
22	m2	.
K	K K	.
K	K K
a2n
a2n	K amn

Операция перехода от матрицы Α к матрицеΑΤ называется транспонированием матрицы А.

Прямоугольная матрица размеров m×n :: = матрица Α = (aij )m,n , для которой m ≠ n . Квадратная матрица порядка n :: = матрица Α = (aij )m,n , для которой m = n :

	a11		a12	K a1n
	a		a	K a
Α =		21	22	2n	.
Α =		K	K	K K	.
		K	K	K K
			an2
	an1		an2	K ann

Сокращенное обозначение квадратной матрицы порядка n: Α = (aij )n .

Главная диагональ квадратной матрицы порядка n :: =ее диагональ, идущая от левого верхнего угла к правому нижнему углу, т.е. диагональ, составленная из элементов a11, a22 ,K, ann .

Побочная диагональ квадратной матрицы порядка n :: = ее диагональ, идущая от правого верхнего угла к левому нижнему углу, т.е. диагональ, составленная из элементов a1n ,K, an1 .

Верхняя треугольная матрица порядка n :: = матрица Α = (aij )n , для которой aij = 0 для 1 ≤ i , j ≤ n , таких что i > j :

a11 a12			a13	K a1n
	0	a	a	K a
		22	23	2n
Α =	0	0	a	K a .
			33	3n
	K	K	K	K K
	0	0	0	K a
				nn

Нижняя треугольная матрица порядка n :: = матрица Α = (aij )n , для которой aij = 0 для 1 ≤ i , j ≤ n , таких что i < j :

a11		0	0	K	0
a		a	0	K	0
	21	22
Α = a		a	a	K	0	.
	31	32	33
	K	K	K	K K
a		a	a	K	a
	n1	n2	n3		nn

Треугольная матрица порядка n :: = верхняя треугольная или нижняя треугольная матрица порядка n.

Диагональная матрица порядка n :: = матрица Α = (aij )n , для которой aij = 0 для 1 ≤ i , j ≤ n , i ≠ j :

a11			0	0	K		0
	0		a	0	K		0
			22
Α =	0		0	a	K		0	.
				33
	K		K	K	K K
	K		K	K	K K
	0		0	0	K	a
							nn
Единичная матрица порядка n :: = матрица Α = (aij )n , для которой								aii =1 для 1 ≤ i ≤ n и aij = 0 для 1 ≤ i , j ≤ n ,
i ≠ j :
	1		0	0	K	0
		0	1	0	K 0
		0	1	0	K 0
Ε =		0	0	1	K	0	.

	K K			K K K
		0	0	0	K 1
		0	0	0	K 1

Таким образом, единичная матрица – это частный случай диагональной матрицы.

Нулевая матрица размеров m×n :: = матрица Α = (aij )m,n , для которой aij = 0 для 1 ≤ i ≤ m ,1 ≤ j ≤ n :

0		0	0	K 0
	0	0	0	K 0

Οm,n =	0	0	0	K 0	.

K		K K K K
	0	0	0	K 0

Нулевую матрицу порядка n принято обозначать Οn .

Ненулевая матрица размеров m × n :: =матрица Α = (aij )m,n , у которой хотя бы один элемент отличен от нуля.

Матрица-строка длины n :: = матрица Α = (a1 j )1,n = (a11

a12 a1n ) .

a11

Матрица-столбец высоты m :: =матрицаΑ =

)

m,1

Пусть Α = (aij )

, Β = (bij )

am1

. Тогда Α = Β , если aij = bij

для 1 ≤ i ≤ m ,1 ≤ j ≤ n ;

m,n

Α+Β ::=

C = (cij )m,n , где cij

= aij +bij

для 1 ≤ i ≤ m ,1 ≤ j ≤ n

( Α +Β − сумма матриц Α и Β);

Α −Β ::=

C = (cij )m,n , где cij

= aij −bij

для 1 ≤ i ≤ m ,1 ≤ j ≤ n

( Α −Β − разность матриц Α и Β);

αΑ ::= C = (cij )m,n , где cij

= αaij для 1 ≤ i ≤ m ,1 ≤ j ≤ n

(здесь α − любое действительное число) ( αΑ− произведение

матрицы Α на числоα ).

Пусть Α = (aij )

, Β = (bij )

n,l

. Тогда ΑB ::= C = (cij )m,l , где cij

= ai1b1 j + ai2b2 j +K+ ainbnj для 1 ≤ i ≤ m ,1 ≤ j ≤ l ( ΑB

m,n

– произведение матрицы Α на матрицу B ).

Задача

1.1. Даны две матрицы Α и B . Найти ΑB , BA . Проверить выполнимость равенства ΑB = BA .

7 5 1

−2

;

Β =

Α =

5 3 −1 .

−5

1 2 3

Решение.

	c11	c12	c13
=	c	c	c	,
	21	22	23
	c	c	c
	31	32	33

c11 =1 7 + 2 5 +1 1 =18,			c12 =1 5 + 2 3 +1 2 =13,
c13 =1 1+ 2 (−1) +1 3 = 2;
c21 =1 7 +(−2) 5 + 4 1 =1,			c22 =1 5 + (−2) 3 + 4 2 = 7,
c23 =1 1+(−2) (−1) + 4 3 =15;
c31 = 3 7 +(−5) 5 +3 1 = −1,			c32 = 3 5 +(−5) 3 +3 2 = 6,
c33 = 3 1+(−5) (−1) +3 3 =17;
	18		13	2
		1	7	15
	ΑΒ =	1	7	15	.
		−1	6	17
		−1	6	17
					d	d	d
					d	d	d
					11	12	13
				= d21		d22	d23 ,
						d32
					d31	d32	d33

d11 = 7 1+5 1+1 3 =15,

d12 = 7 2 +5 (−2) +1 (−5) = −1,

d13 = 7 1+5 4 +1 3 = 30;

d21 = 5 1+3 1+(−1) 3 = 5,

d22 = 5 2 +3 (−2) + (−1) (−5) = 9,

d23 = 5 1+3 4 +(−1) 3 =14;

d31 =1 1+ 2 1+3 3 =12,

d32 =1 2 + 2 (−2) +3 (−5) = −17,

d33 =1 1+ 2 4 +3 3 =18;

−1

ΒΑ =

−17

Так как c11 ≠ d11

(18 ≠15 ), то ΑΒ ≠ ΒΑ .

Задача 1.1 решена.

1.2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Система m линейных уравнений с n неизвестными :: = система вида

a x

+ a x

+K+ a x

= b ;

11 1

1n n

a21x1 + a22 x2 +K+ a2n xn

= b2 ;

(1)

LLLLLLLLLLL

+ a x

+K+ a

= b ,

m1 1

mn n

где x1 , x2 ,K, xn

– неизвестные величины; aij (1 ≤ i ≤ m ,

1 ≤ j ≤ n ) – некоторые заданные числа, называемые коэффициен-

тами системы (1); bi (1 ≤ i ≤ m ) – некоторые заданные числа, называемые свободными членами системы (1); при этом, если

все свободные члены равны нулю, то система (1) называется однородной; если хотя бы один из свободных членов отличен от нуля, то система (1) называется неоднородной.

Решение системы (1) :: = упорядоченный набор чисел ( ξ1 , ξ2 ,K, ξn ), при подстановке которых в уравнения системы

(1) соответственно вместо x1 , x2 ,K, xn получаются верные числовые равенства, при этом числа ξi (1 ≤ i ≤ n ) называются компонентами данного решения. Решение ( ξ1 , ξ2 ,K, ξn ) системы (1) можно записывать в виде x1 = ξ1 , x2 = ξ2 ,K, xn = ξn .

Пусть М – множество решений системы (1).

Система (1) называется несовместной, если она не имеет решений, т.е. если M = . Система (1) называется совместной, если она имеет хотя бы одно решение, т.е. если M ≠ . Совместная система (1) называется определенной, если она имеет единственное решение. Совместная система (1) называется неопределенной, если она имеет более, чем одно решение.

Матрица (основная матрица) системы (1) :: = матрица Α = (aij )m,n , составленная из коэффициентов системы (1):

	a11		a12
	a		a
Α =		21	22
Α =		K	K
		K	K
			am2
	am1		am2

Ka1n

Ka2n .

Kamn

Расширенная матрица системы (1) :: = матрица, получаемая из основной матрицы А системы (1) добавлением к ней столбца свободных членов:

a11

a12

K a1n

K a

Α =

K K

K .

am1

am2 K amn

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

a x + a x + a x = b ;

a21x1 + a22 x2 + a23 x3 = b2 ;

(2)

a x + a x + a x = b .

Матрица системы (2) имеет вид

a11

a12

a13

Α = a

(3)

Определитель (детерминант) системы (2) (или матрицы (3)) :: = число, записываемое в виде

a11

a12

a13

∆ =

a21

a22

a23

(4)

a31

a32

a33

и вычисляемое по формуле

a11	a12	a13
a21	a22	a23	= a11a22a33 + a12a23a31 + a21a32a13 −
a31	a32	a33
			−a13a22a31 −a12a21a33 −a23a32a11 .	(5)

При этом числа aij (1 ≤ i, j ≤ 3 ) называются элементами определителя; горизонтальные ряды этих чисел – строками определителя; вертикальные ряды – столбцами определителя; диагональ, составленная из элементов a11 , a22 , a33 , − главной диагональю определителя; диагональ, составленная из элементов a13 , a22 , a31 , − побочной диагональю определителя; слагаемые в

правой части формулы (5) − членами определителя.

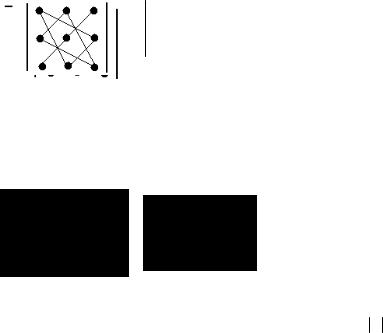
Для записи формулы (5) удобно использовать следующую схему:

(6)

где слева схематически указанно правило записи членов определителя со знаком «+», а справа – правило записи членов определителя со знаком «−».

Определитель ∆ матрицы А принято также обозначать через det Α или Α .

Определитель (4) называется определителем третьего порядка.

Вспомогательные определители системы (2)

:: = определители, получаемые из определителя ∆ системы (2) заменой в

нем одного из столбцов столбцом свободных членов:

a12

a13

a11

a13

a11

a12

∆1 =

a22

a23

; ∆2 =

a21

a23

; ∆3 =

a21

a22

a32

a33

a31

a33

a31

a32

Правило Крамера (Крамер Г. (1704 − 1752) – швейцарский математик): если ∆ ≠ 0 , то система (2) имеет единственное решение, которое находится по формулам

x	=	∆1	;	x	=	∆2	;	x	=	∆3 .	(7)
1		∆		2		∆		3		∆

Формулы (7) называются формулами Крамера.

Укажем матричный способ решения системы (2). Наряду с матрицей А системы (2) введем в рассмотрение матрицы – столбцы неизвестных и свободных членов:

ΑX = B .

(8)

Определитель второго порядка :: = число, записываемое в виде

∆= µ11 µ12

µ21 µ22

и вычисляемое по формуле

∆ =	µ11	µ12	= µ µ	22	−µ µ	21	.

	µ21	µ22	11		12

Минор Μij элемента aij матрицы (3) :: =определитель второго порядка, составленный из элементов матрицы (3), ос-

тающихся после вычеркивания ее i-й строки и j-го столбца.
Например, минор элемента a32		имеет вид
			M32	=	a11	a13	.
			M32	=	a11	a13	.
					a21	a23
Алгебраическое дополнение Α	ij	элемента a	матрицы (3) :: = минор M					ij	этого элемента, взятый со знаком (−1)i+ j :
	ij	ij						ij

Αij = (−1)i+ j Mij .

Например, алгебраическое дополнение элемента a12 имеет вид

Α12 = (−1)1+2 a21 a23 . a31 a33

Заметим, что если сумма i + j четна, то алгебраическое дополнение элемента aij совпадает с его минором, если i + j нечетна, то алгебраическое дополнение элемента aij отличается от его минора лишь знаком.

Матрица (3) называется невырожденной (или неособенной), если ее определитель ∆ отличен от нуля. Матрица (3) называется вырожденной (или особенной), если ∆ = 0 .

Обратная матрица к матрице (3) :: = матрица Α−1 | ΑΑ−1 = Ε, Α−1Α = Ε , где Е – единичная матрица.

Если матрица (3) является невырожденной, т.е. ∆ ≠ 0 , то для нее существует обратная матрица Α−1 и Α−1 находится по формуле

		Α11		Α21		Α31
Α−1 =	1		Α	Α		Α		,	(9)
					22		32
			12
	∆		Α	Α	23	Α	33
			13

где Αij −алгебраические дополненияэлементов aij (1 ≤ i, j ≤ 3 ) матрицы(3).

Заметим, что алгебраические дополнения к элементам первой строки матрицы (3) записываются в первый столбец матрицы в формуле (9), второй строки – во второй столбец, третьей строки − в третий столбец.

Пусть матрица (3) является невырожденной. Тогда существует обратная матрица Α−1 . Умножая обе части (8) слева на матрицу Α−1 , получаем

Α−1(ΑX) = Α−1Β.	(10)
В силу свойства ассоциативности
Α−1(ΑX) = (Α−1Α)X .	(11)

Заметим, что

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.05.20151.09 Mб40kursovaya.rtf
#
21.11.20186.65 Mб3kursovaya_-_2913 (2).doc
#
20.03.201676.49 Кб10Kursovaya_bts-31.docx-10938624.docx
#
20.03.2016689.43 Кб96kursovaya_rabota.docx
#
14.09.2019113.96 Кб5kursovik.docx
#
20.03.20161.26 Mб13k_Fomin.pdf
#
22.05.2015317.42 Кб12k_Glazkov1.pdf
#
22.05.2015691.24 Кб21k_Jukov.pdf
#
22.05.201570.4 Кб14K_r_Skrebnev.docx
#
22.05.2015336.38 Кб16lab_aKiTp.doc
#
22.05.201542.59 Mб54Language_Leader_Intermediate_WB.pdf