
k_Fomin
.pdf
Α−1Α = Ε, ΕX=X. |
(12) |
В силу (10) − (12) |
|
X=Α−1B . |
(13) |
Итак, при матричном способе решения матрица-столбец неизвестных находится по формуле (13). |
|
Систему (2) можно решить также методом Гаусса (методом последовательного исключения неизвестных) (Гаусс К.Ф (1777 − 1855) – немецкий математик, астроном, физик и геодезист).
Пусть a11 ≠ 0 (если a11 = 0 , то в системе (2) надо первое уравнение поменять местами с каким-либо другим уравнением, у которого коэффициент при неизвестной x1 отличен от нуля, и в дальнейшем рассматривать вновь полученную систему
уравнений, которая равносильна (эквивалентна) исходной системе (2) (две системы линейных уравнений называются равносильными, если множества их решений совпадают)). Преобразуем систему (2), исключая неизвестное x1 из второго и третье-
го уравнений. Для этого обе части первого уравнения, умноженные на число a21 , вычтем из соответствующих частей второ-
a11
го уравнения; затем обе части первого уравнения, умноженные на число a31 , вычтем из соответствующих частей третьего
a11
уравнения. В результате придем к системе вида
a |
x + a |
x |
+ a |
x |
= b ; |
(14.1) |
|
|||
|
11 |
1 |
12 |
2 |
13 |
3 |
1 |
|
|
|
|
|
|
′ |
|
′ |
|
′ |
; |
(14.2) |
(14) |
|
|
a22 x2 |
+ a23 x3 |
= b2 |
||||||
|
|
|
a′ |
x |
+ a′ |
x |
= b′ . |
(14.3) |
|
|
|
|
|
32 |
2 |
33 |
3 |
3 |
|
|
|
Полученная система уравнений (14) равносильна исходной системе (2).
Может оказаться, что хотя бы в одном из двух последних уравнений системы (14) коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля. Пусть, например, уравнение (14.2) имеет вид 0 x2 +0 x3 = b2 , где b2 ≠ 0 . В
этом случае система (14) несовместна и, следовательно, равносильная ей исходная система (2) тоже несовместна. Возможен случай, когда в одном из двух последних уравнений системы (14) коэффициенты при неизвестных и свобод-
ный член равны нулю. Пусть, например, уравнение (14.2) имеет вид
0 x2 +0 x3 = 0 . |
(15) |
Уравнение (15) удовлетворяется при любых значениях неизвестных x2 , x3 , поэтому его можно отбросить и перейти от системы (14) к равносильной ей системе
|
|
|
a x + a x + a x = b ; |
|
(16) |
||||||||
|
|
|
|
11 |
1 |
12 |
2 |
13 |
3 |
1 |
|
||
|
|
|
|
|
|
′ |
|
′ |
|
′ |
|
|
|
′ |
|
|
|
|
a32 x2 |
+ a33 x3 = b3 . |
|
|
|||||
|
o |
|
|
|
|
|
|
|
|
|
|
||
Если a33 = |
0 , то из второго уравнения системы (16) находим |
и подставляем найденное значение в первое урав- |
|||||||||||
x2 = x2 |
|||||||||||||
нение |
системы |
|
|
|
|
|
|
|
|
|
|
(16). |
|
В результате получаем уравнение вида |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a11x1 + a13 x3 = b1′ . |
|
|
|
(17) |
|||||
Полагая x3 |
равным произвольному числу γ (γ R) и подставляя в уравнение (17) вместо x3 |
параметр γ |
, находим из |
||||||||||
полученного уравнения x1 = ϕ(γ) . Тогда множество решений системы (16) и, тем самым, системы (2) в случае |
′ |
имеет |
|||||||||||
a33 = 0 |
|||||||||||||
вид
M ={(ϕ(γ) , x2o , γ)| γ R},
т.е. система (2) имеет бесконечное множество решений. Если положить γ , равным конкретному числу γ , то получим кон-
кретное решение |
(ϕ(γ |
* |
) , xo |
, γ |
* |
) . |
|
|
2 |
|
|
||
′ |
, то полагая x3 = γ (γ R) и подставляя во второе уравнение системы (16) вместо x3 параметр γ , находим |
|||||
Если a33 ≠ 0 |
||||||
из полученного уравнения |
x2 = ψ(γ) . Затем в первое уравнение системы (16) вместо x2 и x3 подставляем соответственно |
|||||
ψ(γ) и γ и из полученного уравнения находим x1 = ϕ(γ) . Тогда множество решений системы (16) и, тем самым, системы (2) в случае a33′ ≠ 0 имеет вид
M ={(ϕ(γ) , ψ(γ) , γ)| γ R},
т.е. система (2) является неопределенной.
Если второе и третье уравнения системы (14) имеют вид (15), то отбрасывая их, переходим от системы (14) к равносильному ей уравнению
a11x1 + a12 x2 + a13 x3 = b1 . |
(18) |
Полагая x3 = γ , x2 = β |
и подставляя в уравнение (18) вместо x2 и x3 соответственно β |
и γ , находим из полученного |
|||||||||
уравнения x1 = ϕ(β, γ) . Тогда множество решений уравнения (18) и, тем самым, системы (2) имеет вид |
|
|
|||||||||
|
|
|
M = |
{( |
ϕ(β, γ) , |
β, γ |
) |
} |
|
|
|
|
|
|
|
|
| β, γ R , |
|
|
|
|||
т.е. система (2) имеет бесконечное множество решений. |
|
|
|
|
|
|
|||||
Если положить β |
и γ |
равными конкретным числам β* и γ* , то получим конкретное решение (ϕ(β* , γ* ) , β* , γ* ) . |
|
|
|||||||
|
|
|
′ |
′ |
|
|
|
|
o |
|
|
Вернемся к системе (14). Пусть a22 ≠ 0 (если a22 = 0 , то из уравнения (14.2) найдем |
x3 = x3 ; подставив в уравнение |
||||||||||
(14.3) вместо x число |
xo |
, найдем из полученного уравнения x |
|
= xo ; затем, подставив в уравнение (14.1) вместо x |
и x |
||||||
3 |
|
3 |
|
|
|
2 |
2 |
2 |
|
3 |
|
соответственно xo |
и xo |
, найдем из полученного уравнения x |
= xo |
). Преобразуем систему (14), исключая неизвестное x |
|
из |
|||||
2 |
3 |
|
|
|
1 |
1 |
|
2 |
|
||
|
|
|
|
′ |
|
|
|
|
|
|
|
|
третьего уравнения. Для этого обе части второго уравнения, умноженные на число |
a32 |
, вычтем из соответствующих частей |
||||||||||
′ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
третьего уравнения. В результате придем к системе вида |
|
|
|
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
x + a |
x + a |
|
x |
= b ; |
(19.1) |
|
|||||
|
11 |
1 |
12 |
2 |
13 |
3 |
1 |
|
|
|
||
|
|
|
′ |
|
′ |
|
|
′ |
; |
(19.2) |
(19) |
|
|
|
a22 x2 + a23 x3 = b2 |
||||||||||
|
|
|
|
|
a′′ |
x |
= b′′. |
|
(19.3) |
|
||
|
|
|
|
|
33 |
|
3 |
3 |
|
|
|
|
Если a33′′ = 0 и b3′′ ≠ 0 , то система (19) несовместна, следовательно, равносильная ей система (2) тоже несовместна. Если a33′′ = 0 и b3′′ = 0 , то уравнение (19.3) можно отбросить и мы окажемся в ситуации, аналогичной (16).
Пусть a33′′ ≠ 0 . Тогда из уравнения (19.3) найдем x3 = x3o . Подставим в уравнение (19.2) вместо x3 число x3o и найдем из полученного уравнения x2 = x2o . Подставим в уравнения (19.1) вместо x2 и x3 соответственно x2o и x3o и из полученного уравнения найдем x1 = x1o . Таким образом, в этом случае система (19) и, следовательно, система (2) имеет единственное решение (x1o , x2o , x3o) , т.е. является определенной:
M ={(x1o , x2o , x3o)}.
Изложенный выше метод Гаусса применим к произвольной системе m линейных уравнений с n неизвестными, т.е. к любой системе вида (1).
Задача 1.2. Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти ее решение с помощью формул Крамера; б) записать систему в матричной форме и решить ее матричным способом; в) решить систему методом Гаусса.
7x1 + 4x2 − x3 =13 ;3x1 + 2x2 +3x3 = 3 ;2x1 −3x2 + x3 = −10 .
Решение.
а) Найдем решение системы с помощью формул Крамера
x1 = ∆∆1 ; x2 = ∆∆2 ; x3 = ∆∆3 ,
где ∆ − определитель системы уравнений; ∆1 , ∆2 , ∆3 − вспомогательные определители системы уравнений. Вычислим ∆ , ∆1 , ∆2 , ∆3 , используя схему (6):
∆ = |
|
7 |
4 |
−1 |
|
= 7 2 1+ 4 3 2 +3 (−3) (−1) − |
|
|
|||||
|
3 |
2 |
3 |
|
||
|
|
2 |
−3 |
1 |
|
|
–(−1) 2 2 −4 3 1−3 (−3) 7 =14 + 24 +9 + 4 −12 + 63 =102 ;
∆=102 ≠ 0 система уравнений совместна.
∆1 = |
|
13 |
4 |
−1 |
|
=13 2 1+ 4 3 (−10) +3 (−3) (−1) − |
|
|
|||||
|
3 |
2 |
3 |
|
||
|
|
−10 |
−3 |
1 |
|
|
−(−1) 2 (−10) −4 3 1−3 (−3) 13 = 26 −120 +9 − 20 −12 + 117 = 0 ,
∆2 = |
|
7 |
13 |
|
−1 |
|
= 7 3 1+13 3 2 +3 (−10) (−1) − |
||
|
|
||||||||
|
3 |
3 |
3 |
|
|||||
|
|
|
|
2 |
−10 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
−(−1) 3 2 −13 3 1−3 (−10) 7 = 21+78 +30 +6 −39 + 210 = 306 , |
∆3 = |
|
7 |
4 |
13 |
|
= 7 2 (−10) + 4 3 2 +3 (−3) 13 − |
|||
|
|
||||||||
|
3 |
2 |
3 |
|
|||||
|
|
2 |
|
−3 |
−10 |
|
|
|
|
|
|
|
|
|
|
|
−13 2 2 −4 3 (−10) −3 (−3) 7 = −140 + 24 −117 −52 +120 + 63 = −102 , |
|||||||||
∆ =102 , ∆1 = 0 , ∆2 = 306 , ∆3 = −102 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
= ∆1 |
= |
|
0 |
= 0 , |
x |
= ∆2 = |
|
306 |
= 3 , |
x |
= ∆3 |
= −102 = −1; |
|||
102 |
102 |
|||||||||||||||
1 |
∆ |
|
|
2 |
∆ |
|
|
|
3 |
∆ |
102 |
|||||
|
|
|
|
|
|
x1 = 0 , x2 = 3 , x3 = −1 . |
|
|
||||||||
б) Запишем систему в матричной форме и решим ее матричным способом. Матрица системы имеет вид |
||||||||||||||||
|
|
|
|
|
|
|
7 |
4 |
−1 |
|
|
|
||||
|
|
|
|
|
|
|
|
3 |
2 |
3 |
|
|
|
|
||
|
|
|
|
|
|
Α = |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
−3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим матрицы-столбцы неизвестных и свободных членов системы:
|
x1 |
|
|
|
|
13 |
|
|
X = |
x |
|
; |
Β = |
|
3 |
. |
|
|
|
2 |
|
|
|
|
|
|
|
x |
|
|
|
|
−10 |
|
|
|
|
3 |
|
|
|
|
|
|
Тогда матричная форма системы имеет вид
ΑX = B .
Найдем матрицу-столбец неизвестных по формуле
X=Α−1B .
Для этого найдем обратную матрицу Α−1 по формуле
|
|
Α11 |
Α21 |
Α31 |
|
|||
Α−1 = |
1 |
Α |
Α |
|
Α |
|
. |
|
|
|
22 |
32 |
|||||
|
|
12 |
|
|
|
|||
|
∆ |
Α |
Α |
23 |
Α |
33 |
|
|
|
|
|
13 |
|
|
|
||
Вычислим алгебраические дополнения элементов матрицы А:
Α = (−1)1+1 |
|
2 3 |
= 2 1−3 (−3) =11 , |
|||||||||||||||
11 |
|
|
−3 |
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
Α = (−1)1+2 |
|
|
|
3 3 |
|
= −(3 1−3 2)= 3 , |
||||||||||||
|
|
|
||||||||||||||||
12 |
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1+3 |
|
|
|
|
|
3 |
2 |
|
= 3 (−3) −2 2 = −13 ; |
|||||||||
|
|
|
|
|
||||||||||||||
Α = (−1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
13 |
|
|
|
|
|
|
2 |
−3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
4 −1 |
|
= −(4 1−(−1) (−3))= −1, |
|||||||||||
Α21 = (−1)2+1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
−3 |
1 |
|
|
|
||||||
Α22 = (−1)2+2 |
|
|
|
|
7 −1 |
|
= 7 1−(−1) 2 = 9 , |
|||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
||
Α23 = (−1)2+3 |
|
|
7 4 |
|
|
= −(7 (−3) − 4 2)= 29 ; |
||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
−3 |
|
|
|
|||||
|
|
|
4 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Α31 |
= (−1)3+1 |
|
= 4 3 −(−1) 2 =14 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Α32 |
= (−1)3+2 |
|
|
7 −1 |
|
= −(7 |
3 −(−1) 3)= −24 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Α33 |
= (−1)3+3 |
|
|
7 4 |
|
= 7 2 −4 3 = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
11 |
|
−1 |
14 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Α |
−1 |
= |
|
|
|
|
|
|
|
|
−24 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
9 |
|
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
102 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−13 |
29 |
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
11 |
|
−1 |
|
|
14 |
|
13 |
|
|
|
1 |
11 13 +(−1) 3 +14 (−10) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X=Α |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
|
|
|
|
3 |
|
9 |
|
|
−24 |
|
3 |
|
= |
|
|
|
|
3 13 +9 3 +(−24) |
(−10) |
|
= |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
102 |
|
|
|
102 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
2 |
|
|
|
|
|
|
−13 13 + 29 3 + 2 |
(−10) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−13 |
|
|
|
|
−10 |
|
|
|
|
|
|
|
||||||||||
|
|
1 |
143 −3 −140 |
|
|
|
1 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
39 + |
27 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
= |
|
|
|
240 |
= |
|
|
|
|
306 |
|
= |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
102 |
|
102 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
−169 |
+87 −20 |
|
|
|
|
−102 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
|
3 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
−1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
т.е. x1 = 0 , x2 = 3 , x3 = −1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
в) Решим систему методом Гаусса. Исключим неизвестное х1 |
из второго и третьего уравнений системы. Для этого обе |
|||||||||||||||||||||||||||||||||||||||||||||
части первого уравнения, умноженные на число 3, вычтем из соответствующих частей второго уравнения, умноженных на число 7; затем обе части первого уравнения, умноженные на число 2, вычтем из соответствующих частей третьего уравнения, умноженных на число 7. В результате получаем систему вида
7x + 4x − x =13 ; |
||
|
1 |
2 3 |
|
2x2 + 24x3 = −18 ; |
|
|
−29x +9x = −96 . |
|
|
2 |
3 |
Разделим обе части второго уравнения полученной системы на общий множитель 2:
7x + 4x − x =13 ; |
||
|
1 |
2 3 |
|
x2 +12x3 = −9 ; |
|
|
−29x +9x = −96 . |
|
|
2 |
3 |
Исключим неизвестное х2 из третьего уравнения системы. Для этого к обеим частям третьего уравнения прибавим соответствующие части второго уравнения, умноженные на число 29:
7x1 + 4x2 − x3 =13;
2+12x3 = −9 ;
357x = −357 .
3x
Из последнего уравнения системы находим x3 = −1 . Подставляя во второе уравнение вместо x3 число −1 , получаем x2 −12 = −9 , откуда x2 = 3 . Подставляя в первое уравнение вместо x2 и x3 числа 3 и −1 , получаем 7x1 +12 +1 =13 , откуда x1 = 0 . Итак, x1 = 0 , x2 = 3 , x3 = −1 .
Задача 1.2 решена.
1.3. ОДНОРОДНАЯ СИСТЕМА ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧЕТЫРЬМЯ НЕИЗВЕСТНЫМИ
Рассмотрим однородную систему трех линейных уравнений с четырьмя неизвестными.
a x + a x + a x + a x = 0 ; |
|
||||||||
|
11 |
1 |
12 |
2 |
13 |
3 |
14 |
4 |
|
a21x1 + a22 x2 + a23 x3 + a24 x4 = 0 ; |
(20) |
||||||||
a x + a x |
+ a x |
+ a x = 0 . |
|
||||||
|
31 |
1 |
32 |
2 |
33 |
3 |
34 |
4 |
|
Система (20) совместна, ибо имеет нулевое решение х1 = 0, х2 = 0, |
х3 = 0, |
х4 = 0 . |
|
|
|
|
|||
Как уже отмечалось выше, систему (20) можно решить методом Гаусса. При этом в процессе решения число уравнений системы (20) может лишь уменьшаться (за счет отбрасывания уравнений, у которых коэффициенты при всех неизвестных и свободный член равны нулю, если такие уравнения появляются в ходе преобразований системы уравнений). Следовательно, система (20) в конечном итоге приводится к трапецеидальному виду а, значит, является неопределенной.
Нулевое решение системы (20) называется также тривиальным решением. Если хотя бы одна из компонент решения ξ1 , ξ2 , ξ3 , ξ4 системы (20) отлична от нуля, то такое решение называется нетривиальным.
Задача 1.3. Найти множество решений однородной системы трех линейных уравнений с четырьмя неизвестными. Выписать три конкретные нетривиальные решения и проверить одно из них.
3x1 −5x2 + 2x3 +5x4 = 0 ;7x1 −4x2 + x3 +3x4 = 0 ;5x1 +7x2 −4x3 −9x4 = 0 .
Решение. Применим метод Гаусса. Исключим из второго и третьего уравнений системы неизвестное x1 . Для этого из
обеих частей второго уравнения, умноженных на число 3, вычтем соответствующие части первого уравнения, умноженные на число 7; затем из обеих частей третьего уравнения, умноженных на число 3, вычтем соответствующие части первого уравнения, умноженные на число 5. В результате приходим к системе вида
3x −5x + 2x +5x = 0 ; |
||||
|
1 |
2 |
3 |
4 |
|
23x2 −11x3 −26x4 = 0 ; |
|||
|
46x |
−22x |
−52x = 0 . |
|
|
2 |
3 |
|
4 |
В полученной системе уравнений исключаем из третьего уравнения неизвестное x2 . Для этого из обеих частей третьего уравнения вычтем соответствующие части второго уравнения, умноженные на число 2:
3x −5x + 2x +5x = 0 ; |
||||
|
1 |
2 |
3 |
4 |
|
23x2 −11x3 −26x4 = 0 ; |
|||
|
|
|
0 x3 +0 x4 = 0 . |
|
|
|
|
||
Последнее уравнение этой системы можно отбросить:
3x −5x + 2x +5x = 0 ; |
||||
|
1 |
2 |
3 |
4 |
|
23x2 −11x3 −26x4 = 0. |
|||
|
|
Пусть x3 = γ , |
x4 = µ (γ,µ R) . Подставляя во второе уравнение системы вместо x3 и x4 соответственно γ и µ, получа- |
||||||||||||||||||||||||||||||||||||||||
ем |
23x |
−11γ −26µ = 0 , откуда x |
2 |
= |
|
11 |
γ + |
26 |
|
µ. Подставляя в первое уравнение системы вместо x |
, x |
, x соответственно |
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
23 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
11 |
γ + |
26 |
µ , |
γ , µ получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
23 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
− |
55 |
γ − |
130 |
µ+ 2γ +5µ = 0 , |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
23 |
|
|
23 |
|
|
|
|
|
|
|
|
|
||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
3 |
γ + |
5 |
µ . |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
23 |
|
23 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Итак, |
x |
= |
3 |
|
γ + |
5 |
µ , x = |
11 |
γ+ |
|
26 |
µ, |
x = γ , x |
4 |
= µ , где γ , µ − произвольные действительные числа (параметры). Следо- |
||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
23 |
23 |
2 |
23 |
|
23 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
вательно, исходная система имеет бесконечное множество решений вида |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
11 |
|
|
|
26 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M = |
|
|
γ + |
|
|
µ |
, |
|
|
|
γ + |
|
|
µ, γ , µ | |
γ,µ R . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
23 |
23 |
23 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Запишем три конкретные нетривиальные решения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
• |
положим γ = 23, µ= 0, тогда x1 = 3, x2 = 11, x3 = 23, x4 = 0; |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
• |
положим γ = 0, µ= 23, тогда x1 = 5, x2 = 26, x3 = 0, x4 = 23; |
|
|
|
|
||||||||||||||||||||||||||||||||||||

• положим γ = 1, µ= 1, тогда x1 = 238 , x2 = 3723 , x3 = 1, x4 = 1.
Проверим первое решение x1 = 3, x2 = 11, x3 = 23, x4 = 0, для чего подставим его в уравнения исходной системы:
3 3 −5 11+ 2 23 +5 0 = 9 −55 + 46 = 0 , 0 = 0; 7 3 −4 11+ 23 +3 0 = 21− 44 + 23 = 0, 0 = 0; 5 3 +7 11−4 23 −9 0 =15 + 77 −92 = 0, 0 = 0.
Задача 1.3 решена.
1.4. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Рассмотрим квадратную матрицу порядка 3
|
a11 |
a12 |
a13 |
|
Α = |
a |
a |
a |
. |
|
21 |
22 |
23 |
|
|
a |
a |
a |
|
|
31 |
32 |
33 |
|
Число λ называется собственным значением матрицы А, если существует ненулевая матрица-столбец
x1 X = x2 ,x3
такая что
ΑX=λX , |
(21) |
при этом, матрица-столбец Х называется собственным вектором матрицы А, отвечающим собственному значению λ . Проведя умножение в обеих частях (21) и приравнивая соответствующие элементы полученных матриц-столбцов, приходим к скалярной записи соотношения (21):
a11x1 + a12 x2 + a13 x3a21x1 + a22 x2 + a23 x3a31x1 + a32 x2 + a33 x3
или
=λx1 ;
=λx2 ;
=λx3.
(a11 −λ)x1 + a12 x2 + a13 x3 = 0 ; |
|
||||||
a21x1 +(a22 −λ)x2 + a23 x3 = 0 ; |
(22) |
||||||
a x |
+ a x |
+(a |
−λ)x = 0. |
|
|||
|
31 |
1 |
32 |
2 |
33 |
3 |
|
Таким образом, число λ является собственным значением матрицы А тогда и только тогда, когда система уравнений (22) с таким λ имеет хотя бы одно ненулевое решение. При этом каждое такое ненулевое решение X1,3 = (x1 , x2 , x3 ), если его протранспонировать, т.е. матрица-столбец
|
|
x1 |
|
|
X=XT |
= |
x |
2 |
|
1,3 |
|
|
|
|
|
|
x |
|
|
|
|
|
3 |
|
является собственным вектором матрицы А, отвечающим данному собственному значению λ .
В матричной форме система (22) имеет вид |
|
(Α−λΕ)X=0 , |
(23) |
где Е – единичная матрица порядка 3.
Система (22) – это система трех линейных уравнений с тремя неизвестными.
Если определитель ∆ = det (Α−λΕ) системы (22) отличен от нуля, то она, согласно правилу Крамера, имеет единственное решение x1 = 0, x2 = 0, x3 = 0. Следовательно, система (22) имеет ненулевые решения в том и только том случае, когда
det (Α −λΕ)= 0 . |
(24) |
Итак, собственными значениями матрицы А являются корни уравнения (24).
Уравнение (24) называется характеристическим уравнением матрицы А, его левая часть, т.е. det (Α−λΕ) – характе-
ристическим многочленом матрицы А; решения уравнения (24) – характеристическими числами матрицы А.
Заметим, что

|
a11 −λ |
a12 |
|
a13 |
|
|
|||
Α−λΕ = |
|
a |
a |
−λ |
|
a |
23 |
. |
(25) |
|
|
21 |
22 |
|
|
|
|
|
|
|
|
a |
a |
|
a |
|
−λ |
|
|
|
|
31 |
32 |
33 |
|
|
|
||
Матрица (25) называется характеристической матрицей матрицы А. Учитывая (25), характеристическое уравнение (24) можно записать в виде
a11 −λ |
a12 |
a13 |
|
|
|
|
|
||||
a21 |
a22 −λ |
a23 |
|
= 0 . |
(26) |
a31 |
a32 |
a33 −λ |
|
|
|
Из вышесказанного следует, что если ставится задача о нахождении собственных значений и собственных векторов матрицы А, то нужно:
1)записать характеристическое уравнение (26) и найти его корни (тем самым будут найдены собственные значения матрицы А);
2)для каждого собственного значения λ записать систему линейных однородных уравнений (22) и найти ее ненулевые
решения а затем протранспонировать найденные ненулевые решения (тем самым будут найдены собственные векторы матрицы А, отвечающие данному собственному значению λ ).
Все вышесказанное в этом пункте о собственных значениях и собственных векторах квадратной матрицы порядка 3 естественным образом переносится на случай квадратной матрицы произвольного порядка n.
Задача 1.4. Определить собственные значения и собственные векторы матрицы третьего порядка.
4 |
1 |
−2 |
|
|
|
1 |
4 |
2 |
|
Α = |
. |
|||
|
−2 |
2 |
1 |
|
|
|
|||
Решение. Запишем характеристическое уравнение матрицы А:
|
|
|
|
|
|
4 −λ |
1 |
−2 |
|
= 0 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
4 −λ |
2 |
|
|
|
|
|
|
|
|
−2 |
2 |
1−λ |
|
|
Раскроем левую часть уравнения |
|
|
|
|
||||||
|
4 −λ |
1 |
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
4 −λ |
2 |
|
= (4 −λ)(4 −λ)(1−λ) +1 2 (−2) + |
|
|
|
||
|
−2 |
2 |
1−λ |
|
|
|
|
|
|
|
+1 2 (−2) −(−2) (4 −λ) (−2) −1 1 (1−λ) − 2 2 (4 −λ) =
=(16 −8λ +λ2 )(1−λ) − 4 − 4 −16 + 4λ −1+λ −16 + 4λ =
=16 −8λ +λ2 −16λ +8λ2 −λ3 +9λ − 41 = −λ3 +9λ2 −15λ − 25 .
Характеристическое уравнение принимает вид
−λ3 +9λ2 −15λ − 25 = 0 ,
или
λ3 −9λ2 +15λ + 25 = 0 .
Найдем методом подбора целый корень данного уравнения, исходя из того, что целые корни уравнения, если они есть, находятся среди делителей свободного члена. Делители свободного члена: ±1 , ±5 , ± 25 . Подставляя поочередно эти делители
в уравнение, приходим к выводу, что λ1 = −1 − корень данного уравнения. Следовательно, левая часть уравнения делится нацело на двучлен λ −λ1 = λ +1 :
_ λ3 −9λ2 +15λ + 25 λ +1
λ3 + λ2 λ2 −10λ + 25
_ −10λ2 +15λ + 25
−10λ2 −10λ _ 25λ + 25
25λ + 25
0
Тогда уравнение принимает вид
(λ +1 )( λ2 −10λ + 25) = 0 . |
|
|
|
|
Приравниваем второй множитель в левой части уравнения нулю: λ2 −10λ + 25 = 0 или |
(λ −5 )2 = 0 , т.е. |
λ2 = 5 . Итак, мат- |
||
рица А имеет два собственных значения λ1 = −1, λ2 = 5 . |
|
|
|
|
Запишем систему уравнений (22): |
|
|
|
|
(4 −λ)x1 + x2 −2x3 = 0 ; |
|
|||
|
x1 +(4 −λ)x2 + 2x3 = 0 ; |
(27) |
||
−2x |
+ 2x |
+(1−λ)x = 0. |
|
|
|
1 |
2 |
3 |
|
Найдем собственные векторы матрицы А, отвечающие собственному значению λ1 = −1. Для этого запишем систему (27) при
λ = λ1 :
5x1 + x2 −2x3 = 0 ; |
|
|||
x1 +5x2 + 2x3 = 0 ; |
(28) |
|||
−2x |
+ 2x |
+ 2x = |
0. |
|
|
1 |
2 |
3 |
|
Найдем ненулевые решения системы (28):
|
5x1 + x2 −2x3 = 0 ; |
|
x1 − x2 − x3 = 0 ; |
|
|
|
||||||
|
x1 +5x2 + 2x3 = 0 ; |
x1 +5x2 + 2x3 = 0 ; |
|
|
|
|||||||
|
−2x1 + 2x2 + 2x3 = 0; |
|
5x1 + x2 −2x3 = 0; |
|
|
|
||||||
|
|
|
|
|
|
|
x |
= |
γ |
; |
|
|
|
|
|
|
|
|
|
|
|
||||
x1 |
− x2 |
− x3 = 0 ; |
|
|
|
|
1 |
2 |
|
|
|
|
x1 − x2 − x3 = 0 ; |
|
|
|
γ |
|
|||||||
|
6x2 +3x3 = 0 ; |
|
|
|
|
|
|
|||||
|
|
2x |
+ x = 0 ; |
|
x2 |
= − |
|
|
; |
|||
2 |
||||||||||||
|
6x |
+3x = 0; |
|
2 |
3 |
|
|
= γ |
, γ R . |
|||
|
2 |
3 |
|
|
|
|
x |
|||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, множество ненулевых решений системы (28) имеет вид
M |
|
= |
γ |
, − |
γ |
, γ |
|
| |
γ R , γ ≠ 0 . |
|
|
2 |
|
||||||
|
1 |
2 |
|
|
|
|
|||
Следовательно, множество собственных векторов матрицы А, отвечающих собственному значениюλ1 = −1, имеет вид
|
|
γ |
|
γ |
|
T |
|
|
S1 |
|
|
|
| γR , γ ≠ 0 |
|
|||
= |
|
, − |
|
, γ |
|
. |
||
2 |
2 |
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Найдем собственные векторы матрицы А, отвечающие собственному значению λ2 = 5 . Для этого запишем систему (27) при
λ = λ2 :
|
|
|
|
|
|
|
−x + x −2x = 0 ; |
|
||||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
x1 |
− x2 + 2x3 = 0 ; |
(29) |
|||
|
|
|
|
|
|
|
−2x |
+ 2x |
−4x = |
0. |
||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
Найдем ненулевые решения системы (29): |
|
|
|
|
|
|
|
|
|
|
||
−x + x −2x = 0 ; |
|
|
x |
|
= β− |
2γ ; |
|
|
||||
|
1 |
2 |
3 |
|
x1 − x2 + 2x3 |
1 |
|
|
|
|
|
|
x1 |
− x2 + 2x3 = 0 ; |
|
= 0 x2 = β, β R ; |
|
|
|||||||
−2x |
+ 2x |
−4x = |
0; |
|
x |
|
= γ , γ R. |
|
|
|||
|
1 |
2 |
3 |
|
|
3 |
|
|
|
|
|
|
Таким образом, множество ненулевых решений системы (29) имеет вид
M2 ={(β−2γ , β, γ) | β, γ R ; β2 + γ2 ≠ 0}.
Следовательно, множество собственных векторов матрицы А, отвечающих собственному значению λ2 = 5 , имеет вид
S2 ={(β−2γ , β, γ)T | β, γ R ; β2 + γ2 ≠ 0}
(заметим, что условие β2 + γ2 ≠ 0 означает, что β и γ не обращаются одновременно в нуль).
Задача 1.4 решена.
Контрольная работа 2
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
2.1. ПРЯМАЯ НА ПЛОСКОСТИ
Понятия точки, прямой и плоскости относятся к неопределяемым (первичным) понятиям математики.
Рассмотрим прямую d на плоскости (рис. 1) и введем на этой плоскости декартову прямоугольную систему координат (ДПСК) (Декарт Р. (1596 − 1650) − французский философ, математик, физик, физиолог):
Рис. 1
Пусть ϕ − угол наклона прямой d к положительному направлению оси Οx .
Угловой коэффициент прямой d :: = тангенс угла наклона прямой d к положительному направлению оси Οx :
k = tg ϕ .
Пусть b − величина отрезка, отсекаемого прямой d на оси Οy . Выведем уравнение прямой d, учитывая, что она имеет угловой коэффициент k и отсекает на оси Οy отрезок величиной b . Пусть M (x, y) − переменная точка с текущими коор-
динатами x, y . Тогда, как видно из прямоугольного треугольника BCM , |
|
||||||
M d |
|
y −b |
= tg ϕ, |
|
|||
|
|
|
|
||||
т.е. |
|
x |
|
|
|||
|
y −b |
|
|
|
|||
M d |
|
= k |
|
||||
|
x |
|
|||||
или |
|
|
|
||||
|
|
|
|
y = kx +b . |
(30) |
||
|
|
|
|
|
|
||
Таким образом, уравнение прямой, имеющей угловой коэффициент k |
и отсекающей на оси ординат отрезок величиной b , за- |
||||||
писывается в виде (30). |
|
|
|
|
|
|
|
Уравнение вида (30) называется уравнением прямой с угловым коэффициентом. |
|
||||||||
Возьмем точку M0 (x0 , y0 ), |
принадлежащую прямой d. Выведем уравнение прямой d, учитывая что она проходит через |
||||||||
точку M0 (x0 , y0 ) и имеет угловой коэффициент k . Из прямоугольного треугольника M0 AM видно, что |
|
||||||||
|
|
|
M d |
MA = tg ϕ . |
|
|
|||
|
|
|
|
|
|
M0 A |
|
|
|
Но MA = y − y0 , M0 A = x − x0 , |
tg ϕ = k . Следовательно, |
|
|
|
|
||||
|
|
|
M d y − y0 = k |
|
|
||||
|
|
|
|
|
|
|
x − x |
|
|
или |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
y − y0 = k (x − x0 ) . |
|
|
|
|
|
|
|
|
|
|
(31) |
|
Таким образом, уравнение прямой, проходящей через данную точку M0 (x0 , y0 ) |
и имеющей заданный угловой коэффициент |
||||||||
k , записывается в виде (31). |
|
|
|
|
|
|
|
|
|
Заметим, что уравнение (31) можно записать в виде (30) ( b = y0 −kx0 ). |
|
|
|||||||
Уравнение (31) выведено в предположении, что ϕ ≠ 0 , ϕ ≠ |
π . Если ϕ = 0 , т.е. прямая d параллельна оси Οx , то уравне- |
||||||||
|
|
|
|
|
|
|
2 |
|
|
ние прямой d имеет вид y = y |
0 |
(при условии, что M |
0 |
d ). Если ϕ = π , т.е. прямая d перпендикулярна к оси Οx |
(в этом |
||||
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
случае угловой коэффициент прямой d не существует, так как |
tg ϕ при ϕ = π |
не определен), то уравнение прямой d имеет |
|||||||
|
|
|
|
|
|
|
2 |
|
|
вид x = x0 (в этом случае говорят, что угловой коэффициент прямой d равен бесконечности). Рассмотрим на плоскости, снабженной ДПСК, прямую d (рис. 2).
РИС. 2
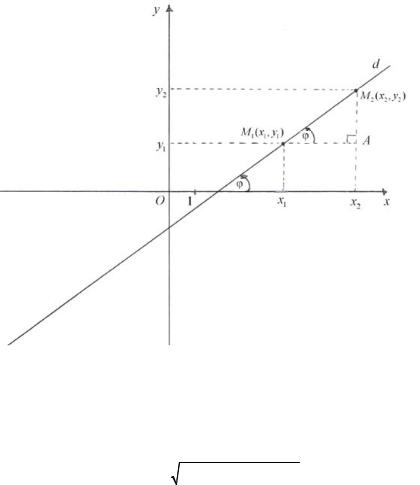
Рассмотрим две точки M1 (x1, y1 ), M2 (x2 , y2 ), принадлежащие прямой d. Из прямоугольного треугольника M1 AM2 видно в силу теоремы Пифагора (Пифагор (ок. 580 − 500 до н.э.) − древнегреческий математик, философ), что расстояние между точками M1 (x1, y1 ) и M2 (x2 , y2 ), т.е. длина отрезка M1M2 , определяется формулой
|
M |
M |
2 |
|
= |
(x − x )2 |
+(y |
2 |
− y )2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
2 |
1 |
|
1 |
|
|
|
|
||
Из ∆ M1AM2 также видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = tg ϕ = |
y2 − y1 |
. |
(32) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x |
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
