Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тамбовский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

k_Fomin

.pdf

Скачиваний:

Добавлен:

20.03.2016

Размер:

1.26 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

где a0 , a1, ..., an−1, an − некоторые числа, называемые коэффициентами многочлена, при этом a0 ≠ 0 .

Часть слагаемых в выражении для многочлена может отсутствовать. Это означает, что коэффициенты при соответствующих степенях многочлена равны нулю. Например, выражение 5x3 −2x +11 = 0 является многочленом 3-й степени

( a0 = 5; a1 = 0; a2 = −2; a3 =11 ).

Заметим, что

Действительно,

lim P (x) = lim a		xn + a xn−1 +... + a						x + a			=
x→∞ n	x→∞ 0		1			n−1			n
	= lim xn	a	+	a1	+... +	an−1	+	an		= (∞ a ) =

		0		x		xn−1					0
	x→∞							xn

В силу (69) отношение

	∞ , если a0	> 0;
lim Pn (x) =		< 0.
x→∞	−∞, если a0	< 0.

∞ ,	a0 > 0;
	a0 < 0.
−∞,	a0 < 0.

Pn (x)

Qm (x)

(69)

(70)

двух многочленов Pn (x) и Qm (x) представляет собой при x → ∞ неопределенность типа ∞∞ (так говорят по той причине,

что предел такого отношения может оказаться равным конечному ненулевому числу, нулю или бесконечности, в зависимости от соотношения по величине между n и m ).

Для раскрытия такой неопределенности надо числитель и знаменатель дроби (70) разделить на xl , где l = max{n, m}, а

затем применить основную теорему о пределах.

Если вычисляется предел отношения (70) при x → x0 и это отношение представляет собой при x → x0 неопределен-

ность типа 00 , то для раскрытия такой неопределенности числитель и знаменатель дроби (70) делят на двучлен x − x0 (такое

деление корректно, ибо x → x0 , но x ≠ x0 , следовательно, x − x0 ≠ 0 ; кроме того, такое деление осуществляется нацело, ибо если x0 − корень многочлена, то данный многочлен делится нацело на x − x0 ; такое деление можно провести по правилу

уголка или по схеме Горнера (Горнер В.Д. (1786 − 1837) − английский математик)). При вычислении некоторых пределов используется первый замечательный предел

lim	sin x	=1	(71)
	x
x→0

и второй замечательный предел

В силу (71)

Если в (72) произвести замену α = 1x

		1	x
lim 1	+			= e .	(72)
		x
x→∞

lim tg x =1.

x→0 x

( α → 0 при x → ∞ ), то второй замечательный предел можно записать в виде

		1
	lim (1+α)		α	= e .
	α→0
Функция y = f (x)	называется непрерывной в точке x0	D( y) , если существует lim f (x) = f (x0 ) .
				x→x0
Функция y = f (x)	называется непрерывной на множестве D D( y) , если она непрерывна в каждой точке этого мно-

жества.

Справедлива основная теорема о непрерывных функциях.

Теорема. Пусть функции u = u(x) , v = v(x) непрерывны на множестве D D( y) . Тогда сумма, разность, произведение и частное этих функций тоже непрерывны на множестве D (в случае частного предполагается, что v(x) ≠ 0 для

x D ).

Основные элементарные функции (см. прил. 1) непрерывны на своей области определения.

Элементарная функция :: = функция, полученная с помощью конечного числа арифметических действий над основны-

ми элементарными функциями и конечного числа операций взятия функции от функции. Например, функция

y = 5sin3 x +ln2 x x3 +1

является элементарной.

Каждая элементарная функция непрерывна на своей области определения.

Из определения непрерывности функции в точке следует, что при вычислении предела при x → x0 непрерывной в точке x0 функции f (x) , достаточно в выражение для f (x) подставить вместо x значение x0 .

Например,

lim(2x2 − x +5) = 2 32 −3 +5 = 20 .

x→3

Задача 3.2. Вычислить пределы функций, не пользуясь правилом Лопиталя:

а)

lim

9x5

−4x3 + 2

;

б)

lim

3x2 −10x +8

;

2x2 −

3x −

x→∞ 3x4 −2x +3

x→2

в)

lim

1−cos5x

;

г)

lim

3x −1 2x−4

x tg 2x

3x +

x→0

x→∞

Решение.

9x5 −4x3 + 2

∞

9 −

а)

A = lim

= lim

= ∞ ,

3x4 −2x +3

x→∞

∞

x→∞

−

A = ∞ ;

б)

A = lim

3x2 −10x +8

3x −4

0, 4 ;

= lim

2x2 −3x −2

x→2

−

3x2 −10x +8

x −2

−

2x2 −3x −2

x −2

3x2 −6x

3x −4

2x2 −4x

2x +1

−−4x +8

−x −2

−4x +8

x −2

A = 0, 4 ;

в)

A = lim

1−cos5x

x tg 2x

x→0

(1−cos 2α = 2sin2 α ;

1−cos5x = 2sin

)

5x 2

sin

25x2

sin

2sin2

= lim

lim

x tg 2x

tg 2x

x→0

tg 2x

4 x

→0

= 6

= 6, 25 ;

A = 6, 25 ;

г)

A = lim

3x −1 2x−4

∞

= (1

) =

3x + 2

x→∞

(

3x −1

(3x + 2) −2 −1

=1+

−3

)

3x +

3x + 2

−3

2x−4

−3

3x+2

−3

(2x−4)

−3

3x+2

= lim

+ 2

x→∞

3x + 2

−3(2x−4)

−3

3x+2 3x+2

= lim

−3

3x +

x→∞

3x+

lim

−3(2x−4)

−3

2 x→∞

3x+2

−3

= e

−2

lim

3x +

x→∞

A = e−2 .

Задача 3.2 решена.

3.3. ТОЧКИ РАЗРЫВА ФУНКЦИИ, ИХ КЛАССИФИКАЦИЯ

3.3.1. ОДНОСТОРОННИЕ ПРЕДЕЛЫ ФУНКЦИИ В ТОЧКЕ

Правосторонний предел			f (x0 +0) функции	f (x) в точке x0		:: = предел функции f (x) в точке x0 , вычисленный при
условии, что x стремится к x0			справа, т.е. x стремится к x0 , оставаясь больше x0 :
				f (x0 +0) =	lim	f (x)
				x→x0 +0
(запись x → x0 +0 означает, что x стремится к x0 справа).
Левосторонний предел		f (x0 −0) функции f (x) в точке x0			:: = предел функции f (x) в точке x0 , вычисленный при ус-
ловии, что x стремится к x0		слева, т.е. x стремится к x0 , оставаясь меньше x0 :
				f (x0 −0) =	lim	f (x)
				x→x0 −0
(запись x → x0 −0 означает, что x стремится к x0 слева).
Правосторонний и левосторонний пределы функции f (x)					в точке называются односторонними пределами этой функ-
ции в данной точке.
			3.3.2. ПРИЗНАК СУЩЕСТВОВАНИЯ ПРЕДЕЛА ФУНКЦИИ В ТОЧКЕ
			lim f (x) = A ( f (x0 +0) , f (x0 −0))
			x→x0
						f (x0 +0) = f (x0 −0) = A .		(73)
			3.3.3. ПРИЗНАК НЕПРЕРЫВНОСТИ ФУНКЦИИ В ТОЧКЕ
Пусть функция f (x)	непрерывна в точке x0 , т.е. lim f (x) = f (x0 ) . Тогда в силу (73) f (x) непрерывна в точке x0
				x→x0
				( f (x0 +0) , f (x0 −0)) f (x0 +0) = f (x0 −0) = f (x0 ) .				(74)
Предельная точка x0	множества D( y) , называется точкой разрыва функции f (x) , если в этой точке функция							f (x) не
является непрерывной.
Из (74) видно, что x0	является точкой разрыва функции в следующих случаях:
1) существуют конечные односторонние пределы f (x0 +0) ,						f (x0 −0) и	f (x0 +0) = f (x0 −0) , но x0 D( y) ;	в этом
случае x0 называется устранимой точкой разрыва функции f (x) ;
2) существуют конечные односторонние пределы f (x0 +0) ,						f (x0 −0) , но	f (x0 +0) ≠ f (x0 −0) ; в этом случае	x0 на-
зывается точкой разрыва первого рода функции				f (x) (или точкой конечного разрыва); разность f (x0 +0) − f (x0 −0) назы-
вается скачком функции f (x) в точке x0 ;
3) хотя бы один из односторонних пределов				f (x0 +0) , f (x0 −0) равен бесконечности (не важно какого знака); в этом

случае x0 называется точкой разрыва второго рода функции f (x) (или точкой бесконечного разрыва).

Задача 3.3. Исследовать функцию y = f (x) на непрерывность:

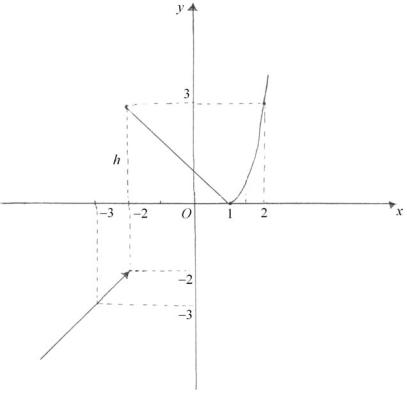
а) найти точки разрыва функции, если они существуют; б) найти односторонние пределы и скачок функции в точках разрыва; в) построить график функции.

		x,	x < −2;
			−2 ≤ x ≤1;
f (x) = −x +1,			−2 ≤ x ≤1;
	2	−1,	x >1.
x		−1,	x >1.

Решение.

а) Функция f (x) может иметь разрыв лишь в тех точках, при переходе через которые выражение для функции меняется, т.е. в точках x1 = −2 , x2 =1 . Проверим, будет ли x1 = −2 точкой разрыва:

	f (x1 +0) = f (−2 +0) =		lim	f (x) =			lim (−x +1) = 3 ;
			x→−2+0			x→−2+0
	f (x1	−0) = f (−2 −0) = lim f (x) =					lim x = −2 .
			x→−2−0				x→−2−0
Получили:	f (−2 +0) = 3 ; f (−2 −0) = −2 ,	но f (−2 +0) ≠ f (−2 −0) x1 = −2 − точка разрыва первого рода. Вычислим
скачок функции в точке x1 = −2 :
	h = f (−2 + 0) − f (−2 −0) = 3 −(−2) = 5 , h = 5 .
Исследуем точку x2 =1 :
	f (x	+0) = f (1+0) =	lim	f (x) =		lim (x2 −1) = 0 ;
	2		x→1+0			x→1+0
			x→1+0			x→1+0
	f (x2	−0) = f (1−0) =	lim	f (x) =		lim (−x +1) = 0 ;
			x→1−0			x→1−0
		f (x2 ) = f (1) = (−x +1)			x=1 = 0 .
		f (x2 ) = f (1) = (−x +1)			x=1 = 0 .
Получим:	f (1+0) = f (1−0) = f (1) функция f (x) непрерывна в точке x2 =1 .
б) f (−2 +0) = 3 ; f (−2 −0) = −2 ; h = 5 (см. а) ).
в) Построим график функции (рис. 41).

Рис. 41

Задача 3.3 решена.

3.4. ПРОИЗВОДНАЯ ФУНКЦИИ

Рассмотрим функцию y = f (x) , x D( y) . Пусть x0 − внутренняя точка множества D( y) , т.е. Oδ (x0 ) Oδ (x0 ) D( y) . Придадим x0 приращение ∆x , т.е. рассмотрим точку x0 +∆x (приращение ∆x должно быть достаточно малым, а именно, таким, чтобы x0 + ∆x D( y) ; приращение ∆x может быть как положительным, так и отрицательным). Тогда функ-

ция f (x) получит приращение ∆y = f (x0 + ∆x) − f (x0 ) .

Величина ∆y показывает насколько изменилась функция при переходе из точки x		в точку x + ∆x . Отношение	∆y −
	0	0	∆x
это средняя скорость изменения функции при изменении аргумента на участке [x0 , x0 +∆x]. А величина			∆x

lim	∆y		(75)
∆x→0	∆x
является мгновенной скоростью изменения функции f (x) в точке x0 . В различных прикладных задачах функция f (x)			опи-

сывает некий процесс, и важно знать скорость протекания этого процесса, т.е. необходимо работать с величинами вида (75). В связи с этим вводят следующее определение.

Производная функции f (x) в точке x0 :: = конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении приращения аргумента к нулю, если такой предел существует:

f ′(x0 ) = lim ∆y

∆x→0 ∆x

или, учитывая вид ∆y ,

		f ′(x0 ) = lim	f (x0 + ∆x) − f (x0 )	.
		f ′(x0 ) = lim		.
		∆x→0	∆x
Функция	f (x)	называется дифференцируемой в точке x0 , если она имеет в этой точке конечную производную.
Функция	f (x)	называется дифференцируемой на множестве D D( y) , если она дифференцируема в каждой точке

этого множества.

Пусть функция y = f (x) дифференцируема на множестве D D( y) . Тогда каждой точке x D можно поставить в соответствие производную f ′(x) функции f (x) во взятой точке x . Тем самым на множестве D задана функция y′ = f ′(x) ,

называемая производной функции f (x) .

Производную y′ = f ′(x) обозначают также символом dydx .

Операция нахождения производной f ′(x) функции f (x) называется дифференцированием.

При дифференцировании функции применяют основную теорему о производных.

Теорема. Пусть функции u = u(x) , v = v(x) дифференцируемы на множестве D D( y) . Тогда сумма, разность, произведение и частное этих функций тоже дифференцируемы на множестве D и справедливы формулы:

1)[u(x) +v(x)]′ = u′(x) + v′(x) ;

2)[u(x) −v(x)]′ = u′(x) −v′(x) ;

3)[u(x)v(x)]′ = u′(x)v(x) +u(x)v′(x) ;

	u(x)	′		′	′
4)			=	u (x)v(x) −u(x)v (x)

					[v(x)]2
	v(x)

(в случае частного предполагается, что v(x) ≠ 0 для x D ). Если f (x) ≡ C для x D( y) , то

5) (C )′ = 0 .

Из свойств 3), 5) следует, что

6) [Cu(x)]′ = Cu′(x) .

При нахождении производных функций используется также правило дифференцирования сложной функции, выраженное следующей теоремой.

Теорема. Пусть функция u = u(x) дифференцируема на множестве D D(u) , а функция y = y(u) дифференцируема на множестве u(D) . Тогда сложная функция y = y(u(x)) дифференцируема на множестве D и справедлива формула

y′x = yu′ u′x ,

(76)

т.е. производная сложной функции равна произведению производной этой функции по промежуточному аргументу u и производной промежуточного аргумента u по основному аргументу x .

Например, согласно правилу (76) производная функции y = sin3 x имеет вид

y′ = 3sin2 x (sin x)′ = 3sin2 x cos x

(данную функцию можно записать в виде y = u3 , u = sin x ).

Правило (76) распространяется на сложную

функцию, состоящую из более,

чем

двух, звеньев.

Например, если

y = y(w(u(x))) , то

′

(77)

yx = yw

wu ux .

Согласно правилу (77) производная функции y = ln cos3 x имеет вид

′

x (−sin x)

= cos3 x

3cos

(данную функцию можно представить в виде y = ln w , w = u3 , u = cos x ).

Укажем правило дифференцирования функции, заданной параметрически:

x = ϕ(t)

t T .

= ψ(t)

Пусть функции ϕ(t) и ψ(t) дифференцируемы

на

′

для

любого t T .

Пусть функция

множестве T и ϕ (t) ≠ 0

x = ϕ(t) имеет обратную функцию t = ϕ−1(x) . Тогда справедлива формула

′

y′

yx′

ψ (t)

yx′ =

или

ϕ′(t)

xt′

При дифференцировании функций используется таблица производных основных элементарных функций (см. прил. 3).

Задача 3.4. Найти производные первого порядка, используя правила вычисления производных:

а)

y = 5sin 2x −e4x ;

б) y = sin2 3x ;

1+sin 2x

в)

y =

;

г) {xy ==5sin3cos3tt;.

1−sin 2x

Решение.

а)

y′ = (5sin 2x −e4x )′ = 5 (sin 2x)′−(e4x )′ =

= 5cos 2x 2 −e4x 4 =10 cos 2x −4e4x ,

y′ =10 cos 2x − 4e4x ;

б)

y′ = (sin2 3x)′ = 2sin 3x cos 3x 3 = 3sin 6x

(использована формула тригонометрии 2sin αcos α = sin 2α ),

y′ = 3sin 6x ;

′

+sin 2x

в)

y′

(1−sin 2x)2

−sin 2x

cos 2x 2 (1−sin 2x) −(1+sin 2x) (−cos 2x) 2

(1−sin 2x)2

2cos 2x(1−sin 2x +1+sin 2x)

4cos 2x

(1−sin 2x)2

−sin 2x)2

′

4cos 2x

= (1−sin 2x)2

;

г) yx′

yt′

(3cos3 t)′

3 3cos2 t (−sin t)

ctg t ,

= −

x′

(5sin3 t)′

5 3sin2 t (cos t)

yx′

ctg t .

= −

Задача 3.4 решена.

3.5. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

Производная y

′

функции y = f (x) сама является функцией переменного x и, следовательно, может оказаться

f (x)

дифференцируемой по x . В связи с этим вводится следующее определение.

Производной второго

порядка или второй производной функции

f (x) называется производная от производной

′

этой функции:

f (x)

y′′(x) = [y′(x)]′

d 2 y

или

dx2

dx dx

Аналогично вводится понятие производной более высокого порядка:

n−1

y(n) (x) =

y(n−1)

(x) ′ или

n−1

dx dx

Задача 3.5. Для данной функции y = y(x)

и аргумента x0

вычислить y′′(x0 ) .

y = x2 cos x ;

π .

Решение.

y′ = (x2 )′cos x + x2 (cos x)′ = 2x cos x − x2 sin x ;

y′′ = (2x)′ cos x + 2x (cos x)′− (x2 )′ sin x − x2 (sin x)′ =

= 2 cos x − 2x sin x − 2x sin x − x2 cos x = (2 − x2 ) cos x − 4x sin x ;

y′′ = (2 − x2 ) cos x − 4x sin x ;

−

π2

−4

sin

= −2π,

y′′

= 2

cos

= −2π .

y′′

Задача 3.5 решена.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

I.Литература, рекомендуемая для изучения теоретической части курса

1.Ефимов, Н.В. Краткий курс аналитической геометрии : учебник. – 13-е изд., стереотип. / Н.В. Ефимов. – М. : Физ-

матлит, 2003. – 240 с.

2.Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры : учебник. – 9-е изд., перераб. / Д.В. Беклеми-

шев. – М. : Физматлит, 2001. – 376 с.

3.Бермант, А.Ф. Краткий курс математического анализа : учебник. – 10-е изд., стереотип. / А.Ф. Бермант, И.Г. Арама-

нович. – СПб. : Лань, 2003. – 736 с.

4.Пискунов, Н.С. Дифференциальное и интегральное исчисления : учеб. пособие для втузов. – В 2 т. / Н.С. Пискунов.

–М. : Интеграл-Пресс, 2004. – Т. 1. – 416 с.

5.Щипачев, В.С. Основы высшей математики. – 4-е изд., стереотип. / В.С. Щипачев. – М. : Высш. шк., 2001. – 479 с.

6.Демидович, Б.П. Краткий курс высшей математики : учеб. пособие для вузов / Б.П. Демидович, В.А. Кудрявцев. – М.

:Астрель, 2003. – 656 с.

7.Фихтенгольц, Г.М. Основы математического анализа. – В 2 т. 7-е изд. / Г.М. Фихтенгольц. – М. : Физматлит, 2002. –

Т. 1. – 416 с.

II.Литература, рекомендуемая для изучения

практической части курса

1.Зимина, О.В. Высшая математика. – 2-е изд., испр. / О.В. Зимина [и др.]. – М. : Физматлит, 2001. – 368 с. (Решебник).

2.Клетеник, Д.В. Сборник задач по аналитической геометрии. – 16-е изд., испр. / Д.В. Клетеник. – СПб. : Мифрил, 2001. – 208 с.

3.Цубербиллер, О.Н. Задачи и упражнения по аналитической геометрии. – 31-е изд., стереотип. / О.Н. Цубербиллер. –

СПб. : Лань, 2003. – 336 с.

4.Сборник задач по аналитической геометрии и линейной алгебре. – 2-е изд., перераб. / Л.А. Беклемишева [и др.]. –

М. : Физматлит, 2001. – 496 с.

5.Щипачев, В.С. Задачник по высшей математике : учеб. пособие для вузов. – 4-е изд., стереотип. / В.С. Щипачев. – М.

:Высш. шк., 2004. – 304 с.

6.Демидович, Б.П. Сборник задач и упражнений по математическому анализу : учеб. пособие для вузов / Б.П. Демидо-

вич. – М. : Астрель, 2004. – 558 с.

7.Сборник индивидуальных заданий по высшей математике. – В 3 ч. / А.П. Рябушко [и др.]. – Минск : Вышэйшая шко-

ла, 1990. – Ч. 1. – 270 с.

ПРИЛОЖЕНИЯ

Приложение 1

	ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
1.	Степенная функция:			y = xα , α R .
				y = xα , α R .
2.	Показательная функция:			y = ax , a R, a > 0, a ≠1.
				y = ax , a R, a > 0, a ≠1.
3.	Логарифмическая функция:					x ::= x = a y ).
	y = log	a	x,	a R, a > 0, a ≠1 ( y = log	a	x ::= x = a y ).
4.	Тригонометрические функции:	a			a
4.	Тригонометрические функции:					sin x
						sin x
	y = sin x, y = cos x,			y = tg x, y = ctg x, tg x =			, ctg x =
	y = sin x, y = cos x,			y = tg x, y = ctg x, tg x =		cos x	, ctg x =
						cos x

cos x . sin x

5.Обратные тригонометрические функции:


y = arcsin x,	y = arccos x,						y = arctg x, y = arcctgx
				π		;	π
( y = arcsin x ::= y −				2		;	(sin y = x);
				2			2
y = arccos x ::= (y [0; π]) (cos y = x);
y = arctg x ::=		−	π	;	π
y = arctg x ::=	y	−	2	;	2		(tg y = x);
			2		2

y= arcctgx ::= (y (0; π)) (ctg y = x) .

6.Гиперболические функции:

y = sh x (гиперболический синус), y = ch x (гиперболический косинус), y = th x (гиперболический тангенс),

y = cth x (гиперболический котангенс):

sh x =

ex −e−x

, ch x =

ex +e−x

th x =

sh x

, cth x =

ch x

sh x

Приложение 2

НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

Рациональная функция: y = Pn (x) , где Pn (x) −многочлен степени n:

P (x) = a xn + a xn−1 +... + a

n−1

x + a ;

a0 , a1,..., an−1, an R;

a0 ≠ 0 .

Частные случаи:

Линейная функция:

y = ax +b; a,b R; a ≠ 0.

Квадратичная функция:

y = ax2 +bx +c; a,b, c R; a ≠ 0.

Дробно-рациональная функция:

y =

Pn (x)

Qm (x)

где Pn (x), Qm (x) − многочлены степени n и m соответственно.

Частные случаи:

Дробно-линейная функция:

y = cxax++db ; a,b, c, d R; c ≠ 0.

Приложение 3

ТАБЛИЦА ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

y = f (x)

y = f (u(x))

1. (xα )′ = αxα−1

(uα )′ = αuα−1 u′

( x )′ =

( u )′ =

u′

2 x

′

= −

′

= −

u′

2. (ax )′ = ax ln a

2. (au )′ = au ln a u′

(ex )′ = ex

(eu )′ = eu u′

3. (loga x)′

(loga u)′ =

u′

x ln a

u ln a

(ln x)′

(ln u)′

u′

4. (sin x)′ = cos x

(sin u)′ = cos u u′

5. (cos x)′ = −sin x

(cos u)′ = −sin u u′

′

6. (tg x)

= cos2 x

(tg u)

= cos2 u u

′

7. (ctg x)

= −sin

2 x

(ctg u)

= −sin2 u u

8. (arcsin x)′ =

(arcsin u)′ =

u′

1−u2

1− x2

9. (arccos x)′ = −

(arccos u)′ = −

u′

1− x2

1−u2

10. (arctg x)′ =

10. (arctg u)′

′

1+ x2

1+u2

11. (arcctgx)′ = −

11. (arcctgu)′ = −

u′

1+ x2

1+u2

12. (sh x)′ = ch x

12. (sh u)′ = ch u u′

13. (ch x)′ = sh x

13. (ch u)′ = sh u u′

′

14. (th x)

= ch2 x

14. (th u)

= ch2 u u

′

15. (cth x)

= − sh

2 x

15. (cth u)

= − sh2 u u

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.05.20151.09 Mб40kursovaya.rtf
#
21.11.20186.65 Mб3kursovaya_-_2913 (2).doc
#
20.03.201676.49 Кб10Kursovaya_bts-31.docx-10938624.docx
#
20.03.2016689.43 Кб98kursovaya_rabota.docx
#
14.09.2019113.96 Кб6kursovik.docx
#
20.03.20161.26 Mб13k_Fomin.pdf
#
22.05.2015317.42 Кб12k_Glazkov1.pdf
#
22.05.2015691.24 Кб21k_Jukov.pdf
#
22.05.201570.4 Кб14K_r_Skrebnev.docx
#
22.05.2015336.38 Кб16lab_aKiTp.doc
#
22.05.201542.59 Mб55Language_Leader_Intermediate_WB.pdf