Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тамбовский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

k_Fomin

.pdf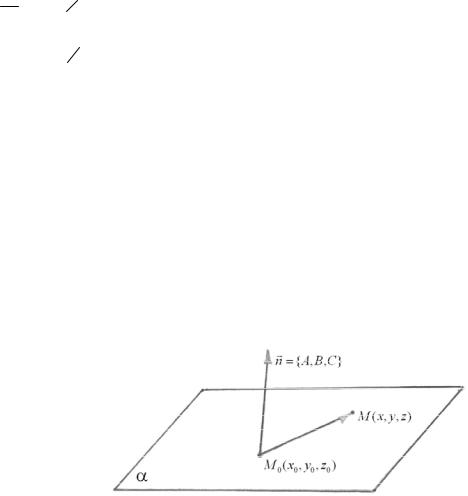

Скачиваний:

Добавлен:

20.03.2016

Размер:

1.26 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

	r	r
	(3b)(−8c) = −504 ;
г)	r	−2; 7},	r	{1;	−3; 2}
г)	b ={1;	−2; 7},	c =	{1;	−3; 2}

11 ≠ −−23 ≠ 72 br|| cr ; rr

bc = 21 (см. п. в) ); rr r r bc = 21 ≠ 0 b c ;

д)	r	r	r	rrr	;
д)	(5a)(4b)(3c) = 60abc				;
	rrr		(см. п. а) )
	abc =18		(см. п. а) )				r	r
	r	r	r			векторы	r	r	не компланарны.
	(5a)(4b)(3c) =1080 ≠ 0					векторы	5a ,	4b , 3c	не компланарны.

Задача 2.3 решена.

2.4. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ

Пусть в пространствеrзадана ДПСК и α − некоторая плоскость.

Нормальный вектор n плоскости α :: = любой ненулевой вектор, перпендикулярный к этой плоскости.

Пусть плоскость α проходит через данную точку M0 (x0 , y0 , z0 ) и имеет заданный нормальный вектор n ={A, B,C}

(рис. 29).

Рис. 29

Найдем уравнение плоскости α .				r uuuuuur	r uuuuuur
				r uuuuuur	r uuuuuur
Пусть M (x, y, z) − переменная точка с текущими координатами x , y , z . Тогда M α n M0 M					n M0 M	= 0 ;
r		uuuuur	− x0 , y − y0 , z − z0};
n ={A, B,C};		M0 M ={x	− x0 , y − y0 , z − z0};
r	uuuuuur
n	M0 M = A(x − x0 ) + B( y − y0 ) +C(z − z0 ) .
r uuuuuur
Соотношение n M0 M = 0 принимает вид
			A(x − x0 ) + B( y − y0 ) +C(z − z0 ) = 0 .			(58)
Итак, уравнение плоскости α , проходящей через данную точку			M0 (x0 , y0 , z0 ) и имеющий заданный нормальный вектор
r
n ={A, B,C} задается соотношением (58).
Уравнение (58) можно записать в виде
			Ax + By +Cz + D = 0 ,			(59)
где D = −Ax0 − By0 −Cz0 .
Уравнение (59) называется общим уравнением плоскости. Коэффициенты при x , y , z				в этом уравнении являются ко-
ординатами нормального вектора данной плоскости.
Выведем уравнение плоскости α , проходящей через три данные точки M1(x1, y1, z1 ) ,				M2 (x2 , y2 , z2 ) , M3 (x3 , y3 , z3 ) , не
лежащие на одной прямой (рис. 30).

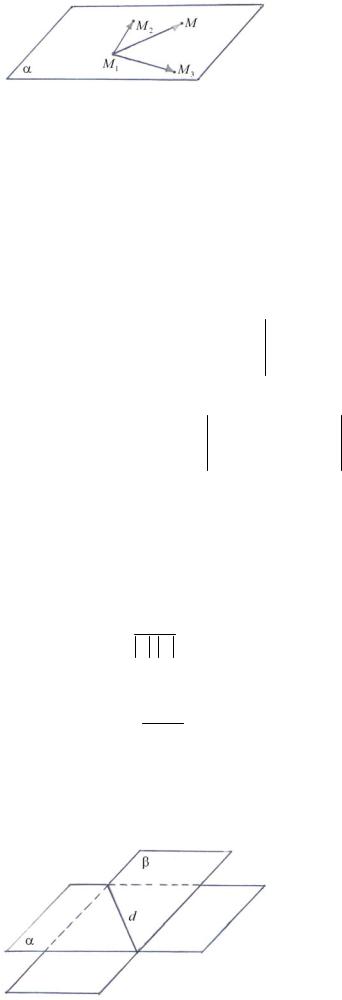
Рис. 30

uuuur uuuuuur

Пусть M (x, y, z) − переменная точка с текущими координатами x , y , z . Тогда M α векторы M1M , M1M2 , uuuuuuur

M1M3 компланарны

					uuuur	uuuuuuur	uuuuuuur
Имеем:					M1M	M1M2	M1M3	= 0 .	(60)
Имеем:	uuuuur				z − z1};
	uuuuur			, y − y1,
	M1M ={x − x1			, y − y1,
	uuuuuuur	={x2	− x1	, y2 − y1	, z2 − z1};
	M1M2	={x2	− x1	, y2 − y1	, z2 − z1};
	uuuuuuur	={x3	− x1	, y3 − y1	, z3 − z1};
	M1M3	={x3	− x1	, y3 − y1	, z3 − z1};

uuuuur uuuuuuur uuuuuuur		x − x1
uuuuur uuuuuuur uuuuuuur		x − x1
M1M M1M2 M1M3	=	x2 − x1
		x3 − x1

Соотношение (60) принимает вид

y − y1 y2 − y1 y2 − y1

z − z1 z2 − z1 . z3 − z1

x − x1 x2 − x1 x3 − x1

y − y1 y2 − y1 y3 − y1

z − z1

z2 − z1 = 0 . (61) z3 − z1

Итак, уравнение искомой плоскости α имеет вид (61).

Определитель в левой части (61) нужно раскрывать по элементам первой строки. В результате уравнение (61) сведется к виду (59).

Угол между двумя плоскостями определяется как угол между нормальными векторами этих плоскостей: пусть

α : A1x + B1 y +C1z + D1 = 0 ; : A2 x + B2 y +C2 z + D2 = 0 ,

ψ − угол между плоскостями α и β , тогда

ruu

cos ψ = uurn1 nuur2 , n1 n2

	uur	={A1, B1,C1};	uur	={A2 , B2 ,C2}. Следовательно,
где	n1	={A1, B1,C1};	n2	={A2 , B2 ,C2}. Следовательно,
					ruu
					n1 n2
				ψ = arccos	uur	uur	.
					n1	n2

Пусть в пространстве дана некоторая прямая d . Рассмотрим две различные плоскости α и β , пересекающиеся по пря-

мой d (рис. 31).

Пусть α и β заданы уравнениями

α : A1x + B1 y +C1z + D1 = 0 ; β : A2 x + B2 y +C2 z + D2 = 0 .

Рис. 31

Тогда прямую d можно задать системой двух уравнений

		A x + B y +C z + D = 0 ;					(62)
		1	1	1	1	0 .	(62)
		A2 x + B2 y +C2 z + D2 =				0 .
Уравнения (62) называются общими уравнениями прямой d .
Направляющий вектор	r	прямой d :: = любой ненулевой вектор, параллельный данной прямой.
Направляющий вектор	a
Выведем уравнения прямой d , проходящей через данную точку M0 (x0 , y0 , z0 )				и имеющей заданный направляющий
r
вектор a ={l, m, n} (рис. 32).

Рис. 32

Пусть M (x, y, z) − переменная точка с текущими координатами x , y , z . Тогда

		M d M0M \|\|				ar .			(63)
	uuuuuur	={x − x0 , y − y0 , z − z0}. В силу первого признака коллинеарности векторов
Заметим, что	M0 M
		M0M \|\| ar	x − x0	=	y − y0	=	z − z0	.	(64)
		M0M \|\| ar	l	=	m	=		.	(64)
			l		m		n

В силу (63), (64) уравнения прямой d , проходящий через данную точку M0 (x0 , y0 , z0 ) и имеющей заданный направ-
r
ляющий вектор a ={l, m, n}, записываются в виде
	x − x0	=	y − y0	=	z − z0	.	(65)
	l	=	m	=		.	(65)
	l		m		n
Уравнения (65) называются каноническими уравнениями прямой d .
Найдем уравнения прямой d , проходящей через две данные точки M1(x1, y1, z1 ) и M2 (x2 , y2 , z2 )							(рис. 33).

Рис. 33

В качестве направляющего вектора прямой d	можно взять вектор	uuuuuur				={x				− x , y			− y , z					− z		}:	r	uuuuuur			. Тогда,
В качестве направляющего вектора прямой d	можно взять вектор	M		M	2	={x				− x , y		2	− y , z				2	− z		}:	a	= M	M	2	. Тогда,
		1			2			2			1	2				1	2		1			1		2
беря в качестве M0 точку M1 и используя (65), получаем уравнения прямой d :
			x − x1				=		y − y1			=		z − z1				.							(66)
			x − x				=					=						.							(66)
			x − x					y		2	− y			z	2	− z
				2		1				2	1				2		1

Уравнения (66) называются каноническими уравнениями прямой, проходящей через две данные точки M1(x1, y1, z1 ) и

M2 (x2 , y2 , z2 ) .

Задача 2.4. По координатам вершин пирамиды A1 A2 A3 A4 найти:

а) длины ребер A1 A2 и A1 A3 ;

б) угол между ребрами A1 A2 и A1 A3 ;

в) площадь грани A1 A2 A3 ; г) объем пирамиды;

д) уравнения прямых A1 A2 и A1 A3 ;

е) уравнения плоскостей A1 A2 A3 и A1 A2 A4 ;

ж)

угол между плоскостями A1 A2 A3

и A1 A2 A4 .

A1(6;1; 4) ; A2 (2; −2; −5) ;

A3 (7;1; 3) ;

A4 (1; −3; 7) .

Решение.

а)

Используя формулу для вычисления расстояния между двумя точками A(x1, y1, z1)

и B(x2 , y2 , z2 ) пространства

= (x − x

+(y

− y

+(z

− z )2

получаем:

A A

(2 −6)2 +(−2 −1)2

+(−5 − 4)2

16 +9 +81 =

106 ;

A A

= (7 −6)2 +(1−1)2 +(3 − 4)2 = 1+ 0 +1 = 2 .

Итак,

A1 A2

106 ,

A1 A3

= 2 .

uuuur

Угол ϕ между ребрами A1 A2 и A1 A3

б)

равен углу между векторами A1 A2 и

A1 A3 , следовательно,

uuuur

uuuuur

cos ϕ =

A1 A2

A1 A3

uuuuur

A1 A2

A1 A3

uuuuur

{2 −6; −2 −1; −5 − 4},

uuuuur

={−4; −3; −9};

Имеем:

A1 A2 =

A1 A2

uuuuur

={7 −6;1−1;3 −4},

uuuur

−1};

A1 A3

A1 A3 ={1;0;

uuuuur

A1 A2

A1 A3

= −4 1+ (−3)

0 + (−9) (−1) = −4 + 0 +9 = 5 ,

uuuur

uuuuur

A1 A2

A1 A3

= 5 ;

uuuuur

A1 A2

106 ,

A1 A3

(см. п. а) );

cos ϕ =

;

106

ϕ = arccos

106

в)

Площадь грани A1 A2 A3 равна площади ∆ A1 A2 A3 , а площадь ∆ A1 A2 A3

− это площадь треугольника, построенного на

uuuuur

векторах A1 A2

, A1 A3

. Следовательно,

uuuuur

A A A

A A

× A A

uuuuur

uuuur

={1;0; −1} (см. п. б) );

Имеем:

A1 A2 ={−4; −3; −9}, A1 A3

uuuuur

−3

−9

−4

−9

A A

× A A

−4 −3 −9

= i

− j

−1

−4

−3

{3;

−13;3},

= 3i −13 j

uuuur

uuuuur

{3; −13;3};

A1 A2

× A1 A3

uuuuur

32 +(−13)2 +32

9 +169 +9 =

187 ,

A A × A A

uuuuur

A1 A2

× A1 A3

187 ;

SA A A

187

г)

Объем пирамиды A1 A2 A3 A4

– это объем пирамиды, построенной на векторах A1 A2 ,

A1 A3 , A1 A4 , следовательно,

1 uuuuur uuuuur uuuuur

Vпир = 6 A1 A2 A1 A3 A1 A4 .

	uuuuur	={−4; −3; −9},	uuuuur	={1;0; −1},	uuuuur	={−5; −4;3};
Имеем:	A1 A2	={−4; −3; −9},	A1 A3	={1;0; −1},	A1 A4	={−5; −4;3};

+1 (−4) (−9) −(−9) 0 (−5) −(−3) 1 3 −(−1) (−4) (−4) =

= 0 −15 +36 −0 +9 +16 = 46 ,				uuuuur	uuuuur	uuuuur
uuuuur	uuuuur	uuuuur		uuuuur	uuuuur	uuuuur
A1 A2	A1 A3	A1 A4	= 46 ;	A1 A2	A1 A3	A1 A4	=	46	= 46 ;

Vпир = 16 46 = 233 = 7 23 ,

Vпир = 7 23 .

д) Используя канонические уравнения прямой, проходящей через две данные точки M1(x1, y1, z1 ) и M2 (x2 , y2 , z2 ) :

x − x1		=	y − y1			=	z − z1			,

x	− x		y	2	− y		z	2	− z
2	1				1				1

получаем:

(A1 A2 ) : 2x −−66 = −y2−−11 = −z5−−44 , (A1 A2 ) : x−−46 = y−−31 = z−−94 ;

(A A ) :

x −6

y −1

z −4

−6

1−1

3 −4

−4 −3 −9

(A A ) :

x −6

y −1

z −4

A A A A A A =

0 −1

−1

= −4 0 3 +(−3) (−1) (−5) +

uuuuur

−5

−4 3

плоскости, проходящей через три данные точки M1(x1, y1, z1 ) ; M2 (x2 , y2 , z2 ) ; M3 (x3 , y3 , z3 ) :

е)

Используя

уравнение

x − x1 x2 − x1 x3 − x1

получаем:

y − y1 y2 − y1 y3 − y1

z − z1

z2 − z1 = 0 , z3 − z1

(A1 A2 A3 ) :

x −6

y −1

z −4

= 0 ,

2 −6 −2 −1 −5 −4

7 −6

1−1

3 −4

x −6

y −1

z −4

= (x −6)

−3

−9

−( y −1)

−4 −9

−4

−3

−9

−1

1 −1

+(z −4)

−4 −3

= 3 (x −6) −13 ( y −1) +3 (z − 4) =

= 3x −13y +3z −18 +13 −12 = 3x −13y +3z −17 ,

(A1 A2 A3 ) : 3x −13y +3z −17 = 0 ;

(A1 A2 A4 ) :

x −6

y −1

z −4

= 0 ,

−4

−3

−9

−5

−4

x −6

y −1

z −4

= (x −6)

−3

−9

−( y −1)

−4

−9

−4

−3

−9

−5

−4

−5

−4

−3

= −45(x −6) +57( y −1) +(z − 4) =

+(z −4)

−5

−4

= −45x +57 y + z + 270 −57 − 4 = −45x +57 y + z + 209 ,

(A1 A2 A4 )

: −45x +57 y + z + 209 = 0 .

ж) Из уравнений плоскостей (A1 A2 A3 ) и (A1 A2 A4 ), найденных в п. е), следует, что нормальные векторы этих плоскостей имеют вид:

uur

={−45;57;1}.

n1 ={3; −13;3} и

Тогда косинус угла ψ между плоскостями (A1 A2 A3 ) и (A1 A2 A4 ) находится по формуле

ruu

n1 n2

cos ψ =

uur

Имеем:

ruu

n1 n2 = 3

(−45)

+ (−13) 57 +3 1 = −135 −741+3 = −873 ,

ruu

uur

n1 n2 = −873 ;

uur

+(−13)2 +32

187 ,

187 ;

uur

= (−45)2

+572 +12 =

2025 +3249 +1 =

5275 = 5

211 ,

uur

= 5

211 ;

−873

;

873

;

cos ψ =

ψ = arccos

−

187

5 211

187

211

873

ψ = π−arccos

187 5 211

Задача 2.4 решена.

Контрольная работа 3

ВВЕДЕНИЕ В АНАЛИЗ

3.1. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ

Говорят, что на плоскости определена полярная система координат, если заданы

1)точка O , называемая полюсом;

2)исходящий из точки O луч Oρ , называемый полярной осью;

3)единица измерения длин.

Пусть на плоскости дана полярная система координат и M − произвольная точка плоскости, отличная от полюса O

(рис. 34).

Рис. 34

Тогда положение точки M однозначно определяется двумя числами:

а)	углом наклона ϕ	вектора		uuuur	к полярной оси, называемым полярным углом точки M	(по определению
				OM
0 ≤ ϕ < 2π );		uuuur
б)	длиной ρ вектора		(расстоянием от точки M до полюса), называемой полярным радиусом точки M .
		OM

Числа ϕ и ρ называются полярными координатами точки M : M (ϕ,ρ).

Для полюса ρ = 0 , а ϕ не определено.

Еще раз подчеркнем, что, по определению, 0 ≤ ϕ < 2π , ρ ≥ 0 . Замечание. В некоторых случаях удобно считать, что −π < ϕ ≤ π.

Пусть на плоскости задана полярная система координат. Введем на этой плоскости ДПСК, поместив ее начало в полюс и взяв полярную ось Oρ в качестве положительной полуоси Ox (единица измерения длин в ДПСК та же, что и в полярной

системе координат) (рис. 35).

Рис. 35

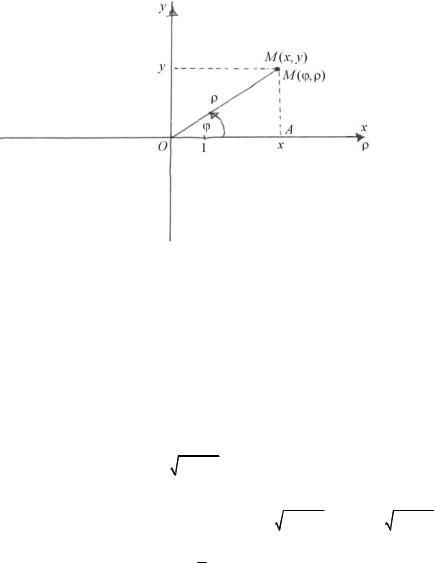
Тогда положение произвольной точки M этой плоскости можно задавать как полярными, так и декартовыми прямоугольными координатами: M (ϕ,ρ) или M (x, y).

Из прямоугольного треугольника ∆OAM видно, что декартовы прямоугольные координаты точки выражаются через ее полярные координаты по формулам:

x = ρcos ϕ ; y = ρsin ϕ.

Из того же треугольника следуют формулы, выражающие полярные координаты точки через ее декартовы прямоугольные координаты:

ρ = x2 + y2 ;
cos ϕ =	x	; sin ϕ =	y	;	(67)
cos ϕ =	x2 + y2	; sin ϕ =	x2 + y2	;	(67)
	x2 + y2		x2 + y2

tg ϕ = xy .

Угол ϕ определяется из соотношений (67), при этом следует помнить, что, по определению, 0 ≤ ϕ < 2π .

Задача 3.1. Требуется:

а) построить по точкам график функции ρ = ρ(ϕ) в полярной системе координат (значения функции вычислять в точ-

ках ϕk = π8k );

б) найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ox − с полярной осью;

в) определить вид кривой.

ρ = 3sin 2ϕ .

Решение.

а) Найдем область определения данной функции, исходя из того, что, по определению, ρ ≥ 0 , 0 ≤ ϕ < 2π :

	3sin 2ϕ ≥ 0 ;		sin 2ϕ ≥ 0 ;
	;		0 ≤ ϕ ≤		π
0 ≤ 2ϕ ≤ π					2
	2π ≤ 2ϕ ≤	3π			3π

	.			π ≤ ϕ ≤
					2

		π		3π
Итак,	D(ρ) = 0;		π;		.
		2		2

Заполним таблицу вида

ϕ	0		π	π	3π				π	π	π+				π		π+	π	π+			3π		3π
ϕ	0		8	4				8	2	π	π+				8		π+	4	π+					2
			8	4				8	2						8			4				8		2
2ϕ	0		π	π			3π		π	2π	2π+					π	2π+	π	2π+				3π	3π
2ϕ	0		4	2				4	π	2π	2π+				4		2π+	2	2π+			4		3π
			4	2				4							4			2				4
sin 2ϕ	0		2	1				2	0	0			2				1				2			0
sin 2ϕ	0		2	1				2	0	0		2					1		2					0
			2					2				2							2
ρ	0	3	2	3		3		2	0	0		3		2			3			3		2		0
ρ	0		2	3				2	0	0		2					3		2					0
			2					2				2							2

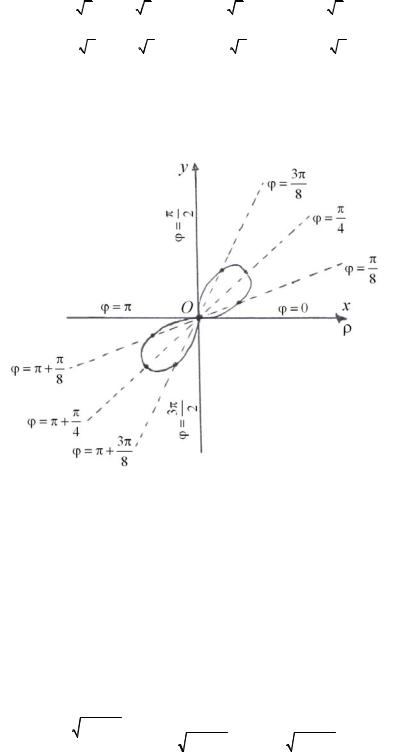
Отмечая полученные точки (ϕk ;ρk ) в полярной системе координат и соединяя их плавной линией, получаем график функции ρ = 3sin 2ϕ (рис. 36).

Рис. 36

б) Найдем уравнение кривой в прямоугольной системе координат:

ρ = 3sin 2ϕ .

Используя формулу для синуса двойного аргумента, получаем:

ρ = 6sin ϕcos ϕ .
Учитывая, что
ρ = x2 + y2 ; sin ϕ =	y	; cos ϕ =	x	,
ρ = x2 + y2 ; sin ϕ =	x2 + y2	; cos ϕ =	x2 + y2	,
	x2 + y2		x2 + y2

имеем:

	x2 + y2 =	6xy
	x2 + y2 =	x2 + y2
		x2 + y2

или

(x2 + y2 ) x2 + y2 −6xy = 0 .

в) Кривая представляет собой двухлепестковую розу.

Задача 3.1 решена.

3.2. ПРЕДЕЛЫ

Пусть x0 R .

Дельта-окрестность Oδ (x0 ) точки x0 :: = интервал с центром в точке x0 радиуса δ : Oδ (x0 ) = (x0 −δ, x0 +δ) (рис. 37).

Рис. 37

Таким образом, Oδ (x0 ) ={x R : x − x0 < δ}.

Проколотая дельта окрестность O&δ (x0 ) точки x0 :: = множество вида O&δ (x0 ) = Oδ (x0 ) \ {x0}, т.е. множество, полу-

чаемое из Oδ (x0 ) удалением точки x0 .

Таким образом, O&δ (x0 ) ={x R : 0 < x − x0 < δ}. Рассмотрим некоторое множество M R .

Точка x0 R называется предельной точкой множества M , если в любой сколь угодно малой δ-окрестности точки x0 найдется хотя бы одна точка, принадлежащая множеству M , отличная от точки x0 :

Oδ (x0 ) x O&δ (x0 ) x M .

Пример. Пусть M =[2;5) (рис. 38).

Рис. 38

Из рисунка видно, что x0 = 2 , x1 = 3 , x2 = 5 − предельные точки множества M , при этом x0 , x1 M , а x2 M , т.е. предельная точка множества может принадлежать, но может и не принадлежать этому множеству.

Замечание. Если x0 − предельная точка множества M , то в любой сколь угодно малой δ-окрестности этой точки найдется бесконечное число точек, отличных от точки x0 , принадлежащих множеству M (рис. 39).

Рис. 39

Пусть функция y = f (x) задана на своей области определения D( y) и x0 − предельная точка множества D( y) .

Число А называется пределом функции f (x) в точке x0 (или при x стремящемся к x0 ), если для любого сколь угодно малого положительного числа ε найдется положительное число δ , определяемое в зависимости от взятого числа ε , такое, что для любого x D( y) , такого, что 0 < x − x0 < δ , выполняется неравенство f (x) − A < ε .

Обозначение:

lim f (x) = A .

(68)

Таким образом, соотношение (68) означает, по определению, следующее:

x→x0

ε > 0 δ = δ(ε) > 0

x D( y) : 0 <

x − x0

< δ

f (x) − A

< ε .

Условие 0 <

x − x

< δ означает, что x O&

(x ) . Аналогично, условие

f (x) − A

< ε означает, что

f (x) O (A) . В свя-

зи с этим можно дать геометрическое определение предела функции в точке.

Точка

называется

пределом

функции

f (x)

точке

x0 ,

если

для

Oε (A)

O (x ), δ = δ(ε)

x D( y) : x O&

(x ) f (x) O (A) (рис. 40).

Рис. 40

При вычислении пределов функций применяют основную теорему о пределах:

Теорема.				Пусть функции u = u(x) , v = v(x) имеют в точке x0 конечные пределы. Тогда сумма, разность, произведе-
ние и частное этих функций тоже имеют конечные пределы в точке x0 и справедливы формулы:
1)	lim [u(x) +v(x)]= lim u(x) + lim v(x) ;
	x→x0			x→x0	x→x0
2)	lim [u(x) −v(x)]= lim u(x) − lim v(x) ;
	x→x0			x→x0	x→x0
3)	lim [u(x) v(x)]= lim u(x) lim v(x) ;
	x→x0			x→x0	x→x0
		u(x)		lim u(x)
4)	lim	u(x)	=	x→x0
4)	lim		=	lim v(x)
	x→x0	v(x)		lim v(x)
				x→x0
(в случае частного предполагается, что						lim v(x) ≠ 0 ).
						x→x0
Если f (x) ≡ C для x D( y)					и x0	− предельная точка множества D( y) , то
5)	lim C = C ,
	x→x0
т.е. предел постоянной равен этой постоянной.
Из свойств 3), 5) следует, что
6)	lim [Cu(x)]= C lim u(x) ,
	x→x0			x→x0

т.е. постоянную можно выносить за знак предела.

В качестве предельной точки x0 множества D( y) может выступать бесконечно удаленная точка ∞ .

Число А называется пределом функции f (x) при x → ∞ , если для любого сколь угодно малого положительного числа ε найдется положительное число ∆ , определяемое в зависимости от взятого числа ε , такое, что для любого x D( y) , такого что x > ∆ , выполняется неравенство f (x) − A < ε .

Обозначение:

	lim f (x) = A .
	x→∞
Многочлен n-й степени одной переменной x :: = выражение вида
P(x) = a xn + a xn−1 +... + a		n−1	x + a	,
0	1	n−1		n

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.05.20151.09 Mб40kursovaya.rtf
#
21.11.20186.65 Mб3kursovaya_-_2913 (2).doc
#
20.03.201676.49 Кб10Kursovaya_bts-31.docx-10938624.docx
#
20.03.2016689.43 Кб98kursovaya_rabota.docx
#
14.09.2019113.96 Кб6kursovik.docx
#
20.03.20161.26 Mб13k_Fomin.pdf
#
22.05.2015317.42 Кб12k_Glazkov1.pdf
#
22.05.2015691.24 Кб21k_Jukov.pdf
#
22.05.201570.4 Кб14K_r_Skrebnev.docx
#
22.05.2015336.38 Кб16lab_aKiTp.doc
#
22.05.201542.59 Mб55Language_Leader_Intermediate_WB.pdf