
k_Fomin
.pdf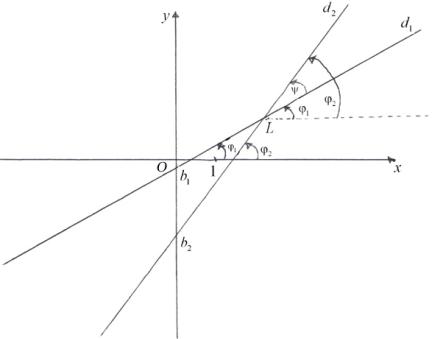
Прямая d проходит через точку M1 (x1, y1 ) и имеет угловой коэффициент вида (32), следовательно, в силу (31) уравнение d имеет вид
y − y = |
y2 − y1 |
(x − x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 − x1 |
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y − y1 |
= |
x − x1 |
. |
(33) |
||||
|
|
|
|
|
|
|||||||
|
|
|
|
y |
2 |
− y |
|
x |
− x |
|
||
|
|
|
|
|
|
1 |
2 |
1 |
|
|
||
Таким образом, уравнение прямой, проходящей через две данные точки M1 (x1, y1 ), |
M2 (x2 , y2 ), записывается в виде (33). |
|||||||||||
Рассмотрим на плоскости, снабженной ДПСК, две прямые d1 : y = k1x + b1 и d2 : y = k2 x + b2 (рис. 3). |
|
|||||||||||
Пусть ψ − угол наклона прямой d2 к прямой d1 , т.е. угол, на который нужно повернуть прямую d1 |
вокруг точки L пе- |
|||||||||||
ресечения этих прямых, чтобы она совпала с прямой d2 . Из чертежа видно, |
что ψ = ϕ2 −ϕ1 . Применяя известную формулу |
||||||
тригонометрии |
|
|
|
|
|
|
|
tg (α −β)= |
tg α − tg β |
, |
|
|
|||
|
|
|
|
||||
|
|
|
1+ tg αtg β |
|
|
||
получаем |
|
|
|
|
|
|
|
tg ψ = tg (ϕ |
2 |
−ϕ )= |
tg ϕ2 − tg ϕ1 |
|
, |
||
|
|
||||||
|
1 |
1+ tg ϕ1 tg ϕ2 |
|
|
|||
|
|
|
|
|
|||
Рис. 3
или с учетом того, что tg ϕ2 = k2 , tg ϕ1 = k1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg ψ = |
k2 −k1 |
. |
(34) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1+ k k |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Таким образом, тангенс угла наклона прямой d2 : y = k2 x + b2 |
к прямой d1 : y = k1x + b1 вычисляется по формуле (34). |
|
||||||||||
Анализ формулы (34) приводит к следующим утверждениям: |
|
|
|
|
|
|
|
|||||
• признак параллельности двух прямых: |
|
|
|
|
|
|
|
|
|
|
|
|
d1 || d2 k1 = k2 ; |
|
|
|
|
||||||||
• признак перпендикулярности двух прямых: |
|
|
|
|
|
|
|
|
|
|
|
|
d1 d2 1+ k1k2 = 0 |
|
|
|
|
||||||||
или |
|
|
|
|
|
|
1 |
|
|
|
|
|
d |
d |
2 |
k |
2 |
= − |
. |
|
|
|
|
||
|
|
|
|
|
||||||||
1 |
|
|
|
|
k1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Задача 2.1. Даны координаты вершин треугольника ABC . Найти:
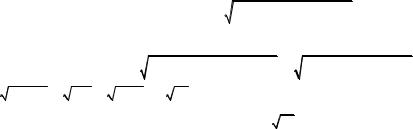
а) |
длину стороны AB ; |
б) |
уравнения сторон AB и BC и их угловые коэффициенты; |
в) |
угол B ; |
г) |
уравнение высоты CD и ее длину; |
д) |
уравнение медианы AE и координаты точки K пересечения этой медианы с высотой CD ; |
е) |
уравнение прямой, проходящей через точку K параллельно стороне AB ; |
ж) координаты точки M , расположенной симметрично точке A относительно прямой (CD) :
A(1; −6) , B(3;4) , С(−3;3) .
Решение.
а) Найдем длину стороны AB . Используя формулу для вычисления расстояния между точками M1 (x1, y1 ) и
M2 (x2 , y2 )
|
|
|
|
M |
M |
2 |
|
= |
(x − x )2 +(y |
2 |
− y )2 |
, |
|||
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
2 |
1 |
|
1 |
|
|||
получаем |
|
|
|
|
|
|
|
|
|
|
|
||||
|
AB |
|
= (xB − xA )2 +(yB − yA )2 = (3 −1)2 +(4 −(−6))2 = |
||||||||||||
|
|
||||||||||||||
= 4 +100 = 104 = 4 26 = 2 26 , |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
AB |
|
= 2 |
26 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) Найдем уравнения сторон AB и BC и их угловые коэффициенты. Используя уравнение прямой, проходящей через две данные точки M1 (x1, y1 ), M2 (x2 , y2 ):
|
|
|
|
|
|
|
|
|
|
|
|
|
y − y1 |
= |
|
x − x1 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
− y |
|
|
|
|
x |
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
( AB) : |
|
y − yA |
= |
|
x − xA |
; |
|
|
y −(−6) |
|
= |
x −1 |
|
; |
|
y +6 |
= |
x −1 |
; |
|||||||||||||||||||||||
|
|
|
|
|
|
yB − yA |
|
xB − xA |
|
4 −(−6) |
|
|
|
3 −1 |
|
10 |
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y + 6 = 5x −5 ; |
y = 5x −11 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Итак, AB : y = 5x −11 , |
1 ≤ x ≤ 3 , следовательно, |
kAB = 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Аналогично, |
|
|
|
|
y − yB |
|
|
x − xB |
|
|
|
|
y −4 |
|
|
|
x −3 |
|
|
|
|
y −4 |
|
|
x −3 |
|
|
||||||||||||||||||||
|
|
|
|
|
(BC) : |
|
= |
|
; |
|
|
|
= |
|
|
; |
|
= |
; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y − y |
B |
|
|
x − x |
B |
|
|
3 −4 |
|
−3 −3 |
|
|
−1 |
|
|
|
−6 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
C |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
y −4 = |
|
1 |
x − |
|
1 |
; |
|
y = |
|
1 |
x + |
7 |
. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
2 |
|
6 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Итак, BC : y = |
1 |
x + |
7 |
, |
−3 ≤ x ≤ 3 , следовательно, kBC = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
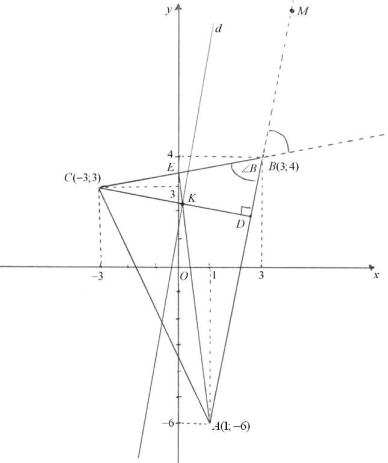
в) Найдем угол В. Изобразим треугольник ∆АВС на чертеже (рис. 4).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из чертежа видно, что B равен углу наклона прямой (AB) |
|
к прямой (BC) . Используя формулу для вычисления тан- |
||||||||||||||||||||||||||||||||||||||
генса угла наклона прямой d2 : y = k2 x + b2 к прямой d1 : y = k1x + b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
tg ψ = |
|
k2 −k1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ k k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
kAB −kBC |
|
|
|
|
5 − |
|
|
|
30 −1 |
|
29 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
tg B = |
|
|
= |
6 |
|
|
= |
= |
, |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
+ kBC kAB |
|
|
|
6 + |
5 |
|
11 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1+ |
|
5 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
tg B = |
|
29 |
, следовательно, B = arctg |
29 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
г) |
Найдем уравнение высоты CD и ее длину. Прямая (CD) |
перпендикулярна прямой (AB) . Следовательно, по при- |
||||||||||||||||||||||||||||||||||||||
знаку перпендикулярности двух прямых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
k |
CD |
|
= − |
1 |
|
, k |
CD |
|
= − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
kAB |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Прямая (CD) проходит через точку С(−3;3) |
и имеет угловой коэффициент |
k |
|
= − |
1 |
. Используя уравнение прямой, прохо- |
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CD |
|
5 |
|
|
|
|
|
||
дящей через данную точку M0 (x0 , y0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и имеющей заданный угловой коэффициент k : |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y − y0 = k (x − x0 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(CD) : y − y = k |
CD |
(x − x |
|
); y −3 = − |
1 |
|
(x −(−3)); y −3 = − |
1 |
x − |
3 |
; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
C |
|
|
|
|
C |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y = − |
1 |
x + |
12 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Итак, CD : y = − |
1 |
x + |
12 |
|
−3 ≤ x ≤ |
67 |
|
67 |
|
||
|
|
|
, |
|
xD = |
26 |
, см. ниже . Найдем длину высоты CD . Для этого найдем координаты точ- |
||||
5 |
5 |
26 |
|||||||||
|
|
|
|
|
|
||||||
ки D = (AB) ∩(CD) . Так как точка D принадлежит прямым (AB) и (CD) , то ее координаты удов-
летворяют уравнениям этих прямых. Следовательно, для нахождения координат точки D нужно решить систему уравнений
y = 5x −11;
y = −1 x +12 .
5 5
Получаем
5x −11 = − |
1 |
x + |
12 |
; 25x −55 = −x +12 ; 26x = 67 ; x = |
67 |
; |
||
5 |
|
5 |
26 |
|||||
|
|
|
|
|||||
y = 5x −11 ; y = 5 6726 −11 = 4926 .
Итак, D 67 , 49 . Тогда
26 26
|
|
|
|
|
CD |
|
= (x |
|
− x )2 |
+(y |
|
|
|
− y )2 = |
|
|
|
67 |
−(−3) 2 |
+ |
|
49 |
−3 2 = |
|
21866 |
; |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
D |
D |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CD |
|
= |
|
|
21866 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
д) Найдем уравнение медианы |
AE и координаты точки |
K |
|
|
|
|
пересечения этой медианы с высотой CD . По условию |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точка E является серединой отрезка |
BC . Используя формулы для нахождения координат точки M0 (x0 , y0 ), являющейся |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
серединой отрезка M1M2 , где M1 (x1, y1 ), M2 (x2 , y2 ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
= |
x1 + x2 |
|
|
; y |
= |
|
|
y1 + y2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xE |
= |
|
|
xB + xC |
|
|
; yE = |
yB + yC |
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
xE = |
3 +(−3) |
= 0 ; yE = |
4 +3 |
= |
|
7 |
; |
|
E 0; |
7 |
. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Используя уравнение прямой, проходящей через две данные точки, получаем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(AE) : |
|
y − yA |
= |
|
x − xA |
; |
|
y −(−6) |
= |
|
x −1 |
; |
|
|
y +6 |
= −x +1 ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
yE − yA |
xE − xA |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 −1 |
|
|
19 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 − |
(−6) |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y +6 = − |
19 |
x + |
19 |
; |
|
y |
|
= − |
|
19 |
x |
+ |
|
7 |
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, AE : y = − |
19 |
x + |
7 |
, 0 ≤ x ≤1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем координаты точки K = (AE) ∩(CD) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = − |
19 |
x + |
|
7 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = − |
|
|
x + |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
− |
19 |
x + |
|
7 |
= − |
1 |
x + |
|
12 |
; 95x −35 = 2x −24 ; 93x =11 ; x = |
11 |
; |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
5 |
5 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
93 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y = − |
19 |
x + |
|
7 |
; y = − |
19 |
|
|
11 |
+ |
7 |
= |
|
442 |
|
; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
186 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
93 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||

11 442 K 93 ; 186 .
е) Найдем уравнение прямой, проходящей через точку K параллельно стороне AB . Обозначим эту прямую через d. По условию d || (AB). Следовательно, по признаку параллельности двух прямых
|
|
|
|
|
|
|
|
|
|
|
|
|
kd = kAB , kd = 5 . |
|
|
|
|
|
|
|
|
||||||||||||||||||
Прямая d проходит через точку K |
11 |
; |
442 |
и имеет угловой коэффициент kd |
= 5 . Используя уравнение прямой, проходя- |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
93 186 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
щей через данную точку и имеющей заданный угловой коэффициент, получаем |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
d : y − yK = kd (x − xK ); y − |
442 |
|
|
11 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= 5 x − |
|
; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
186 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
93 |
|||||||||
|
|
|
|
|
|
|
|
y − |
442 |
= 5x − |
55 |
; |
|
|
y = 5x + |
332 |
, |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
93 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
186 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
186 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d : y = 5x + |
|
332 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
186 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ж) Найдем координаты точки M , расположенной симметрично точке A относительно прямой (CD) . По условию точ- |
|||||||||||||||||||||||||||||||||||||||
ка D является серединой отрезка AM . Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
xD = |
xA + xM |
|
; |
|
|
yD |
= |
|
yA + yM |
, |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
xM = 2xD − xA ; yM = 2 yD − yA . |
|
|
|
||||||||||||||||||||||||||||
Учитывая, что D |
67 |
; |
49 |
(см. пункт г) ), получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
= 2 |
67 |
−1 = |
54 |
; |
|
y |
M |
= 2 |
49 |
|
−(−6) = |
127 |
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
M |
26 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
13 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |
|
127 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
; |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Задача 2.1 решена.
2.2. ЛИНИИ ВТОРОГО ПОРЯДКА
Линия (кривая) второго порядка :: = линия, которая в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением второй степени, т.е. уравнением вида
Ax2 + Bxy +Cy2 + Dx + Ey + F = 0 , |
(35) |
где A, B,C, D, E, F − некоторые фиксированные числа, называемые коэффициентами уравнения, причем хотя бы один из ко-
эффициентов A, B,C отличен от нуля, т.е. A2 + B2 +C2 ≠ 0 .
Уравнение (35) называется общим уравнением второй степени.
Примерами линий второго порядка являются окружность, эллипс, гипербола, парабола.
Окружность с центром в точке M0 радиуса r :: =геометрическое место точек плоскости, расстояние от которых до точки M0 равно r .
Пусть на плоскости задана ДПСК (рис. 5). Выведем уравнение окружности L с центром в точке M0 (x0 , y0 ) радиуса r .

Рис. 5
Пусть M (x, y)− переменная точка с текущими координатами x , y . Тогда M L M0 M = r . Используя формулу для вычисления расстояния между двумя точками плоскости, получаем
M0 M = (x − x0 )2 +(y − y0 )2 .
Следовательно,
M L (x − x0 )2 +(y − y0 )2 = r
или
(x − x |
)2 +(y − y |
0 |
)2 |
= r2 . |
(36) |
0 |
|
|
|
|
Таким образом, уравнение окружности с центром в точке M0 (x0 , y0 ) радиуса r задается формулой (36). В частности, уравнение окружности с центром в начале координат радиуса r имеет вид
x2 + y2 = r2 .
Уравнение (36) – это алгебраическое уравнение второй степени, следовательно, окружность есть линия второго порядка.
Эллипс :: =геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух фиксированных
точек F1 , |
F2 этой плоскости есть постоянная величина, равная 2a и эта постоянная больше расстояния между точками F1 и |
|||||||||||
F2 : 2a > 2c , где 2c = |
|
F1F2 |
|
, при этом, точки F1 и F2 |
называются фокусами эллипса. |
|
|
|
|
|||
|
|
|
|
|
|
|||||||
Рассмотрим на плоскости эллипс с фокусами F1 , |
F2 . Введем на этой плоскости ДПСК следующим образом: в качестве |
|||||||||||
оси абсцисс возьмем прямую (F1F2 ) , считая ее направленной от F1 к F2 , начало координат поместим в середине отрезка |
||||||||||||
F1F2 . При таком выборе ДПСК уравнение данного эллипса имеет вид |
|
|
|
|
||||||||
|
|
|
|
|
|
|
x2 |
|
+ |
y2 |
=1 , |
(37) |
|
|
|
|
|
|
|
a2 |
b2 |
||||
|
|
|
|
|
|
|
|
|
|
|||
где b = |
a2 −c2 (величина b является вещественным числом, ибо по определению эллипса 2a > 2c , т.е. |
a > c ). Заметим, |
||||||||||
что b < a . Уравнение (37) называется каноническим уравнением эллипса. Уравнение (37) – это алгебраическое уравнение второй степени, следовательно, эллипс есть линия второго порядка.
В уравнение (37) текущие координаты x , y переменой точки M (x, y), принадлежащей эллипсу, входят в четной степени, следовательно, эллипс симметричен относительно координатных осей Ox и Oy . Поэтому для построения эллипса
достаточно исследовать форму части эллипса, расположенной в первой координатной четверти, т.е. построить график функции
y = |
b |
a2 − x2 |
(38) |
|
a |
||||
|
|
|
при 0 ≤ x ≤ a (выражение (38) получено из формулы (37)), а затем с помощью зеркальных отражений графика относительно координатных осей восстановить форму эллипса в остальных координатных четвертях. В результате указанных операций получается, что эллипс имеет форму, изображенную на рис. 6.

Координатные оси Ox и Oy являются осями симметрии эллипса (оси симметрии эллипса называют обычно осями эллипса), а начало координат – центром симметрии эллипса (центр симметрии эллипса называют обычно центром эллипса). Таким образом, оси эллипса – это координатные оси Ox и Oy а центр эллипса – это точка O (0;0). Точки пересечения эллипса с его осями называются вершинами эллипса. Таким образом, эллипс имеет четыре вершины A′, A, B′, B .
Рис. 6
Отрезки A′A и B′B (а также их длины 2a и 2b ) тоже принято называть осями эллипса: A′A − большая ось эллипса; B′B − малая ось эллипса (соответственно, 2a − большая ось эллипса; 2b − малая ось эллипса). В этом случае отрезки OA и OB (а также их длины a и b ) принято называть полуосями эллипса: OA − большая полуось эллипса; OB − малая полуось эллипса (соответственно, a − большая полуось эллипса; b − малая полуось эллипса).
Пусть M (x, y) − произвольная точка эллипса. Отрезки F1M и F2 M (а также их длины r1 и r2 ) называются фокальны-
ми радиусами точки М.
Из определения эллипса следует, что r1 + r2 = 2a .
Подчеркнем еще раз, что величина b (малая полуось эллипса), входящая в каноническое уравнение эллипса, однозначно определяется величинами a и c по формуле b = a2 −c2 .
Если окажется, что b = a , то каноническое уравнение эллипса принимает вид |
|
x2 + y2 = a2 , |
(39) |
а уравнение (39) определяет окружность с центром в точке O (0;0) радиуса a . Следовательно, окружность можно рассмат-
ривать как частный случай эллипса.
Во многих задачах линия второго порядка задается общим уравнением, т.е. уравнением вида (35). Чтобы построить такую линию, нужно вначале уравнение (35) привести к каноническому виду, исходя из которого можно построить искомую линию.
Если в уравнении (35) B = 0 , т.е. отсутствует член с произведением текущих координат, то для приведения такого уравнения к каноническому виду достаточно применить формулы сокращенного умножения a2 −2ab +b2 = (a −b)2 или a2 + 2ab +b2 = (a +b)2 .
Может случиться, что при приведении общего уравнения линии второго порядка к каноническому виду получится уравнение вида (37):
|
x2 |
+ |
y2 |
=1 , |
(40) |
|
a2 |
b2 |
|||
|
|
|
|
||
но a < b . В этом случае уравнение (40) определяет эллипс следующего вида показанного на рис. 7 (переменные x и |
y по- |
||||
менялись ролями); a = b2 −c2 , т.е. c = b2 −a2 . |
|
|
|
|
|
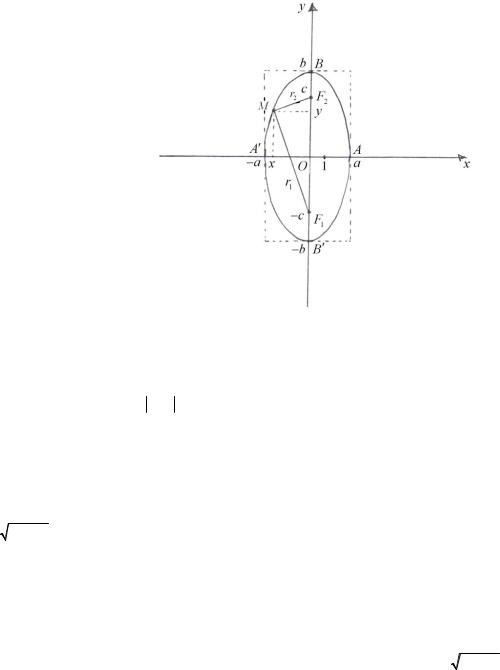
Рис. 7
Гипербола :: = геометрическое место точек плоскости, для каждой из которых модуль разности расстояний до двух фиксированных точек F1 , F2 этой плоскости есть постоянная величина 2a и эта постоянная меньше расстояния между точками F1 и F2 : 2a < 2c , где 2c = F1F2 , при этом точки F1 и F2 называются фокусами гиперболы.
Рассмотрим на плоскости гиперболу с фокусами F1 , F2 . Введем на этой плоскости ДПСК следующим образом: в качестве оси абсцисс возьмем прямую (F1F2 ) , считая ее направленной от F1 к F2 ; начало координат поместим в середине отрезка F1F2 . При таком выборе ДПСК уравнение данной гиперболы имеет вид
|
x2 |
− |
y2 |
=1, |
(41) |
|
a2 |
b2 |
|||
|
|
|
|
||
где b = c2 −a2 (величина b является вещественным числом, ибо по определению гиперболы 2a < 2c , т.е. |
a < c ). |
||||
Уравнение (41) называется каноническим уравнением гиперболы. Уравнение (41) является алгебраическим уравнением второй степени, следовательно, гипербола – это линия второго порядка.
В уравнение (41) текущие координаты x , y переменой точки M (x, y), принадлежащей гиперболе, входят в четной степени, следовательно, гипербола симметрична относительно координатных осей Ox и Oy . Поэтому для построения ги-
перболы достаточно исследовать форму части гиперболы, расположенной в первой координатной четверти, т.е. построить график функции
y = |
b |
x2 −a2 , |
(42) |
|
a |
||||
|
|
|
при x ≥ a (выражение (42) получено из формулы (41)), а затем с помощью зеркальных отражений полученного графика относительно координатных осей восстановить форму гиперболы в остальных координатных четвертях. В результате указанных операций получается, что гипербола имеет форму, представленную на рис. 8.
Координатные оси Ox и Oy являются осями симметрии гиперболы (оси симметрии гиперболы называют обычно осями гиперболы), а начало координат – центром симметрии гиперболы (центр симметрии гиперболы называют обычно центром гиперболы). Таким образом, оси гиперболы – это координатные оси Ox и Oy , а центр гиперболы – это точка O (0;0).
Точки пересечения гиперболы с ее осью называются вершинами гиперболы. Таким образом, гипербола имеет две вершины
A′ и A .
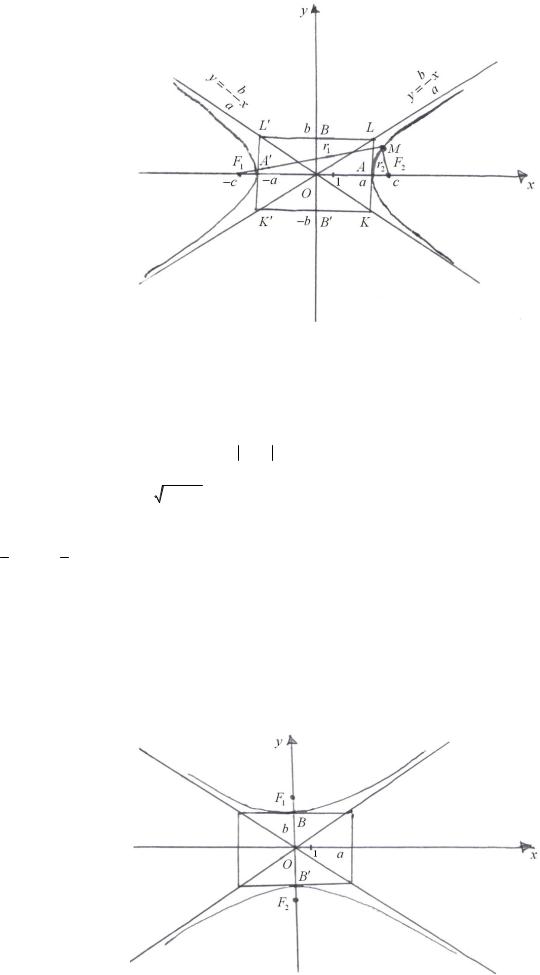
|
Рис. 8 |
′ |
′ |
Отрезки A A и |
B B (а также их длины 2a и 2b ) тоже принято называть осями гиперболы. В этом случае отрезки OA |
и OB (а также их длины a и b ) принято называть полуосями гиперболы. |
|
Пусть M (x, y) |
− произвольная точка гиперболы. Отрезки F1M и F2 M (а также их длины r1 и r2 ) называются фокаль- |
ными радиусами точки M .
Из определения гиперболы следует, что r1 −r2 = 2a .
Подчеркнем еще раз, что величина b , входящая в каноническое уравнение гиперболы, однозначно определяется вели-
чинами a и c по формуле b = c2 −a2 .
Прямоугольник LKK ′L′ со сторонами 2a и 2b , расположенный симметрично осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы. Диагонали основного прямоугольника гиперболы, т.е. прямые
y = ba x , y = − ba x являются асимптотами гиперболы.
При построении гиперболы удобно вначале изобразить ее основной прямоугольник и провести асимптоты, а затем изобразить саму гиперболу.
Может случиться, что при приведении общего уравнения линии второго порядка к каноническому виду получится уравнение вида
− |
x2 |
+ |
y2 |
=1. |
(43) |
|
a2 |
b2 |
|||||
|
|
|
|
|||
В этом случае уравнение (43) определяет гиперболу вида, показанного на рис. 9 (переменные x и y |
поменялись ролями). |
|||||
Рис. 9
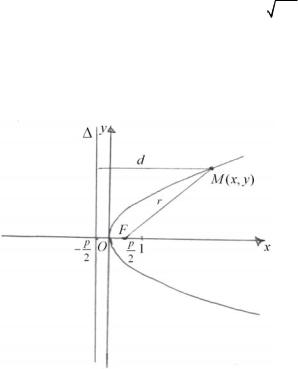
Парабола :: = геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки F
этой плоскости равно расстоянию до фиксированной прямой ∆ данной плоскости, при этом, точка F называется фокусом параболы, прямая ∆ – директрисой параболы.
Расстояние p от фокуса F до директрисы ∆ , т.е. длина перпендикуляра, проведенного из точки F к прямой ∆ , назы-
вается параметром параболы.
Рассмотрим на плоскости параболу с фокусом F , директрисой ∆ и параметром p . Введем на этой плоскости ДПСК
следующим образом: в качестве оси абсцисс возьмем прямую, проходящую через фокус F и перпендикулярную к директрисе ∆ , считая ее направленной от директрисы к фокусу; начало координат поместим в середине перпендикуляра, проведенного из фокуса к директрисе. При таком выборе ДПСК уравнение данной параболы имеет вид
y2 = 2 px . |
(44) |
Уравнение (44) называется каноническим уравнением параболы, оно является алгебраическим уравнением второй степени, следовательно, парабола – это линия второго порядка.
В уравнение (44) текущая координата y переменой точки M (x, y), принадлежащей параболе, входит в четной степени,
следовательно, парабола симметрична относительно координатной оси Ox . Поэтому для построения параболы достаточно исследовать форму части параболы, расположенной в первой координатной четверти, т.е. построить график функции
y = 2 px , |
(45) |
при x ≥ 0 (выражение (45) получено из формулы (44)), а затем с помощью зеркального отражения полученного графика относительно оси Ox восстановить форму гиперболы в четвертой координатной четверти. В результате указанных операций получается, что парабола имеет форму, показанную на рис. 10.
Рис. 10
Координатная ось Ox является осью симметрии параболы (ось симметрии параболы называют обычно осью параболы). Точка пересечения параболы с ее осью называется вершиной параболы. Таким образом, точка O (0;0) является вершиной параболы.
Пусть M (x, y) – произвольная точка параболы. Отрезок FM (а также его длина r ) называется фокальным радиусом
точки M .
Из определения параболы следует, что r = d , где d − расстояние от точки M до директрисы ∆ .
Может случиться, что при приведении общего уравнения линии второго порядка к каноническому виду получится
уравнение вида |
|
y2 = −2 px , p > 0 . |
(46) |
В этом случае уравнение (46) определяет параболу вида, показанного на рис. 11.
