
k_Fomin
.pdf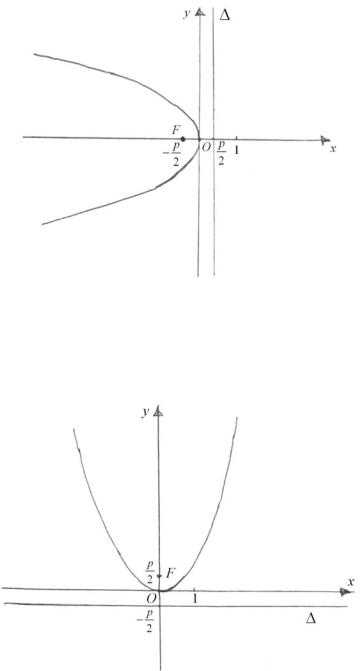
Рис. 11
Если после преобразований получится уравнение вида
x2 = 2 py ,
то это уравнение определяет параболу вида, показанного на рис. 12.
Рис. 12
Уравнение
x2 = −2 py
определяет параболу вида, представленного на рис. 13.

Рис. 13
Задача 2.2. Привести уравнение кривой второго порядка f (x, y) = 0 к каноническому виду и найти точки пересечения ее с прямой Ax + By +C = 0 . Построить графики кривой и прямой.
4x2 −9 y2 −8x −36y −68 = 0 , x +3 = 0 .
Решение.
Используя формулы алгебры
a2 + 2ab +b2 = (a +b)2 ; a2 −2ab +b2 = (a −b)2 ,
преобразуем левую часть уравнения кривой, выделяя полные квадраты двучленов: |
|
|
|
|
|
|
|
||||||||||||||||||||
4(x2 −2x +1) |
−4 −9(y2 + 4y + 4)+36 −68 = 0 ; |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
4(x −1)2 −9(y + 2)2 = 36 . |
|
|
|
|
|
|
|
|
||||||||||||||||
Разделим обе части полученного уравнения на 36: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x −1)2 |
(y + |
2)2 |
(47) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
− |
|
|
4 |
=1 . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Введем новые координаты X , Y по формулам X = x −1 , |
Y = y + 2 . Тогда X = 0 , Y = 0 при x =1 , |
y = −2 , т.е. новое начало |
|||||||||||||||||||||||||
координат имеет вид O1 (1; −2), а уравнение (47) принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X 2 |
− |
Y 2 |
=1 . |
(48) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
Уравнение (48) является каноническим уравнением гиперболы в ДПСК XO1Y с полуосями a = 3 , b = 2 . |
|||||||||||||||||||||||||||
Найдем точки пересечения гиперболы с прямой x +3 = 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
−9 y |
2 |
−8x |
−36 y −68 = 0 ; |
|
|
|
|
|
|
|
|
||||||||||
|
|
4x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
+3 |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из второго уравнения системы получаем x = −3 . Тогда первое уравнение системы принимает вид |
|
||||||||||||||||||||||||||
|
|
4(−3)2 −9 y2 −8(−3) −36y −68 = 0 |
|
|
|
|
|
|
|
|
|||||||||||||||||
или после упрощения |
|
|
|
|
|
|
|
9 y2 +36 y +8 = 0 . |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решая полученное квадратное уравнение, находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
y = |
−6 −2 7 |
; |
y |
2 |
|
= |
−6 + 2 7 |
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, прямая x +3 = 0 пересекает гиперболу в двух точках |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
M |
|
|
|
−6 −2 7 |
M |
|
|
|
−6 + 2 7 |
|
|
|
|
|
|
|
|
||||||||||
1 |
−3; |
|
|
|
|
|
|
|
|
; |
2 |
|
−3; |
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выполним чертеж (рис. 14).
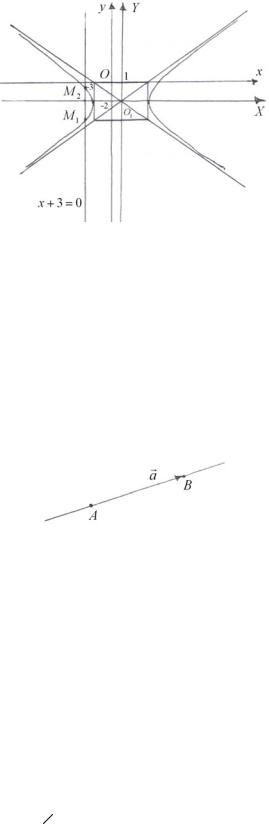
Рис. 14
Задача 2.2 решена.
2.3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ В ПРОСТРАНСТВЕ
Рассмотрим произвольную прямую в пространстве. Возьмем на данной прямой две произвольные точки, обозначим их
через А и В. uuur
Вектор АВ :: = направленный отрезок, т.е. отрезок прямой, ограниченный точками А и В, при условии, что точка А
считается началом отрезка, точка В – концом отрезка (точки А и В называются соответственно началом и концом вектора uuur
AB ; начало вектора т.е. точку А, называют также точкой приложения вектора).
Вектор можно обозначать так же одной малой буквой латинского алфавита (на чертеже эта буква ставится около конца uur
стрелки, обозначающей вектор). Например, вектор AB можно обозначить через а (рис. 15).
Рис. 15
Заметим, что любые две точки произвольной прямой определяют два вектора. Например, точки А и В определяют такие
вектора: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
uuur |
− вектор с началом в точке А и концом в точке В; |
|
|
|
||||||||||||||||
|
AB |
|
|
|
|||||||||||||||||
|
uuur |
− вектор с началом в точке В и концом в точке А. |
|
|
|
||||||||||||||||
|
ВА |
|
|
uur |
|||||||||||||||||
|
Нулевой вектор |
|
|
|
|
|
|
|
|
||||||||||||
|
:: = вектор, начало и конец которого совпадают (обозначение: 0 , АА или 0). |
||||||||||||||||||||
|
Нулевой вектор изображается на чертеже точкой. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uuur |
|
|
|
|
|
||
|
Длина (или модуль) вектора AB :: = расстояние между началом и концом этого вектора, измеренное с помощью задан- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uuuur |
r |
|
|
|
|
||
ной единицы измерения (обозначение: |
АВ |
, |
a |
). |
|
|
|
||||||||||||||
|
Заметим, что |
uur |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
0 |
|
=0. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Векторы |
|
r |
и |
|
|
r |
называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. |
|||||||||||||
|
|
а |
r |
b |
|||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(обозначение: a ||b ). |
|
|
|
|
r |
|
|
|
|||||||||||||
|
Обозначение неколлинеарных векторов: |
r |
|
|
|
||||||||||||||||
|
a || b . |
|
|
|
|||||||||||||||||
|
Нулевой вектор принято считать коллинеарным любому вектору, так как он не имеет определенного направления. |
||||||||||||||||||||
|
Векторы |
|
r |
и |
|
|
r |
называются сонаправленными, если они коллинеарны и имеют одинаковое направление (обозначение: |
|||||||||||||
r |
а |
|
b |
||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а ↑↑ b ). |
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
||||
|
Векторы |
|
и |
|
|
называются противоположно направленными, если они коллинеарны и имеют противоположное на- |
|||||||||||||||
|
|
а |
|
|
b |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
|
|
||
правление (обозначение: а ↑↓ b ). |
|
|
|
|
|
||||||||||||||||
|
Векторы |
r |
и |
|
r |
называются равными, если |
|
|
|
|
|||||||||||
|
а |
b |
|
|
|
|
|||||||||||||||
|
1) |
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
↑↑ b ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2) |
r |
= |
|
r |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uur uuur |
uur uuur |
uur |
uuuur |
Например, для векторов, изображенных на рис. 16, AB = CD , |
PQ ≠ PR , |
EF |
≠ GH . |
||||||||||||||||||
Рис. 16
uur
Пусть дан некоторый вектор а и некоторая точка P . Тогда можно построить вектор PQ с началом в точке P , равный вектору аr (рис. 17).
Рис. 17
Таким образом, каковы бы ни были вектор |
r |
и точка |
P , существует, и притом только один, вектор |
uur |
с началом в |
а |
PQ |
точке P , равный вектору аr . Иначе говоря, для каждого вектора точка его приложения может быть выбрана где угодно. Со-
ответственно этому в векторной алгебре векторы рассматриваются с точностью до их положения, т.е. не различаются равные |
||||
векторы, получающиеся друг из друга параллельным переносом. В этом смысле векторы называются свободными. |
||||
r r |
r |
r |
r |
r |
Сумма a +b |
векторов а |
и b |
:: = вектор c , идущий из начала вектора а в конец вектора |
b , при условии, что вектор b |
приложен к концу вектора аr |
(сложение векторов по правилу треугольника), рис. 18. |
|
||
|
|
|
Рис. 18 |
|
|
|
|
|
r r |
|
r |
|
r |
тор |
rСумма |
a +b |
представляет собой диагональ параллелограмма, построенного на векторах |
а |
и |
b , при условии, что век- |
b приложен к началу вектора а (сложение векторов по правилу параллелограмма). |
|
|
|
|||
|
|
|
|
|
|
r |
Рис. 19 |
r |
|
|
|
|
|
|
|
и b по указанному правилу конец вектора |
совпадет с началом вектора |
||
r |
Если окажется, что при сложении векторов а |
b |
|||||||
|
r |
r |
r |
|
|
|
|
|
|
а, то |
a +b = 0 . |
|
|
|
|
||||
|
Противоположный вектор −a для вектора аr |
:: = вектор, начало которого совпадает с концом вектора а, а конец – с |
|||||||
началом вектора аr |
(рис. 19). |
|
|
|
|||||
|
Операция сложения векторов обладает следующими свойствами: |
|
|
||||||
|
1) |
r |
r |
r |
r |
|
|
|
|
|
a +b = b + a (свойство коммутативности); |
|
|
|
|||||
|
|
|
r |
r |
r |
r r r |
|
|
|
|
2) |
a +(b |
+c)= (a +b)+ c (свойство ассоциативности); |
|
|
||||
|
3) |
r |
r |
r |
|
|
|
|
|
|
a +0 = a ; |
r |
|
|
|
||||
|
|
|
r |
|
r |
|
|
|
|
|
4) |
a +(−a)= |
0 |
|
|
|
|||
(здесь |
r |
r |
r |
− произвольные векторы). |
|
|
|
||
а, b |
, c |
|
|
|
|||||
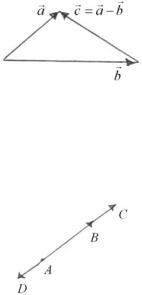
|
Заметим, что в силу свойства ассоциативности мы имеем право говорить о сумме трех векторов |
r r r |
и записывать ее в |
||||
|
а, b , c |
||||||
|
r r r |
r |
r r r r r |
r |
r r r r r |
|
|
виде |
a +b +c , неуказывая приэтом, считаем лимы |
a +b +c = a +(b +c) или |
a +b +c = (a +b)+c . |
|
|
||
r r |
r |
и b |
:: = вектор |
r |
Рис. 20 |
r |
|
Разность a −b векторов а |
c , который в сумме с вектором b дает вектор а (рис. 20). |
||||||
|
|
|
r |
r |
|
r |
есть вектор, идущий из конца вычи- |
Из рисунка видно, что если векторы а |
и b |
имеют общее начало, то разность a −b |
|||||
таемого вектора в конец уменьшаемого вектора. |
|
|
|
||||
r |
вектора |
r r |
на число λ ≠ 0 |
:: = вектор c , определяемый следующими условиями (рис. 21): |
|||
Произведение λa |
a ≠ 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 21 |
|
|
1) |
|
c | | a ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
r |
r |
|
|
|
||
|
c ↑↑ a |
|
при λ > 0 , c ↑↓ a при λ < 0 ; |
|
|
|
||||||||||||||||
3) |
|
cr |
|
= |
|
λ |
|
|
|
ar |
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
uuur |
|
|
|
3 uuur |
|
|
uuur |
|
1 uuur |
|
|
|
|
|||||||||
AC |
= |
|
|
AB ; AD = − |
|
AB . |
|
|
|
|||||||||||||
2 |
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
r r |
|
|
|
|||
Если λ = 0 или а |
= 0 |
, то, по определению, λa = 0 . |
|
|
|
|||||||||||||||||
Операция умножения вектора на число обладает следующими свойствами: |
|
|
||||||||||||||||||||
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|||||
1) |
1 a =r a ; |
|
|
r |
|
|
|
|
|
|
|
|||||||||||
2) |
|
λ(µa)= (λµ)a ; |
|
|
|
|
|
|
||||||||||||||
3) |
|
|
|
|
|
|
|
|
|
r |
|
|
r |
r |
|
|
|
|
|
|
||
|
(λ+µ)a |
= λa +µa ; |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
r |
|
|
r |
|
|
r |
r |
|
|
|
|
|
|
||||
4) |
|
λ(a |
+b) |
= λa +λb |
|
|
r r |
|
|
|
||||||||||||
(здесь λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
, µ − произвольные числа; а, b − произвольные векторы). |
|
|
||||||||||||||||||||
Заметим, |
что вектор |
|
r |
противоположный вектору |
r |
r |
в виде |
|||||||||||||||
−a , |
а, можно записать в виде −a = (−1) a , а разность |
a −b |
||||||||||||||||||||
r r |
r |
+(−1) |
|
r |
|
|
|
|
|
|
|
|
|
|
||||||||
a −b = a |
b . |
|
|
|
|
|
|
|
||||||||||||||
Операции сложения векторов и умножения вектора на число называются линейными операциями над векторами. Пусть в пространстве задана ДПСК, аr − некоторый вектор. Вектор а можно приложить к началу координат, т.е. к точ-
ке O (0;0;0).
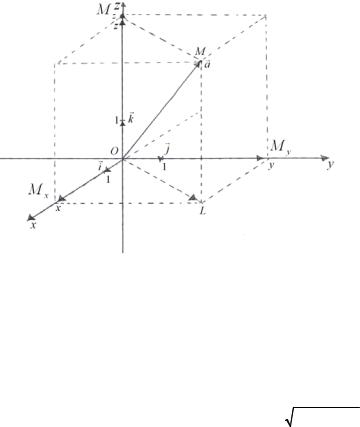
Декартовы прямоугольные координаты x , y , z вектора а :: = проекции вектора а на координатные оси Ox , Oy , Oz
(рис. 22), где M x , M y , M z − проекции точки М на координатные оси Ox , Oy , Oz .
|
|
|
Рис. 22 |
|
|
|
|
|
|
|
|
|
|
Тот факт, что вектор аr имеет координаты x , y , z , отмечают следующим образом: |
|
||||||||||||
|
|
|
a ={x, y, z}. |
|
|
|
|
|
|
|
|
|
|
Таким образом, в рассматриваемой ДПСК координаты вектора а − это координаты конца M этого вектора при условии, что |
|||||||||||||
аr приложен к началу координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Из чертежа (рис. 22) видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим единичные векторы координатных осей: |
|
|
ar |
|
|
= x2 + y2 + z2 . |
(49) |
||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
ri ={1; 0; 0}; |
j ={0;1; 0}; k ={0; 0;1}. |
|
|
|||||||||
Из чертежа (рис. 22) видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uuuuur |
r |
uuuur |
r |
uuuur |
r |
|
|
|
|
|
|
|
|
OM x |
= xi , |
OM y |
= y j , |
OM z |
= zk |
; |
|
|
|
|
||
|
uuur |
uuuuur |
uuuuur |
|
uuur uuuuur |
|
|
|
|
|
|
||
|
OL = OM x |
+OM y |
; a = OL +OM z |
, |
|
|
|
|
|
||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r r |
(50) |
|
|
|
|
|
|
|
|
|
|
a = xi |
+ y j + zk . |
||
Таким образом, любой вектор аr |
можно представить с помощью векторов i , j , k |
в виде (50). |
|
||||||||||
По этой причине векторы ri |
, j , kr называются базисными векторами, а упорядоченная тройка векторов ( i , j , k ) – ор- |
||||||||||||
тонормированным базисом, ибо это векторы взаимно ортогональны и длина каждого из них равна единице. Соотношение |
||||
(50) называется разложением вектора аr |
по базису ( i , j , k ). |
|
|
|
r |
Укажем, как проводятся линейные операции над векторами в случае, когда векторы заданы своими координатами: если |
|||
r |
|
|
|
|
a = |
{x1, y1, z1}, b ={x2 , y2 , z2}, то |
|
|
|
|
|
r |
y1 + y2 , z1 + z2}, |
|
|
|
a +b ={x1 + x2 , |
(51) |
|
т.е. при сложении векторов, их соответствующие координаты складываются; |
|
|
||
|
|
r |
− x2 , y1 − y2 , z1 − z2}, |
|
|
|
a −b ={x1 |
(52) |
|
т.е. при вычитании векторов, их соответствующие координаты вычитаются.
r
Если a ={x, y, z}, λ − некоторое число, то
|
|
λa ={λx, λy, λz}, |
|
(53) |
т.е. при умножении вектора на число каждая координата этого вектора умножается на данное число. |
|
|||
|
uuur |
известны координаты его начала и конца: A(x1, y1, z1 ), B (x2 , y2 , z2 ), то |
|
|
Если для вектора |
AB |
|
|
|
|
|
uur |
− z1}, |
|
|
|
AB ={x2 − x1, y2 − y1, z2 |
(54) |
|
т.е. для нахождения координат вектора |
uuur |
нужно из координат его конца вычесть соответствующие координаты его начала. |
|||||||
AB |
|||||||||
|
|
|
uur |
uuur |
uuur |
uur |
={x2 , y2 , z2}, |
uuur |
, y1, z1}, а также |
Действительно, из чертежа (рис. 23) видно, что |
AB |
= OB |
−OA . Учитывая, что |
OB |
OA ={x1 |
||||
формулу (52), приходим к (54).
Рис. 23
В силу (49), (54)
|
|
|
|
|
|
|
|
|
|
|
|
uuur |
= (x − x )2 +(y |
|
|
− y |
)2 +(z |
|
− z |
)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
AB |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
uuur |
|
|
|
|
|
|
|
− длина отрезка AB , следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Но |
AB |
|
= |
AB |
, где |
AB |
|
|
|
|
|
AB |
|
= |
|
(x |
− x |
)2 +(y |
2 |
− y |
)2 |
+(z |
2 |
− z |
)2 . |
(55) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
||
|
Формула (55) позволяет вычислять расстояние между двумя точками пространства. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
rr |
|
|
r |
r |
число, |
равное произведению модулей этих векторов на косинус угла |
||||||||||||||||||||||||
|
Скалярное произведение ab векторов a |
и b :: = |
|||||||||||||||||||||||||||||||||||||
между ними: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rr |
|
r |
|
r |
cos ϕ, |
|
|
|
|
|
(56) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab = |
a |
b |
|
|
|
|
|
|||||||
где |
|
r r |
|
|
|
|
r |
|
r |
(по определению, 0 ≤ ϕ ≤ π). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ϕ = a , b |
− угол между векторами |
a |
|
и b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Скалярное произведение обладает следующими свойствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
rr |
rr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1) |
|
abr= rba ; |
rr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2) |
|
(λa)b = λ(ab); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
r r |
|
r |
rr rr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3) |
|
a (b +c)= ab + ac |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
r |
|
r |
r |
|
|
|
|
λ − произвольное число). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(здесь a , b , |
c − произвольные векторы, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
:: = скалярное произведение вектора a |
на самого себя: |
|
|
|
|
|
|
||||||||||||||||||||||
|
Скалярный квадрат ar2 вектора a |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ar2 = aa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Заметим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
= |
|
r |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из формулы (56) следует, что
rr cos ϕ = rabr ,
a b
тогда
rr
ϕ = arccos rabr a b
r r
(последние две формулы имеют место при условии, что a ≠ 0 и b ≠ 0 ). Признак ортогональности (перпендикулярности) векторов:
r rr
a b ab = 0 .
|
r |
, y1, z1}, |
r |
, y2 , z2}, то |
Если |
a ={x1 |
b ={x2 |
r
ab = x1x2 + y1 y2 + z1z2 ,
т.е. скалярное произведение векторов равно сумме произведений соответствующих координат этих векторов. Первый признак коллинеарности векторов: пусть a ={x1, y1, z1}, b ={x2 , y2 , z2}, тогда
|
r r |
|
x1 |
|
y1 |
|
z1 |
|
|||
|| |
a b |
|
= |
= |
, |
||||||
|
|
||||||||||
|
|
|
x |
|
y |
2 |
|
z |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|||
т.е. векторы коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны.
r r r
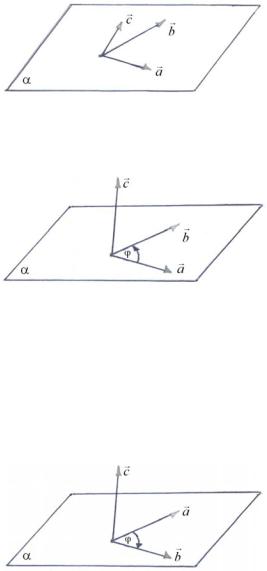
Векторы a , b , c называются компланарными, если они расположены на одной плоскости или параллельных плоскостях (рис. 24).
Рис. 24
rr
Впротивном случае векторы a , b , c называются некомплонарными (рис. 25).
|
|
|
Рис. 25 |
|
|
|
r r |
Упорядоченная тройкаr |
( a , b , c ) некомпланарных векторов называется правоориентированной или просто правой, если |
||
из конца третьего вектора c |
кратчайший поворот от первого вектора ко второму виден против часовой стрелки при условии, |
||
r |
r |
r |
r r r |
что векторы a , |
b , |
c приложены к одной общей точке. В противном случае тройка векторов ( a , b , c ) называется левоори- |
|
ентированной или левой.
На последнем чертеже (рис. 25) тройка векторов ( a , b , c ) является правой. r r r
На чертеже (рис. 26) тройка векторов ( a , b , c ) является левой.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 26 |
Векторное произведение |
r r |
|
|
r |
r |
r |
||||||||||
a ×b |
векторов a ≠ |
0 |
и b ≠ 0 :: = вектор c , определяемый следующими условиями: |
|||||||||||||
1) |
вектор cr |
перпендикулярен плоскости векторов a и b при условии, что a и b приложены к одной общей точке; |
||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
r |
r |
r |
|
|
упорядоченная тройка векторов ( a , b |
, c ) является правой; |
|||||||||||||||
3) |
|
r |
|
= |
r |
|
|
r |
|
|
r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
c |
|
a |
b |
|
sin ϕ, где ϕ = a , b |
|
|
|
|
||||||
r |
|
r |
, или |
r r |
|
|
r |
r |
|
r |
||||||
|
|
|
|
|||||||||||||
(если a = 0 |
b = 0 , то, по определению, |
a ×b = 0 ) (рис. 27). |
||||||||||||||

|
|
|
|
r r |
|
Рис. 27 |
|
|
||
Модуль векторного произведения |
равен площади параллелограмма, построенного на векторах a |
и b |
при усло- |
|||||||
a ×b |
||||||||||
вии, что |
r |
r |
приложены к одной общей точке: |
|
|
|||||
a |
и b |
|
|
|||||||
|
|
|
|
|
|
r r |
= Sпар . |
|
|
|
|
|
|
|
|
|
a ×b |
|
|
||
Площадь треугольника, построенного на векторах a и b при условии, что a и b приложены к одной общей точке, выражается формулой
Sтр = 12 ar×br .
Второй признак коллинеарности векторов:
ar||b ar×b = 0 .
Векторное произведение обладает следующими свойствами: |
||||||||
|
r |
|
r |
r |
r |
|
|
|
1) |
a |
×rb =r−b×ar; |
r |
|
||||
2) |
(λa)×b = λ(a ×b); |
|
||||||
|
r |
|
r |
r |
r |
r |
r |
r |
3) |
a |
×(b +c)= a ×b + a ×c |
||||||
(здесь |
r r |
r |
− произвольные векторы; λ − произвольное число). |
|||||
a , b |
, c |
|||||||
|
|
r |
|
|
|
r |
={x2 , y2 , z2}, то |
|
Если |
a ={x1, y1, z1} |
, b |
||||||
r r a ×b =
r |
r |
r |
|
|
i |
j |
k |
|
|
x1 |
y1 |
z1 |
. |
(57) |
x2 |
y2 |
z2 |
|
|
Символический определитель в правой части (57) раскрывается по элементам первой строки:
|
|
|
r |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
k |
r |
|
|
y |
z |
|
r |
|
x |
z |
|
r |
|
|
x |
y |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x |
y |
z |
= i |
|
1 |
1 |
|
− j |
|
1 |
1 |
|
+ k |
|
1 |
1 |
|
|
|
|
|||
|
|
|
1 |
1 |
1 |
|
|
|
y2 |
z2 |
|
|
x2 |
z2 |
|
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
x2 |
y2 |
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Смешанное произведение |
rrr |
векторов |
r r |
|
:: = |
скалярное произведение вектора |
r r |
на вектор |
r |
|||||||||||||||||
abc |
a , b , c |
a ×b |
c : |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
rrr |
|
r r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
abc = |
(a ×b)c . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Абсолютная величина (модуль) смешанного произведения векторов a , b , c равна объему параллелепипеда, построенно- r r r r rrr
го на векторах a , b , c при условии, что векторы a , b , c приложены к одной общей точке (рис. 28): abc =Vпар .
Рис. 28
|
|
|
r |
, c при условии, что векторы a , b , c приложены к одной общей точке, |
||||||||||||||
Объем пирамиды, построенной на векторах a , b |
||||||||||||||||||
выражается формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
rrr |
|
|
|
|
|
|
||
|
|
|
|
V |
|
|
= |
|
|
|
abc |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
пир |
|
6 |
|
|
|
|
|
|
|
|
|
|||
Признак компланарности векторов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
rr |
|
|
|
|
|
a |
, b , c |
компланарны abc = 0 . |
|
|
|
|||||||||||
r |
r |
r |
, y3 , z3}, то |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если a ={x1, y1, z1}, b ={x2 , y2 , z2}, c ={x3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
rrr |
|
|
x1 |
|
|
|
y1 |
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
abc |
= |
x2 |
|
|
y2 |
|
z2 |
|
. |
|
|
|
|||
|
|
|
|
|
|
|
x3 |
|
|
|
y3 |
|
z3 |
|
|
|
|
|
|
|
rr |
|
|
|
|
|
ruur |
|
|
|
|
r r |
|
r r |
|||
Скалярное произведение ab обозначается также через (a,b), |
векторное произведение |
a ×b |
− через |
a,b , смешанное |
||||||||||||||
rrr |
|
r r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
произведение abc |
− через |
(a,b, c). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rr
Задача 2.3. Даны векторы a , b и c . Для векторов, указанных в пп. а) – д), выполнить соответственно следующие операции:
а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение векторов;
г) проверить векторы на коллинеарность и ортогональность; д) проверить, будут ли компланарны векторы.
|
|
|
|
|
|
|
r |
= |
r |
r r |
; |
r |
r r |
; |
r |
r r |
|
|
|
|
|
|
|
a |
2i |
−3 j + k |
b = i |
− 2 j +7k |
c = i |
−3 j + 2k . |
|||
|
r |
r |
r |
r |
|
|
r |
r |
|
r |
|
|
|
|
|
|
а) |
r−2ar, |
b , |
−2rc ; бr) |
−6ra |
, |
4c ; в) 3b , |
−8c ; |
|
|
|
|
|
|
|||
г) |
b , c ; д) 5a , 4b , 3c . |
|
|
r r |
|
|
|
|
|
|
|
|
|
|||
Решение. Запишем векторы |
в координатной форме: |
|
|
|
||||||||||||
a , b , c |
|
|
|
|||||||||||||
a={2; −3;1},
b={1; −2; 7},
c={1; −3; 2}.
а) |
|
r r |
|
|
r |
|
|
rrr |
|
|
|
2 |
|
|
|
−3 |
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
= |
|
= 4 |
|
1 |
|
|
|
−2 |
7 |
|
= |
|
|
|
|
|||||||||||||||
(−2a)b(−2c) |
4abc |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
−3 |
2 |
|
|
|
|
|
|
|
|||||
|
= 4 [2 (−2) 2 +(−3) 7 1+1 (−3) 1−1 (−2) 1−(−3) 1 2 − |
||||||||||||||||||||||||||||||||
|
– 7 (−3) 2] = 4 (−8 −21−3 + 2 + 6 + 42) = 4 (50 −32) = 4 18 = 72 ; |
||||||||||||||||||||||||||||||||
|
|
r |
r |
|
|
r |
= 72 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(−2a)b(−2c) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
r |
r |
|
||||||
|
|
r |
|
r |
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
i |
|
|
j |
k |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) |
(−6a) |
×(4c)= −24a ×c |
= −24 |
2 |
|
|
|
−3 1 |
= |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
−3 |
2 |
|
|
||||
|
|
|
r |
|
|
−3 1 |
|
|
r |
|
2 1 |
|
|
|
|
r |
|
2 −3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
= −24 i |
|
−3 |
2 |
|
|
− j |
1 2 |
|
|
+ k |
|
1 |
|
|
−3 |
|
|
|
= |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
= −24 (−3ri −3rj −3kr) = 72 (ri + rj + kr) = 72 {1;1;1}; |
||||||||||||||||||||||||||||||||
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−6a) ×(4c)= 72 {1;1;1}; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−6a) ×( |
4c) |
= |
72 {1;1;1} |
= |
72 |
|
|
{1;1;1} |
= 72 12 +12 +12 = 72 3 ; |
||||||||||||||||||||||
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−6a) ×( |
4c) |
= 72 3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
в) |
|
r |
r |
|
|
|
|
rr |
= −24(1 1 |
+ (−2) (−3) +7 2) = |
|||||||||||||||||||||||
(3b)(−8c) |
= −24bc |
||||||||||||||||||||||||||||||||
= −24 (1+6 +14) = −24 21 = −504 ;
