8. Описание педагогических приёмов, использованных в ходе непосредственного взаимодействия с аудиторией

Для наглядности в ходе лекционно-практического занятия было произведено несколько графических изображений.

Материал практического занятия излагался последовательно. Для обеспечения доступности материала основные определения и формулы формулировались однозначно. При подготовке практического занятия я избегал сложных длинных предложений.

9. Анализ самоорганизации на занятии

При проведении практического занятия я достаточно просто нашел общий язык со студентами, поэтому не возникло особых затруднений при объяснении методов решения рассмотренных задач.

При подготовке к занятию я повторил теоретический и практический материалы, которые я сам изучал на занятиях, а также решил несколько новых примеров по данной теме для большей уверенности в своих силах.

В случае, когда студентам было непонятно какое-то математическое действие, я производил его более медленно и подробно, давая необходимые рекомендации для получения правильного результата.

Итогом проведенного практического занятия стало умение студентов решать рассмотренные задачи, а также получение мною нового опыта - передача знаний новому поколению специалистов.

10. Выводы о достижении цели учебного занятия

В ходе практического занятия студенты закрепили материал, по которому уже было проведено лекционное занятие. Рассмотрели методы решения определенных задач, научились решать задания из типового расчета.

Материал был изложен доступным языком и был дан своевременно.

ПРИЛОЖЕНИЕ №1

Неголономная система — механическая система, на которую, кроме геометрических, накладываются и кинематические связи, которые нельзя свести к геометрическим (их называют неголономными). Математически неголономные связи выражаются неинтегрируемыми уравнениями. Движение неголономной системы описывается с помощью специальных уравнений движения (уравнения Чаплыгина, Аппеля, Маджи) или уравнений движения, получаемых из вариационных принципов.

Уравнения Эйлера — Лагранжа преимущественно применяются при рассмотрении неголономных систем, однако их значение не ограничивается этими специальными задачами, так как они позволяют в значительной мере упростить форму и процесс составле­ния уравнений движения и в голономных задачах. Отличительной особенностью данных уравнений является тот факт, что вместо обобщённых скоростей вводятся квазискорости, выражающиеся следующим образом: (*),

где - постоянные коэффициенты,- обобщённые скорости.

Будем исходить из общего центрального уравнения (**)

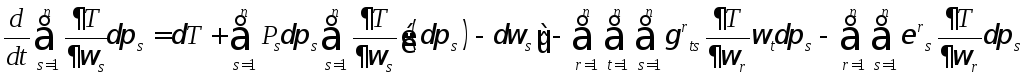
Тре­буется лишь развернуть его левую часть

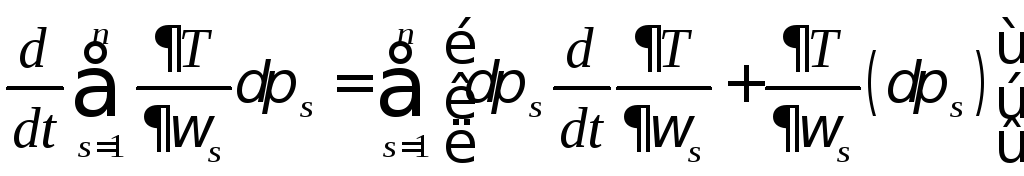(1)

и заменить в правой части его значением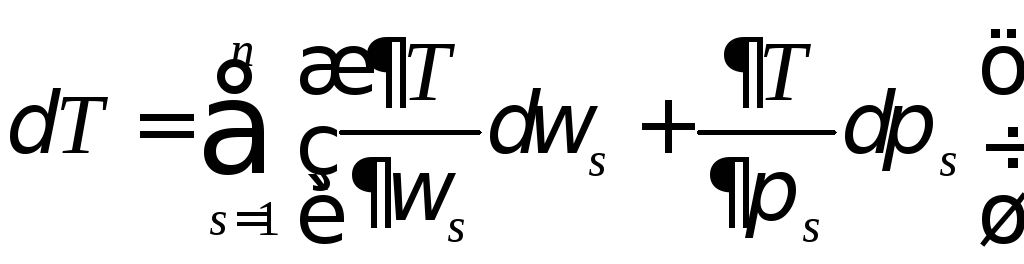(2).

Теперь подстановка в (**) дает

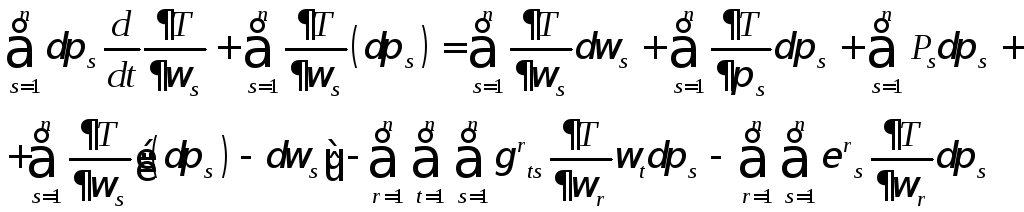(3)

После сокращения приходим к соотношению

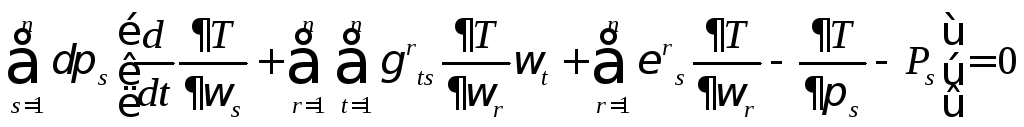(4)

Рассмотрим случаи голономной и неголономной системы по отдельности. В первом случае все вариации независимы и следствием (4) является обращение в нуль коэффициентов при них в этом соотношении. Получаем уравнения движения Эйлера — Лагранжа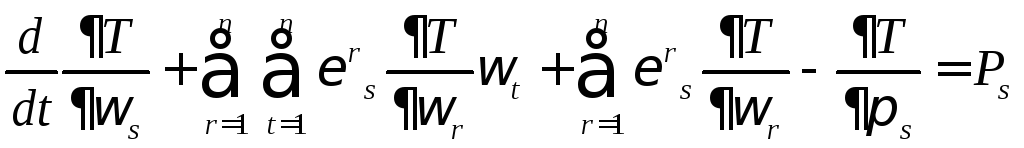, s=1..n (5)

к которым должны быть присоединены кинематические соотношения

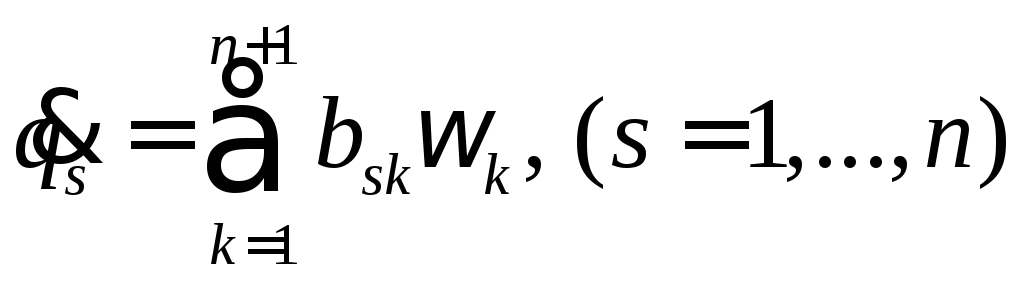(6)

дающие выражения обобщенных скоростей через квазискорости. Получили систему 2n обыкновенных дифференциальных уравнений первого порядка относительно такого же числа неизвестных (7).

Уравнения упрощаются и принимают вид

(7),

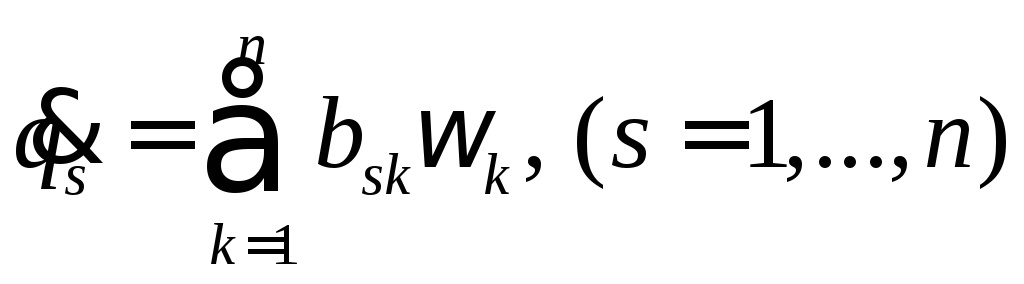(8)

если квазискорости введены с помощью однородных линейных форм с коэффициентами, не содержащими t явно, а не с помощью более общих соотношений.

При наличии неголономных связей в число квазискоростей вносятся линейные формы обобщенных скоростей, обращающиеся в нуль в силу самих уравнений неголономных связей. Последние тогда будут иметь следующий вид:

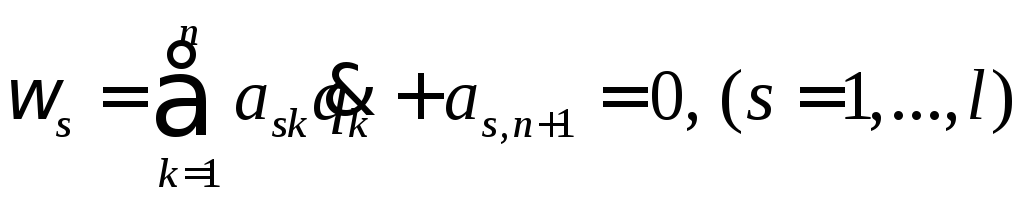(10)

Тогда имеем также

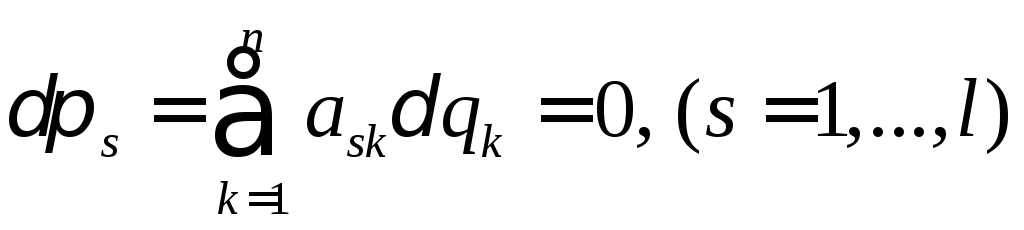(11)

где l - число уравнений неголономных связей. Суммирование по s и t в равенстве (4) поэтому должно производиться от l+1 до n :

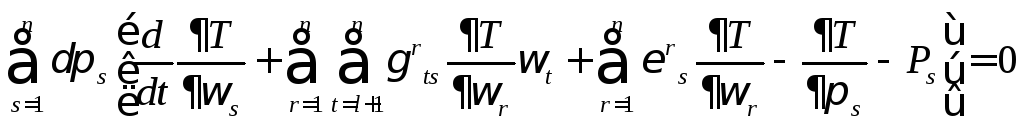(12)

и, поскольку вариации при независимы, величины в квадратных скобках должны быть нулями. Получаемn-l уравнений движения

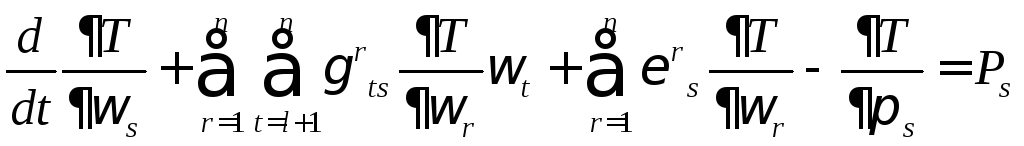, (s = l+1, ... , n) (13)

число которых равно числу степеней свободы. К ним надо присоединить n кинематических соотношений 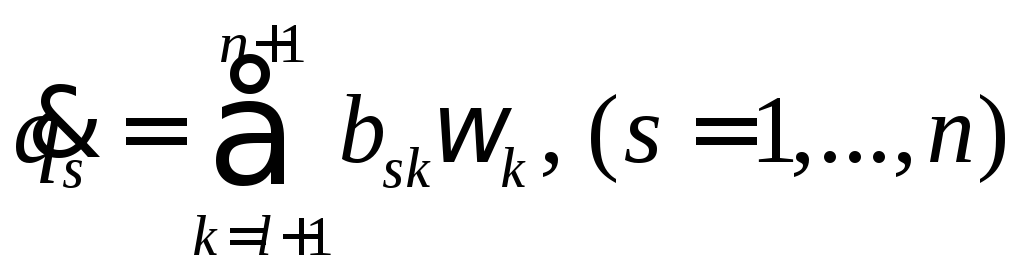(14). Всего имеем уравнений первого порядка, содержащих такое же число неизвестных (15)

Для составления уравнений (13) достаточно знать лишь те символы , в которых нижние индексы соответствуют номерам квазискоростей, не обращающихся в нуль вследствие уравнений неголономных связей. Уравнения (13) содержат производные кинетической энергии Т по всем квазискоростям, в том числе и по тем, которые,

согласно(10) обращаются в нуль. Поэтому при составлении выражения Т неголономные связи нельзя учитывать, они принимаются во внимание лишь после вычисления производных Т по квазискоростям, т. е. квазиимпульсов .

Можно добавить, что в нем достаточно сохранить лишь линейные относительно квазискоростей слагаемые, т. е. не выписывать произведений и квадратов этих

величин, так как после вычисления квазиимпульсов соответствующие слагаемые все равно отпадут в силу уравнений (10). Отметим еще, что в числе линейных относительно величин слагаемых имеются их произведения на. Эти члены, конечно, надо сохранить в выражении Т.

Уравнения движения (5) и (8) обращаются в уравнения Лагранжа, если все квазискорости являются обобщенными скоростями(16)

все символыибудут нулями, а «производные Т по квазикоординатам» станут производными по обобщенным координатам.

Структура выражения кинетической энергии через квазискорости, как правило, гораздо более проста, чем через обобщенные скорости. Этим и объясняется, что уравнения движения в форме Эйлера — Лагранжа оказываются более простыми

по форме и симметричными для значительного класса задач, чем уравнения Лагранжа. Затруднения, связанные с вычислением трехиндексных символов, не столь велики и, во всяком случае, не принципиальны; кроме того, это вычисление при выбранном задании квазискоростей через обобщенные скорости производится один раз навсегда.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Добронравов В.В. Основы механики неголономных систем / В.В. Добронравов. - М.: Высшая школа, 1970 - 264 с.

2. Беленький И.М. Введение в аналитическую механику / И.М. Беленький. - М.: Высшая школа, 1964 - 324 с.

3. Седов Л.И. Механика сплошной среды. Т.2.: Учебник для университетов / Л.И.Седов. – СПб.: Издательство «Лань», 2004. — 560 с.

16