
- •Теория принятия решений
- •Часть 2 нелинейное программирование, теория игр, многокритериальные задачи принятия решений
- •Введение
- •4. Нелинейное программирование
- •4.1. Характеристика задач
- •4.2. Условия оптимальности
- •4.3. Квадратичное программирование
- •4.4. Сепарабельное программирование
- •4.5. Задачи дробно-линейного программирования
- •4.6. Методы спуска
- •4.7. Методы одномерной минимизации
- •4.7.3. Метод деления интервала пополам
- •4.7.4. Метод золотого сечения
- •4.7.6. Метод первого порядка
- •4.8. Многомерный поиск безусловного минимума
- •4.8.1. Метод Гаусса – Зейделя (покоординатного спуска)
- •4.8.2. Метод Хука – Дживса (метод конфигураций)
- •4.8.3. Симплексный метод
- •4.8.4. Градиентные методы
- •4.8.6. Методы сопряженных направлений
- •4.8.7. Методы случайного поиска
- •Алгоритм с возвратом при неудачном шаге
- •Алгоритм с обратным шагом
- •Алгоритм наилучшей пробы
- •Алгоритм статистического градиента
- •4.8.8. Генетические алгоритмы
- •Исходная популяция
- •Результаты работы оператора скрещивания
- •Популяция первого поколения
- •4.9. Методы условной оптимизации
- •4.9.2. Метод проектирования градиента
- •4.9.3. Метод штрафных функций
- •Минимизация по методу Ньютона
- •4.9.4. Метод барьерных функций
- •Результаты поиска алгоритмом барьерных функций
- •4.9.5. Другие методы условной оптимизации
- •5. Методы теории игр в управлении
- •5.1. Теория игр в контексте теории принятия решений
- •5.2. Матричные игры с нулевой суммой
- •Использование линейной оптимизации при решении матричных игр. Пусть игра не имеет оптимального решения в чистых стратегиях, т.Е. Седловая точка отсутствует .
- •5.3. Игры с природой
- •5.4. Критерии, используемые для принятия решений
- •В играх с природой. Критерии, основанные
- •На известных вероятностях стратегий природы
- •Иногда неопределенность ситуации удается в некоторой степени ослабить с помощью нахождения вероятностей состояний на базе данных статистических наблюдений.
- •5.5. Оценка необходимости эксперимента
- •6. Многокритериальные задачи принятия решений
- •6.1. Основы многокритериальный оптимизации
- •6.2. Принцип оптимальности Парето.
- •6.3. Принцип равновесия по Нэшу
- •6.4. Конфликты, переговоры и компромиссы
- •6.5. Краткий обзор методов решения задачи векторной оптимизации
- •Значения компонентов вектор-функции
- •1. Оптимальность по Парето
- •Исходные данные для задачи оптимизации по Парето
- •Эффективность операции
- •2. Принятие решений в условиях неопределенности
- •Исходные данные для задачи принятия решения в условиях неопределенности
- •3. Многокритериальная оптимизация
- •Заключение
- •Библиографический список
- •Оглавление
- •Теория принятия решений
4.9. Методы условной оптимизации
4.9.1. Общие положения
В общем случае задача может содержать ограничения в виде равенств и неравенств, которые и определяют допустимое множество D. Наличие ограничений существенно усложняет решение задачи оптимизации. В большинстве случаев условный оптимум достигается на границе допустимого множества, при этом даже унимодальная функция может иметь на границе несколько локальных экстремумов.
Из большого числа методов условной оптимизации можно выделить 3 основные группы:
методы возможных направлений: метод проектирования градиента, методы Зойтендейка, Вулфа и др.;
методы штрафных и барьерных функций;
модификации методов безусловной оптимизации.
Методы первой группы отличаются способом определения возможных направлений. Направление d в точке xkD называется возможным направлением, если существует 0, при котором
![]()
Эти условия означают, что на направлении d найдутся допустимые точки, в которых значение функции лучше, чем в точке xk.
Ниже рассматривается один из методов возможных направлений.
4.9.2. Метод проектирования градиента
Градиент дает направление, в котором функция возрастает с наибольшей скоростью. Однако при условной оптимизации оно, как правило, не является возможным направлением. Поэтому используют не сам градиент (антиградиент), а его проекцию на поверхность ограничений, точнее, на плоскость, аппроксимирующую эту поверхность в текущей точке. Очевидно, что проекция градиента определяет направление наискорейшего изменения функции на поверхности ограничений.
Приведем один из вариантов метода проектирования градиента сначала для задачи с ограничениями-равенствами, а затем для общего случая. Метод применим, если целевая функция и все функции ограничений дифференцируемы.
Пусть ограничения заданы в виде
![]() (4.55)
(4.55)
Найдем возможное направление l, на котором скорость изменения целевой функции максимальна:
![]() (4.56)
(4.56)
В допустимой области D функции j постоянны. Поэтому искомое направление должно удовлетворять системе равенств
![]() (4.57)
(4.57)
Из связи направления с координатами следует
![]()
что перепишем в виде
![]() (4.58)
(4.58)
Таким образом, для нахождения наилучшего возможного направления необходимо решить задачу оптимизации (4.56)–(4.58). Поскольку условия имеют вид равенств, а функции дифференцируемы, для решения этой вспомогательной задачи воспользуемся методом Лагранжа.
Запишем функцию Лагранжа:
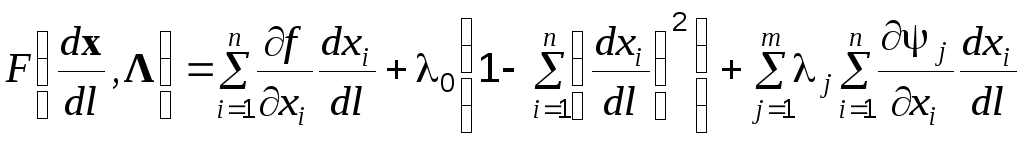 .
(4.59)
.
(4.59)
Неизвестными в
ней являются векторы
![]() и.
Взяв производные
и.
Взяв производные 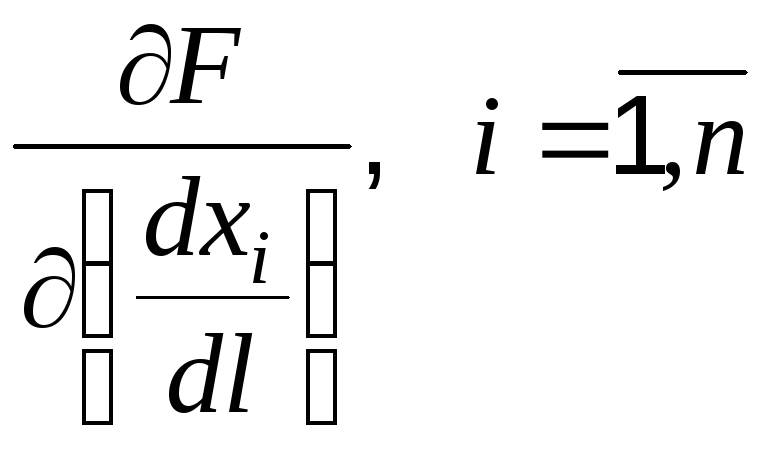 и приравняв
их нулю, получаем
и приравняв
их нулю, получаем
![]()
Отсюда выразим компоненты искомого вектора:
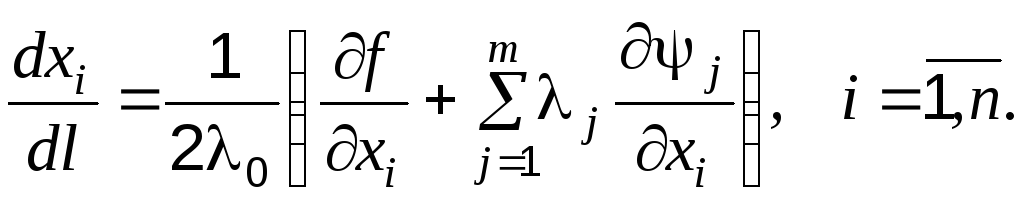 (4.60)
(4.60)
Подставив уравнение (4.60) в формулу (4.58), находим
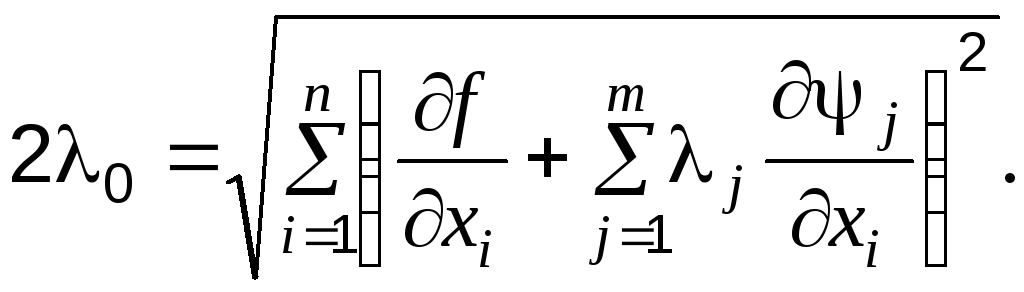
С учетом этого выражения формула (4.60) принимает вид
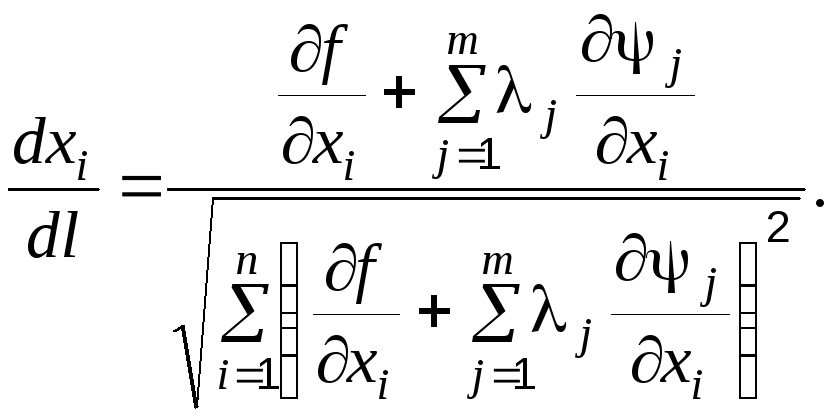 (4.61)
(4.61)
Для определения неизвестных множителей j воспользуемся системой (4.57). Подставив в нее формулу (4.61), получаем
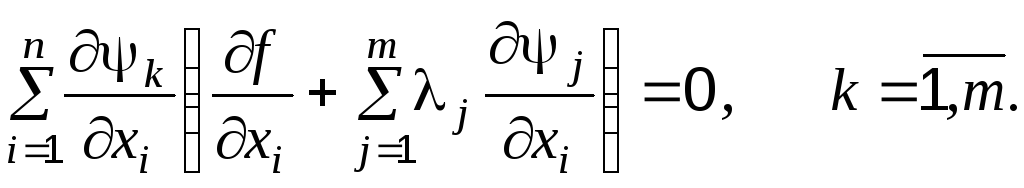
После раскрытия скобок окончательно имеем
![]() (4.62)
(4.62)
Так как направление ищется в конкретной точке, то все производные в уравнении (4.62) – известные константы. Поэтому система уравнений (4.62) является линейной системой относительно j. Ее решение не вызывает затруднений (при условии, что матрица системы не является особенной). Найдя значения j и подставив их в формулу (4.61), получаем компоненты проекции градиента (в знаменателе (4.61) имеем длину проекции градиента). Движение осуществляется в направлении, противоположном проекции.
Аналогично градиентному методу новая точка вычисляется по формуле
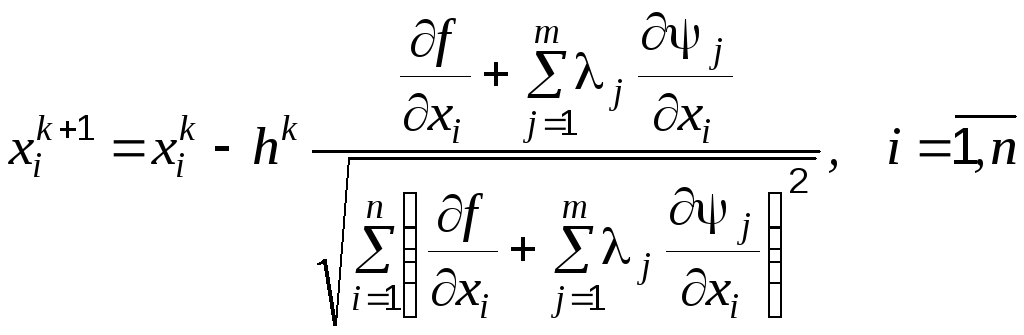 .
(4.63)
.
(4.63)
Алгоритм
Задать начальную точку, удовлетворяющую системе (4.55), начальное значение h0 и точность по величине проекции градиента .
В текущей точке вычислить градиенты всех функций (f и j) и решить систему (4.62).
Вычислить проекцию градиента по формуле (4.61).
Проверить: если
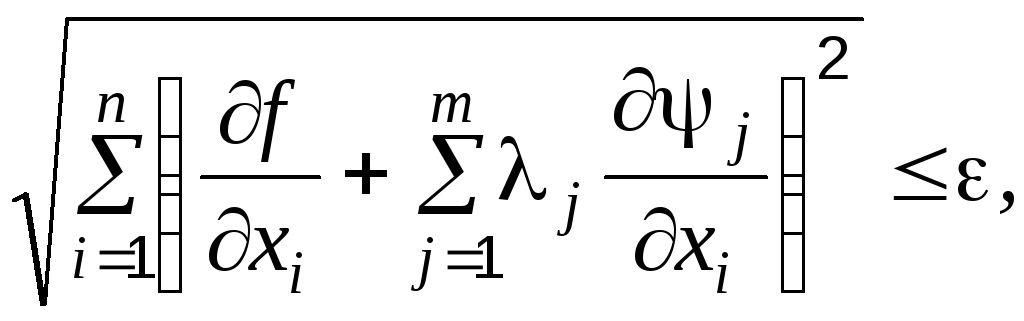 завершить поиск.
завершить поиск.Вычислить новую точку по формуле (4.63).
Проверить: если значение целевой функции улучшилось, перейти на п. 2, иначе уменьшить hk в два раза и перейти на п. 5.
Качественный характер работы алгоритма иллюстрирует рис. 4.38. Здесь функции зависят от 2 переменных, поэтому в каждой точке на линии ограничения может быть всего 2 направления, лучшее из которых определяет проекция градиента. В многомерной задаче таких направлений бесконечное множество.
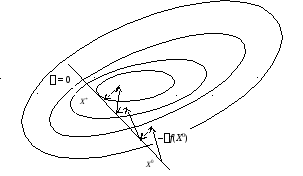
Рис. 4.38. Качественный характер работы алгоритма
При линейных ограничениях могут возникать проблемы поиска лишь при очень малых значениях градиентов функций ограничений и совпадении их направлений, так как это приводит к вырожденности матрицы системы (4.62).
В случае нелинейных
ограничений движение на основе линейной
аппроксимации нарушает равенства.
Поэтому в алгоритм необходимо внести
изменения, обеспечивающие выполнение
равенств с необходимой точностью .
С этой целью алгоритм дополняется
проверкой величины невязки, которая
выполняется в каждой новой точке. Если
![]() ,
то включается процедура коррекции,
состоящая в минимизации невязки:
,
то включается процедура коррекции,
состоящая в минимизации невязки:
![]() (4.64)
(4.64)
Для решения задачи (4.64) можно применить любой метод безусловной оптимизации, но в данном контексте целесообразен метод градиентов. При этом значения (n – m) переменных фиксируются, так как для выполнения равенств достаточно m переменных. Понятно, что при частых коррекциях трудоемкость алгоритма значительно возрастает.
Т еперь
рассмотрим случай, когда ограничения
заданы в виде неравенствj(x)
0. Поиск начинается из точки, в которой
удовлетворяются все ограничения. Пока
они выполняются как строгие, движение
осуществляется по
градиентному методу. Когда достигается
граница допустимого множества,
одно или несколько ограничений
обращаются в равенства. Такие
ограничения называют активными.
В точках с активными ограничениями
направление движения определяется
по проекции градиента на
поверхность этих ограничений,
т.е. применяется вышеприведенный
алгоритм. Пример поиска минимума
при двух линейных неравенствах
показан на рис. 4.39.
еперь
рассмотрим случай, когда ограничения
заданы в виде неравенствj(x)
0. Поиск начинается из точки, в которой
удовлетворяются все ограничения. Пока
они выполняются как строгие, движение
осуществляется по
градиентному методу. Когда достигается
граница допустимого множества,
одно или несколько ограничений
обращаются в равенства. Такие
ограничения называют активными.
В точках с активными ограничениями
направление движения определяется
по проекции градиента на
поверхность этих ограничений,
т.е. применяется вышеприведенный
алгоритм. Пример поиска минимума
при двух линейных неравенствах
показан на рис. 4.39.
Очевидно, что при смешанных и нелинейных ограничениях алгоритм весьма существенно усложняется и требует большого объема вычислений. Поэтому метод проектирования градиентов целесообразно применять при линейных ограничениях.
