
- •Д.В. Астрецов, м.П. Трухин общая теория связи
- •210700 «Инфокоммуникационные технологии и системы связи»
- •Cодержание
- •Общие требования при прохождении лабораторного практикума
- •Характеристика системы моделирования matlab и пакета визуального моделирования simulink
- •Дискретизация и восстановление Непрерывных сигналов
- •1. Цель работы:
- •2. Теоретические основы дискретизации сигналов:
- •3. Описание лабораторной установки:
- •4. Домашняя подготовка к лабораторной работе:
- •5. Экспериментальная часть:
- •6. Содержание отчёта:
- •7. Контрольные вопросы:
- •Амплитудная модуляция
- •1. Цель работы:
- •2. Элементы теории модуляции:
- •Амплитудно-модулированный сигнал записывается в виде
- •В цепь затвора транзистора vт поступает сумма трёх напряжений
- •Как видно из (4), статическая модуляционная характеристика выражается формулой:
- •3. Характеристика лабораторной установки:
- •4. Домашняя подготовка к лабораторной работе:
- •5. Порядок выполнения лабораторной работы:
- •6. Содержание отчёта:
- •7. Контрольные вопросы:
- •Детектирование амплитудно-модулированных сигналов
- •1. Цель работы:
- •2. Элементы теории детектирования Амплитудно-модулированных сигналов:
- •3. Характеристика лабораторной установки:
- •4. Домашняя подготовка к лабораторной работе:
- •5. Порядок выполнения лабораторной работы:
- •6. Содержание отчёта:
- •7. Контрольные вопросы:
- •7.12. Изобразить структурную схему модели диодного детектора и пояснить на ней работу узлов реального диодного детектора.
- •Исследование функций автокорреляции случайных процессов
- •1. Цели работы:
- •5. Лабораторное задание:
- •Исследование функций взаимной корреляции случайных процессов и их производных
- •2. Некоторые сведения из теории случайных процессов:
- •Функция взаимной корреляции процесса x3(t) и его производной по времениможет быть представлена в виде:
- •3. Характеристика лабораторной установки:
- •Систематические коды и их применение в системах связи с обратном каналом
- •3. Описание лабораторной установки:
- •4. Подготовка к лабораторной работе:
- •5. Лабораторное задание:
- •6. Требования к отчету:
- •7. Контрольные вопросы:
- •Оптимальная фильтрация сигналов Известной формы
- •1. Цель работы:
- •2. Основы теории оптимальной фильтрации детерменированных сигналов в присутствии флуктуационных помех:
- •Удельная мощность помехи на выходе фильтра может быть найдена из выражения
- •3. Характеристика лабораторной установки:
- •4. Подготовка к лабораторной работе:
- •6. Требования к отчету:
- •7. Контрольные вопросы:
- •Исследование lc-автогенератора
- •1. Цель работы:
- •7. Контрольные вопросы:
- •Литература:
Исследование функций взаимной корреляции случайных процессов и их производных
Цели работы:
Исследование функций взаимной корреляции стационарных случайных процессов и их производных, изучение методов аппаратурного корреляционного анализа совокупности случайных процессов.
2. Некоторые сведения из теории случайных процессов:
Функцией взаимной корреляции случайных процессов X(t) и Y(t) называется смешанный центральный момент второго порядка системы двух сечений Х(t1), Y(t2), рассматриваемый как функция моментов времени t1 и t2:
![]() (1)
(1)
где W(x1,y2) – плотность вероятности системы случайных величин X1 и Y2;
x1, y2 – значения сечений X(t1) и Y(t2) соответственно;
mx1, my2 – математические ожидания сечений X(t1) и Y(t2).
В случае стационарных и стационарно связанных случайных процессов X(t) и Y(t) функция взаимной корреляции не зависит от значений моментов времени t1 и t2, а зависит от их разности τ = t1 - t2.
Функция взаимной корреляции Кху(τ) характеризует линейную статистическую связь стационарных и стационарно связанных случайных процессов X(t) и Y(t) в зависимости от их временного сдвига относительно друг друга. В точках, где значения функции взаимной корреляции Кху(τ) равны нулю линейная зависимость Y(t) от X(t) и наоборот отсутствует.
Рассмотрим
основные свойства функции взаимной
корреляции
![]() .
Здесь угловые скобки означают вычисление
математического ожидания. Предполагается
также, что процессыX(t)
и Y(t)
имеют нулевые математические ожидания.
При выборе индексов обозначения функции
Кху(τ)
на первое
место условно ставится опережающий
процесс. Отсюда следует:
.
Здесь угловые скобки означают вычисление
математического ожидания. Предполагается
также, что процессыX(t)
и Y(t)
имеют нулевые математические ожидания.
При выборе индексов обозначения функции
Кху(τ)
на первое
место условно ставится опережающий
процесс. Отсюда следует:
![]() (2)
(2)
Таким образом перемена порядка следования индексов эквивалентна изменению знака переменной τ.
В общем случае функция корреляции Кху(τ) не является ни четной, ни нечетной функцией. Поэтому взаимная спектральная плотность мощности процессов X(t) и Y(t) в общем случае является комплексной функцией.
![]() (3)
(3)
Рассмотрим ряд конкретных функций взаимной корреляции.
В качестве первого примера найдем функцию взаимной корреляции между процессами на выходе и на входе линейной цепи. Выражение, связывающее выходной и входной процессы в указанном выше случае имеет вид:
![]() (4)
(4)
где g(t) – импульсная реакция цепи.
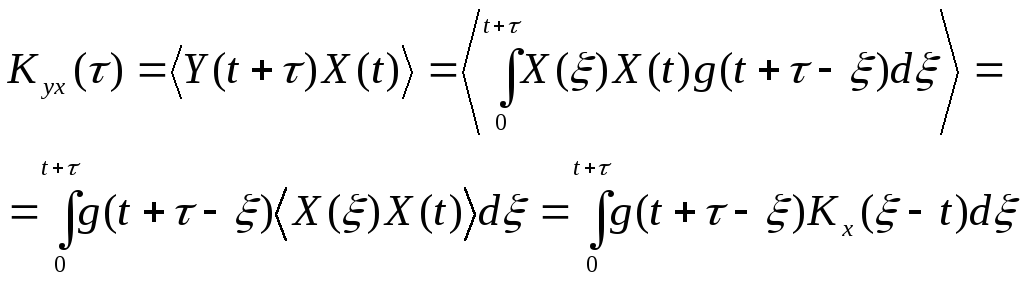 (5)
(5)
Полученное выражение справедливо как для переходного, так и для стационарного режима. В стационарном режиме пределы интегрирования могут быть бесконечными, а функция корреляции не зависит от времени. Тогда:
![]() (6)
(6)
где Кх(τ) – функция автокорреляции входного процесса Х(t).
Таким образом, функция взаимной корреляции стационарных процессов на выходе и входе линейной цепи равна свертке функции корреляции входного процесса и импульсной реакции цепи.
Применяя к левой и правой части (6) преобразование Фурье в форме, представленной равенством (3), можно получить:
![]() (7)
(7)
где Syx(jω) – взаимная спектральная плотность мощности процессов Y(t) и X(t);
K(jω) – коэффициент передачи цепи;
Sx(ω) – спектральная плотность мощности процесса X(t).
Взаимная спектральная плотность мощности входного X(t) и выходного Y(t) процесса может быть получена обращением по Фурье взаимной функции корреляции Kxy(τ), которая связана с Kyx(τ) равенством (2).
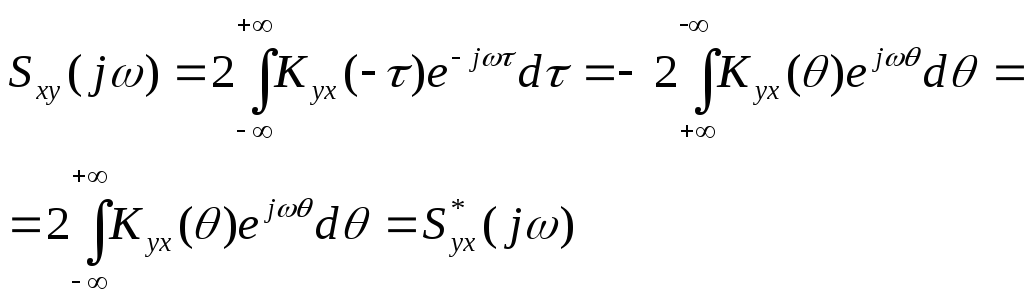 (8)
(8)
где проведена замена переменной интегрирования τ на –θ.
Используя полученное выражение и равенство (7), можно получить выражение для взаимной спектральной плотности процессов на входе и выходе линейной цепи:
![]() (9)
(9)
Полученные результаты можно использовать для исследования функции взаимной корреляции случайного процесса и его производной по времени.
Как известно из теории цепей, коэффициент передачи дифференцирующей цепи, процесс на выходе которой равен производной входного процесса, можно представить выражением:
![]() (10)
(10)
В
этом случае функция взаимной корреляции
производной случайного процесса
![]() и исходного процессаX(t)
может быть записана в виде:
и исходного процессаX(t)
может быть записана в виде:
 (11)
(11)
Таким образом, функция взаимной корреляции между производной и случайным процессом равна производной функции корреляции случайного процесса.
Отметим
основные свойства функции взаимной
корреляции
![]() ,
где
,
где![]() – производная процессаX(t).
– производная процессаX(t).
Известно, что функция корреляции Kx(τ) стационарного случайного процесса является чётной функцией τ и в точке τ=0 имеет максимум, равный дисперсии. Следовательно, функция взаимной корреляции
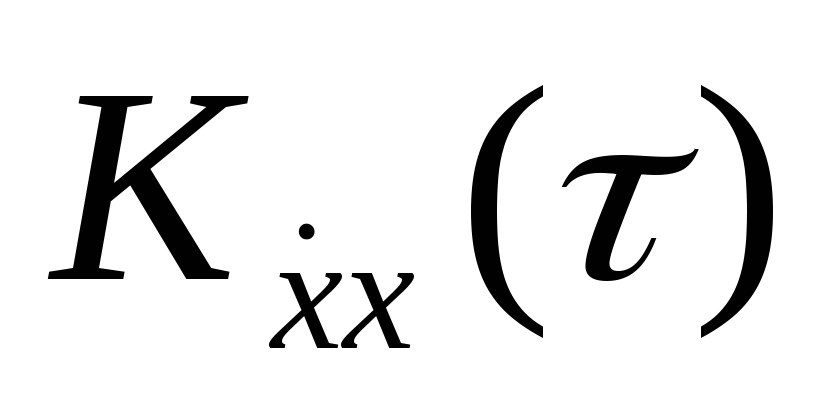 является нечетной функцией и
является нечетной функцией и ,
то есть в одинаковые моменты времени
стационарный процесс и его производная
не коррелированны, а в случае нормального
распределенияX(t)
и независимы.
,
то есть в одинаковые моменты времени
стационарный процесс и его производная
не коррелированны, а в случае нормального
распределенияX(t)
и независимы.Если функция корреляции Kx(τ) недифференцируемая, то случайный процесс X(t) считается недифференцируемым.
В связи с тем, что функция Kx(τ) в начале координат максимальна, то ее производная при τ = 0 равна нулю. Поэтому при монотонном характере функции корреляции Kx(τ) при τ > 0 ее производная отрицательна, а при τ < 0 положительна. В силу того, что функция корреляции Kx(τ) является четной, то функция
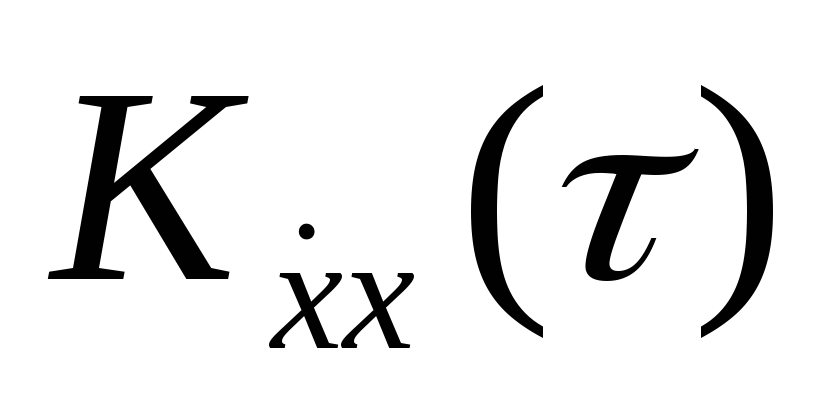 не четна. При увеличении абсолютного
значенияτ
функция взаимной корреляции
не четна. При увеличении абсолютного
значенияτ
функция взаимной корреляции
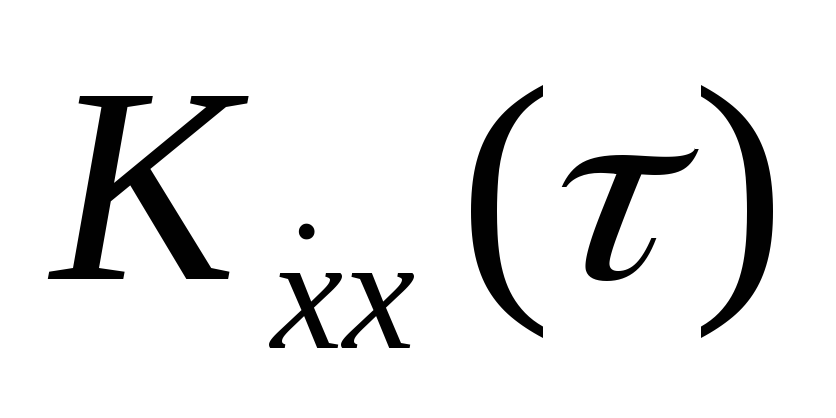 стремится к нулю.
стремится к нулю.
Рассмотрим функции взаимной корреляции случайных процессов на выходах цепей б) и в) лабораторной работы № 4 (см. рисунок 2 работы № 4) и их производных. Принципиальные схемы цепей б) и в) представлены на рисунке 1.
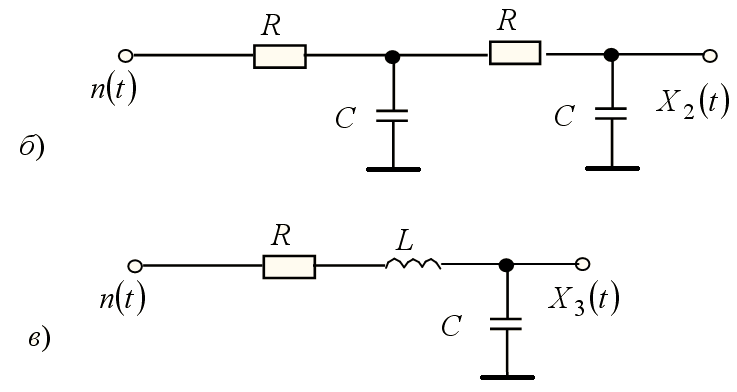
Рисунок 1 – Принципиальные схемы цепей, формирующих
случайные процессы X2(t) и X3(t)
Резистор R в цепи в) может быть замкнут специальным проводником.
Нормированные корреляции процессов X1(t) и X3(t) имеют вид:
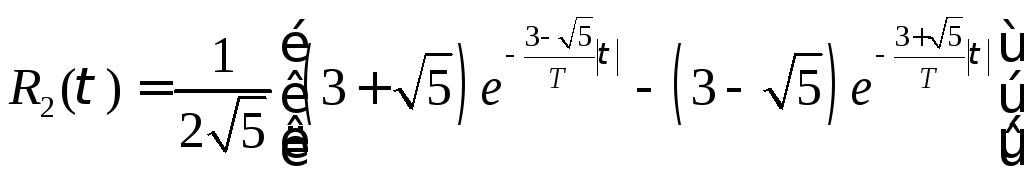 (12)
(12)
где T=RC;
![]() (13)
(13)
где
![]() ,
,![]() ,
,![]() ,
,
r – сопротивление потерь в катушке индуктивности цепи в).
Равенство (13) получено в предположении, что резистор R замкнут (на схеме рисунка 1,в отсутствует).
Аналогично,
функция взаимной корреляции случайного
процесса X2(t)
и его производной по времени
![]() равна:
равна:
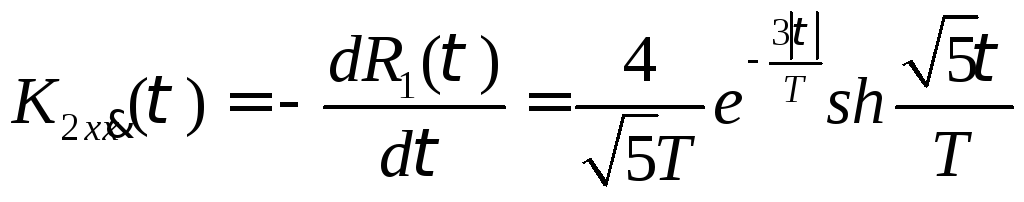 (14)
(14)
где
![]() – функция гиперболического синуса.
– функция гиперболического синуса.
