Розділу 3 в тій книжці нема. В неті теж нема 

IV Обчислювальні методи та елементи математичної статистики

4. Оцінки вищих момент них функцій

V Математичне моделювання теплопровідності твердих тіл

1. Коефіцієнт теплопровідності.

2. Тепловий потік через довільну поверхню

3. Ізотермічні поверхні

4. Теплопровідність ізотопних тіл

5. Диференціальне рівняння теплопровідності для ізотопного тіла

6. Диференціальне рівняння теплопровідності для рухомого середовища

7. Перетворення координат

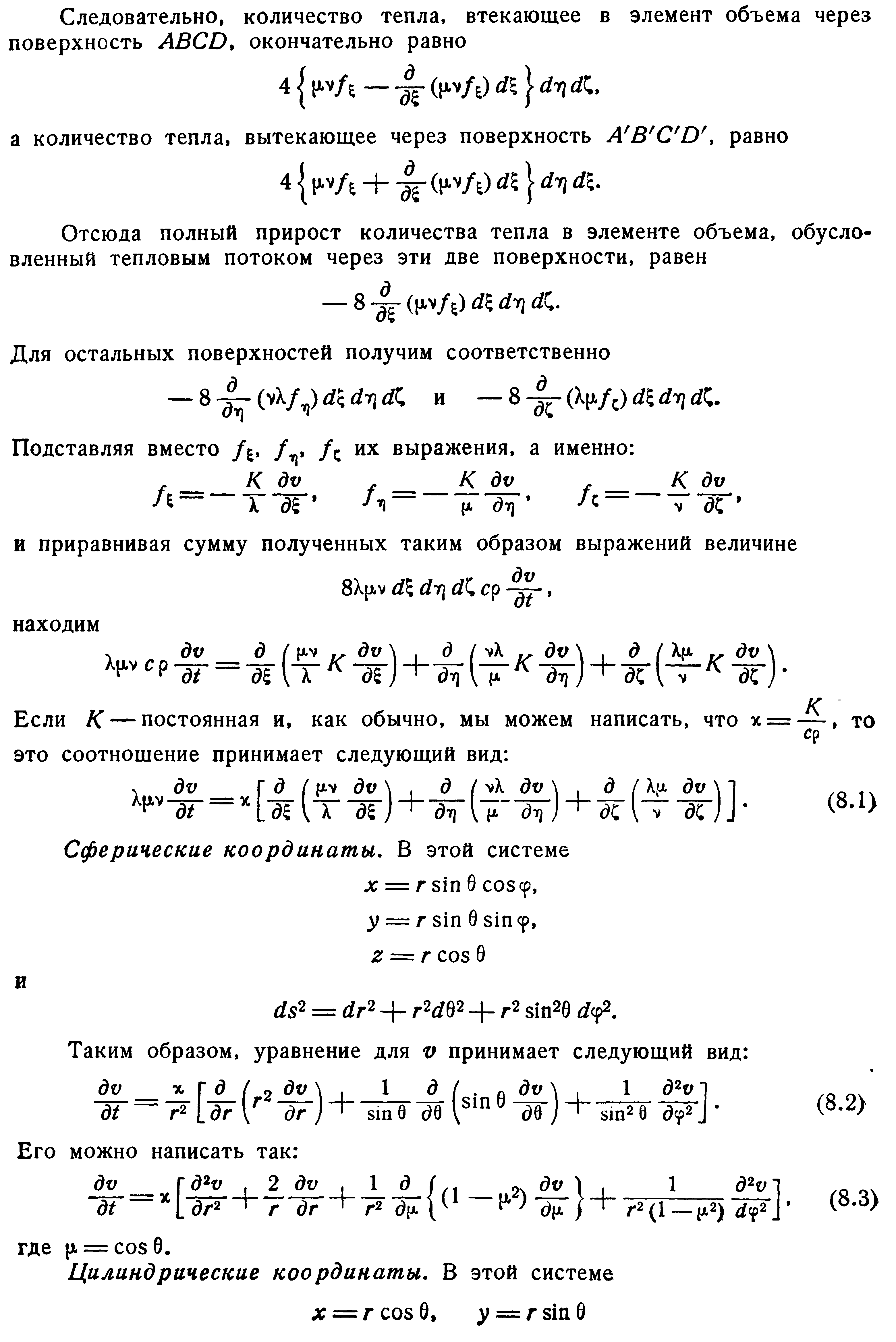
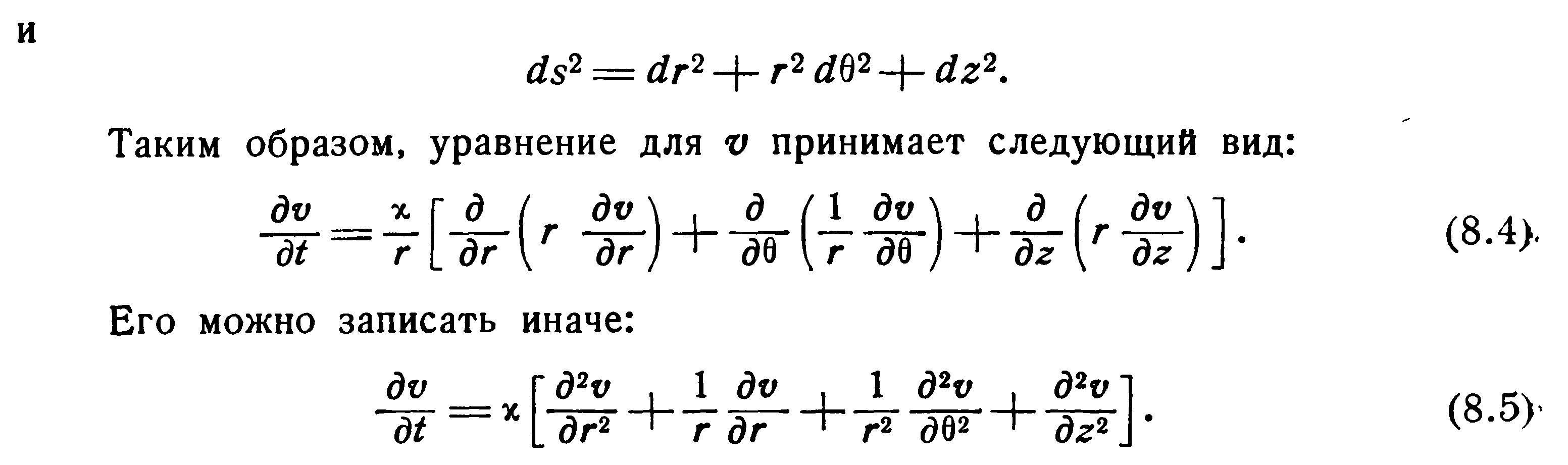
8. Початкові і граничні умови

9. Експериментальні методи визначення теплопровідності

10. Математичне моделювання диференціальних рівнянь поширення температури в феромагнітному твердому тілі.

Теплопроводности уравнение

        дифференциальное уравнение (См. Дифференциальные уравнения) с частными производными параболического типа, описывающее процесс распространения теплоты в сплошной среде (газе, жидкости или твёрдом теле); основное уравнение математической теории теплопроводности (См. Теплопроводность). Т. у. выражает тепловой баланс для малого элемента объёма среды с учётом поступления теплоты от источников и тепловых потерь через поверхность элементарного объёма вследствие теплопроводности. Для изотропной неоднородной среды Т. у. имеет вид:

        

        ,

        где ρ — плотность среды; c_v — теплоёмкость среды при постоянном объёме; t — время; х, у, z — координаты; Т = Т (х, у, z, t) — температура, которая вычисляется при помощи Т. у.; λ — коэффициент теплопроводности; F = F (x, y, z, t) — заданная плотность тепловых источников. Величины ρ, C_v, λ зависят от координат и, вообще говоря, от температуры. Для анизотропной среды Т. у. вместо λ содержит Тензор теплопроводности λ_ir, где i, k = 1, 2, 3.

         В случае изотропной однородной среды Т. у. принимает вид:

        

        ,

        где ΔT — Лапласа оператор, a² = λ/(ρc_v) — коэффициент температуропроводности; f = F/(ρc_v). В стационарном состоянии, когда температура не меняется со временем, Т. у. переходит в Пуассона уравнение ΔТ = f/a² = F/λ или, при отсутствии источников теплоты, в Лапласа уравнение ΔТ = 0. Основными задачами для Т. у. является Коши задача и смешанная краевая задача (см. Краевые задачи).

однородное дифференциальное уравнениес частными производными

Это уравнение является простейшим представителем параболического типа уравнений. При n=3 оно описывает процесс распространения тепла в твердом теле. К основным корректно поставленным задачам для Т. у. относятся первая краевая задача(в цилиндрич. области) и задача Коши - Дирихле (в полупространстве). Решение последней задачи выписывается в явном виде:

где - заданная непрерывная равномерно ограниченная вфункция.

Вывод уравнения теплопроводности:

Рассмотрим задачу о распространении тепла в неревномерно нагретом твердом теле. В качестве величины, характеризующей процесс, возьмем температуру u(M,t), где M = M(x,y,z) - некоторая точка внутри рассматриваемого тела.

Посмотреть определения потока и дивергенции векторного поля

1) Будем рассматривать процесс распространения тепла посредством теплопроводности (т.е. при непосредственном контакте областей с разной температурой).

2) Для теплообмена посредством теплопроводности необходимо наличие ненулевого температурного градиента, т.е. различные части тела должны иметь разную температуру. При этом, так как каждая система стремится к своему равновесному состоянию, происходит переток тепла от более "нагретых" частей тела к более "холодным".

3) Для математического описания полей тепловых потоков введем в рассмотрение вектор плотности теплового потока , имеющий направление от более "горячих" участков тела к более "холодным", а по величине равный количеству тепла, проходящему через единицу поверхности за единицу времени:.

4) В основе аналитической теории теплопроводности лежит экспериментально установленный закон Фурье, согласно которому , гдеλ - коэффицент теплопроводности среды (равен количеству тепла, переносимого в единицу времени через единицу поверхности при градиенте температуры , равном единице).

5) Будем считать, что наше изучаемое тело изотропно, т.е. λ = λ(x,y,z) и не зависит от выбора нормали к поверхности; .

6) По определению потока для вектора можем записать.

При этом получим: если тело отдает тепло, то ; если получает, то. Условимся в дальнейшем для определенности считать поток теплаdQ_s, направленный внутрь тепла положительным. Для этого в определение потока введем знак "-" (минус). Тогда элементарный поток через поверхность dS за время dt: , и через всю поверхностьS, ограничивающую объем S за время .

(1)  

7) Предположим, что внутри нашего объема есть источники тепла. Обозначим через F(M,t) - плотность тепловых источников (количество тепла, выделяемое в единице объема за единицу времени). Тогда во всем объеме V за время выделитсяQ_V количества тепла: [для элементарного объема dV выделяемое количество тепла dQ_V = F(M,t)dVdt]:

(2)   .

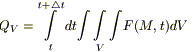8) В соответствии с 1^м началом термодинамики тепло, получаемое системой идет на изменение ее температуры и на совершение этой системой работы: Q = Cdu + δA. Будем считать, что δA = 0 (для твердых тел).

du - изменение температуры за время в точкеМ: 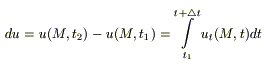  (по теореме о конечных приращениях).

C - теплоемкость объема V, может быть расписана через удельную теплоемкость с, плотность вещества p и объем V: C_dV = c(M)(M)dV - для элементарного объема dV. Тогда

(3)   - для объемаV.

В наш выделенный объем тепло δQ поступает за счет 2^x механизмов: переноса тепла через поверхность, и возникновения тепла за счет работы источников).

Q = Q_s + Q_V; т.е. Cdu = Q_s + Q_V.

Подставим (1), (2), (3):  

Применим теорему о среднем значении (дважды: по t и по V) к каждому из этих интегралов:

Поделим полученное соотношение на () и перейдем к пределу при, так какt₁ - любое время (могли вместо t₁ и t₂ взять t и ); получим уравнение, описывающее изменение температуры в любой точке М в любое времяt.

(1)   или

  - уравнение теплопроводности.

Если среда однородна, то λ,c,p - const и λ можно вынести из под функции div,и, поделив на (cp), получим:

(1a)   ,     так как, то

(1б)   - уравнение теплопроводности для однородной среды.

Если , то уравнение будет однородным.

Рассмотрим теперь дополнительные условия, необходимые для однозначного решения задачи:

а) Необходимо знать начальное распределение температуры:

(2)   u(M,0) = φ(M);

б) Тепловой режим на границе. Основные виды тепловых режимов:

1. - на границе поддерживается определенная температура

2. - через границу подается определенный тепловой поток

3. - происходит теплообмен с внешней средой, температура которой известна.

Разберем более подробно каждый из типов:

1. (3а)   u/_s = f₁(P,t), где f₁ - известная функция, P є S; если поддерживается нулевая температура, то u/_s = 0.

2. Обозначим через ν(P,t) - плотность теплового потока на границе S. (Количество тепла, проходящего через единицу площади за единицу времени).

Пусть σ - произвольный участок поверхности S, ограниченный замкнутой гладкой кривой.

Рассмотрим объем V в виде прямого цилиндра с основанием σ и высотой h; второе основание - σ ₁ - есть поверхность параллельная σ ().

Для записи 1^го начала термодинамики (закон сохранении энергии):

Cdn = dQ;

;

;

;

.

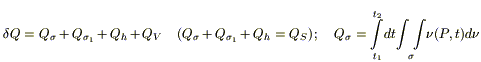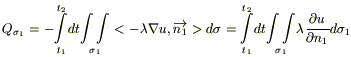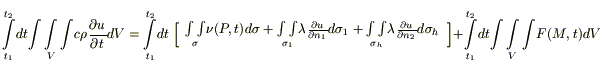при интегралы поV, а также интеграл по , при этом так каки.

Применяя дважды теорему о среднем (по t и по σ), устремляя , получаем:

(3б)  

Если поверхность S теплоизолирована (ν = 0):  

3. Будем считать, что теплообмен между телом и окружающей средой происходит по закону Ньютона: плотность теплового потока ν(P,t), получаемого из внешней среды, пропорциональна разности температуры окружающей среды θ(t) и температуры u внутри V вблизи поверхности S.

( * )  ν(P,t) = H(θ(t) - u(P,t))   P є S (H - коэффициент теплообмена).

Таким образом, мы имеем случай II, где ν(P,t) имеем специфический вид (*), т.е. ;

(3в)  .

В случае, если температура окружающей среды θ(t) = 0, получим однородное граничное условие 3^го рода:   .

Таким образом, мы приходим к задаче: найти решение уравнения теплопроводности (1), удовлетворяющее нормальным условиям (2) и одному из граничных условий (3). Совершенно аналогично ставятся задачи в одномерном и двумерном случаях. Для уравнения (1) можно также поставить задачу Коши (т.е. задачу без граничных условий)

Замечание: к уравнению (1) приводятся и другие физические задачи: уравнение диффузии, движение вязкой жидкости.

Уравнения эллиптического типа.

В частном случае, когда температура u(M,t) не меняется со временем (установившаяся температура) u = u(x,y,z), уравнение (1) [так как u_t тождественно равно 0] принимает вид:

(4)    ;

если λ - const:   - уравнение Пуассона, а при отсутствии источников тепла:

(5)    приλ = 0 - уравнение Лапласа.

Для однозначного определения температуры не надо знать ее начальное распределение, а достаточно лишь знать тепловой режим на границе S.

В результате для уравнений эллиптического типа приходим к следующим задачам:

найти решение уравнений (4) или (5) с граничными условиями (3), в которых функции f₁, f₂, f₃ не зависят от времени. Соответствующие краевые задачи (по граничным условиям) называются задачей Дирихле, задачей Неймана и задачей Робена.