II Математичні моделі випадкових процесів

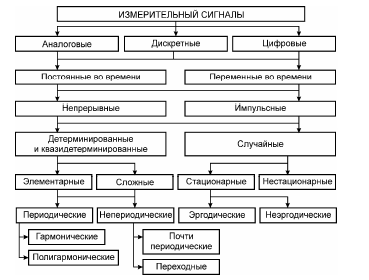
11. Адитивна та мультиплікативні моделі стохастично періодичних сигналів, їх властивості.

Любой нестационарный случайный процесс представляет собой композицию детерминированных и стационарной составляющих. Чаще всего в инженерной практике встречаются процессы, которые можно представить в виде аддитивной, мультипликативной или аддитивно- мультипликативной модели. Если на основе имеющихся экспериментальных данных можно установить класс нестационарного процесса, то для его исследования нет необходимости производить анализ по ансамблю, а можно оценить его параметры по одной реализации.

Задача определения математического ожидания случайного процесса идентична задаче сглаживания случайной составляющей процесса, которая предполагается стационарной. При выборе того или иного метода обработки данных, необходимо исходить из возможности получения несмещенных, эффективных и состоятельных оценок математического ожидания, простоты реализации алгоритма обработки и возможности проведения анализа в реальном масштабе времени. Перечисленным требованиям, в частности, удовлетворяет оператор текущего среднего.

В качестве меры погрешности оценки математического ожидания можно использовать среднюю квадратическую ошибку (СКО), которая определяется как квадратный корень из суммы квадрата ошибки смещения оценки и ее дисперсии.

Для процессов нестационарных по математическому ожиданию (аддитивная и аддитивно-мультипликативная модели) ошибка смещения оценки математического ожидания определяется только аддитивной детерминированной составляющей. Рассмотрим эти модели:

аддитивная         X(t) =j₁(t) +z(t);

аддитивно-мультипликативная     X(t) =j₁(t) +j₂(t)*z(t),

где z(t) - стационарный случайный процесс с нулевым математическим ожиданием и единичной дисперсией; j₁(t), j₂(t) - детерминированные функции времени.

Ошибка смещения для непрерывного процесса:

e_см(t) = j₁(t) - 1/Т * т_t ^t+Tj₁(t)*dt.

Для типовых детерминированных зависимостей она легко определяется. Например, если j₁(t) - линейная функция, то в середине интервала сглаживания e_см(t+T/2) равна нулю. Если j₁(t)=sin(2*p*f*t), то в середине интервала сглаживания e_см(t+T/2) = sina(t+T/2)*[1 - (sinaT/2)/(aT/2)], где a=2pf. В операторе текущего среднего каждая точка отсчета, за исключением крайних, заменяется средним значением на интервале сглаживания, поэтому приведенные формулы можно использовать для вычисления ошибки смещения практически в каждой точке реализации. Интервал усреднения должен быть меньше периода j₁(t), так как в противном случае ошибка смещения соизмерима со значениями детерминированной составляющей, определяющей математическое ожидание процесса. В докладе рассмотрено влияние закона изменения дисперсии на выбор оптимального интервала усреднения для процессов, у которых математическое ожидание и дисперсия являются функциями времени. При этом были получены результаты, которые позволяют сделать заключение о том, что законы изменения дисперсии практически не влияют на выбор интервала усреднения.

Сигналы. Сигналом назовем изменяющуюся физическую величину, отображающую сообщение. Известно, что реальные сигналы всегда являются действительными функциями времени. Произвольный сигнал запишется в виде

(1.3)

огибающая А(t) и фаза θ(t) определяются с помощью соотношений

(1.4)     

где υ(t) – сигнал, комплексно-сопряженный с u(t).

          Фаза сигнала связана с его мгновенной частотой ω(t) и может быть записана

                                      (1.5)

где ω₀- несущая частота, φ(t)- в общем случае нелинейное слагаемое, β- начальная фаза.

Таким образом, произвольный сигнал

(1.6)

          Помехи. Помехи, искажающие сигнал, подразделяют на аддитивные и мультипликативные (модулирующие). Аддитивной помехой n(t) называется такая помеха, которая входит в смесь сигнала с помехой в качестве слагаемого

(1.7)

Для неаддитивных помех смесь сигнала с шумом запишется

(1.8)

где ν(t)- мультипликативная помеха.

Наиболее важной из аддитивных помех является собственный шум радиоприемного устройства, всегда присутствующий на его входе. Шум является случайной функцией времени и его можно считать стационарным случайным процессом. Собственный шум обладает равномерным энергетическим спектром во всем диапазоне частот от 0 до бесконечности. Такой шум называют белым.

          Наличие шума, уменьшает достоверность приема сообщений, количество информации уменьшается (информация разрушается). Разрушение информации может быть следствием действия еще различного рода помех: естественных, взаимных и намеренных. Естественные помехи – входные тепловые и дробовые шумы приемника, отражения радиосигналов от природных образований (суши, моря и т.п.), излучения Солнца или иных внеземных источников. Взаимные – мешающие сигналы, возникающие на входе приемного устройства из-за излучения других радиотехнических устройств, также производящие полезную передачу или извлечение информации. Намеренные – создаются сознательно с целью воспрепятствовать получению противником полезной для него информации.

13. Періодичні випадкові процеси та їх моментні функції

http://ena.lp.edu.ua:8080/bitstream/ntb/11248/1/02.pdf

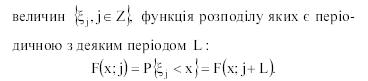
http://archive.nbuv.gov.ua/portal/chem_biol/nvnltu/21_7/322_Dem.pdf

http://posibnyky.vntu.edu.ua/e_s/33.htm

Одним із найпростіших підкласів циклічних випадкових процесів є випадкові процеси, що утворені шляхом адитивного поєднання детермінованої числової циклічної функції та стаціонарного випадкового процесу, зокрема білого шуму.

14. Процеси з незалежними приростами та періодичні білі шуми

http://www.imath.kiev.ua/deppage/stochastic/people/Gusak/AAA.pdf

______________________

15. Моделі дискретних стохастично періодичних сигналів

http://ena.lp.edu.ua:8080/bitstream/ntb/11248/1/02.pdf

16. Дискретні періодичні білі шуми та їх класифікація.

Теорема 1. Якщо для лінійного випадкового процесу

(4)

ядро якого а породжуючий процесє процесом з незалежними-періодичними приростами, то лінійний процес (4) буде-періодичним, тобто періодичною буде його багатовимірна функція розподілу, або це еквівалентно тому, що періодичним буде логарифм його багатовимірної характеристичної функції (3):

Якщо процес (4) записати у вигляді де- узагальнена похідна від процесу з незалежними- періодичними при-ростами, тобто є періодичний білий шум, то в цьому випадку результат теореми має наглядну ілюстрацію, приведену на рис. 4, де показано періодичний білий шум, що поступає на лінійну систему з імпульсною реакцією. При цьому на виході системи спостерігається випадковий періодичний процес.

Дискретні періодичні білі шуми (п.б.ш.)
Білі шуми з дискретними розподілами	Білі шуми з неперервними розподілами
Бернуллі п.б.ш.	рівномірний п.б.ш.	п.б.ш.
біноміальний п.б.ш.	трикутний п.б.ш.	п.б.ш.
геометричний п.б.ш.	показниковий п.б.ш.	Стьюдента п.б.ш.
Пуассона п.б.ш.	нормальний п.б.ш.	п.б.ш.
логарифмічний п.б.ш.	гама п.б.ш.	логістичний п.б.ш.

17. Ковзне середнє при дії періодичного білого шуму

http://wiki.tntu.edu.ua/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%BA%D0%BE%D0%B2%D0%B7%D0%BD%D0%BE%D0%B3%D0%BE_%D1%81%D0%B5%D1%80%D0%B5%D0%B4%D0%BD%D1%8C%D0%BE%D0%B3%D0%BE

Ковзне середнє (англ. Moving Average - MA) – інструмент згладжування часових рядів, застосовуваний головним чином для відображення змін біржових котирувань акцій, цін на сировину і так далі. MA – один з найстаріших і найбільш поширених інструментів технічного аналізу. MA показує середнє значення ціни за певний період часу.

Види ковзних середніх

Існує декілька видів ковзних середніх:

• просте ковзне середнє (SMA);

• експоненційне ковзне середнє (EMA);

• зважене ковзне середнє (WMA);

• трикутне ковзне середнє (TMA);

• адаптивне ковзне середнє (AMA);

• синус-зважене ковзне середнє (SWMA);

• ковзне середнє кінцевої точки (EPMA);

• та інші, менш поширені.

з яких найбільш поширеними є перші три.

Просте ковзне середнє

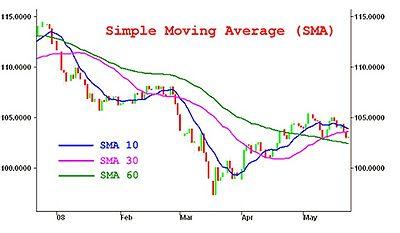
SMA за значенням коефіцієнта згладжування (10, 30 і 60)

Просте ковзне середнє (англ. Simple Moving Average – SMA) – є одними з найбільш простих і популярних індикаторів в технічному аналізі. SMA є звичайним середнім арифметичним від цін за певний період. SMA відноситься до класу індикаторів, які слідують за трендом, воно допомагає визначити початок нової тенденції і її завершення, за його кутом нахилу можна визначити силу (швидкість руху), воно ж в якості основи (або згладжуючого фактора) застосовується у великій кількості інших технічних індикаторів. Іноді ковзне середнє називають лінією тренда.

Формула простого ковзного середнього:

де – ціни на ринку;

n – основний параметр – довжина згладжування або період SMA (кількість цін що входять у розрахунок ковзного). Іноді цей параметр називають порядком змінного середнього.

Просте ковзне середнє є звичайним середнім арифметичним від цін за певний період. SMA являє собою якийсь показник ціни рівноваги за певний період, чим коротше SMA, тим за менший період береться рівновага. Усереднюючи ціни, воно завжди слідує за головною тенденцією ринку, фільтруючи дрібні коливання. Чим менший параметр SMA (коротке ковзне середнє), тим швидше воно визначає нову тенденцію, але й одночасно робить більше помилкових коливань, і навпаки чим більший параметр (довге ковзне середнє), тим повільніше визначається новий тренд, але надходить менше помилкових коливань.

Недоліки методу ковзного середнього

При використанні методу SMA для торгівлі по тренду запізнювання на вході і на виході з тренда як правило дуже значне, тому в більшості випадків втрачається велика частина трендового руху.

Один з найбільш серйозних недоліків методу SMA, полягає в тому що воно надає однакові ваги як новими цінами, так і більш старими, хоча логічніше було б припустити, що нові ціни важливіші, тому що відображають більш близьку ринкову ситуацію до поточного моменту.

Зважене ковзне середнє

Зважене ковзне середнє (англ. Weighted Moving Average – WMA). Одним з недоліків SMA є присвоєння при його розрахунку всім цінам однакових ваг при усередненні незалежно від того, ближче чи далі вони від поточного моменту. Цей недолік усунуто у зваженому ковзному середньому. WMA, таким чином, є звичайною модифікацією SMA з вагами підібраними так, що останні ціни мають більшу вагу.

Зважене ковзне середнє визначається за формулою:

де – значення ціниi-періодів тому, (i сьогодні = 1);

–значення ваг для ціни i-періодів тому.

Зважене ковзне середнє являє собою арифметичне зважене коливань цін за певний період. В якості аналітичного інструменту воно знімає частину недоліків звичайного ковзного, але не усуває їх повністю.

Експоненційне ковзне середнє

Експоненційне ковзне середнє (англ. Exponential Moving Average – EMA) зменшує помилку, надаючи більшу вагу останнім цінами у порівнянні з більш далекими цінами. Цей метод дозволяє більш швидко реагувати на поточні зміни ціни в порівнянні з SMA. Вага, що надається останній ціні, залежить від періоду ковзної середньої. Чим коротший період EMA, тим більша вага надаватиметься останньою ціною.

Експоненційне ковзне середнє може бути визначене двома шляхами – як відсоткове ковзне середнє або як періодичне ковзне середнє. Відповідно в відсотковому ковзному, єдиним параметром є вага (відсоток), а в періодній – період КС.

Основна формула виглядає наступним чином:

де EMA – експонентна ковзна середня;

–значення ціни в i-му періоді;

n – період розрахунку;

–значення ЕМА попереднього періоду.

Необхідно зазначити, що теоретично в розрахунку цієї ковзної використовуються всі ціни, за весь період її побудови і, незважаючи на те, що вплив старих цін зникає з часом, він не зникає до кінця. Ефект старих цін зникає швидше для більш коротких EMA, в порівнянні з більш довгими. На реальному графіку різниця між SMA і EMA не дуже велика, хоча і є присутня. Вважається, що експоненційне ковзне все ж краще відображає ринкові ціни при інших рівних умовах, оскільки вплив кожної попередньї ціни убуває експоненційно з його віддаленістю від поточної ціни.

Лінійні випадкові процеси. Існують різні означення лінійних випадкових процесів. Розглянемо одне із них, що основане на інтегральному зображенні

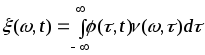, (28)

де - імпульсна характеристика лінійного фільтру;

- білий шум.

Тут лінійний процес розглядається як перетворення білого шумулінійним фільтром з імпульсною характеристикою. При цьому можуть бути одержані лінійні процеси з різними ймовірнісними характеристиками, які визначаються видом функції, а також видом білого шуму. Зокрема, білий шум може бути гаусовим, пуасоновим, їх сумішшю або іншими білими шумами. Лінійний фільтр у виразі (28) має назву формуючого фільтра, а білий шум - породного процесу.Для лінійних процесів з дискретним часом математична модель визначається відповідним співвідношенням

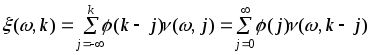(29)

де - дискретні відліки імпульсної характеристики фільтру,- білий шум з дискретним часом.

Лінійний процес можна також зобразити у виді авторегресії на минулі значення. При цьому можна одержати процеси авторегресії, ковзного середнього та змішані процеси авторегресії та ковзного середнього. Зокрема, процес авторегресії -го порядку описується рівнянням

. (30)

Лінійні процеси можуть бути використані як математичні моделі, зокрема, при описі джерела мовних повідомлень, кодера мовних повідомлень, джерела корельованих завад.

Існує також багато інших математичних моделей, що мають свої характерні властивості і дають можливість враховувати особливості різних фізичних процесів в системах зв'язку при їх моделювані на ЕОМ. Зокрема, це математичні моделі, що описують негаусів характер сигналів за допомогою сумішей розподілу, сукупності моментних та кумулянтних функцій, а також нестаціонарний характер сигналів - за допомогою періодично-корельованих випадкових процесів.