Основные свойства неопределенного интеграла

1) ,т.е. производная от неопределенного интеграла равна подинтегральной функции.

Действительно:

2) , т.е. дифференциал от неопределенного интеграла равен подинтегральному выражению.

Действительно:

3) , т.е. неопределенный интеграл от дифференциала функции равен самой этой функции в сумме с некоторой произвольной константой С.

Действительно:

§2. Таблица основных интегралов

Составим таблицу основных интегралов, используя таблицу производных основных элементов функции и учитывая, что:.

Интегралы с 1 по 16 называются табличными. Их надо знать наизусть.

§3. Простейшие правила интегрирования

Докажем основные правила интегрирования:

1. Постоянный множитель можно выносить за знак интеграла:

2. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме их интегралов:

3. 3.Инвариантность формулы интеграла.

Если - произвольная дифференцируемая функция отx.

Доказательство:

Пусть х – независимая переменная,

f(x)– непрерывная функция,

F(x) – её первообразная.

Тогда .

Пусть теперь , где- непрерывная дифференцируемая функция.

Рассмотрим сложную функцию F(u)=

В силу инвариантности формы дифференциала, имеем:

’(u)du =f(u)du

Отсюда, (по свойству 3).

Т.о. формула неопределенного интеграла остаётся справедливой независимо от того, является ли переменная интегрирования независимой или она является функцией от х.

Пользуясь таблицей основных интегралов и правилами интегрирования можно вычислять многие неопределенные интегралы. Этот способ обычно называют непосредственным интегрированием.

Примеры:

При непосредственном интегрировании часто требуется свести данный интеграл к табличному, используя свойства инвариантности формулы интеграла. Эту операцию часто называют «подведение под знак дифференциала», при этом полезно запомнить следующие преобразования дифференциала:

Вообще, f’(x)dx=d(f(x))- эта формула очень часто используется при вычислении интегралов.

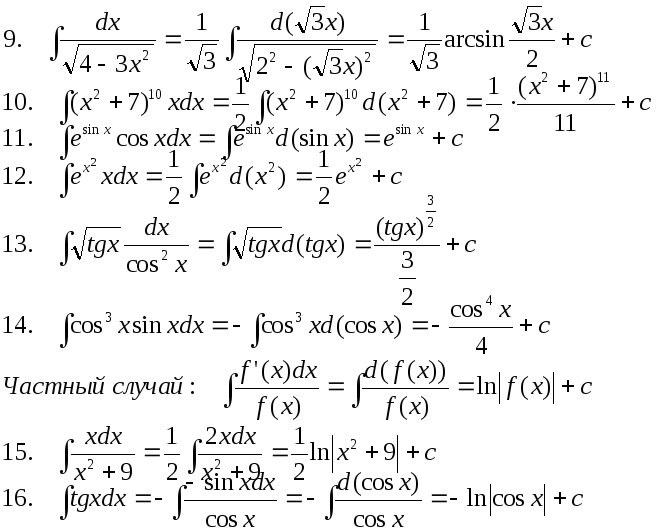
Несколько важных примеров - «неполный квадратный трехчлен (или квадратный двучлен) в знаменателе»:

I)

II)

III)IIIV)

§4. Интегрирование подстановкой (заменой переменной)

Если интеграл непосредственно не вычисляется, то во многих случаях применяют метод интегрирования заменой переменной, заключающийся во введении новой переменной интегрирования (подстановки). При этом заданный интеграл приводится к другому интегралу, который является табличным или к нему сводится (в случае удачной подстановки). Общих методов подбора подстановки не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл . Сделаем подстановкуx=φ(t), гдеφ(t)- непрерывная дифференцируемая функция. Тогдаи на основании свойства инвариантности формулы неопределенного интеграла получаем:

Т.е. (1) - формула замены переменных в неопределенном интеграле.

После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменнойx.

Иногда удобно подбирать подстановку в виде , тогда, где.

Т.е. формулу (1)можно применять справа налево.

Примеры:

1)

2)

3)

Интегрирование выражений, содержащих квадратный трехчлен в знаменателе.

Рассмотрим интегралы:

I)иII)

Для вычисления этих интегралов выполняем следующие действия:

1) выписываем квадратный трехчлен и выражаем из него полный квадрат.

2) произведем замену переменной и получим квадратный двучлен в знаменателе, т.е. сведем интеграл к одному из 4-ех примеров из §3.

Примеры:

1)

2)