Функция l(X) называется функцией Лагранжа.

Согласно этой теореме, чтобы найти точку М₀ условного экстремума функцииf(X), необходимо найтистационарнуюточку функции ЛагранжаL(X)(3), то есть найти частные производные функцииL(X)и решить систему (n + m) уравнений с (n + m) неизвестнымиx₁, x₂, . . . , x_n, l₁, l₂, . . ., l_m:

(4).

Рассмотрим задачу условного экстремума для случая функции двух переменных.

Пусть задана функция двух переменных z = f (x,y)в некоторой областиD. И пусть в этой области задана некоторая линияl: - уравнение связи.

Определение. Условным экстремумом функцииz = f (x,y)называется экстремум этой функции, достигнутый при условии, что переменныеxиyсвязаны уравнением связи .

Замечание:Точки обычного (безусловного) экстремума являются и точками условного экстремума для любой линииl, проходящей через эту точку. Обратное не верно: т.е. точка локального экстремума не обязательно является точкой безусловного экстремума.

Отыскание условного экстремума можно свести к исследованию на обычный экстремум с помощью функции Лагранжа:L(x,y) = f (x,y) +

где - неопределенный постоянный множитель.

Необходимые условия экстремума функции Лагранжа имеют вид:

Из этой системы трёх уравнений можно найти неизвестные x, yи.

Пример:

- полусфера, радиус ееR= 1 и центр – точкаО(0,0),

В точке О(0,0) – экстремум (безусловный максимум) - точкаМ(0,0,1).

Проведем в области Dпрямую АВ, её уравнение:x+y=1 (*)

Найти условный экстремум функции zна прямой (*):x+y-1 = 0

Уравнение (*) – уравнение связи.

Функция Лагранжа для функции и уравнения связи (*):

Имеем:

Необходимые условия экстремума:

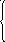Вычтем из первого второе.

x+y= 1

y–x=0

y+x=1 Прибавим к первому второе.

2y= 1

y= . Следовательно, точка (1/2; 1/2;Ö2/2) – стационарная точка для функцииL(x,y,l). Покажем, что точкаС (1/2; 1/2) – точка условного экстремума для функции .

Воспользуемся достаточными условиями экстремума, сформулированными для функции двух переменных в пункте 2 §7.

Поскольку D > 0 иA < 0, то в точкеС () функция имеет максимум: .

Глава 7. Неопределенный интеграл

§1. Понятие неопределенного интеграла

В дифференциальном исчислении решается задача:

По данной функции F(x)найти её производную (или дифференциал):

F’(x)илиdF(x) = F’(x)dx.

В интегральном исчислении решается обратная задача:

Найти функцию F(x), зная её производнуюF’(x) = f (x)или дифференциал

dF(x) = f (x)dx.

Искомую функцию F(x)называютпервообразнойфункцииf(x).

Прямая задача:

Обратная задача:

Определение.Функция F(x) называется первообразной функции f(x) на интервале (а,b), если для любого выполняется условиеF’(x)=f(x) (или dF(x)=f(x)dx) (1)

Например:1)

2)

3)

Очевидно, что если F(x) – первообразная для функцииf(x)на интервале(a,b), то функцияF(x) + C, гдеC=const, также первообразная для функцииf(x)на этом же интервале:.

Отсюда следует, что если функция f(x)имеет хотя бы одну первообразную на интервале(a,b), то она будет иметь б/м первообразных на этом интервале.

Можно показать, что справедлива следующая теорема:

Теорема.Если функцияF(x)является первообразной функцииf(x)на интервале(a,b), то множество всех первообразных дляf(x)задается формулойF(x) + C, гдеC- константа.

Доказательство:

Пусть Ф(x)некоторая другая, отличная отF(x)первообразная функцииf(x), т.е.Ф’(x) = f(x).Тогда для всехимеем(Ф(x) – F(x))’= Ф’(x) – F’(x) = f(x) – f(x) = 0 Ф(x) – F(x) = C, гдеС – константа.

Следовательно: Ф(x) =F(x) +Cч.т.д.

Определение.Множество всех первообразных для функции f(x) F(x) + C называется неопределенным интегралом от функции f(x) и обозначается

- знак интеграла

f(x)– подинтегральная функция

f(x)dx– подинтегральное выражение

х – переменная интегрирования

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых y = F(x) + C.

График каждой первообразной называется интегральной кривой.

Например,

y c₁=1

Y=sinx+1

1 c=0

0 x

Y=sinx

-1

c₂=-1

Y=sinx-1

Замечание:

Для всякой ли функции существует неопределенный интеграл?

Имеет место теорема, утверждающая, что «всякая непрерывнаяна (a,b) функция имеет на этом интервале первообразную», а, следовательно, и неопределенный интеграл.

Итак, ,где F’(x) = f (x)иdF(x) = f (x)dx..

Из этого определения неопределенного интеграла вытекают следующие свойства: