
u_lectures
.pdf
Поверхность конуса сцепления представляет собой геометрическое место максимальных реакций Rmax опорной плоскости. Пространство внутри
конуса сцепления соответствует совокупности возможных положений реакции опорной плоскости в положении равновесия тела.
Следовательно, тело будет
сц |
находиться в равновесии, если реакция |
R |
|||||
R |
опорной |
плоскости |
проходит |
внутри |
или |
||
лежит |
на поверхности конуса сцепления. |
||||||
|
Поэтому, если результирующая активных |
||||||
|
сил Q |
(рис. 7.10) |
образует с |
нормалью к |
|||
Q |
шероховатой поверхности угол |
меньший |
|||||
|
угла сцепления сц, то никакой сколь угодно |
||||||
Рис. 7.10 |
большой силой Q |
нельзя сдвинуть |
тело |
||||
вдоль |
данной |
поверхности. |
Этим |
||||
|
|||||||
объясняются явления заклинивания и самоторможения.
Трение качения
Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.
Рассмотрим круглый цилиндрический каток весом Р радиусом R, лежащий на шероховатой горизонтальной плоскости (рис. 7.11, а).
Приложим к оси катка горизонтальную силу Q меньшую Fпр . Тогда в точке А контакта катка с неподвижной плоскостью возникнет нормальная реакция N и сила сцепления Fсц , которая будет препятствовать скольжению катка по плоскости. При такой схеме качение должно начинаться под действием любой малой силы Q , поскольку пара сил Q, Fсц ничем не
уравновешивается. Однако опыт показывает, что этого не происходит.
В действительности вследствие деформаций тел касание катка с плоскостью происходит по некоторой площадке АВ (рис. 7.11, б). При
действии сдвигающей силы Q интенсивность давления у края В больше чем
у края А. В результате нормальная реакция N (равнодействующая этих давлений) оказывается смещенной на расстояние h в сторону действия силы
Q . |
Следовательно, в положении равновесия на каток |
кроме пары сил |
Q, |
Fсц с моментом Q R будет действовать уравновешивающая пара N , Р |
|
с моментом |
|
|
|
Мс N h . |
(7.20) |

Этот момент Мс называется моментом трения качения.
|
|
|
|
h |
|
|
|
|
|
|
С |
Q |
|
С |
Q |
С |
Q |
M |
|
|
|
|
|
|
С |
||||
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
P |
|
P |
|
|
|
Fсц |
|
А |
Fсц |
А В |
|
Fсц |
А |
|
|
|
|
N |
|
|
N |
|
N |
|
|
|
|
а |
|
б |
|
в |
|
|
|
Рис 7.11
Считая деформацию малой можно заменить систему сил на рис. 7.11, б системой сил, изображенной на рис. 6.6, в, где в отличие от первой схемы
(рис. 7.11, а) к цилиндру приложен момент трения качения Мс .
Составим уравнения равновесия для цилиндра (рис. 7.11, в), находящегося под действием плоской произвольной системы сил:
Fкx 0 , |
Fку 0 , |
mА( Fк ) 0 ; |
|
|
n |
|
n |
n |
|
к 1 |
|
к 1 |
к 1 |
|
или |
|
Q Fсц 0, |
|
|
|
|
|
||
|
|
|
|
|
|
|
N P 0, |
|
|
|
|
|
0. |
|
|
|
Q R MC |
|
|
Отсюда Q Fсц , |
N P, и с учетом (7.20) |
|
|
|
|
|
MC Q R N h . |
(7.21) |
|
Из (7.21) находим |
|
|
|
|
|
|
Q R |
|
|
|
|
h N |
. |
(7.22) |
Из (7.22) видно, что с увеличением силы Q растет расстояние h,
однако оно связано с размером площадки контакта АВ, и не может неограниченно увеличиваться. Поэтому наступит такое состояние, когда
увеличение силы Q приведет к нарушению равновесия и цилиндрический
каток покатится.
Следовательно, каток находится в равновесии при

h . |
(7.23) |
Линейная величина называется коэффициентом трения качения и измеряется обычно в сантиметрах. Значение зависит от материала и определяется опытным путем. Например, = 0,05 0,08 см при качении дерева по дереву; = 0,005 см при качении мягкой стали по стали (колесо по рельсу); = 0,001 см при качении закаленной стали по стали (шаровой подшипник).
Условие равновесия (7.22) для катка можно записать в виде
MC N . |
(7.24) |
или с учетом (7.21)
Q R N .
Следовательно, при равновесии катка отсутствие скольжения и качения будет при одновременном выполнении двух условий:
|
Q fсц |
N ; |
|
Q |
|
N . |
|
(7.25) |
|
|
|
|
|||||
|
|
|
|
|
R |
|
|
|
Однако |
отношение |
/ R |
для |
большинства |
материалов меньше |
|||
коэффициента сцепления |
fcц . Поэтому по мере увеличения сдвигающей силы |
|||||||
Q сначала преодолевается второе условие (7.25), и для |
/ R Q fсц N |
|||||||
каток катится |
без скольжения. |
При |
Q fсц N |
кроме |
качения катка |
|||
происходит еще и его скольжение.
Следовательно, для большинства материалов преодолеть сопротивление качению легче, чем преодолеть сопротивление скольжению. Поэтому в технике, когда возможно, стремятся скольжение заменить качением (колеса, катки, шариковые и роликовые подшипники).
ЛЕКЦИЯ 8
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
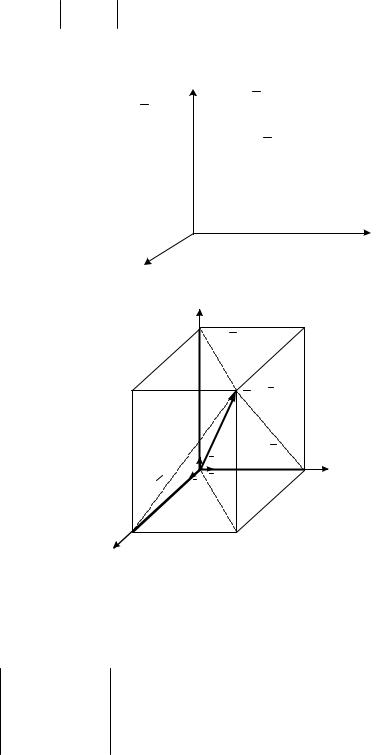
Момент силы относительно оси
Проекция момента mO (F) силы F относительно центра (точки) О, на
ось z, проходящую через этот центр, называется моментом силы F
относительно оси z, т. е.
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
(8.1) |
|
|
|
|
|
|
|
mZ (F ) mO (F ) cos γ |
|
|
|
|
|||||||
где γ |
угол между вектором mO (F) и осью z (рис. 8.1). |
|
|
|
||||||||||||||
|
|
Из (8.1) имеем, что момент силы |
|
|
|
z |
|
m ( F) |
|
|
||||||||
относительно |
оси |
z |
mZ (F ) |
является |
m ( |
|
) |
|
|
|
||||||||
F |
|
|
z |
|
|
|||||||||||||
алгебраической |
величиной, |
|
знак |
O |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
F |
|
|
||||||||||
которой определяется знаком cos γ : |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) если 0 γ 90o , то mZ (F ) 0 ; |
|
|
|
|
|
|
|
h |
A |
y |
||||||||
2) если 90o γ 180o , то mZ (F ) 0 ; |
|
|
|
|
|
|
r |
|||||||||||
|
|
x |
O |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) |
если |
90o , |
|
т. е. сила F |
|
|
|
|
Рис. 8.1 |
|
|
|||||||
коллинеарная оси z, то mZ (F ) 0 . |
|
|
|
|
|
z |
|
|
|
|
||||||||
|
|
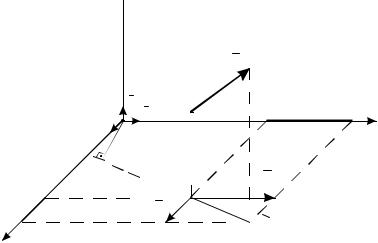
Пусть точка О начало координат |
|
|
|
m (F) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
декартовой системы. Тогда, проецируя |
|
|
|
|
z |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
вектор mO (F) |
на оси, разложим его по |
|
|
|
|
|
m (F) |
|
|
|||||||||
трем |
|
взаимно |
перпендикулярным |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
O |
|
|
||||||||||
направлениям (рис. 8.2): |
|
|
|
|
|
|
|
|
|
|
y |
|
||||||
r |
|
|
|
my (F) j mz (F) k , |
(8.5) |
|
|
|
O k |
my(F) |
|
|||||||
mO (F) mx (F) i |
|
|
) |
i |
j |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(F |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
где |
|
mx (F), |
my (F), |
mz (F) |
|
моменты |
|
m |
|
|
|
|
|
|||||
|
x |
|
|
|
|
|
|
|
||||||||||
силы |
F относительно осей Ох, Оу, |
Оz |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Рис. 8.2 |
|
|
||||||||||||
соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Для получения аналитических формул для определения моментов силы |
||||||||||||||||
относительно декартовых осей распишем формулу (6.4) в декартовой системе |
||||||||||||||||||
координат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
r |
r |
r |
r |
i |
|
j |
k |
|
|
|
|
|
|
|
|
|
|
|
x |
|
y z |
|
|
|
|
|
|
|
|
|||||
|
|
|
mO |
(F ) |
r |
F |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Fx |
Fy |
Fz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yFz zFy i zFx |
xFz j xFy |
yFx k . |
|
(8.6) |
|||||||||
Сопоставляя (8.6) с (8.5), находим аналитические формулы для вычисления |
||||||||||||||||||
моментов силы F относительно осей Ох, Оу, Оz: |
|
|
|
|
|
|||||||||||||
mx (F) yFz zFy , |
my (F) zFx xFz , |
mz (F) xFy yFx . |
|
(8.7) |
||||||||||||||
Теперь получим простое правило вычисления момента силы F относительно оси z. Для этого определим алгебраический момент Fху
проекции силы F на плоскость Оху, перпендикулярную оси z, относительно точки О, лежащей в этой плоскости (рис. 8.3).
x
Fx
x
z 
|
|
|
|
|
|
z) |
|
|
|
|
|
, |
|
|
|
|
|
|
|
y |
|
|
|
|
|
, |
|
|
|
|
|
|
x |
|
O k j |
( |
|||||
A |
||||||
|
|
|||||
|
|
|
|
|
|
|
i |
h |
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|
|
|
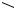
 A1
A1
F1
F
y Fy y
F2
 Fxy
Fxy
Рис. 8.3
Воспользуемся теоремой Вариньона и разложим силу Fху в точке
А1(х,у,0) на составляющие F1 иF2 , где F1 Fx |
|
и F2 Fy . Тогда согласно (6.3) |
|||||||
и (6.20) |
|
|
|
||||||
mO Fху |
|
Fху |
|
h F1 y F2 |
|
xFy yFx . |
(8.8) |
||
|
|
||||||||
Сравнивая (8.8) с (8.7), получаем |
|
|
|
||||||
mz (F ) mO Fху |
|
Fху |
|
h , |
(8.9) |
||||
|
|
||||||||
где h − плечо силы Fху относительно точки О.
Формула (8.9) дает простое правило вычисления момента силы относительно оси: для вычисления момента силы относительно оси следует спроецировать силу на плоскость, перпендикулярную оси, и затем определить алгебраический момент полученной проекции силы относительно точки пересечения данной оси с этой плоскостью.
В (8.9) mZ (F ) будет иметь знак «+», если с конца оси z сила Fху видна,
стремящейся повернуть тело вокруг оси против хода часовой стрелки, и знак « » по ходу часовой стрелки.
Момент силы относительно оси характеризует вращательный эффект силы вокруг оси.
Из (8.9) следуют два важных для практики частных случая:

1)если сила параллельна оси, то ее момент относительно оси равен нулю ( Fху 0 );
2)если линия действия силы пересекает ось, то ее момент
относительно данной оси также равен нулю (h = 0).
При вычислении момента силы относительно оси обычно пользуются
теоремой Вариньона для моментов силы относительно оси. Проецируя векторное выражение (6.20) на ось z, получим
r |
n |
r |
|
mz (R) mz (Fк) . |
(8.10) |
||
к 1
Момент равнодействующей относительно выбранной оси равен алгебраической сумме моментов составляющих сил относительно этой оси.
Вычисление главного вектора и главного момента пространственной системы сил
Главный вектор R , равный геометрической сумме сил F1, F2, , F3, ...,
Fn , в декартовых координатах определяется по модулю и направлению применением полученных выше формул (5.8) – (5.11).
Для вычисления главного момента MO системы сил F1, F2, , F3, ..., Fn относительно центра (точки) О:
r |
n |
r |
r |
n |
r r |
, |
(8.11) |
МО mО (Fк ) rк Fк |
|||||||
|
к 1 |
|
|
к 1 |
|
|
|
следует начало декартовой системы координат Охуz поместить в центре О, и затем разложить вектор MO по трем взаимно перпендикулярным направлениям аналогично (8.5):
MO (F ) Mx i M y j Mz |
k . |
(8.12) |
Здесь Mx , M y , Mz − главные моменты системы |
сил |
F1, F2, , F3, ..., Fn |
относительно осей Ох, Оу, Оz соответственно, определяются как проекции главного момента MO на эти координатные оси:
n |
r |
n |
r |
n |
r |
|
Mx mx (Fк ), |
My my (Fк ), |
Mz mz (Fк ). |
(8.13) |
|||
к 1 |
|
к 1 |
|
к 1 |
|
|

Модуль и направление главного момента вычисляются по формулам:
|
|
|
|
|
|
MO |
Mx |
2 |
M y |
2 |
Mz |
2 , |
|
|
|
|
(8.14) |
|
|
r r |
|
M |
|
|
r r |
|
M y |
|
|
|
r r |
|
M |
z |
|
||
cos MO i |
|
|
x |
, |
cos MO j |
|
|
|
, cos MO k |
|
|
. (8.15) |
||||||
|
MO |
|
MO |
|||||||||||||||
|
|
|
MO |
|
|
|
|
|
|
|
|
|
|
|||||
Частные случаи приведения пространственной системы сил
Согласно теореме Пуансо любую систему сил, действующую на
|
|
|
|
|
|
|
|
|
|
n |
абсолютно |
твердое тело, можно заменить |
главным |
вектором |
R |
Fк , |
|||||
|
|
|
|
|
|
|
|
|
|
к 1 |
приложенным в |
центре |
приведения, |
и |
парой |
сил |
с |
моментом |
|||
|
n |
|
равным |
главному моменту |
системы сил |
относительно |
||||
МО mО (Fк ) , |
||||||||||
к 1
центра приведения.
Рассмотрим частные случаи приведения системы сил к произвольному центру О.
1) R 0, МО 0.
Если главный вектор системы сил не равен нулю, а её главный момент относительно этого центра равен нулю, то система сил приводится к
равнодействующей R равной главному вектору, линия действия которой проходит через центр приведения О.
2) R 0, МО 0.
Если главный вектор системы сил равен нулю, а ее главный момент относительно центра приведения О не равен гулю, то система сил
приводится к паре с моментом равным главному моменту МО системы сил
относительно центра приведения О. Поскольку момент пары вектор свободный, то в этом случае главные моменты системы сил относительно любых центров приведения геометрически равны.
3) R 0, МО 0, |
МО R (рис. 8.4, а). |
|
|
Представим главный вектор МО парой сил |
R , R , |
лежащей в |
|
перпендикулярной ему плоскости, такой, что R R, |
R R , |
а плечо пары |
|
d МО / R (рис. 8.4, б). |
|
|
|
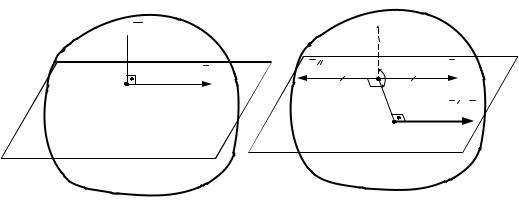
Так как силы R и R образуют уравновешенную систему сил, то согласно аксиоме 2 она может быть отброшена. Тогда получаем, что
исходная система сил приводится к равнодействующей R R , линия действия которой проходит через точку О1, находящуюся в
перпендикулярной вектору МО плоскости и отстоящую от центра приведения О на расстоянии ОО1 d МО / R .
 MО
MО
O |
R |
90 О |
а |
б |
|
Рис. 8.4 |
Так как силы R |
и R образуют уравновешенную систему сил, то |
согласно аксиоме 2 она может быть отброшена. Тогда получаем, что
исходная система сил приводится к равнодействующей R R , линия действия которой проходит через точку О1, находящуюся в
перпендикулярной |
вектору |
МО плоскости и |
отстоящую |
от центра |
|
приведения О на расстоянии ОО1 d МО / R . |
|
|
|||
4) R 0, МО 0, |
МО R (рис. 8.5, а). |
|
|
||
Представим |
главный |
вектор МО парой |
сил F, F , |
лежащей в |
|
перпендикулярной ему плоскости (рис. 8.5, б).
Совокупность главного вектора R и пары сил F, F с моментом
МО , лежащей в плоскости перпендикулярной линии действия силы R , называется силовым винтом, или динамой. Прямая, по которой направлены векторы R и МО , называется осью динамы.
Следует отметить, что динама не допускает дальнейшего упрощения. Действительно, сложив в точке О силы R и F , найдем вектор Q R F ,
который лежит в плоскости перпендикулярной силе F . Поскольку силы Q и F направлены по скрещивающимся прямым, то их нельзя сложить (рис. 8.5, в).
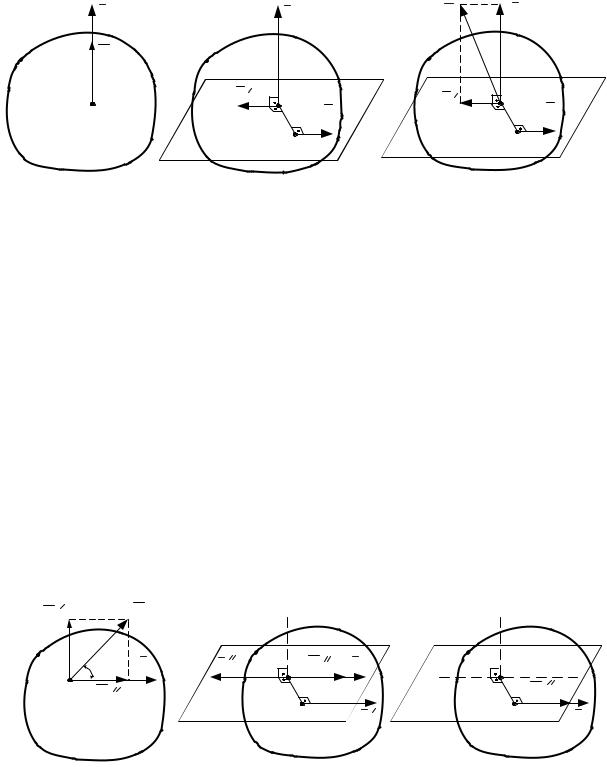
R |
R |
|
Q |
R |
MО |
|
|
|
|
O |
F O |
F |
F |
F |
|
|
|
|
а |
|
|
б |
в |
|
|
|
|
|
|
Рис. 8.5 |
|
|
|
|
r |
r |
|
r r |
|
|
|
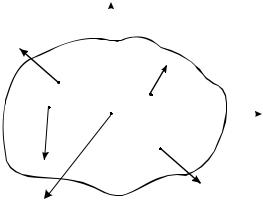
5) |
R 0, |
МО 0, |
(МО, R) (см. рис. 8.6, а). |
|
|
||
Разложим главный момент МО в точке О на два вектора МО и |
МО |
||||||
( МО MO MO ), где МО |
перпендикулярен главному векторуR , |
а МО напра- |
|||||
влен по нему (рис. 8.6, |
а). Определим модули этих векторов: |
МО MO sin , |
|||||
МО MO cos . |
|
|
|
|
|
|
|
Согласно |
частному случаю 3) представим |
вектор МО парой |
сил |
||||
R , R , |
лежащей |
в |
перпендикулярной ему |
плоскости, |
такой, |
что |
|
R R, |
R R , |
а плечо этой пары d МО / R (рис. 8.6, б). В точке О |
|||||
силы R |
и R образуют уравновешенную систему сил, которая может быть |
||||||
отброшена.
MО |
|
MО |
|
|
|
|
O |
|
R |
R O MО |
R |
O |
|
MО |
|
d |
|
d |
MО |
|
|
|
|
||||
|
|
O1 |
R |
O1 |
||
|
|
|
R |
а |
б |
в |
|
Рис 8.6 |
|
Поскольку момент МО |
пары сил есть вектор свободный, то его можно |
|
из центра О перенести в центр О1.
Тогда получаем, что исходная система сил приводится к главному вектору R R , линия действия которого проходит через точку О1, и к паре
сил |
с моментом МО параллельным вектору R . Согласно случаю 4) такая |
система сил приводится к динаме, ось которой проходит через точку О1 на
расстоянии ОО1 d |
|
МО sin |
от центра приведения О (рис. 8.6, в). |
|
|
R |
|
6). R 0, МО 0.
В этом случае на абсолютно твердое тело действует уравновешенная система сил. Следовательно, тело будет находиться в равновесии.
Уравнения равновесия для пространственной системы сил
В (7.17) было установлено, что для равновесия твердого тела, находящегося под действием произвольной системы сил, необходимо и достаточно, чтобы главный вектор и главный момент относительно любого центра для этой системы сил были равны нулю:
R 0, |
МО 0 . |
(8.16) |
Найдем вытекающие из (8.16) аналитические условия равновесия для пространственной системы сил.
1. Произвольная пространственная система сил. Пусть абсолютное твердое тело находится в равновесии под действием произвольной пространственной системы сил (рис. 8.7). Условия (8.16) означают, что при
равновесии проекции векторов R и МО на оси декартовой системы координат Охуz должны быть равны нулю, т. е.
Rх 0, |
Ry 0, |
Rz 0, |
(8.17) |
|
Mx 0, |
M y 0, |
Mz 0. |
||
|
С учетом (5.8) и (8.13) уравнения (8.17) запишем в виде шести скалярных уравнений равновесия:
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
n |
|
n |
r |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1) Fкx |
0; |
4) mx (Fк ) 0; |
|
||
Fn |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
к 1 |
|
к 1 |
|
|
|||||
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
r |
|
||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
O |
|
|
|
|
|
|
|
y |
2) |
Fкy = 0; |
5) my (Fк ) 0; |
( 8.18) |
||
|
|
|
|
|
|
|
|
|
|
|
|
к 1 |
|
к 1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
r |
|
|
|
|
|
|
|
|
|
|
|
|
3) Fкz |
0; |
6) mz (Fк ) 0. |
|
||||
|
F3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к 1 |
|
к 1 |
|
|
|
|
x |
|
|
|
F2 |
|
Уравнения |
(8.18) |
называются |
||||||||
|
|
|
|
Рис. 8.7 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
