
u_lectures
.pdfвращательном движении тела радиус-вектор |
|
r |
|
точки, изменяя своё |
направление, остаётся постоянным по модулю |
|
r |
|
ОМ const . Тогда из |
|
|
(2.18) получим выражение для полной производной по времени от вектора r
изменяющегося по направлению с угловой скоростью , но постоянного по модулю:
|
dr |
|
r |
r |
|
(2.19) |
|
|
dt |
ω r. |
|
||||
|
|
|
|
|
|
||
Для определения ускорения точки М продифференцируем по времени |
|||||||
равенство (2.18): |
|
|
|
|
|
|
|
dV |
|
|
r |
r |
r |
r |
|
|
dω |
dr |
. |
||||
dt |
|
dt |
r |
ω |
dt |
||
|
|
|
|
|
|||
Отсюда находим выражение полного ускорения точки вращающегося тела
r r
a ε r ω V ,
где касательное и нормальное ускорения соответственно равны
ar εr r r, an ω V.
Действительно, модули этих векторов одинаковы:
(2.20)
(2.21)
|
r |
r |
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
r |
r |
|
ε R |
|
r |
|
; |
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
ε r |
|
|
ε |
|
|
|
r |
|
|
sin ε, r |
|
aτ |
|
|||||||||||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
r |
|
|
|
π |
|
2 |
R |
|
r |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin |
ω |
|
|
. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
ω V |
|
|
|
ω |
|
|
V |
|
2 |
|
|
an |
|
|
|||||||||||||||||||
Вектор ε r направлен так же, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
как вектор aτ , по касательной к траектории |
|||||||||||||||||||||||||||||||||||
точки М, а вектор ω V |
|
так же, как вектор нормального ускорения an , по |
|||||||||||||||||||||||||||||||||
радиусу МС к оси вращения (см. рис 2.7). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ЛЕКЦИЯ 3
ПЛОСКОПАРАЛЛЕЛЬНОЕ (ПЛОСКОЕ) ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

Плоскопараллельным (плоским) называется движение твердого тела, все точки которого движутся в плоскостях, параллельных неподвижной
плоскости. |
|
|
|
|
|
у |
|
|
|
Охz |
Качение цилиндра по плоскости |
M |
|
||||||
является |
плоскопараллельным |
|
|
||||||
|
|
|
|||||||
движением, если плоскости его |
|
|
|
||||||
оснований |
S |
и |
S1 |
остаются |
|
S |
х |
||
параллельными |
|
неподвижной |
О |
|
|||||
плоскости Оху (рис. 3.1). При этом |
|
|
|
||||||
любая образующая ММ1 |
цилиндра |
M1 |
|
|
|||||
совершает |
поступательное |
движение, |
|
|
|||||
|
|
|
|||||||
то |
есть |
|
кинематические |
S1 |
|
|
|||
характеристики |
ее |
|
точек |
в z |
|
|
|||
произвольный |
момент |
времени |
|
|
|
||||
одинаковы: |
VM VM1 , |
aM aM1 и точки |
|
Рис. 3.1 |
|
||||
М и М1 описывают тождественные траектории.
Следовательно, изучение плоскопараллельного движения твердого тела сводится к изучению движения плоского сечения S в его плоскости.
Положение плоского сечения S в плоскости Оху (рис. 3.2) определяется положением любого отрезка АМ, проведенного в этом сечении. Для этого необходимо задать координаты хА, уА какой-нибудь точки А, называемой полюсом, и угол , который отрезок АМ образует с осью Ох.
При движении плоской фигуры (сечения S) координаты хА, уА и угол φ будут изменяться во времени:
xA f1 t , |
yA f2 t , |
f3 t . |
|
|
|
|
(3.1) |
Зависимости |
(3.1) |
называются |
|
уравнениями плоскопараллельного движения твердого тела.
Из (3.1) видно, что изменение только координат хА и уА приводит к
поступательному |
движению |
плоской |
фигуры вместе |
с полюсом А, а |
|
изменение только |
угла φ |
к |
вращательному движению плоской фигуры
вокруг оси, проходящей через |
полюс А |
и перпендикулярной плоскости |
движения |
Оху. |
|
у
(S) М
уА А
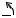

О |
хА |
х |
Рис. 3.2
Следовательно, движение плоской фигуры (сечения S) в ее плоскости можно представить как совокупность поступательного движения вместе с полюсом и вращательного движения вокруг этого полюса. Подчеркнем, что

угловая скорость ω и угловое ускорение ε при плоскопараллельном движении тела от выбора полюса не зависят.
По заданным уравнениям плоского движения тела (3.1) можно найти скорость и ускорение полюса А, а также угловую скорость и угловое ускорение тела по формулам:
r |
|
r |
|
r |
V |
A |
x&i |
y& j; |
|
|
A |
A |
|
|
r |
|
r |
&y |
r |
a |
A |
&x i |
j; |
|
|
A |
A |
|
|
d &; dt
|
A |
|
|
A |
2 |
|
|
A |
|
2 ; |
|
V |
|
|
|
x& |
|
|
y& |
|
|
||
|
A |
|
A |
2 |
|
A |
2 ; |
|
|||
a |
|
|
|
&x |
|
|
&y |
|
(3.2) |
d &. dt
Угловая скорость ω и угловое ускорение ε изображаются дуговыми стрелками
(рис. 3.3).
Скорости точек плоской фигуры
Скорость любой точки тела, совершающего плоскопараллельное движение, определяется по теореме о скоростях точек плоской фигуры:
скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и скорости точки во вращательном движении вокруг полюса.
Доказательство. Пусть в произвольный момент времени t скорость точки А плоской фигуры равна VA , а угловая скорость фигуры ω (рис. 3.3). Приняв точку А за полюс, найдем скорость любой точки М фигуры. Проведем из неподвижной точки О в точки А и М радиус-векторы rA , rM и соединим эти
точки вектором АМ постоянным по модулю ( АМ const , так как тело
абсолютно твердое). Положения точек А и М в любой момент времени t связаны равенством
|
r |
r |
|
(3.3) |
|||
|
rМ |
rA AМ . |
|
||||
у |
VA |
Вычислив |
от обеих частей |
||||
VМ |
равенства |
(3.3) |
производную по |
||||
(S) |
времени, получим |
||||||
|
|||||||
|
М |
r |
r |
|
d AM |
|
|
VМ,А |
VA |
drM |
drA |
|
|||
dt |
|||||||
rМ |
|
dt |
dt |
|
|||
А |
|
|
|
|
|
||
rA |
или с учетом (1.2) и (2.18), находим |
||||||
О  х
х
Рис. 3.3
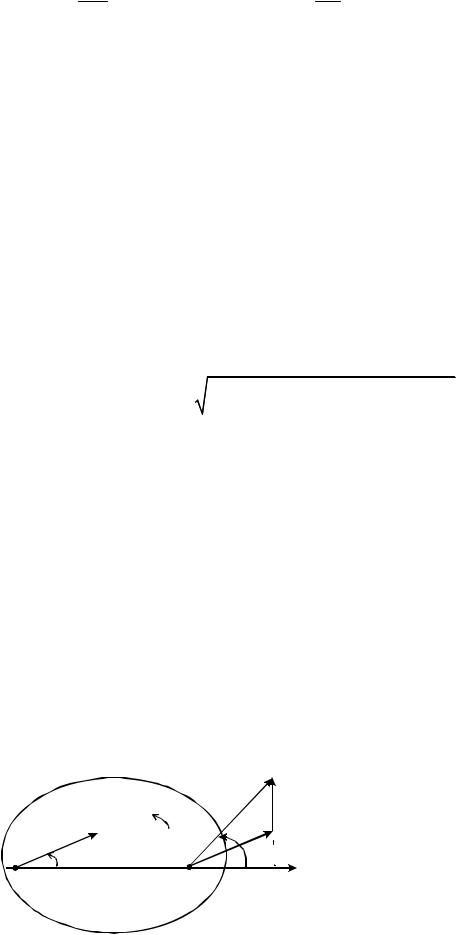
VМ VA V МA . |
(3.4) |
Здесь VМ ddtrM скорость точки М, VA ddtrA скорость точки А, а вектор
r |
(3.5) |
V MА ω AM |
вращательная скорость точки М вокруг полюса А. Вектор V MА по модулю равен
|
|
VMA ω AM |
(3.6) |
и изображается на рис. |
3.3 в точке М перпендикулярно АМ (V AM АМ ) |
||
в направлении вращения плоской фигуры (в направлении ω). |
|
||
Вектор скорости |
VМ |
точки М определяется |
диагональю |
параллелограмма, построенного на векторах VA и V MА как на сторонах (рис. 3.3), и его модуль равен
VM VA2 VMA2 |
|
r |
r |
|
2VAVMA cos(VA |
VMA ) . |
(3.7) |
||
Когда уравнения (3.1) неизвестны, из формулы (3.4) определяют угло- |
||||
вую скорость плоской фигуры по известным величинам скорости |
V MА и |
|||
расстояния АМ. |
|
|
|
|
ω |
VMA |
|
|
(3.8) |
AM |
|
|||
|
|
|
||
Теорема о проекциях скоростей двух точек плоской фигуры
Соотношение между величинами скоростей точек А и М плоской фигуры можно найти более простым способом по теореме о проекциях скоростей двух точек фигуры: проекции скоростей двух точек плоской фигуры на ось, проходящую через эти точки, равны.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
Спроецируем |
|
|
|
|
|
|
|
|
|
VМ |
векторное равенство (3.4) на ось |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ах, проходящую через точки А |
|
|
|
|
|
|
|
|
|
|
|
|
|
VМ,А |
|||||
|
|
|
|
|
|
|
|
|
|
|
и М (рис. 3.4). |
Учитывая, что |
|||||
|
|
|
|
VA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VA |
вектор VMA перпендикулярен |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
АМ, получим |
|
|
А |
VAx |
|
|
М |
VMx х |
|
|||||||||||
|
|
|
|
||||||||||||||
(S)
Рис. 3.4
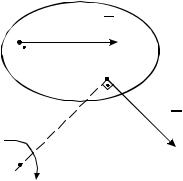
VMх VAх
или
VM cosβ VA cosα. |
(3.9) |
Теорема (3.9) позволяет находить скорость любой точки М плоской фигуры, если известно ее направление и скорость другой точки А по модулю и направлению. Теорема (3.9) имеет место для любого движения абсолютно твердого тела.
Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется точка Р плоской фигуры, скорость которой в данный момент времени равна нулю (VP 0 ).
Пусть известны скорости двух любых точек А и В плоской фигуры по направлению (рис. 3.5). Докажем, что МЦС находится в точке пересечения
перпендикуляров, восстановленных в этих точках к их скоростям VA и VB . Доказательство. Пусть VP 0 , тогда по теореме (3.9) проекция
вектора VP на прямую АР равна нулю, |
и VP |
AP . Но по той же теореме |
||||||||
проекция вектора VP |
на прямую ВР также равна нулю и VP ВP . Поэтому |
|||||||||
вектор VP одновременно должен |
быть перпендикулярным |
двум |
||||||||
непараллельным |
прямым АР и ВР, что невозможно. Следовательно, |
|||||||||
допущение, что скорость точки Р не равна нулю неверно (VP 0 ). |
|
|||||||||
|
|
|
|
|
|
Примем МЦС, т. е. точку Р за полюс. |
||||
|
|
|
|
VА |
|
Тогда по теореме о скоростях (3.4) для любых |
||||
A |
|
|
|
|
точек А и В плоской фигуры S имеем: |
|
||||
|
|
(S) |
B |
|
|
|||||
|
|
|
|
|||||||
|
|
|
|
VA VP VAP |
VAP ; |
VA AP; |
|
|||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
r r |
r |
r |
r |
(3.10) |
|
|
|
|
|
|
|||||
|
|
|
|
|
V |
VB VP VBP |
VBP ; |
VB BP. |
||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
В |
|
|
|
|
|
P |
|
|
|
|
|
Следовательно, скорость любой точки |
||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
Рис. 3.5 |
|
|
тела, лежащей в сечении S, равна |
||||
|
|
|
|
|
|
вращательной |
скорости |
точки |
вокруг |
|
мгновенного центра скоростей Р. МЦС является центром вращения плоской
фигуры |
(сечения S) в данный момент времени и находится в точке |
пересечения |
перпендикуляров АР и ВР, восстановленных в точках А и В |
к их скоростям VA и VB .

Согласно (3.10) и с учетом (3.6) модули скоростей точек определяются по формулам:
VA ω AP; |
(3.11) |
||
VB |
ω BP. |
||
|
|||
Из равенства (3.11) следует пропорция |
|
||
VA |
AP . |
(3.12) |
|
VB |
BP |
|
|
Скорости точек плоской фигуры пропорциональны их расстояниям до мгновенного центра скоростей.
Соотношение (3.11) позволяет определить угловую скорость тела при плоском движении
ω |
|
VA |
. |
(3.13) |
|
||||
|
|
AP |
|
|
Угловая скорость плоской фигуры в каждый момент времени равна отношению скорости любой точки плоской фигуры к её расстоянию до мгновенного центра скоростей.
Для применения формул (3.9) и (3.10) при решении задач необходимо уметь определять положение мгновенного центра скоростей в данный момент времени.
Кроме способа нахождения МСЦ, представленного на рис. 3.5,
рассмотрим еще некоторые частные случаи: |
|
|
|
|
|
|
|
|
|
||||||
1. Если известны скорости |
|
|
|
|
VА |
|
A |
|
|
VА |
|||||
VA и VB двух точек |
А и |
В |
A |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
плоской |
фигуры параллельные |
(S) |
|
|
|
|
|
(S) |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||
между |
собой |
|
и |
B |
|
VВ |
|
P |
|
|
|
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
перпендикулярные прямой АВ, |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
то МЦС |
находится |
в точке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
пересечения прямой |
АВ |
с |
P |
|
|
|
|
|
|
|
|
B |
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
прямой, |
соединяющей |
концы |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
VВ |
|
|
|
||||||
векторов |
скоростей |
точек |
|
|
|
|
|
|
|
|
|
||||
(рис. 3.6). |
|
|
|
|
|
а |
|
Рис. 3.6 |
|
б |
|
||||
2. Если скорости VA и VB |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
двух точек А и В плоской фигуры параллельные между собой и не перпендикулярные прямой АВ (рис. 3.7, а), или скорости двух точек фигуры параллельные, равные и перпендикулярные отрезку АВ (рис. 3.7, б), то МЦС находится в бесконечности. Угловая скорость плоской фигуры в данный момент времени равна нулю: ω 0 и тело имеет мгновенно поступательное

распределение скоростей, т. е. в данный момент времени скорости всех точек
плоской фигуры геометрически равны: |
VA = VB . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
(S) |
|
|
|
A |
|
|
|
VА |
A |
|
|
|
|
VА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
VВ |
|
|
|
|
(S) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
б |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.7 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. При качении одного цилиндрического |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
тела по поверхности другого неподвижного тела |
|||||||||||
VA |
|
|
|
A ( |
|
|
|
|
|
|||||||||||||||
|
|
|
) |
|
|
(рис. |
3.8) точка касания Р катящегося тела о |
|||||||||||||||||
|
|
|
|
|
|
|
S |
|
|
|
|
|
неподвижную поверхность имеет в данный |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
момент времени скорость равную нулю (VP 0 ) и |
|||||||||||
|
|
|
|
|
|
P |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
является мгновенным центром скоростей. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Рис. 3.8 |
|
|
|
|
|
|
|
4. Если известен вектор скорости VA точки А |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
плоской фигуры и ее угловая скорость ω, то для |
|||||||||||
|
|
|
|
|
|
|
VА |
|
|
|
|
|
определения МЦС точки Р следует вектор VA |
|||||||||||
|
|
A |
|
|
|
|
|
|
|
|
повернуть вокруг точки А на 90 в направлении ω |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
(S) |
и на |
этой |
полуоси отложить расстояние АР |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
(рис. 3.9), которое определяется согласно (3.13) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
P |
|
Рис. 3.9 |
|
|
|
|
|
равенством |
|
|
|
АР |
VA |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|||
Ускорения точек плоской фигуры
Ускорение любой точки тела, совершающего плоскопараллельное движение, определяется по теореме об ускорениях точек плоской фигуры:
ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения точки во вращении вокруг полюса.

у
а ,А М
О
Доказательство. Пустьв произвольный момент времени t ускорение точки А плоской
М |
|
|
фигуры равно аA , |
угловая скорость фигуры |
|
|
|
|
|
ω, а угловое ускорение ε (рис. 3.10). |
|
|
а |
n |
|
Примем точку А за полюс и найдем |
|
|
,А |
|
ускорение любой точки М фигуры. |
||
|
|
|
|||
(S) |
М |
а |
|
|
|
А |
|
Согласно теореме о скоростях (3.4) |
|||
|
|
A |
|||
|
|
|
х |
VМ VA V MA |
|
Рис. 3.10 |
|
или с учетом (3.5) |
|
||
|
|
|
|
|
|
|
|
|
|
r |
(3.14) |
|
|
|
VМ VA ω АМ . |
||
Вычислив производные по времени от левой и правой частей равенства
(3.14), получим
|
|
r |
|
r |
|
r |
uuuur |
r |
d AM |
|
|
||
|
|
dV |
|
dV |
|
|
dω |
|
|
||||
|
|
M |
|
A |
|
АМ |
ω |
|
. |
(3.15) |
|||
|
|
|
dt |
dt |
|||||||||
|
|
dt |
|
dt |
|
|
|
|
|
|
|||
|
dV |
|
dVA |
|
|
|
|
|
|
|
|
|
|
Здесь |
M |
aМ ; |
|
aA |
ускорения точек М и А соответственно; |
|
|||||||
dt |
|
||||||||||||
dt |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
dω |
|
uuuur |
r |
uuuur |
r τ |
|
(3.16) |
|
|
|
|
|
|
dt |
|
АМ |
ε АМ аМА |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
согласно (2.21) касательное ускорение точки М во вращение вокруг полюса
А;
r |
d AM |
r |
r r n |
|
ω |
|
ω VMA aMA |
||
dt |
||||
|
|
|
||
нормальное ускорение точки М во вращение вокруг полюса А. Тогда (3.15) принимает вид
аМ аА аМАn аМАτ
или
аМ аА аМА ,
где аМА полное ускорение точки М во вращении вокруг полюса А:
(3.17)
(3.18)
(3.19)

аМА аМАn |
аМАτ |
. |
(3.20) |
у |
|
|
|
|
|
|
|
|
|
|
|
Модули аМАn |
и |
аМАτ |
вычисляются по |
М |
а |
|
|
формулам: |
|
|
|
|
|
A |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
аМАn ω2 АМ ; |
(3.21) |
аМАτ ε АМ . |
(3.22) |
(S)
аМ 
О
А |
а ,А |
n |
|
М |
|
|
|
а |
|
,А |
|
М |
х |
|
Вектор аМАn |
проведем из М к полюсу А |
Рис. 3.11 |
||
по АМ, а вектор |
аМАτ |
приложим в точке М и |
||
|
||||
направим перпендикулярно аМАn в направлении ε, (рис. 3.10).
На рис. 3.11 вектор полного ускорения аМ точки М определяется построением многоугольника ускорений (3.18): начало вектора аМ совпадает с началом вектора ускорения полюса аА , а его конец с концом вектора
аМАτ .
ЛЕКЦИЯ 4
СЛОЖНОЕ (СОСТАВНОЕ) ДВИЖЕНИЕ ТОЧКИ Теорема о сложении скоростей
Сложное (составное) движение точки это такое движение, при котором она одновременно участвует в двух или более движениях.
|
z |
|
Для характеристики сложного |
||||||
Z |
|
движения |
точки |
введем |
две |
||||
|
|
||||||||
|
|
|
системы |
отсчета: |
ОХYZ |
|
|||
|
M |
|
неподвижную |
и |
Ахуz |
|
|||
|
|
подвижную, |
связанную |
|
|
с |
|||
|
D |
у |
движущимся |
телом |
|
D, |
|||
|
|
относительно |
|
|
которого |
||||
|
|
|
|
|
|||||
|
A |
|
перемещается точка М (рис. 4.1). |
||||||
|
|
Y |
Движение |
точки |
М |
по |
|||
O |
х |
отношению |
к подвижной |
системе |
|||||
|
|||||||||
|
|
|
отсчета |
Ахуz |
|
называется |
|||
Х |
|
|
относительным |
|
движением. |
||||
|
|
Скорость и |
ускорение точки М в |
||||||
Рис. 4.1 |
|
|
|||||||
|
|
|
|
|
|
|
|
||

этом движении называются относительной скоростью Vr и относительным
ускорением ar .
Движение тела D и связанного с ним подвижного трехгранника Ахуz относительно неподвижного трехгранника ОХYZ называется переносным движением. Скорость и ускорение точки подвижного тела D, с которой в данный момент времени совпадает точка М, являются для нее переносной
скоростью Vе и переносным ускорением aе .
Движение точки М относительно неподвижной системы координат ОХYZ называется абсолютным движением. Скорость и ускорение точки М относительно неподвижного трехгранника ОХYZ называются абсолютной
скоростью Vа и абсолютным ускорением aа .
Основная задача сложного движения точки заключается в установлении связей между основными кинематическими характеристиками относительного, переносного и абсолютного движений точки.
Связь между относительной, переносной и абсолютной скоростями точки выражается теоремой о сложении скоростей: абсолютная скорость точки при сложном движении равна геометрической сумме переносной и относительной скоростей.
Доказательство. Пусть скорость точки А тела D равна VA , а его угловая скорость в данный момент времени ωe . Найдем абсолютную
скорость Va точки М, движущейся относительно тела D. Положения точек А и М относительно неподвижной системы отсчета ОХУZ определяются радиус-векторами rA и rМ соответственно. Положение точки М относительно подвижной системы отсчета Ахуz (тела D) задано радиус-
вектором ρr АМ (рис. 4.2). В каждый момент движения положения точек А и М связаны равенством
rM rA . |
(4.1) |
Здесь |
|
|
|
yj zk , |
(4.2) |
|
xi |
||
где i , |
j , k – |
орты подвижной |
|
системы Ахуz, а х, у, z – координаты |
|||
точки М |
в этой системе отсчета. |
||
Дифференцируя (4.1) по времени, |
|
получим |
Х |
|
Z |
z |
|
|
|
|
|
|
|
rM |
M |
|
|
|
|
|
|
|
|
D |
|
|
|
у |
|
A |
|
|
O |
rA |
х |
Y |
|
|
drM |
|
drA |
|
d |
Рис. 4.2 |
|
|||||
|
|
dt . |
(4.3) |
||
dt |
dt |
