
u_lectures
.pdfвращению, т. е. Mz и d направлены в противоположные стороны. Полная работа силы при повороте тела на угол 1 определяется выражением
|
|
|
A 1 |
Mzd . |
(17.15) |
0 |
|
|
Если момент силы относительно оси вращения является постоянной величиной Mz const , то работа определяется по формуле
|
A Mz |
1. |
(17.16) |
Вычислим теперь мощность силы, вращающей тело вокруг |
|||
неподвижной оси. С учетом (12.14) получим |
|
|
|
N dA |
Mz d Mzω. |
|
|
dt |
dt |
|
|
Следовательно, при действии силы на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела.
6. Работа системы сил. Если на материальную точку В действует система сил F1, F2 , ..., Fn , то полная работа определяется как алгебраическая сумма работ каждой из сил в отдельности:
n |
n |
B1 |
Fкxdx Fкydy Fкzdz . |
|
А Aк |
|
(17.17) |
||
к 1 |
к 1 |
B |
|
|
|
|
0 |
|
|
7. Потенциальные силы. В общем случае при вычислении работы силы по формуле (17.17) необходимо в интеграле перейти к одному переменному, т. е. знать зависимости y f1(x) и z f2 (x) , определяющие
уравнение траектории точки, которая обычно неизвестна. Однако существуют силы, называемые потенциальными, работа которых не зависит от вида траектории движения точки.
Для таких сил введем следующие определения. Силовым полем называется часть пространства, в каждой точке которого на материальную частицу действует определенная сила, зависящая от её положения (координат).
Силовое поле называется потенциальным, если существует функция
П(r,t) такая, что действующая |
сила F определяется по |
формуле |
|
r |
П(r,t) |
называется потенциальной |
энергией |
F П/ r , где функция |
|||
материальной точки, а сила F потенциальной силой.
Проекции потенциальной силы на декартовые оси равны взятым с обратным знаком частным производным от потенциальной энергии по соответствующим координатам:
F |
|
П |
; |
F |
|
П |
; |
F |
|
П |
. |
(17.18) |
|
|
|
||||||||||
x |
x |
|
y |
y |
|
z |
|
z |
||||
|
|
|
|
|
|
|
|
|
||||
Потенциальное поле может быть нестационарным или стационарным вследствие от того, зависит ли функция П явно от времени t или нет. Для стационарного потенциального поля, подставляя (17.18) в (17.4), находим
dA F dx F dy F dz |
|
|
|||
|
x |
y |
z |
|
|
|
П dx |
П dy |
П dz dП(x, y,z) . |
|
|
|
x |
|
y |
z |
|
Следовательно, |
|
|
|
|
|
|
|
dA dП. |
(17.19) |
||
В стационарном потенциальном силовом поле элементарная работа силы равна взятому с противоположным знаком полному дифференциалу от потенциальной энергии материальной точки.
Полная работа потенциальной силы F на перемещении материальной точки из положения В0(х0,у0,z0) в положение В1(х1,у1,z1)
|
B1 |
B1 |
|
|
АB0B1 |
|
dA |
dП П0 П1 , |
(17.20) |
|
B0 |
B0 |
|
|
где П0(х0, у0, z0), и П1(х1, у1, z1) значения потенциальной энергии П частицы в начальном В и конечном В1 положениях соответственно.
Работа потенциальной силы равна разности значений потенциальной энергии материальной точки в начальном и конечном ее положениях и от вида траектории движения не зависит.
Из (17.20) следует, что работа потенциальной силы по любому замкнутому контуру равна нулю, так как в этом случае значения потенциальной энергии в начальном и конечном положениях будут одинаковыми. Потенциальными силами являются силы тяжести, упругости, тяготения.
Из (17.19) следует, что функция П определена с точностью до аддитивной постоянной, т. е.
П dA C , |
(17.21) |
где С произвольная постоянная. Это свойство позволяет выбрать нулевую точку 0, для которой П0 0 , исходя из удобства решения конкретной задачи. Тогда из (17.20) с учетом (17.21) имеем
АBO O dA |
O dП П П0 П . |
(17.22) |
B |
B |
|
Следовательно, потенциальная энергия П материальной точки в положении В(х, у, z) равна работе, которую произведут силы поля при ее перемещении из положения В в нулевое.
Воспользовавшись (17.22) из (17.10) и (17.11) запишем выражения потенциальной энергии:
1)для поля силы тяжести (ось Оz направлена вертикально вверх, нулевая точка П (z 0) 0 ) П P z ;
2)для поля силы упругости (ось Ох проведена из конца ненапряженной пружины П (х 0) 0 ) П сх2 / 2 .
ЛЕКЦИЯ 18
Кинетическая энергия материальной точки и механической системы
Основной динамической характеристикой материальной точки и механической системы является их кинетическая энергия, как мера механического движения, приводящая к преобразованию механической энергии в другие виды энергий (потенциальную, тепловую, и т. д.).
Кинетическая энергия материальной точки равна половине произведения массы точки на квадрат ее скорости:
T |
mV 2 |
|
2 . |
(18.1) |
В системе СИ кинетическая энергия измеряется в Дж: 1 Дж = 1 кг м2/с2.
Кинетическая энергия механической системы равна сумме кинетических энергий всех материальных точек системы:
n |
1 |
n |
|
|
T Tк |
mкVк |
2 . |
(18.2) |
|
к 1 |
2 |
к 1 |
|
|
Кинетическая энергия положительна, за исключением случая, когда скорости всех точек системы равны нулю.

При вычислении кинетической энергии часто пользуются теоремой Кёнига: кинетическая энергия системы в абсолютном движении равна сумме кинетической энергии, которую имела бы материальная точка расположенная в центре масс системы и имеющая массу, равную массе системы, и кинетической энергии движения системы относительно центра масс:
|
M V 2 |
|
1 |
n |
2 |
|
|
Т |
C |
|
|
mкVкr |
(18.3) |
||
2 |
2 |
||||||
|
|
к 1 |
|
|
|||
где VC скорость центра масс системы, |
Vкr |
относительная скорость к-й |
|||||
материальной точки по отношению к центру масс С системы.
Вычислим кинетическую энергию твердого тела при различных видах его движения.
При поступательном движении твердого тела все его точки движутся с одинаковыми скоростями, равными скорости центра масс: Vк VC . Поэтому
из (18.2) получаем
Tпост |
1 |
|
n |
|
VС |
2 |
M V 2 |
(18.4) |
2 |
|
mк |
C . |
|||||
|
|
к 1 |
|
|
|
2 |
|
|
Следовательно, кинетическая энергия твердого тела при поступательном движении равна половине произведения массы тела на квадрат скорости его центра масс.
При вращении тела вокруг неподвижной оси Oz (рис. 18.1) скорость любой его к-й точки Vк ω hкz , где ω угловая скорость тела, hкz
кратчайшее расстояние от точки до оси вращения Oz. С учетом этого формула (18.2) принимает вид
|
|
T |
|
1 |
|
n |
m h 2 |
|
ω2 |
|
I |
|
ω2 |
|
||||
|
|
|
|
|
|
|
z |
|
, |
(18.5) |
||||||||
|
|
вр |
|
2 |
|
к |
кz |
|
|
|
|
2 |
||||||
|
|
|
|
|
к 1 |
|
|
|
|
|
|
|
|
|
|
|||
|
где согласно (15.1) |
|
Iz |
момент инерции тела |
||||||||||||||
|
относительно оси Оz. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
к |
Следовательно, |
|
кинетическая |
|
энергия |
||||||||||||
к |
|
|
|
|||||||||||||||
тела при вращательном движении вокруг |
||||||||||||||||||
|
||||||||||||||||||
к |
неподвижной оси равна половине произведения |
|||||||||||||||||
осевого момента инерции на квадрат угловой |
||||||||||||||||||
|
||||||||||||||||||
O |
скорости. |
плоскопараллельном |
|
движении |
||||||||||||||
|
При |
|
||||||||||||||||
|
твердого тела (рис. 17.2) примем центр масс С |
|||||||||||||||||
Рис. 18.1 |
за |
полюс |
и |
воспользуемся |
теоремой |
Кенига |
||||||||||||
|
(18.3). В этом случае относительное движение |
|||||||||||||||||

является вращением вокруг оси, проходящей через центр масс С с угловой скоростью ω . Тогда второе слагаемое (18.3) имеет вид
T |
I |
C |
ω2 |
, |
(18.6) |
|
|
|
|||
вр |
|
|
2 |
||
|
|
|
|
|
где IС момент инерции тела относительно оси, проходящей через центр масс С перпендикулярно плоскости движения. Подставив (18.6) в (18.3), получаем
Т |
M V 2 |
|
I |
C |
ω2 |
|
|
C |
|
|
. |
(18.7) |
|||
2 |
|
|
2 |
||||
|
|
|
|
|
|
При плоскопараллельном движении кинетическая энергия тела складывается из кинетической энергии поступательного движения тела с центром масс и кинетической энергии вращательного движения вокруг оси, проходящей через центр масс перпендикулярно плоскости движения.
Если механическая система состоит из нескольких твердых тел, то следует вычислить кинетическую энергию каждого тела, а затем полученные значения сложить.
Теоремы об изменении кинетической энергии
Определение кинематических характеристик точек и тел механической системы удобно проводить с использованием теоремы об изменении кинетической энергии. Согласно (15.1) для любой к-й точки системы основной закон динамики имеет вид
|
|
|
|
r |
е |
|
i |
, |
|
(к = 1, 2, …, n). |
(18.8) |
|
|
|
mкaк |
Fк |
Fк |
|
|||||
Здесь |
|
|
|
|
|
|
r |
|
|
r |
|
|
r |
dV |
|
dV |
|
|
dV |
|
|||
|
|
dr |
|
|
|||||||
|
aк |
|
к |
|
rк |
|
к |
|
rк |
Vк. |
(18.9) |
|
|
|
dt |
|
drк |
|
dt |
|
drк |
|
|
С учетом (18.9) уравнение (18.8) принимает вид |
|
|
|
||||||||
r |
dV |
|
r е |
r i |
|
|
|
|
|
|
|
mкVк |
rк |
Fк |
Fк |
|
(к = 1, 2, …, n) |
|
|||||
или |
drк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
|
mк Vк dVк |
е |
|
i |
, |
|
(к = 1, 2, …, n). |
(18.10) |
||||
Fк |
drк Fк |
drк |
|
||||||||
Внося mк Vк в (18.10) |
под |
знак дифференциала и воспользовавшись |
|||||||||
определением элементарной работы (17.1), получаем
|
mк Vк |
2 |
dAке |
dAкi , |
|
|
|
d |
|
|
(к = 1, 2, …, n), |
(18.11) |
|||
2 |
|
||||||
|
|
|
|
|
|
|
|
где dAке иdAкi элементарные работы соответственно внешних и внутренних
сил, действующих на к-ю точку системы. Складывая n уравнений (18.11), получим
|
n |
2 |
|
n |
|
n |
|
d |
|
mк Vк |
|
dAке |
|
dAкi |
|
2 |
|||||||
|
к 1 |
|
к 1 |
|
к 1 |
||
или |
|
n |
|
n |
|
|
|
|
|
|
|
|
|||
dT |
dAке |
dAкi . |
(18.12) |
||||
|
|
к 1 |
|
к 1 |
|
|
|
Равенство (18.12) представляет теорему об изменении кинетической |
|||||||
энергии системы в дифференциальной форме: дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних сил, действующих на систему.
Если обе части равенства (18.12) проинтегрировать в пределах, соответствующих перемещению системы из начального положения с кинетической энергией Т0 в конечное положение, в котором кинетическая энергия равна Т1, то получим уравнение
n |
|
n |
|
T1 Т0 Aке |
|
Aкi , |
(18.13) |
к 1 |
|
к 1 |
|
выражающее теорему об изменении |
кинетической |
энергии системы |
|
в интегральной форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ всех внешних и внутренних сил, приложенных к системе на этом перемещении.
В случае неизменяемой системы (абсолютно твердое тело), вследствие выполнения теоремы (3.9), сумма работ внутренних сил равна нулю:
n
Aкi 0 . Сумма работ внутренних сил натяжения гибкой нерастяжимой
к 1
нити, связывающей тела системы, также равна нулю. В этих случаях выражение (18.13) принимает более простой вид
n |
|
T1 Т0 Aке . |
(18.14) |
к 1
Следовательно, для неизменяемой системы в правую часть (18.14) входит только работа внешних сил, действующих на систему. Данное обстоятельство позволяет исключить из рассмотрения внутренние силы,
которые обычно неизвестны, что значительно упрощает решение практических задач.
Для одной материальной точки теорему (18.14) можно записать в виде
mV 2 |
|
mV 2 |
n |
, |
(18.15) |
|
1 |
2 |
0 |
Aк |
|||
2 |
|
|
к 1 |
|
|
|
где V0 и V1 величины скорости |
точки |
соответственно |
в начальном и |
|||
конечном ее положениях. |
|
|
|
|
|
|
Теоремой об изменении кинетической энергии системы в интегральной |
||||||
форме удобно пользоваться |
для |
определения линейных |
скоростей точек |
|||
и угловых скоростей тел по заданному перемещению механической системы. Рассмотрим случай, когда система движется в стационарном
потенциальном силовом поле.
Согласно (17.22) потенциальная энергия П механической системы в данном ее положении равна работе, которую произведут силы поля при перемещении точек системы из данного положения в нулевое:
n |
|
П АBкOк . |
(18.16) |
к 1 |
|
Если на систему действует несколько полей, то для каждого поля можно выбрать свою «нулевую точку» О отсчета.
Пусть все действующие на систему внешние и внутренние силы являются потенциальными. Тогда с учетом (17.20) работа всех сил при перемещении системы из начального в конечное положение определяется выражением:
n |
n |
|
Aке |
Aкi П0 П1 , |
(18.17) |
к 1 |
к 1 |
|
где П0 и П1 значения потенциальной энергии системы соответственно в начальном и конечном положениях. Подставляя (18.17) в (18.13), получим
Т1 Т0 П0 П1 |
|
или |
|
Т1 П1 П0 Т0 Е const , |
(18.18) |
где Е Т П полная механическая энергия системы.
Равенство (18.18) выражает закон сохранения механической энергии системы: при движении системы под действием потенциальных сил полная механическая энергия системы в каждом ее положении есть величина постоянная. Следовательно, Е является интегралом движения. Механическая
система, для которой выполняется закон сохранения механической энергии
(18.18) называется консервативной системой.
При движении механической системы в реальных условиях наличие сил сопротивления движению приводит к уменьшению полной механической энергии, т. е. движение все время сопровождается рассеиванием (диссипацией) энергии. Силы (сопротивления движению, трения), приводящие к диссипации энергии, называются диссипативными силами, а механическая система, на которую действуют такие силы диссипативной системой. Потерянная системой за счет работы сил сопротивления часть механической энергии переходит в другие виды энергии. При этом полная энергия всех видов (механическая, тепловая, химическая и т. д.) остается постоянной.
ЛЕКЦИЯ 19 ДИНАМИКА ТВЕРДОГО ТЕЛА
Дифференциальные уравнения движения твердого тела
Применим общие теоремы динамики к получению дифференциальных уравнений движения твердого тела. Рассмотрим простейшие случаи движения твердого тела.
1. Поступательное движение твердого тела. Из теоремы о движении центра масс (15.5) имеем
|
|
|
r |
n r |
е |
|
|
|
|
|
|
M aC |
Fк . |
|
|
|
|||
|
|
|
|
к 1 |
|
|
|
|
|
Однако при |
поступательном |
движении |
|
ускорения |
всех |
точек тела |
|||
геометрически |
равны, |
т. е. |
aC a , |
|
|
|
|
|
ускорение |
где a |
xi yj |
zk |
|||||||
произвольной точки тела. Тогда (15.5) принимает вид: |
|
|
|||||||
|
|
|
r |
n r е |
, |
|
|
|
|
|
|
|
M a Fк |
|
|
|
|
||
|
|
|
|
к 1 |
|
|
|
|
|
или в проекции на координатные оси получаем |
|
|
|
||||||
|
n |
|
n |
|
|
|
n |
|
|
M &x Fкхе , |
M &y Fкеy |
, |
M &z Fкеz . |
(19.1) |
|||||
|
к 1 |
|
к 1 |
|
|
|
к 1 |
|
|
Уравнения (19.1) называются дифференциальными уравнениями поступательного движения твердого тела в декартовых координатах.
2. Вращательное движение твердого тела. Рассмотрим твердое тело,
вращающееся вокруг неподвижной оси z, под действием сил F1е, F2e , ..., Fne
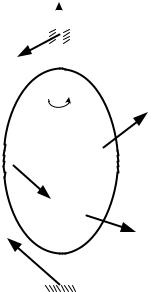
(рис. 19.1). Кроме этих сил на тело действуют реакции RA подпятника А и RB
подшипника В.
Воспользуемся теоремой об изменении кинетического момента системы относительно оси вращения z тела (16.15):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dK |
|
|
n |
r e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
mz (Fi ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(19.2) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В правой части (19.2) отсутствуют моменты |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||||||||||||||
реакций |
RA и |
|
|
RB , |
так как они равны нулю |
|
|
|
|
|
|
|
|
В |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
RB |
|
|
|
|
|
|
|||||||||||||||||||||||||||
(реакции RA и |
|
RB пересекают ось z). |
Согласно |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
(16.9) для вращающегося тела Kz |
Iz |
ω , где для |
|
|
|
|
|
|
|
|
|
|
|
|
e |
||||||||||||||||||||||
твердого |
тела |
Iz |
const . |
Подставляя |
(16.9) в |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|||||||||||||||||||||||
(19.2), находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
I |
|
dω |
|
|
n |
m |
|
r e |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
( F |
|
|
|
|
(19.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
z |
dt |
|
|
|
z |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fne |
|
|
|
|
|
|
|
e |
||||||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
dω |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||||||||
или, поскольку |
&, получаем |
|
|
|
|
|
A |
|
|
|
|
А |
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
& |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 19.1 |
|||||||||||||
|
z |
|
z |
|
( F e ) . |
|
|
|
|
|
|
(19.4) |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (19.4) называется дифференциальным уравнением |
||||||||||||||||||||||||||||||||||
вращательного |
|
движения твердого |
тела. Иногда вводится |
|
обозначение |
||||||||||||||||||||||||||||||||
n |
m |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
( F e ) Me |
|
, |
где |
величина |
|
e |
называется вращающим моментом. |
||||||||||||||||||||||||||||
|
i |
|
|
|
|
z |
|
Mz |
|||||||||||||||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда, так как & ε |
угловое ускорение тела, (19.4) принимает вид |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iz ε Mez |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(19.5) |
||||||
т. е. произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающему моменту. Из сравнения (19.5) с основ-
ным законом динамики (10.1) можно заключить, что момент инерции тела относительно оси его вращения играет такую же роль, как и масса точки при
ее движении. Следовательно, Iz является мерой инертности тела при
вращательном движении.
Из уравнения (19.4) можно:
1) зная закон вращения (t) , найти Mez ;
2) зная вращающий момент Mez , определить закон вращательного
движения тела вокруг неподвижной оси (t) , т. е. решить основную задачу динамики для твердого тела. В частности,
а) если Mez 0 , то ω ω0 const , и тело вращается равномерно по закону 0 ω0 t ;
б) если Mez const , то ε const2 , и тело совершает равнопеременное
вращение по закону 0 ω0 |
t |
|
ε |
|
t2 |
. |
|
|
|||||
|
|
|
|
|||
|
2 |
|||||
|
|
|
|
|||
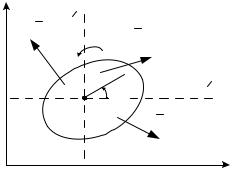
3. Плоскопараллельное движение твердого тела. Пусть свободное тело совершает плоское движение относительно неподвижной плоскости Оху
под действием внешних сил F1е , F2e ,...., Fne и имеет в данный момент времени
угловое ускорение ε (рис. 19.2). Примем за полюс центр масс С тела. Тогда его движение можно рассматривать как слагающееся из поступательного движения вместе с центром масс С и вращательного движения вокруг оси Cz , перпендикулярной плоскости Оху и движущейся поступательно вместе с подвижной системой отсчета Cx y z .
y |
Fn |
y |
e |
|
|
|
F2 |
|
|
|
|
|
||
yC |
|
|
|
x |
|
C |
|
||
|
|
|
F1 |
|
|
|
|
|
|
O |
|
xC |
|
x |
|
|
Рис. 19.2 |
|
|
Если хС и уС координаты центра масс С в неподвижной системе отсчета Оху, то по теореме о движении центра масс (13.14) получим два дифференциальных уравнения, характеризующих поступательное движение тела вместе с центром масс С:
M &x |
n |
, |
M &y |
n |
, |
F е |
F е |
||||
C |
кх |
|
C |
кy |
|
|
к 1 |
|
|
к 1 |
|
где М масса тела.
Третье дифференциальное уравнение, определяющее вращательное движение вокруг оси Cz , получаем из (19.4):
I |
|
& |
n |
m |
|
r |
|
С |
|
С |
( F e ) |
, |
|||
|
|
|
i |
||||
|
|
|
i 1 |
|
|
|
|
поскольку согласно (16.18) вид теоремы моментов, с помощью которой была получена формула (19.4), не изменится в системе координат Cx y z ,
движущейся поступательно с центром масс С тела.
Тогда окончательно находим дифференциальные уравнения плоскопараллельного движения твердого тела:
