u_lectures

Общее уравнение динамики (21.20) впервые было установлено Лагранжем. Оно содержит в себе всю информацию о движении механической системы под действием заданных активных сил. Соотношение (21.20) на самом деле не является одним уравнением, а содержит в себе количество уравнений, равное числу S степеней свободы системы, которое соответствует числу независимых возможны перемещений.

Общее уравнение динамики (21.20) также называется принципом Даламбера–Лагранжа. Он заключается в том, что соотношение (21.20) устанавливает необходимое и достаточное условие действительного движения механической системы: истинное движение из всех кинематически возможных выделяется тем, что для него и только для него в данный момент времени сумма элементарных работ активных сил и сил инерции на любых возможных перемещениях равна нулю. Следует подчеркнуть, что этот принцип можно использовать в качестве основной аксиомы механики, так как из него можно вывести как уравнения равновесия, прировняв модули сил инерции точек системы нулю, так и дифференциальные уравнения движения механической системы.

Важным свойством общего уравнения динамики (21.20) является то, что оно не содержит реакций идеальных связей. Это позволяет, решить задачу о движении механической системы, не определяя этих реакций.

Отметим, что общее уравнение динамики может быть применено и для неидеальных связей, наложенных на систему. В этом случае с учетом разложения сил реакций на нормальные составляющие и силы трения можно воспользоваться уравнением (21.20), отнеся силы трения к активным силам, действующим в системе. Это, в свою очередь, приводит к необходимости введения экспериментального закона трения, с помощью которого устраняется несоответствие числа уравнений и числа неизвестных в них при не-идеальных связях.

ЛЕКЦИЯ 22

Обобщенные координаты и обобщенные силы

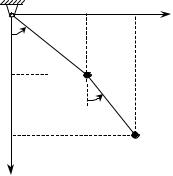
Для введения понятия обобщенных координат рассмотрим плоский двойной математический маятник, состоящий из двух невесомых стержней длиной l1 и l2 с точечными массами M1 и M2 на концах (рис. 22.1). Система обладает двумя степенями свободы. Действительно стержень ОМ1 может вращаться вокруг неподвижной горизонтальной оси О, перпендикулярной плоскости движения хОу, а стержень M1M2 – вокруг горизонтальной оси, проходящей через точку M1, в той же плоскости. Поэтому уравнения связей имеют вид

Здесь углы 1 и 2 играют роль независимых параметров, однозначно определяющих положение рассматриваемой механической системы.

Пусть теперь имеется система n материальных точек, на которую наложены k голономных связей, заданных уравнениями (20.2). Поскольку число степеней свободы равно S, то введем независимые переменные q1, q2,

..., qs. Тогда для рассматриваемой системы соотношения (22.1) примут вид

x = x (q1, q2, ..., qs, t);

Отметим, что независимые координаты qm(m = 1, 2, …, s) – это не обязательно набор S переменных из числа декартовых координат x , у , z . Ими могут быть переменные другой природы, так в приведенном выше примере вместо декартовых координат введены угловые координаты.

S независимых параметров q1, q2, ..., qs однозначно определяющих положение точек материальной системы, совместимое со связями, называются обобщенными координатами.

на декартовые оси могут быть выражены через потенциальную энергию П системы согласно формулам (17.18):

Для механической системы, находящейся в потенциальном силовом поле, обобщенная сила Qm определяется взятой с обратным знаком частной

производной от потенциальной энергии по соответствующей обобщенной координате:

Отметим, что размерность обобщенной силы равна размерности работы, деленной на размерность обобщенной координаты.

Принцип возможных перемещений в обобщенных координатах

Согласно принципу возможных перемещений (21.12), необходимым и достаточным условием равновесия голономной материальной системы, подчиненной идеальным стационарным связям, является равенство нулю возможной работы действующих активных сил, A = 0. В обобщенных координатах для системы с S степенями свободы это условие с учетом (22.5) принимает вид

Поскольку q1, q2, ..., qs – независимые вариации обобщенных координат, то выражение (22.9) выполняется только тогда, когда все обобщенные силы одновременно равны нулю, т. е.

Уравнения (22.10) выражают принцип возможных перемещений в обобщенных координатах: для равновесия материальной системы

необходимо и достаточно, чтобы все обобщенные силы, соответствующие выбранным для системы обобщенным координатам, были равны нулю.

Если обобщенные силы зависят не только от обобщенных координат, но и от обобщенных скоростей q&1 , q&2 , ..., qs , то в (22.10) все обобщенные

скорости нужно приравнять нулю. Из (22.10) следует, что количество уравнений равновесия равно числу обобщенных координат, т. е. числу S степеней свободы системы.

Для консервативной системы условия равновесия (22.10) имеют вид

Полный дифференциал потенциальной энергии П(q1, q2, ..., qs) системы определяется выражением

Условие (22.12) означает, что в положении равновесия потенциальная энергия консервативной системы принимает экстремальное значение.

Следовательно, решения системы уравнений (22.11)–(22.12) определяют обобщенные координаты q10 , q20 , ..., qS0 , соответствующие положению

равновесия системы.

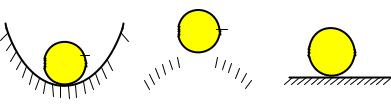
Положение равновесия системы может быть устойчивым, неустойчивым и безразличным. Например, физический маятник (рис. 19.3, а) имеет два возможных положения равновесия – это положения, при которых центр масс маятника находится в верхней и нижней точках своей траектории. Очевидно, что верхнее положение равновесия маятника практически нельзя осуществить, оно является неустойчивым; нижнее положение легко реализуемо, это устойчивое положение равновесия.

Устойчивость или неустойчивость положения равновесия определяется поведением системы при воздействии на нее малых возмущений.

Если при достаточно малых отклонениях от положения равновесия или достаточно малых начальных скоростях система во все время движения не выходит из пределов сколь угодно малой заданной окрестности положения равновесия, имея при этом сколь угодно малые скорости, то это положение равновесия является устойчивым.

Уравнения (23.14) называются уравнениями Лагранжа второго рода.

Уравнения Лагранжа (23.14) содержат S + 1 функций, которыми являются кинетическая энергия T системы и обобщенные силы Q1, Q2, ..., Qs. Чтобы воспользоваться уравнениями Лагранжа (23.14), следует выразить эти функции через обобщенные координаты q1, q2, ... , qS и обобщенные скорости

Основные преимущества уравнений Лагранжа второго рода:

1)по форме уравнения (23.14) записывают одинаково в любой системе координат, и различие в выборе координат сказывается лишь на виде S + 1 функций, входящих в эти уравнения. Следовательно, уравнения Лагранжа второго рода ковариантные относительно любого точечного преобразования координат;

2)число уравнений (23.14) не зависит от количества материальных точек, входящих в систему, и от характера их движения, а определяется только числом S ее степеней свободы;

3)для материальной системы с идеальными связями (20.11) правые части уравнений Лагранжа (23.14) содержат только обобщенные активные силы, тем самым из рассмотрения исключаются реакции связей, которые, как правило, неизвестны.

В математическом отношении уравнения (23.14) представляют собой систему S дифференциальных уравнений второго порядка. Нетрудно показать, что эта система может быть представлена в форме Коши, т. е. разрешена относительно старших производных. Для таких систем имеет место теорема о существовании и единственности решения. Из нее следует детерминированность движения материальной системы, как только заданы начальные условия движения, т. е. в начальный момент зафиксированы значения обобщенных координат и обобщенных скоростей:

Решение основной задачи динамики заключается в интегрировании системы уравнений Лагранжа (23.14), т. е. в нахождении обобщенных координат q1, q2, ..., qS как функций времени t: