Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусско-Российский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

u_lectures

.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

1.62 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Здесь		r			r
	drM			drA
		V	,		V	A ,	(4.4)

	dt	M		dt

dt i

k x

(4.5)

где

(4.6)

– относительная скорость точки М в подвижной системы отсчета Ахуz. Поскольку векторы i , j , k постоянные по модулю ( i j k 1 ), но

меняющие свое направление с угловой скоростью ωe , то согласно (2.18) получим формулы Пуассона:

di	r	r	dj	r	r	dk	r	r
dt	ωe i ;		dt	ωe j ;		dt	ωe k .
dt			dt			dt

Тогда с учетом (4.6), (4.7) и (4.2) выражение (4.5) принимает вид

dρ	r	r	r	r	r	r	r
dt	Vr ωе ix ωе jy ωе kz
	r	r	r	r	r		r	r	r

	Vr ωе xi			yj zk			Vr	ωе ρ.

Подставляя (4.4) и (4.8) в (4.3) получаем

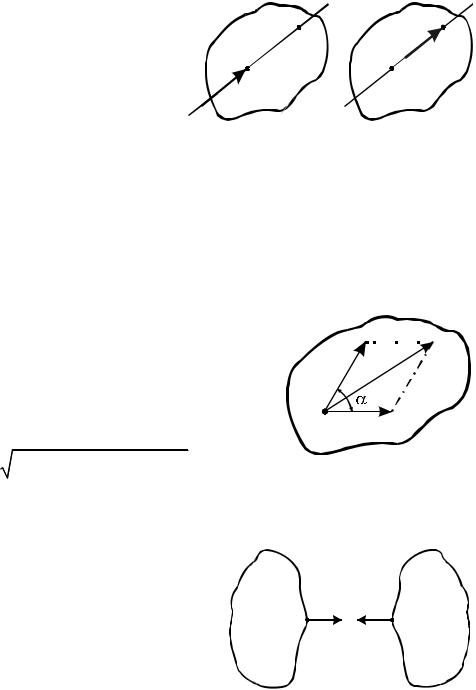
Va VА Vr ωе

ρ.

(4.7)

(4.8)

(4.9)

Мысленно остановим относительное движение (Vr 0 ), тогда точка М участвует только в переносном движении вместе телом D, и ее абсолютная скорость равна переносной скорости Va Vе . Подставляя эти условия в (4.9) получаем выражение для переносной скорости точки М:

Ve VА ωе

ρ.

(4.10)

Следовательно, переносная скорость равна скорости точки свободного твердого тела D, с которой в данный момент времени совпадает точка М.

С учетом (4.10) выражение (4.9) принимает вид

Vr	Va	Va Vе Vr ,	(4.11)
	Va
		где вектор абсолютной скорости Va	определяется
M	Ve	где вектор абсолютной скорости Va	определяется
M		диагональю параллелограмма, построенного на
		диагональю параллелограмма, построенного на
		векторах переносной и относительной скоростей
Рис. 4.3		как на сторонах (рис. 4.3). Модуль абсолютной
		скорости определяется по теореме косинусов:

Ve2

Vr2 2Ve Vr cosα ,

(4.12)

где угол между векторами Ve

и Vr .

Из (4.12) следуют частные случаи:

1) если = 0,

;

(4.13)

если = π,

;

(4.14)

если = π/2, Va Ve2 Vr2 .

(4.15)

Следовательно, для определения абсолютной скорости необходимо знать модули и направления переносной и относительной скоростей.

Теорема Кориолиса о сложении ускорений

Абсолютное ускорение точки при сложном движении определяется при помощи теоремы Кориолиса: абсолютное ускорение точки равно геометрической сумме переносного, относительного ускорений и ускорения Кориолиса.

Доказательство. Пусть ускорение точки А тела D равно аA , а его угловая скорость и угловое ускорение в данный момент времени соответственно – ωe и εe . Найдем абсолютное ускорение аа точки М,

движущейся относительно тела D. Вычислим производную по времени от равенства (4.9):

dω

dρ

ρ ωе

r .

Поскольку

dω

A ,

εe

то с учетом (4.6) и (4.8) имеем

r r

dx r

dz r

aa aA

εe ρ

ωe Vr

ωe ρ

d 2 x r

d 2 y r

d 2 z

aA εe ρ ωe ωe

ωe

dt2

(4.16)

dx di

dy dj

dz dk .

dt dt

Так как относительное ускорение точки М в подвижной системе координат

Ахуz

d 2 x r

d 2 y r

d 2 z

(4.17)

k ,

то, подставляя (4.17), (4.7) в (4.16), получаем

r r

dx r

dy r

dz r

aa aA e e e e Vr

dt e

e j dt e k

dx r

dy r

dz r

(4.18)

aA e e e e Vr ar e

k .

Поскольку

то (4.18) принимает вид

aa aA εe ρ ωe ωe ρ ar

2 ωe Vr .

(4.19)

Если остановить относительное движение (Vr 0, ar 0 ), тогда абсолютное ускорение точки М равно ее переносному ускорению aa aе . Подставляя эти условия в (4.19), получаем выражение для переносного ускорения точки М:

ae aA εe ρ ωe ωe ρ.

Последнее слагаемое в (4.19) является ускорением Кориолиса:

aС 2 ωe Vr .

(4.20)

(4.21)

Следовательно, с учетом (4.20) и (4.21) теорема Кориолиса (4.19) принимает вид

aa aе ar aC ,

(4.22)

что и требовалось доказать.

Модуль ускорения Кориолиса (4.21) вычисляется по формуле

r	Vr sin α.	(4.23)
aС 2 ωe

Из (4.23) следуют частные случаи, когда ускорение Кориолиса равно нулю, и абсолютное ускорение точки вычисляется по формуле aa aе ar :

1)aС 0, если ωe 0 , т. е. переносное движение поступательное;

2)aС 0, если Vr 0 , т. е. в точках остановки относительного движения;

3)aС 0, если sin α 0 , т. е. векторы ωе и Vr коллинеарные.

Появление ускорения Кориолиса связано с изменением абсолютной скорости, обусловленным двумя причинами:

1) влиянием переносного движения на относительную скорость (при ωе 0 вектор Vr поворачивается относительно абсолютной системы

координат за счет вращения подвижной системы – тела D);

2) влиянием относительного движения на переносную скорость (при

Vr 0 положение точки в подвижной системе координат изменяется и, следовательно, изменяется переносная скорость).

Согласно определению (4.21) вектор ускорения Кориолиса aС

направлен перпендикулярно плоскости, проходящей через векторы ωе и Vr в

ту сторону, откуда кратчайшее совмещение первого вектора с вторым видно происходящим против хода часовой стрелки (рис. 4.4).

Направление вектора ускорения Кориолиса можно также найти по правилу Жуковского. Для этого следует (см. рис. 4.4):

1) спроецировать вектор

относительной

скорости

на

плоскость

перпендикулярную

вектору ωе ;

эту проекцию Vr

90o

2) повернуть

в плоскости Q на

90 в

направлении

переносного вращения ωе .

случае,

когда

вектор

Рис. 4.4

относительной

скорости

лежит

плоскости Q (

= 90 ),

для определения направления вектора aC

достаточно повернуть вектор Vr в плоскости Q на 90

в сторону

переносного вращения (по направлению ωе ).

Модуль абсолютного ускорения точки при сложном движении определяется аналитически. Для этого сначала находят модули и

направления векторов aе, ar и aC . Затем проецируют теорему Кориолиса (4.22) на оси неподвиж-ного трехгранника ОХYZ и по найденным проекциям

абсолютного ускорения aaX ,	aaY	и aaZ	на эти	оси вычисляют модуль
абсолютного ускорения точки
aa	aaX2	aaY2	aaZ2 .	(4.24)

МОДУЛЬ 2. СТАТИКА

ЛЕКЦИЯ 5. ВВЕДЕНИЕ В СТАТИКУ

Статикой называется раздел механики, в котором излагается учение о силах и исследуются условия равновесия материальных тел, находящихся под действием сил.

Под равновесием понимают состояние покоя тела по отношению

кинерциальной системе отсчета, связанной обычно с неподвижным телом.

Вкачестве модели реального материального тела в статике рассматривается

абсолютно твердое тело тело, расстояние между любыми точками которого не изменяется.

Мерой механического взаимодействия материальных тел является

сила. Сила F векторная величина, действие которой на тело определяется модулем, направлением и точкой приложения.

Прямая линия, вдоль которой направлен вектор F , называется линией действия силы.

Совокупность сил, действующих на тело, называется системой сил. Если линии действия сил лежат в одной плоскости, то система сил называется плоской.

Если линии действия сил не лежат в одной плоскости, то система сил является пространственной. Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Две системы сил, оказывающие на тело одинаковое действие,

называются эквивалентными.

Система сил, под действием которой свободное твердое тело находится в покое, называется уравновешенной или эквивалентной нулю.

Аксиомы статики

В основе статики лежат аксиомы экспериментально установленные

			законы, справедливость которых	проверена
		F1	законы, справедливость которых	проверена
		F1	практической деятельностью.
			практической деятельностью.
	B		Аксиома 1. Если на свободное абсолютно
	A		твердое тело действуют две силы,	то тело
	A		может находиться в равновесии только тогда,
			может находиться в равновесии только тогда,
			когда эти силы равны по модулю, и направлены
F2			когда эти силы равны по модулю, и направлены

Рис. 5.1

вдоль одной прямой в противоположные стороны (рис. 5.1):

F1 F2 .

Силы F1 и F2 являются уравновешенными.

Аксиома 2. Действие данной

системы сил на абсолютно твердое					B		B
тело не изменится, если		к	ней
тело не изменится, если		к	ней	A			F
добавить	или	отнять				A	F
добавить	или	отнять				A
уравновешенную систему сил.
уравновешенную систему сил.				F
Следствие.	Не	нарушая		F
Следствие.	Не	нарушая
состоя-ния твердого тела, силу
можно переносить по линии ее						Рис. 5.2
действия в любую точку тела,			т. е.

сила вектор скользящий (рис. 5.2).

Аксиома 3. Две силы, приложенные к телу в одной точке, можно заме-нить одной силой, приложенной в той же точке и изображаемой диагональю параллелограмма, построенного на этих силах как на сторонах

(рис. 5.3):

R F1 F2 .

(5.1)

Сила R эквивалентная системе сил F1 и F2

называется равнодействующей:

R ~ F1

, F2 .

Модуль ее вычисляется по формуле

F12 F2

2F1F2 cosα ,

(5.2)

Рис. 5.3

где угол между силами F1 и F2 .

Аксиома 4. Силы, с которыми два

тела действуют друг на друга, равны по

модулю и направлены по одной прямой

в противоположные стороны (рис. 5.4):

FА FВ .

Силы FA и

не

образуют

уравновешенную систему сил, так как они	Рис. 5.4

приложены к разным телам.

Аксиома 5. Равновесие деформируемого тела не нарушится, если его считать отвердевшим (абсолютно твердым).

Две основные задачи статики. В статике решаются две задачи:

1)задача о приведении системы сил заключается в замене данной системы сил другой, более простой, ей эквивалентной;

2)задача о равновесии состоит в определении условий, при которых система сил, приложенная к телу, будет уравновешенной системой.

Связи и их реакции

Тело, перемещениям которого в пространстве препятствуют какиенибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все, что ограничивает перемещение данного тела в пространстве, называется связью.

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

Одним из основных положений теоретической механики является

принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями связей.

В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного, находящегося под действием активных (заданных) сил и реакций связей.

NC TATB

B C A B


		NB
		NB
	NA
Рис. 5.5			Рис. 5.6
Рис. 5.5

Рассмотрим наиболее часто встречающиеся типы связей и направления их реакций.

1.Гладкая плоскость (поверхность) или опора. Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке (рис. 5.5).

2.Гибкая нить (провода, канаты, цепи, ремни). Реакция Т нити направлена от тела вдоль нити к точке подвеса (рис. 5.6).

3.Невесомый стержень с шарнирами. Реакция N шарнира направлена

вдоль невесомого стержня. Обычно реакция N изображается от тела по стержню в предположении, что в равновесии стержень растянут (рис. 5.7).

4. Неподвижный цилиндрический шарнир (подшипник). Реакция RA

цилиндрического шарнира лежит в плоскости Аху перпендикулярной оси

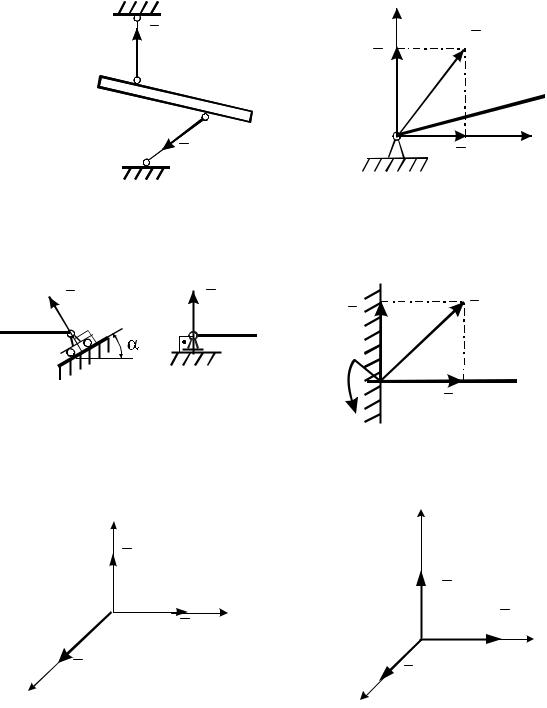
шарнира и может иметь любое направление. Обычно RA раскладывают в
точке А на две взаимно перпендикулярные составляющие ХA и YA (рис. 5.8).
		NA			y
		NA				R
		A			YA	A
		A			YA
			B		A		x
			NB		A	XA
			NB			XA
		Рис. 5.7				Рис. 5.8
	RB		RB		Y	RA
	B		B		A
		Рис. 5.9		mA	A	XA
					A

					Рис. 5.10
	1	z	3		z	1
			3
		ZA
2		ZA			2
2			y		2	ZA
			y			ZA
		A	YA		A	Y	y
			YA		A	A
x	XA				X	3
x					A
		Рис.5.11			Рис. 5.12
					Рис. 5.12
5. Шарнирно-подвижная опора (опора на катках). Реакция RВ
проходит через ось шарнира В и направлена перпендикулярно к опорной
поверхности (рис. 5.9).

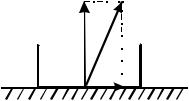
6.Жесткая заделка. Нахождение реакции жесткой заделки сводится

копределению составляющих ХA и YA препятствующих линейному

перемещению точки А балки в плоскости действия активных сил и алгебраической величины реактивного момента mA, препятствующего вращению балки под действием заданных сил (рис. 5.10).

7. Сферический шарнир. Сферическим шарниром называется устройство (рис. 5.11), которое допускает сферическое движение тела 3 вокруг неподвижной точки А центр внутренней сферы 1, с которой жестко скреплено рассматриваемое тело 3. При условии, что сферическая

поверхность идеально гладкая, реакция RА направлена в точке А по нормали к этой поверхности. Обычно на схемах реакцию RА сферического шарнира раскладывают на три взаимно перпендикулярные составляющие ХA , YA , ZA ,

неизвестные по величине.

8. Подпятник. Подпятник (рис. 5.12) представляет собой соединение цилиндрического шарнира 2 с опорной плоскостью 3, на которую опирается

вал 1. Реакция подпятника складывается

из реакции цилиндрического

подшипника, которая раскладывается в плоскости

перпендикулярной

его

оси

на

две

взаимно

перпендикулярные

составляющие

ХA

и YA , и

нормальной реакции ZA

опорной плоскости 3.

9. Шероховатая неподвижная поверхность.

Реакция шероховатой поверхности представляет

Fтр

собой равнодействующую R

силы нормальной

Рис. 5.13

реакции N и силы трения Fтр

(рис. 5.13).

Проекция силы на ось и на плоскость

С математической точки зрения описание сил в статике эквивалентно описанию векторов в векторной алгебре. Рассмотрим основные положения.

Проекцией силы F на ось называется алгебраическая величина равная произведению модуля силы на косинус угла между вектором силы и

положительным направлением оси:
	Fx F cosα,	(5.3)
где F модуль силы F ; α	угол между вектором F	и положительным
направлением оси х.

Fx 0

Рис. 5.14

Проекция силы является:

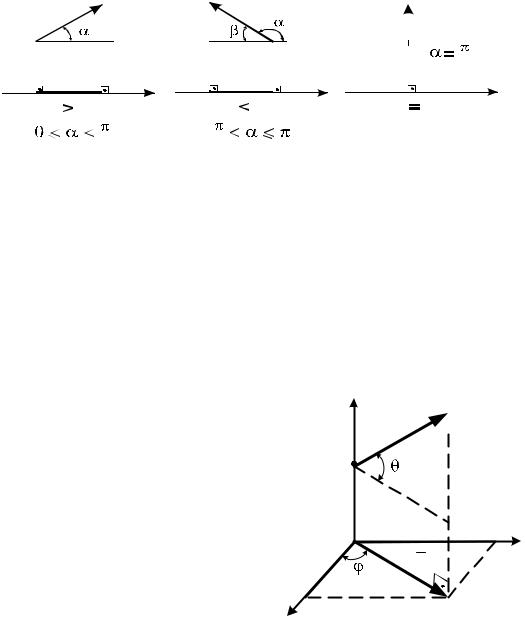
1) положительной ( Fx

0 ), если угол α острый (рис. 5.14, а);

2) отрицательной ( Fx

0 ), если угол α

тупой (рис. 5.14, б), так как

Fx F cosα F cos 180о β F cosβ;

3) равняется нулю ( Fx 0 ), если угол α

(рис. 5.14, в).

Проекцией силы

F на плоскость

Оху называется

вектор

Fху ОВ1 ,

заключенный			между		проекциями			A
начала	и	конца		силы	F	на	эту

плоскость (рис. 5.15), где					Fху	F cosθ.			Fy	B3	y
В		случае			произвольной			O
ориентации		силы		в пространстве			ее	F	F
проекцию на координатные оси обычно
								x	xy
определяют			методом			двойного		B2		B1
проецирования.				Сначала		силу		x
проецируют на одну из координатных									Рис. 5.15
осей	(например			ось	z)	и	на

координатную			плоскость		двух других

осей (на Оху), проекция силы на плоскость Fху является вектором, который

затем проецируют на оси координат Ох и Оу, расположенные в плоскости

(рис. 5.15):

Fх ОВ2 Fху cos F cosθ cos ,

Fy ОВ3 Fху sin F cosθ sin ,

Fz F sin θ .

Аналитический способ задания силы

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.11.2018216.58 Кб17Testy_po_blokam.doc
#
25.09.2019819.2 Кб3Testy_s_otvetami.doc
#
29.02.201624.58 Кб8titulnik.doc
#
14.04.20192.05 Mб8TM_shpory.doc
#
06.05.2019351.58 Кб8Ukaz_Prezidenta_Respubliki_Belarus_ot_18_iyulya...docx
#
29.02.20161.62 Mб9u_lectures.pdf
#
16.07.201960.42 Кб1VARA.doc
#
11.11.201992.16 Кб2VBA_№5.doc
#
27.09.2019137.78 Кб2Visam_ind_2.docx
#
20.04.2019671.23 Кб5Voprosy и ответы.doc
#
26.04.2019317.38 Кб0voprosy_po_tfp_otvety_1-81 (1).docx