2.7. Преобразования координат
Пусть координаты точки заданы в правой системе
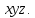
Требуется найти координаты этой точки в правой системе
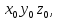
по отношению к которой определенным образом движется система
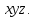
Координаты точки занесем в соответствующие матрицы следующего вида:
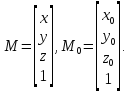
Тогда преобразование координат можно представить в матричном виде
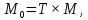
где
‑это т. н. матрица преобразования, которая зависит от того, как движется система
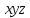
относительно системы
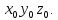
Любое движение системы
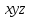
относительно системы
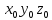
можно представить как комбинацию любого количества следующих составляющих движений, каждому из которых соответствует своя матрица преобразования:поступательного движения, поворота вокруг оси абсцисс, поворота вокруг оси ординат и поворота вокруг оси аппликат.Матрица, соответствующая результирующему движению, состоящему из
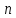
последовательных движений, определяется следующим образом:
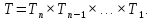
В этом матричном выражении в общем случае следует соблюдать порядок перемножения матриц, соответствующий очередности осуществляемых движений.
Поступательное движение. Этот вид движения можно задать при помощи вектора перемещения
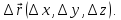
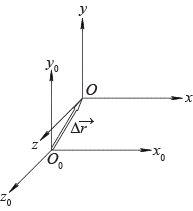
Матрица этого преобразования имеет вид
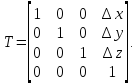
Поворот вокруг оси абсцисс на угол
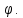
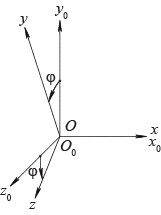
При этом положительное направление отсчета угла
‑ направление, противоположное направлению хода часовой стрелки, если смотреть со стороны положительного направления оси абсцисс.
Матрица этого преобразования:
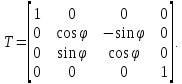
Поворот вокруг оси ординат на угол
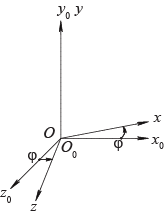
При этом положительное направление отсчета угла
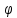
‑ направление, противоположное направлению хода часовой стрелки, если смотреть со стороны положительного направления оси ординат.
Матрица этого преобразования:
Поворот вокруг оси аппликат на угол
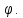
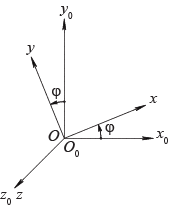
При этом положительное направление отсчета угла
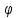
‑ направление, противоположное направлению хода часовой стрелки, если смотреть со стороны положительного направления оси аппликат.
Матрица этого преобразования:
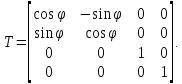
Иногда решается обратная задача: известны координаты точки в системе
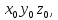
требуется определить координаты этой точки в системе
которая определенным образом переместилась относительно системы
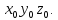
Данная задача решается при помощи обратного преобразования координат. Если необходимо осуществить обратное преобразование, т. е. перейти от системы координат
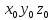
к системе координат
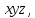
то применяют соответствующие каждому рассмотренному ранее виду составляющего движения обратные матрицы:
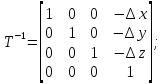
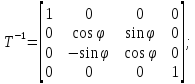
Любая обратная матрица обладает следующим свойством:
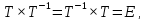
где
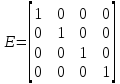
‑ это т. н. единичная матрица.
Единичная матрица также обладает особым свойством:
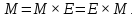
2.8. Определение огибающей при прямолинейно-поступательном движении поверхности
Рассмотрим прямолинейно-поступательное движение конической поверхности со скоростью
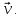
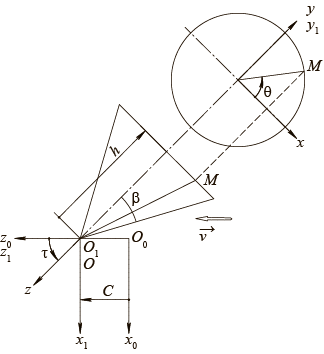
Введем следующие системы координат:
1) неподвижную систему
2) систему
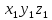
с началом отсчета в вершине конуса, связанную с конической поверхностью, ось
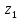
которой совпадает с осью
а остальные осипараллельны соответствующим осям системы
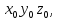
движуюся вдоль положительного направления оси
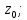
3) систему
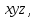
с началом отсчета в вершине конуса, связанную с конической поверхностью, которая получается из системы
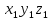
поворотом относительно оси
на угол
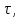
причем ось
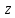
является осью конуса и направлена в сторону, противоположную основанию.
В системе координат
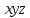
координаты любой точки
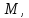
лежащей на поверхности конуса, определяются следующим образом:
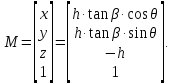
Координаты этой точки в системе координат
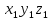
можно найти при помощи следующего преобразования:
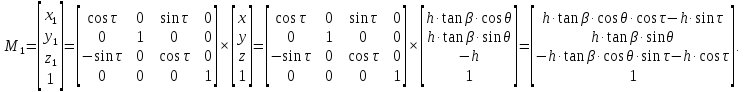
Координатыточки в системекоординат
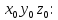
Определяемчастныепроизводные:
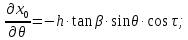
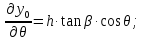
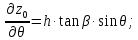
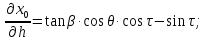
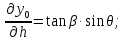
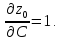
Составляемопределитель:
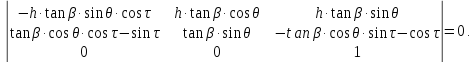
После преобразования получаем:
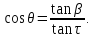
Это соотношение определяет положение характеристики на поверхности конуса. Следовательно, уравнение огибающей поверхности определяется системой уравнений:
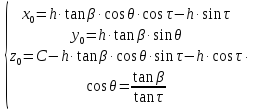
Из этих уравнений следует, что координата
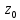
может принимать любое значение, а координаты
связаны зависимостью
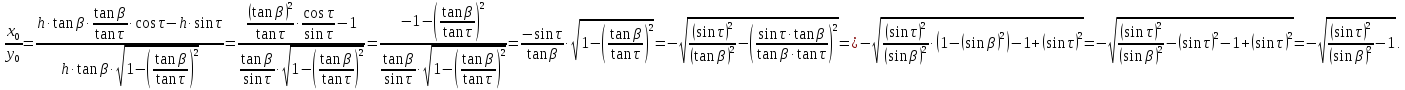
Таким образом, это отношение является постоянной величиной. Следовательно, огибающая поверхность в рассматриваемом случае будет плоскостью, которая идет параллельно оси
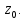
Угол между этой плоскостью и осью
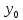
находят следующим образом:
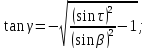
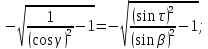
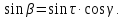
Подобная задача решается при анализе способов заточки сверл малых диаметров двумя шлифовальными кругами, установленными на одной оси.
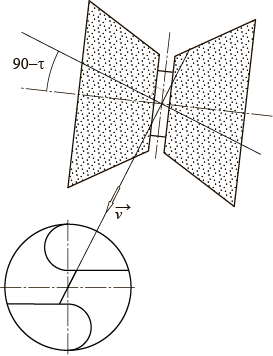
При заточке шлифовальные круги, как обычно, вращаются вокруг своей оси. Затачиваемое сверло совершает возвратно-поступательное движение под углом к оси кругов. В этом случае шлифовальные круги обрабатывают две пересекающиеся плоскости. С этими плоскостями совмещают при установке затачиваемые задние плоскости сверла.
Требуемый угол
зависит от углов
Если
то
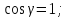
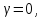
т. е. профиль огибающей вырождается в точку с координатами
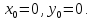
Таким образом, существуют такие сочетания указанных углов, при которых огибающая не существует.