
- •1. Элементы дифференциальной геометрии
- •1.1. Векторные функции скалярного аргумента
- •1.2. Понятие кривой
- •1.3. Кривизна кривой
- •1.4. Понятие поверхности
- •1.5. Квадратичные формырегулярнойповерхности
- •1.6. Нормальная кривизна регулярнойповерхности
- •2. Формообразование поверхностей резанием
- •2.1. Исходная инструментальная поверхность
- •2.2. Способы образования исходных инструментальных поверхностей
- •2.3. Аналитический способ определения огибающей семейства плоских кривых
- •2.4. Аналитический способ определения огибающей семейства поверхностей
- •2.5. Кинематический способ определения огибающих семейства плоских кривых и семейства поверхностей
- •2.6. Способ профильных нормалей
- •2.7. Преобразования координат
- •2.8. Определение огибающей при прямолинейно-поступательном движении поверхности
- •2.9. Определение огибающей при винтовом движении поверхности
- •2.10. Формообразование прямолинейного профиля шлицев шлицевого вала
- •2.10.1. Геометрические параметры шлицевого вала с прямолинейным профилем шлицев
- •2.10.2.Формообразование прямолинейного профиля шлицев шлицевого вала червячной фрезой
- •2.10.3.Формообразование прямолинейного профиля шлицев шлицевого вала долбяком
- •2.11. Формообразование эвольвентного профиля
- •2.11.1.Геометрические параметры эвольвенты
- •2.11.2.Геометрические параметры цилиндрическогоэвольвентногоколеса с внешними зубьями
- •2.11.3.Формообразованиеэвольвентногопрофиля рейкой
- •2.11.4. Формообразованиеэвольвентного профиля долбяком
- •2.11.5. Интерференция цилиндрических эвольвентных колес внешнего зацепления
- •2.12. Формообразование винтовых поверхностей дисковыми и пальцевыми фрезами
- •3. Условия формообразования поверхностей резанием
- •3.1. Условие существования исходной инструментальной поверхности
- •3.2. Условие соприкосновения исходной инструментальной поверхности с поверхностью детали без внедрения
1. Элементы дифференциальной геометрии
1.1. Векторные функции скалярного аргумента
Векторназывается векторной функцией скалярного аргумента, если каждому значению скаляра из области допустимых значений соответствует определенное значение вектора:

Вектор
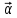
называется бесконечно малым, если его модуль стремится к нулю.
Производной векторной функции по ее скалярномуаргументуназывается предел отношения приращения вектора к соответствующему приращению аргумента, когда это приращение стремится к нулю:
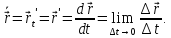
Некоторые правила дифференцирования векторной функции по скалярному аргументу:
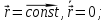
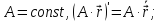
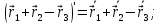
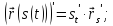
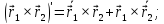
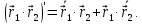
Докажем справедливость последнего правила.
Пусть
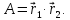
Если скалярному аргументу
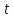
дать приращение
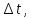
то векторные функции
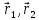
получат приращения
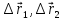
соответственно. При этом
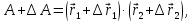
откуда
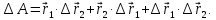
Поделим обе части этого равенства на
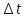
и перейдем к пределу при
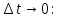
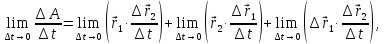
откуда и следует, что доказываемое правило справедливо.
Применительно к векторной функции скалярного аргумента рассматриваются также дифференциал
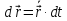
и интегралы, в частности определенный интеграл
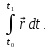
Если векторную функцию скалярного аргумента рассматривать в декартовой системе координат, то
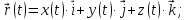
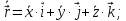
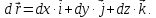
1.2. Понятие кривой
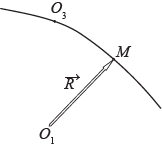
Кривую опишем при помощирадиус-вектора
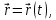
соединяющего произвольный фиксированный центр и точку, принадлежащую кривой.
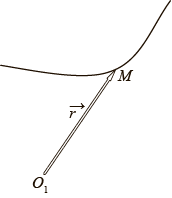
Кривая задается на промежутке
некоторой числовой оси.
Кривая называется регулярной, если во всех точках заданного промежутка
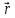
непрерывно дифференцируема и
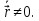
Пусть
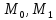
‑точки, принадлежащиерегулярнойкривой и соответствующие параметрам
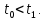
Прямая
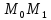
называется направленной секущей кривой в точке
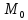
Направленной касательной к кривойвточке
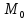
называется предел направленных секущих в этой точкепри
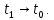
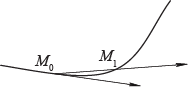
Теорема: в каждойточке регулярной кривой существует направленная касательная, определяемая направляющим вектором
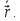
Доказательство.
Вектор
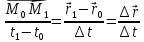
лежит на направленной секущей, проходящей через точки

которым соответствуют радиус-векторы
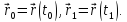
Производная

Отсюда следует, что в точке
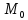
существует направленная касательная к кривой, которая определяется в пространстве вектором

Теорема доказана.
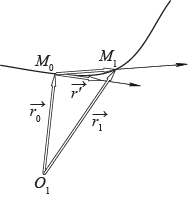
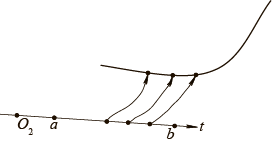
Длиной регулярной кривой называется предел длины ломаной, вписанной в кривую, при стремлении к нулю длины наибольшего сегмента ломаной.

Теорема: всякая регулярная кривая имеет определенную длину. Более того, если регулярная кривая задана векторной функцией
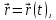
тодлинакривой
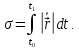
Доказательство.
Впишем в кривую ломаную. Длина этой ломаной

где
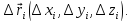
При этом
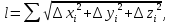
Согласно теореме Лагранжа имеем
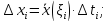
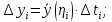
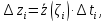
где
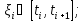
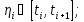
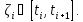
Отсюда
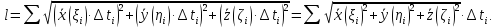
Перейдя к пределу, получим:
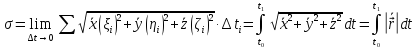
Теорема доказана.
Следствие из теоремы:
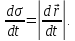
Введем такой скалярный аргумент радиус-вектора
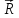
точкирегулярнойкривой, как длина дуги
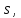
отсчитываемая от некоторого центра, взятого на кривой.
Данный аргументназывается естественным.
Теорема: имеет место соотношение:
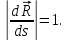
Доказательство.
Имеем:
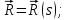
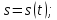

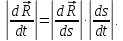
Учитывая, что
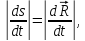
получаем
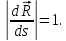
Теорема доказана.
1.3. Кривизна кривой
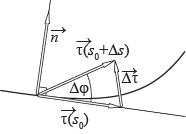
На регулярной кривой возьмем две точки, радиус-векторы которых обозначим
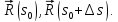
Единичные векторынаправленных касательных к траектории в указанныхточках обозначим
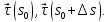
соответственно.Угол
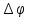
между векторами
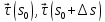
называется углом смежности траектории в точке, задаваемой радиус-вектором
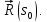
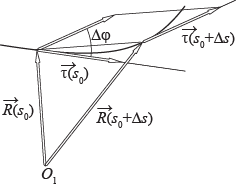
Число
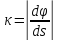
называется кривизной. Кривизна прямойравна 0.
Радиусом кривизны называется величина, обратная кривизне:
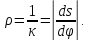
Радиус кривизны окружности во всех ее точках равен радиусу окружности.
Теорема: в каждой своей точке регулярная кривая характеризуется кривизной и для всех значений естественногопараметрасправедлива т. н. первая формула Френе, т. е.
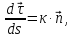
где
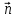
‑ это единичный вектор, называемый главной нормалью, причем
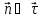
и
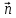
направлен в сторону вогнутости плоской кривой.
Доказательство.
Сначала докажем, что векторы
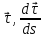
ортогональны:
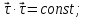

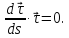
Отсюда следует, что орт вектора
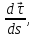
обозначаемый
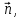
есть вектор, перпендикулярный вектору
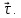
Далее докажем, что
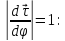
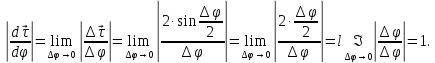
При этом
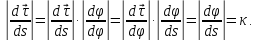
Вектор
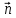
является предельным положением вектора
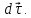
Если кривая плоская, то вектор
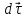
направлен в сторону вогнутости этой кривой, следовательно, и вектор
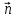
также направлен в сторону вогнутости этой кривой.
Теорема доказана.
Следствие из теоремы:
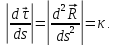
Плоскость, проходящая через векторы
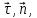
называется соприкасающейся.Соприкасающаяся плоскость является предельным положением плоскости, проходящей через векторы
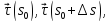
приложенные в точке, задаваемой радиус-вектором

Во всех точках плоскойрегулярнойкривойопределенаодна и та же соприкасающаяся плоскость, совпадающая с плоскостью самой кривой.
Теорема: для регулярной кривой справедлива формула:
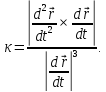
Доказательство.
Имеем:
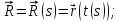
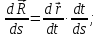
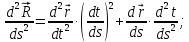
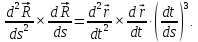
Поскольку векторы
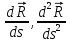
ортогональны и
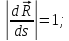
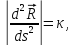
то
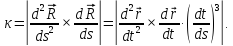
Но
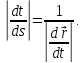
Следовательно
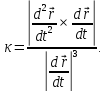
Теорема доказана.
В случае, если рассматривается плоская регулярная кривая
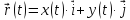
в плоскости
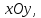
то
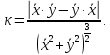
В случае,если
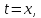
т. е.
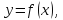
то
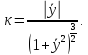
Если уравнение плоской регулярной кривой задано в полярных координатах, то

