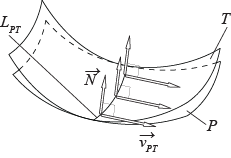
- •1. Элементы дифференциальной геометрии
- •1.1. Векторные функции скалярного аргумента
- •1.2. Понятие кривой
- •1.3. Кривизна кривой
- •1.4. Понятие поверхности
- •1.5. Квадратичные формырегулярнойповерхности
- •1.6. Нормальная кривизна регулярнойповерхности
- •2. Формообразование поверхностей резанием
- •2.1. Исходная инструментальная поверхность
- •2.2. Способы образования исходных инструментальных поверхностей
- •2.3. Аналитический способ определения огибающей семейства плоских кривых
- •2.4. Аналитический способ определения огибающей семейства поверхностей
- •2.5. Кинематический способ определения огибающих семейства плоских кривых и семейства поверхностей
- •2.6. Способ профильных нормалей
- •2.7. Преобразования координат
- •2.8. Определение огибающей при прямолинейно-поступательном движении поверхности
- •2.9. Определение огибающей при винтовом движении поверхности
- •2.10. Формообразование прямолинейного профиля шлицев шлицевого вала
- •2.10.1. Геометрические параметры шлицевого вала с прямолинейным профилем шлицев
- •2.10.2.Формообразование прямолинейного профиля шлицев шлицевого вала червячной фрезой
- •2.10.3.Формообразование прямолинейного профиля шлицев шлицевого вала долбяком
- •2.11. Формообразование эвольвентного профиля
- •2.11.1.Геометрические параметры эвольвенты
- •2.11.2.Геометрические параметры цилиндрическогоэвольвентногоколеса с внешними зубьями
- •2.11.3.Формообразованиеэвольвентногопрофиля рейкой
- •2.11.4. Формообразованиеэвольвентного профиля долбяком
- •2.11.5. Интерференция цилиндрических эвольвентных колес внешнего зацепления
- •2.12. Формообразование винтовых поверхностей дисковыми и пальцевыми фрезами
- •3. Условия формообразования поверхностей резанием
- •3.1. Условие существования исходной инструментальной поверхности
- •3.2. Условие соприкосновения исходной инструментальной поверхности с поверхностью детали без внедрения
2.3. Аналитический способ определения огибающей семейства плоских кривых
Регулярная кривая называется огибающей семейства плоских кривых, если она в каждой своей точке касается хотя бы одной кривой семейства и каждым своим отрезком касается бесконечного количества кривых семейства.
Теорема: пусть регулярные кривые семейства заданы уравнением
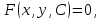
тогда огибающая этого семейства задается уравнениями
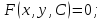
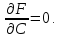
Доказательство.
Рассмотрим скалярное произведение касательногоинормальноговектороввнекоторой точке огибаемой кривой:
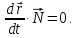
Причем

определяется координатами

где
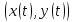
‑это координаты вектора
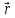
точкиогибаемойкривой.
Имеем
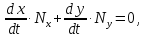
где
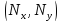
‑это координаты нормального вектора к огибаемой кривой.
Уравнение огибаемой кривой
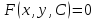
представим в следующем виде:

Дифференцируемэтоуравнение:

Сравнивая полученное выражение со скалярным произведением

приходим к выводу, что
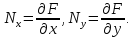
Имеет место уравнение
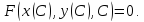
Дифференцируемэтоуравнение:
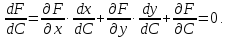
Координаты
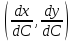
‑ это координаты касательного вектора к огибающей, коллинеарного касательному вектору к огибаемой кривой, а
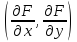
‑ это координаты нормальноговекторакогибаемой кривой, поэтому
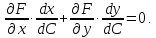
Принимая во внимание, что
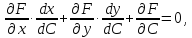
получаем
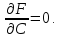
Теорема доказана.
Теорема: пусть регулярные кривые семейства заданы уравнениями

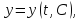
тогда огибающая этого семейства задается уравнениями
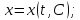

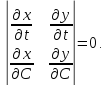
Доказательство.
Векторное уравнение огибаемой кривой:

Также имеет место векторное уравнение:
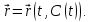
Вектор, касательный к огибаемой кривой:
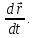
Вектор, касательный к огибающей:

Т. к. эти векторы коллинеарны, то

откуда следует, что
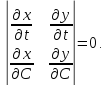
Теорема доказана.
Огибающая и огибаемая кривые в точке касания не всегда имеют общую касательную.

2.4. Аналитический способ определения огибающей семейства поверхностей
Теорема: пусть регулярные поверхности семейства заданы уравнением
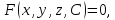
тогда огибающая этого семейства задается уравнениями
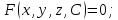
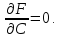
Теорема: пусть регулярные поверхности семейства заданы уравнениями

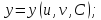
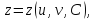
тогда огибающая этого семейства задается уравнениями

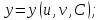
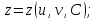
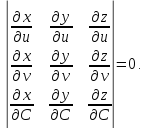
Семейство регулярных поверхностей может быть двухпараметрическим:
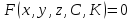
или
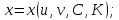
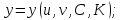
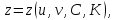
тогда огибающая определяется дополнительно уравнениями
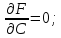
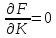
или
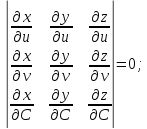
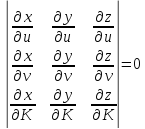
соответственно.
2.5. Кинематический способ определения огибающих семейства плоских кривых и семейства поверхностей
Пусть в системе координат
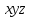
задана поверхность детали
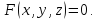
Эта поверхность совершает некоторое движение в системе координат
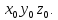
Будем считать, что положение системы

относительно системы
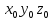
определяется одним параметром
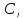
тогда в системе координат
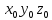
семейство поверхностей детали опишется уравнением
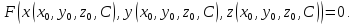
Дифференцируемэтоуравнение:
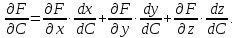
На примере плоских кривых ранее было показано, что вектор, нормальный к поверхности детали в системе координат
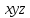
может быть найден следующим образом:
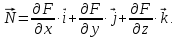
Вектор относительной скорости в системе координат

определяется следующим образом:
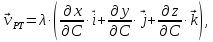
где
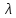
‑ это коэффициент.
Частные производные
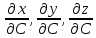
могут быть найдены из формул преобразования системы координат
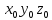
в систему координат

Учитывая, что
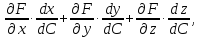
получаем
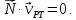
Данный вывод справедлив и для регулярной плоской кривой, движущейся в ее плоскости. Например, если такая кривая лежит в плоскости

то она является профилем цилиндрической поверхности. Если для этой поверхности выполняется условие

то, очевидно, это условие выполняется и для указанной кривой.
Уравнение
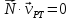
называется уравнением контакта и означает, что в точках контакта сопряженных поверхностей общий нормальный вектор перпендикулярен к скорости относительного движения.
Поверхность
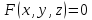
в общем случае может совершать сложное движение. В этом случае скорость точки этой поверхности определяется как сумма скоростей составляющих движений:
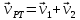
и уравнение контакта принимает вид
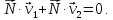
В одном из составляющих движений поверхность может скользить «сама по себе», тогда это движение не учитывается. Например, если поверхность «скользит сама по себе» со скоростью
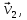
то
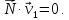
Итак, если известная поверхность детали движется и образует огибающую поверхность – исходную инструментальную поверхность, то характеристику можно определить как линию, в каждой точке которой вектор относительной скорости направлен по касательной к поверхности детали. Взятые в определенные моменты времени точки контакта определяют характеристику. Совокупность характеристик, определенных в различные моменты времени, в системе координат инструмента дает исходную инструментальную поверхность, а совокупность характеристик в системе координат детали дает поверхность детали.