Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

0887579_C36AB_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat

.pdf

Скачиваний:

Добавлен:

19.02.2016

Размер:

3.59 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 4513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

		β	ρ(ϕ)	f (ρ cos ϕ, ρ sin ϕ) ρdρ.
	∫∫ f ( x, y)dxdy = ∫ dϕ ∫			f (ρ cos ϕ, ρ sin ϕ) ρdρ.	(2.8)
	D	α	0
2. Нехай область D обмежена променями, які утворюють з полярною
віссю кути	α та	β (α < β), і кривими		ρ = ρ1 (ϕ) та ρ = ρ2 (ϕ)	(ρ1 ≤ ρ2 )
(рис. 2.11,	б). Тоді полярні координати області D1 змінюються в межах
ρ1 (ϕ) ≤ ρ ≤ ρ2 (ϕ),		α ≤ ϕ ≤ β і формулу (2.7) можна записати у вигляді
		β	ρ 2 (ϕ)
	∫∫ f ( x, y)dxdy = ∫ dϕ		∫	f (ρ cos ϕ, ρ sin ϕ) ρdρ.	(2.9)
	D	α	ρ1 (ϕ)

3. Нехай область D, межа якої задана полярним рівнянням ρ = ρ(ϕ) , охоплює початок координат, тобто точка O(0; 0) є внутрішньою точкою області D (рис. 2.11, в), тоді виконується формула

				2π	ρ(ϕ)
			∫∫ f ( x, y)dxdy = ∫ dϕ ∫ f (ρ cos ϕ, ρ sin ϕ) ρdρ .								(2.10)
			D	0	0
Зокрема, якщо межа області D — коло x2 + y2 = R2 , або											ρ = R , тоді
формула (2.10) набуває найпростішого вигляду
				2π	R
			∫∫ f (x, y) dxdy = ∫ dϕ∫ f (ρ cos ϕ, ρ sin ϕ) ρdρ .
			D	0	0
y				y						y
			ρ = ρ(φ)	y

							ρ = ρ2(φ)
							ρ = ρ2(φ)
						D
		D				D					ρ = ρ(φ)
											ρ = ρ(φ)
	α β				α β ρ = ρ1(φ)				D		x
										О
										О
О			x	О			x
а				б				в
					Рис. 2.11
Зауваження.
1. Оскільки в полярних координатах вираз x2 + y2								має досить простий
вигляд	x2 + y2 = ρ2 , а рівняння кола x2 + y2 = R2 ––							ρ = R , то до поляр-

них координат найчастіше переходять тоді, коли область D ― круг, кільце,

121

сектор тощо, при цьому підінтегральна функція часто має вигляд f (x, y) = g(x2 + y2 ) .

Y			2. У деяких випадках, наприклад, коли область
		M	D обмежена колом (x − x0 )	2	+ ( y − y0 )	2	= R	2	, до-
у	ρ
		p
M0	φ		цільно перейти до полярних координат із полюсом
y0			у точці M0 (x0 , y0 ) і полярною віссю, напрям якої
О x0	х	Х	збігається з додатним напрямом осі абсцис. У цьому
			разі перехід від прямокутних декартових координат
Рис. 2.12			(x, y) до полярних координат		(ρ, ϕ) (рис. 2.12) здій-
			снюєтьсязаформулами x − x0 = ρcos ϕ , y − y0 = ρsin ϕ ,

прицьомуякобіанзалишаєтьсянезмінним: J = ρ.

1.6.Деякі застосування подвійного інтеграла

1.Площу S плоскої області D обчислюють за формулою

	S = ∫∫ dxdy.	(2.11)
	D

У полярних координатах ця формула має вигляд
	S = ∫∫ ρdρdϕ .
	D1

2. Об’єм циліндричного тіла, обмеженого зверху неперервною поверхнею z = f (x, y) , де f (x, y) ≥ 0 , знизу — замкненою обмеженою областю

D, з боків — циліндричною поверхнею, напрямна якої збігається з межею області D, а твірні паралельні осі Oz, визначають за формулою

V = ∫∫ f (x, y)dxdy.	(2.12)
D

3. Площу Sσ гладкої поверхні σ , заданої рівнянням z = f (x, y) , обчислюють за формулою

Sσ = ∫∫ 1+ ( fx′(x, y))2 + ( fy′ (x, y))2 dxdy,

(2.13)

Dxy

де Dxy ― проекція поверхні на площину Оху.

122

4. Масу m плоскої пластини, яка має форму обмеженої замкненої області

D, в кожній точці якої задано густину γ(x,					y) , обчислюють за формулою

				m = ∫∫ γ(x, y)dxdy.				(2.14)
				D
5. Координати xc ,			yc центра маси пластини визначають за формулами

	xc =	1	∫∫ xγ(x,	y)dxdy, yc	=	1	∫∫ yγ(x, y)dxdy.	(2.15)
	xc =	m	∫∫ xγ(x,	y)dxdy, yc	=	m	∫∫ yγ(x, y)dxdy.	(2.15)
			D				D
Зауваження. Величини
	M y = ∫∫ xγ(x,			y)dxdy, M x	= ∫∫ yγ(x, y)dxdy
			D			D

називаються статичними моментами пластини відносно осей Оу та Ох

відповідно. Тоді координати центра маси пластини можна записати у ви- г-ляді

x	=	M y	,	y	=	M	x	.

c		m		c		m

6. Моменти інерції пластини відносно координатних осей обчислюють за формулами

			Ix = ∫∫ y2 γ(x,		y)dxdy,	I y = ∫∫ x2 γ(x, y)dxdy,
			D			D

а відносно початку координат ― за формулою

				I0 = ∫∫ (x2 + y2 )γ(x, y)dxdy.
				D

	Т.1	ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
1. У подвійному інтегралі					∫∫ f (x,	y)dxdy розставте межі інтегрування
					D

(двома способами) по області D, межа якої задана такими рівняннями:

а) x = 1 , x = 4, y = 1, y = 3 ;

б) y = x − 1, x = 3 , y = −1 ;

в) y = 2x, x + y = 3, y = 0 ;

123

О 1 4 x

Рис. 2.13

y
2	у = х – 1
	1
О	3 x
	у = – 1

Рис. 2.14

г) y = 2x − 2, y = 2x − 8, y = 0 , y = 2 ; д) y = x , y = x − 2 , x = 0 ;

е) y = 0 , y = 3 , x = 0 , x = 2 , x = 2 y − y2 .

Розв’язання: а) Маємо найпростіший випадок. Область інтегрування ― прямокутник, зображений на рис. 2.13. Ця область правильна і в напрямку осі Ох, і в напрямку осі Оу. Проекція області на вісь Ох ― відрізок [1; 4] , а на вісь Оу ― відрізок

[1; 3] . Оскільки сторони прямокутника паралельні

осям координат, то подвійний інтеграл зводиться до повторного інтеграла за формулами

∫∫ f (x,	4	3
∫∫ f (x,	y)dxdy = ∫ dx∫ f (x,		y)dy
D	1	1
або	3	4
∫∫ f (x,	3	4
∫∫ f (x,	y)dxdy = ∫ dy∫ f (x,		y)dx .
D	1	1

б) Область інтегрування –– трикутник (рис. 2.14). Ця область є правильною. Як і в попередньому випадку розбивати область інтегрування на частини не потрібно. Далі міркуємо так. Область інтегрування лежить між

прямими x = 0 та	x = 3, її нижня межа		y = −1 , а верхня –– y = x − 1 , тому
за формулою (2.4)	маємо
		3	x−1
	∫∫ f (x, y)dxdy = ∫ dx ∫ f (x, y)dy .
	D	0	−1

Спроектуємо тепер область D на вісь Оу. У результаті дістанемо відрізок [−1; 2] . Область D розміщена між прямими y = −1 та y = 2 , причому

ліва межа має рівняння x = y + 1, а права ––			x = 3 . Отже, якщо −1 ≤ y ≤ 2 ,
то y + 1 ≤ x ≤ 3 , тому
	3	3
∫∫ f (x, y)dxdy = ∫ dy ∫			f (x, y)dx .
D	−1	y+1

в) Область інтегрування –– трикутник (рис. 2.15). Ця область також правильна в обох напрямах, але на відміну від попередніх випадків існує суттєва відмінність. Спроектуємо область D на вісь Ох, дістанемо відрізок [0; 3] , точка перетину прямих y = 2x та y = 3 − x проектується у точку,

абсциса якої x = 1 . Нижня межа області D на всьому проміжку [0; 3]

124

задається одним рівнянням y = 0 , тоді як верхня межа складається з двох частин, їхні рівняння: y = 2x , якщо x [0; 1] , та y = 3 − x , якщо x [1; 3]

(рис. 2.15, а). Як наслідок, щоб звести подвійний інтеграл до повторного, де внутрішнє інтегрування відбувається за змінною y , область інтегру-

вання потрібно розбити на дві частини: якщо 0 ≤ x ≤ 1, то 0 ≤ y ≤ 2x ; якщо 1 ≤ x ≤ 3 , то 0 ≤ y ≤ 3 − x , тому

∫∫ f (x,				1	2x	3	3− x
∫∫ f (x,			y)dxdy = ∫ dx ∫ f (x,			y)dy + ∫ dx ∫ f (x,		y)dy.
D				0	0	1	0
y						y
3			y = 2x			3
3		А				3	А
2			y = 3 – x			2



			В					В
О	1		3	x		О	1	3 x
а						б
					Рис. 2.15

Розставимо межі інтегрування іншим способом. Для цього спроектуємо область D на вісь Оу. У результаті дістанемо відрізок [0; 2] . Область D

розміщена між прямими y = 0 та y = 2 , як видно з рис. 2.15, б, у цьому випадку розбивати область D на окремі частини вже не потрібно. Якщо

0 ≤ y ≤ 2 , то	y	≤ x ≤ 3 − x . Отже,
0 ≤ y ≤ 2 , то	2	≤ x ≤ 3 − x . Отже,
	2
		∫∫ f (x,	2	3− y
		∫∫ f (x,	y)dxdy = ∫ dy ∫ f (x, y)dx .
		D	0		y
				2

г) Область інтегрування –– паралелограм (рис. 2.16, а), розміщений у

смузі між прямими y = 0 та y = 2 і обмежений зліва прямою x =							y	+ 1 (тут
							2	+ 1 (тут
					y		2
х виражений через у з рівняння y = 2x − 2 ) та x =					y	+ 4 , тому
х виражений через у з рівняння y = 2x − 2 ) та x =					2	+ 4 , тому
		y			2
		y	+ 4
∫∫ f (x,	2	2∫ f (x,
∫∫ f (x,	y)dxdy = ∫ dy	2∫ f (x,			y)dx .
D	0	y		+1
D	0	2		+1
		2
								125

Для того, щоб розставити межі в іншому порядку, розбиваємо область D на три частини (див. рис. 2.16, б):

D1 : 1 ≤ x ≤ 2 , 0 ≤ y ≤ 2x − 2 ; D2 : 2 ≤ x ≤ 4 , 0 ≤ y ≤ 2 ;

D3 : 4 ≤ x ≤ 5 , 2x − 8 ≤ y ≤ 2 .

Межі інтегрування розставляємо так:

2x−2

∫∫ f (x, y)dxdy = ∫ dx

∫

f (x,

y)dy + ∫ dx∫ f (x, y)dy + ∫ dx ∫

f (x, y)dy.

2x−8

О 1

4 5

О 1 2

4 5 x

Рис. 2.16

д) Область інтегрування обмежена верхньою

y =

віткою параболи y2 = x ,

прямими

x = 0

та

y = x − 2 (рис. 2.17). Область D розміщена у

смузі між прямими x = 0

та

x = 4 ,

рівняння

нижньої межі

y = x − 2 , а верхньої ––

y =

x .

–2

y = x – 2

Тому

∫∫ f (x,

Рис. 2.17

y)dxdy = ∫ dx ∫

f (x,

y)dy .

x−2

Проекція області D на вісь Оу –– відрізок [−2; 2] . Ліва межа області D

складається з двох частин –– відрізка та дуги параболи. Тому область інтегрування розбиваємо на дві частини:

D1 : −2 ≤ y ≤ 0 , 0 ≤ x ≤ 2 + y ;
D : 0 ≤ y ≤ 2 , y2 ≤ x ≤ 2 + y .
2
У результаті маємо
∫∫ f (x,	0	y+ 2	2	y+ 2
∫∫ f (x,	y)dxdy = ∫ dy ∫ f (x,		y)dx + ∫ dy ∫ f (x, y)dx.
D	−2	0	0	y2

126

е) Область інтегрування (див. 2.18, а), обмежена прямими y = 0 , y = 3 ,


x = 0 ,	x = 2	та правою частиною	кола	x2 + ( y − 1)2 = 1		(рівняння
x = 2 y − y2		рівносильне рівнянню x2	= 2 y − y2 , або		x2 + ( y2 − 2 y + 1) = 1
за умови x ≥ 0 ). З рівняння кола визначаємо				y = 1±	1− x2 , причому рів-
няння	y = 1+	1− x2 визначає верхнє півколо, а рівняння y = 1−				1− x2 ––

нижнє півколо. У напрямку осі ординат область D не є правильною, тому розбиваємо її на три правильні області, а саме (див. рис. 2.18, б):

			D : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1− 1− x2 ;
			1
			D : 0 ≤ x ≤ 1, 1+ 1− x2				≤ y ≤ 3;
			2
Тоді			D3 : 1 ≤ x ≤ 2 , 0 ≤ y ≤ 3.
Тоді
∫∫ f (x,	1	1− 1− x2		1		3	2	3
∫∫ f (x,	y)dxdy = ∫ dx		∫	f (x, y)dy + ∫ dx		∫	f (x, y)dy + ∫ dx∫ f (x, y)dy.
D	0		0	0	1+ 1− x2		1	0

Для того, щоб розставити межі в іншому порядку, розбиваємо область D на дві частини прямою y = 2 (див. рис. 2.18, в):

D : 0 ≤ y ≤ 2 , 0 ≤ x ≤ 2 y − y2 ;

D2 : 2 ≤ y ≤ 3 , 0 ≤ x ≤ 2 .

Тоді

2 y− y2

∫∫ f (x, y)dxdy = ∫ dy ∫ f (x,

y)dx + ∫ dy∫ f (x,

y)dx.

О 1 2

1 2

О 1 2

Рис. 2.18

127

2. Змініть порядок інтегрування у подвійному інтегралі та накресліть область інтегрування.

y = 5 – x2

D	х = 2у

О2 x

Рис. 2.19

2 5− x2

∫ dx ∫ f (x, y)dy .

Розв’язання. З вигляду меж інтегрування випливає, що область інтегрування розміщена у смузі між прямими x = 0 та x = 2 , знизу область D обмежена

прямою y = 2x , а зверху –– правою віткою параболи

y = 5 − x2 . Побудувавши графіки цих рівнянь,

дістанемо область D (див. рис. 2.19).

Для зміни порядку інтегрування спроектуємо область D на вісь Оy, дістанемо відрізок [0; 5] . Оскільки права

межа області складається з двох різних ліній, то цю область розбиваємо на дві частини прямою y = 1 , на якій

лежить точка перетину цих ліній. Виразивши з рівнянь							y =	x	та y = 5 − x2
лежить точка перетину цих ліній. Виразивши з рівнянь							y =		та y = 5 − x2
зміннухчерезу, урезультатідістанемо							2
зміннухчерезу, урезультатідістанемо
2	5− x2		1	2 y	5	5− y
∫ dx ∫ f (x, y)dy = ∫ dy ∫ f (x, y)dx + ∫ dy ∫ f (x, y)dx.
0		x	0	0	1	0
	2

Зауваження. Зверніть увагу на те, що якщо у повторному інтегралі внутрішнє інтегрування проводиться за деякою змінною, то ця змінна як у нижній так і у верхній межах внутрішнього інтеграла не фігурує.

3. Обчисліть подвійний інтеграл

I = ∫∫ (x + 2 y)dxdy,

якщо область D обмежена прямою y = 2 − x та параболою y = x2 .

Розв’язання. Побудувавши графіки заданих рівнянь, дістанемо область інтегрування D (див. рис. 2.20). Ця область правильна як у напрямку осі ординат, так і в напрямку осі абсцис. Тому інтегрування можна проводити як за формулою (2.4), так і за формулою (2.5). На наш погляд, інтегрування зручніше проводити за формулою (2.4). Знайдемо абсциси точок перетину

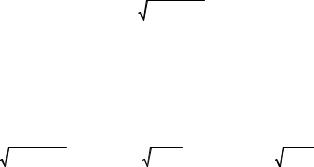
параболи з прямою: x2 = 2 − x , x2 + x − 2 = 0 , x = −2 ,	x = 1. Тоді
1	2
128

2− x

I = ∫∫ (x + 2 y)dxdy = ∫ dx ∫

(x + 2 y)dy = ∫ dx(xy + y2 )

−2

(4 − 2x − x3 − x4 )dx =

= ∫

(x(2 − x) + (2 − x)2 − x3 − x4 )dx = ∫

−2

− x2

−

= 4 −

1−

−

−8 − 4 − 4 +

= 12,15.

−2

4 5

4.Обчисліть подвійний інтеграл

∫∫1− x2 − y2 dxdy ,

якщо область D обмежена колом x2 + y2 = 1 .

Розв’язання. Область інтегрування D ― круг радіуса R = 1 з центром у початку координат (рис. 2.21). У полярних координатах рівняння кола ― межі області D ― має вигляд ρ = 1 . Враховуючи форму області D, подвійний

інтеграл обчислюватимемо в полярній системі координат (див. рис. 2.10).

		2π	1							1	2π	1
∫∫ 1− x2 − y2 dxdy = ∫			dϕ∫ 1− ρ2 ρdρ = −							1	∫ dϕ∫ 1− ρ2 d(1− ρ2 ) =
∫∫ 1− x2 − y2 dxdy = ∫			dϕ∫ 1− ρ2 ρdρ = −						2		∫ dϕ∫ 1− ρ2 d(1− ρ2 ) =
D		0	0						2		0	0
D		0	0								0	0
		2π	(1− ρ2 )		3	1		1 2π
	1	2π	(1− ρ2 )		2	1		1 2π				2π
= −		∫					dϕ =		∫		dϕ =		.
= −	2	∫		3		0	dϕ =	3	∫		dϕ =	3	.
	2	0		3				3	0			3
		0	2						0
			2

5. Обчислітьплощуобласті, обмеженоїлініями x2 + y2 = 4x, y = x, y = 0. Розв’язання. Зобразимо цю фігуру на рисунку. Рівняння x2 + y2 = 4x визначає коло радіуса два з центром у точці A(2; 0) . Справді, виділивши

повний квадрат за змінною x , дістанемо:

x2 − 4x + y2 = 0, (x2 − 4x + 4) + y2 = 4, (x − 2)2 + y2 = 4 .

Графіки рівнянь y = x та y = 0 –– прямі лінії, які разом із дугою кола

визначають область інтегрування D, яка являє собою криволінійний сектор з вершиною у початку координат (рис. 2.22).

Враховуючи форму області D, подвійний інтеграл обчислюватимемо в полярній системі координат.

129

y = x

ρ = 4cosφ

y = 2 – x

π/4

A(2; 0)

–2

Рис. 2.20

Рис. 2.21

Рис. 2.22

У полярних координатах рівняння кола має вигляд

ρ2 cos2 ϕ + ρ2 sin2 ϕ = 4ρ cos ρ,

ρ2 = 4ρ cos ρ,

ρ = 4 cos ϕ ,

прямі

y = 0 та

y = x

у полярних координатах набирають вигляду ϕ = 0 та

ϕ = π

відповідно. Отже,

полярні координати

ϕ і

ρ точок, які належать

області інтегрування, змінюються у межах: 0 ≤ ϕ ≤

, 0 ≤ ρ ≤ 4ρ cos ϕ .

За формулою (2.11) маємо

4cosϕ

S = ∫∫ dxdy = ∫∫

4cosϕ

ρdρdϕ = ∫ dϕ

∫

ρ dρ = ∫

dϕ =

π4

1+ cos 2ϕ

sin 2ϕ

= 8∫ cos

ϕd

ϕ = 8∫

dϕ = 4

ϕ +

= 4

= π + 2.

6. Використовуючи геометричний зміст подвійного інтеграла, обчисліть

об’ємтіла, обмеженогоповерхнями z = 4− 2y2 , z = 0,	x = 0, y = 0 та x+ 2y = 2.
Розв’язання. Задане тіло обмежене зверху	параболічним циліндром

z = 4 − 2 y2 , знизу ― координатною площиною Оху, з боків ― паралельними осі Оz площинами Охz, Оyz та x + 2 y = 2 . Отже, задано циліндричне тіло (рис. 2.23), об’єм якого обчислимо за формулою (2.12). Область

інтегрування D ― трикутник ОАВ: 0 ≤ y ≤ 1,			0 ≤ x ≤ 2 − 2 y . Використо-
вуючи формулу (2.5), дістанемо
	1	2−2 y	1	2−2 y

V = ∫∫ (4 − 2 y2 )dxdy = ∫ dy		∫ (4 − 2 y2 )dx =∫ (4 − 2 y2 )x		dy =
D	0	0	0	0
130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 4513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.08.20195.47 Mб21(Т4 укр)м(Л21).doc
#
29.08.20193.68 Mб36(Т5укр)м(Л22-23).doc
#
11.12.2018296.96 Кб12+Изгот микросхем.doc
#
11.12.2018437.76 Кб3+страничная память.doc
#
19.02.20162.32 Mб210887578_645D9_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat.pdf
#
19.02.20163.59 Mб510887579_C36AB_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat.pdf
#
19.09.2019106.5 Кб01 000 000 $.doc
#
16.11.20191.38 Mб11 Lab (Neuro).docx
#
19.02.20161.12 Mб1001 Конспект лекций Основы системного анализа.doc
#
25.11.2019238.27 Кб41 Літосферні стихійні лиха.docx
#
19.02.201652.22 Кб4741 ПЗ М1 Менеджмент.doc