
bmp
.pdf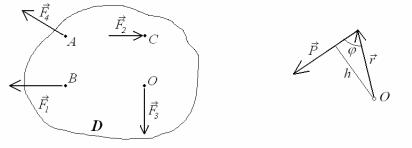
11
1.2. Довільна система сил
Плоскою довільною називається система сил, лінії дії яких належать одній площині і не перетинаються в одній точці (рис.1.12). Еквівалентними перетвореннями така система сил може бути
Рис. 1.12 Рис. 1.13
заміненою рівнодійною силою або парою сил – двома силами, які мають однакові модулі і діють в протилежних напрямках вздовж паралельних прямих. У практичних задачах довільну систему сил зводять до вибраного центра, визначивши головний вектор – геометричну суму всіх сил системи, лінія дії якого проходить через центр приведення, та головний момент – суму моментів усіх сил відносно центра приведення. Моментом сили P відносно точки (центра) О називається вектор, отриманий векторним множенням радіус-вектора r (від центра О до точки прикладання сили) на вектор сили P (рис. 1.13)
M0 P r P. |
(1.5) |
Згідно правил векторного добутку модуль M моменту сили відносно точки дорівнює добутку абсолютної величини сили P на відстань від точки О до лінії дії сили P .
M0 P P r sin P h |
(1.6) |
(величину h називають плечем сили P відносно точки О).
Вектор моменту перпендикулярний до площини, якій належать лінія дії сили P і точка О. Він направлений в той бік, звідки найкоротшим поворотом r до P здійснюється назустріч рухові стрілки годинника. Тому в плоских задачах момент M0 Pi вважатимемо додатнім, якщо тверде ті-
ло, уявно шарнірно закріплене в точці О, під дією сили P обертатиметься назустріч годинниковій стрілці.
Момент рівнодійної сили, згідно теореми Варіньона, відносно будь-якої точки дорівнює сумі моментів всіх сил системи відносно цієї точки.
Якщо, R n Pi , то
i 1
|
|
|
|
12 |
M0 R n |
M 0 Pi n |
Pi ri sin i n |
Pi hi . |
(1.7) |
i 1 |
i 1 |
i 1 |
|
|
Приведення плоскої довільної системи сил до вибраного центра О можна виконати графічно або аналітично.
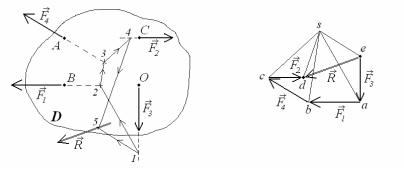
Графічне розв’язування полягає у визначенні вектора рівнодійної сили заданій системі сил та паралельного перенесення його до центра приведення. При цьому до тіла D потрібно прикласти момент, який рівнодійна утворювала відносно центра приведення до її перенесення. Рівнодійний вектор у загальному випадку можна побудувати послідовним геометричним додаванням усіх сил системи за правилом паралелограма. В часткових випадках, коли лінії дії сил паралельні, правило паралелограма не дозволяє визначити лінію дії сумарного вектора. Універсальним способом знаходження рівнодійної довільної системи сил на площині є побудова силового і мотузкового багатокутників. Силовий багатокутник (рис.1.14,б) – ланцюжок послідовно вишикуваних сил системи Fi (в прийнятому масштабі сил), замкнений рівнодійним вектором R , що поєднує першу точку цієї послідовності е з останньою – d. В околі силового багатокутника вибирається довільна точка
а |
б |
Рис. 1.14
– полюс s – яка поєднується відрізками (променями) з вершинами багатокутника. Мотузковий багатокутник створюють на кресленні диска, виконаному в певному масштабі (рис.1.14,а). Розпочинається побудова з вибору на лінії дії сили F3 , яка є першою ланкою силового багатокутника, до-
вільної точки 1. Через цю точку проводиться промінь, паралельний відрізку sа, що поєднує полюс s з кінцевою точкою першого вектора силового ланцюжка (рис.1.14,б). Точка 2 на перетині променя sa з лінією дії F1 – наступної (другої) сили у ланцюжку, є початком чергового променя, побу-
дованого паралельно прямій sb, що проходить через полюс і закінчення другої за раніше установленою послідовністю сили. Ці дії повторюються до визначення точки 4. Завершується побудова мотузкового багатокутника знаходженням точки 5 на перетині двох променів, проведених з першої (точки 1) та останньої (точки 4) точок паралельно відповідно se та sd у силовому багатокутнику. Ці промені спираються на вектор рівнодійної сили. Через відшукану точку 5 проходить лінія дії вектора рівнодійної сили (рис.1.14,а), напрямок якої і величина визначені в силовому багатоку-

13
тнику (рис.1.14,б). Для приведення системи сил до заданого центра О потрібно вектор рівнодійної сили перенести паралельно собі до точки О і при цьому, щоб не змінився механічний стан диску, доповнити головний вектор моментом, який рівнодійна сила створювала відносно вибраного центра до перенесення – головним моментом системи (рис.1.15,б). Модуль головного моменту можна порахувати, помноживши модуль головного вектора на плече – найкоротшу відстань від точки О до лінії дії рівнодійного вектора. Знак головного моменту визначається напрямком "обертання" вектора рівнодійної сили тіла D відносно "закріпленої" точки О.
а |
б |
Рис. 1.15
Аналітичне приведення довільної системи сил до заданого центра полягає у визначенні проекцій головного вектора на осі вибраної системи координат за формулами (1.1), його модуля (1.2) і направляючих кутів (1.3). Головний момент, згідно теореми Варіньона, дорівнює векторній сумі моментів всіх сил системи відносно точки О
M |
0 R n |
M |
0 Pi .. |
(1.5) |
|
i 1 |
|
|
|
У проекції на вісь, що перпендикулярна площині, в якій розв’язується задача,
M0 R n |
M0 Pi . . |
(1.6) |
i 1 |
|
|
Достовірність отриманих результатів підтверджується порівнянням величин проекцій і модуля головного вектора та його направляючих кутів, а також величини головного моменту, визначених аналітично і графічно. Критерієм точності є відносна похибка, яка обчислюється за формулою (1.4).
Приклад 2.
Дано: абсолютно тверде тіло D,
плоска довільна система сил F1 , F2 , F3 , F4 (рис.1.16).
F1 =10 кН, F2 =15 кН,
F3 =10 кН, F4 =20 кН.

14
Необхідно: привести задану систему сил до центра А.
Аналітичне розв’язування:
Вибираємо систему координат Oxy (рис.1.16). Проекції головного вектора на осі системи координат:
Rx 4 Fix F1x F2x F3x F4x
i1
F1 cos45 F2 cos0 F3 cos90 F4 cos150
10 0,7071 15 1 10 0 15 0,8660 9,08 кН;
Ry 4 |
Fiy F1y F2 y F3y F4 y |
i 1 |
|
F1 cos45 F2 cos90 F3 cos0 F4 cos3010 0,7071 15 0 10 1 15 0,5 24,57 кН.
Модуль головного вектора:
R 
 Rx2 Ry2
Rx2 Ry2 
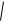 9,082 24,572 26,19кН.кН.
9,082 24,572 26,19кН.кН.
Напрямні кути:
arccos RRx arccos 26,199,08 arccos 0,3466 69,72 ;
arccos RRy arccos 24,5726,19 arccos 0,9380 20,28 .
Головний момент системи сил, приведеної до центру А
M A R 4 M A Fi
i1
F1 cos45 4 F1 cos45 0 F3 2 F2 0 F4 cos60 0 F4 cos30 2
10 0,7071 4 10 0,7071 0 10 2 15 0 20 0,8660 2 20 0,5 0
82,93кН.
15
Графічне розв’язування
Умова: |
Силовий багатокутник: |
:
Мотузковий багатокутник
Відповідь:
Рис.1.17
Порівняння результатів розв’язування двома способами виконується в таблиці 1.2:
Таблиця 1.2
Параметр |
Аналітичний |
Графічний |
Відносна |
|
|
|
спосіб |
спосіб |
похибка (%) |
Rx (кН) |
9,08 |
9,0 |
0,8 |
|
|
|
|
|
|
Ry (кН) |
24,57 |
24,5 |
0,3 |
|
|
|
|
|
|
R |
(кН) |
26,19 |
26,0 |
0,9 |
|
|
|
|
|
|
(град.) |
69,72 |
69,5 |
0,3 |
|
|
|
|
|
|
(град.) |
20,28 |
20,5 |
1,1 |
|
|
|
|
|
М |
( кНм) |
- 82,93 |
- 81,7 |
1,5 |
|
|
|
|
|

16
1.3. Задачі для самоконтролю
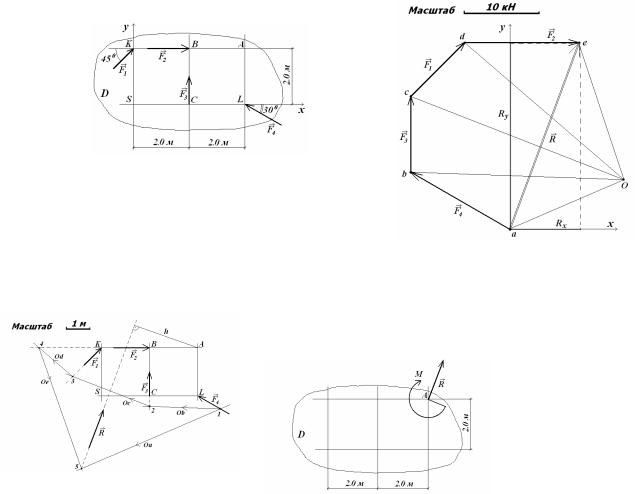
Привести систему сил (рис.1.18) до рівнодійної, якщо: F1 =20 кН, F2 =20 кН, F3 = 20 
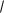 2 кН,
2 кН,
F4 =10 кН, F5 =30 кН.
Привести систему сил (рис.1.19) до центра О, якщо: F1 =20 кН, F2 =40 кН, F3 =20 
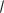 2 кН, F4 =30
2 кН, F4 =30
кН, F5 =15 кН.
2.Кінематичний аналіз плоских систем
івизначення реакцій з’єднань
2.1.Короткі відомості про кінематичний аналіз
Класифікація плоских розрахункових моделей
Дослідження напружено-деформованого стану (НДС) споруд та їх елементів виконується по розрахункових моделях, які є оптимально ідеалізованими зображеннями елементів споруди, поєднаних певним чином в систему тіл з конкретними геометричними і фізичними характеристиками, та навантажень. Розрахункова модель, як фізична модель споруди, мусить максимально точно відображати властивості реального об’єкта і водночас бути доступною для розв’язування існуючим розрахунковим апаратом конструктора.
Розрахункові моделі бувають просторовими і плоскими. Не зважаючи на те, що плоскі схеми, здебільшого, значно простіші, вони дозволяють у багатьох випадках отримувати результати з потрібною точністю. Існують різні типи плоских багатоелементних і простих розрахункових моделей:
прості балки та балкові системи;
прості рами та рамні системи;
криволінійно-стержневі та аркові системи;
прості ферми та фермові системи;
гнучкі нитки;
пластинчасті системи;
комбіновані системи.
Тип будь-якої розрахункової моделі визначається геометрією її складових, характером їх взаємного розташування і поєднання між собою та видом зовнішнього навантаження.
Складові розрахункових схем та їх характеристика
Перший етап досліджень напружено-деформованого стану (НДС) споруди чи конструкції полягає в кінематичному аналізі розрахункової схеми, який крім оцінки можливості зміни геометрії споруди (зміни взаєморозміщення її складових частин) дозволить вдало вибрати метод та раціональну послідовність подальшого розрахунку. На цьому етапі всі елементи розрахункової схеми вважаються абсолютно жорсткими, тобто тілами, які не деформуються, а навантаження, як складову розрахункової схеми, взагалі не використовують. Обмежимось розглядом плоских розрахункових схем, всі складові яких (елементи конструкцій та навантаження) належать одній площині.

18
Розрахункові схеми утворюються із сукупності жорстких елементів – простих дисків, поєднаних у замкнену систему за допомогою ідеалізованих з’єднувальних пристроїв – в’язей.
Простий диск – будь-якої конфігурації суцільні стержні або пластини, які не утворюють жодного внутрішнього ізольованого контуру. Навколо простого диска, не перетинаючи його,
завжди можна здійснити безперервний замкнений “обхід”. На схемах далі прості диски позначатимуться літерою Д з нижніми числовими індексами знизу.
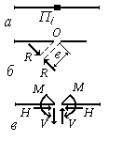
На рис.2.1 наведені приклади простих дисків, на яких пунктирними лініями показано замкнуті лінії “обходу” їхніх границь. Зокрема, простими дисками є довільної форми пластини (рис.2.1,а,б) прямолінійний (рис.2.1,в), криволінійний (рис.2.1,г) або складної конфігурації стержні (рис.2.1,
д,е).
Диск нескінченно малих розмірів перетворюється на матеріальну точку (рис.2.1,ж), яку далі називатимемо вузлом (на схемах позначається В). На рис.2.2 зображено пластину, яку не можна вважати простим диском, оскільки вона утворює ізольований контур, і, як зазначено раніше, при “обході” її контурів виникає потреба перетнути фігуру не менше одного разу.
Ступінь вільності тіла та ступінь змінюваності системи
Кількість незалежних геометричних параметрів, які визначають положення диска або системи дисків в довільній системі координат, називається ступенем вільності. На площині положення диска зі скінченними розмірами однозначно можна зафіксувати трьома незалежними узагальненими координатами (лінійними або кутовими). Для диска Д на рис.2.3,а такими координатами це xA , yA
та АВ. Для матеріальної точки В не існує кутової координати , тому ступінь вільності вузла дорівнює двом (рис.2.3,б).
а |
б |
Рис. 2.2 |
Рис. 2.3 |
Для системи дисків важливішою кінематичною характеристикою є ступінь змінюваності, яка чисельно дорівнює мінімальній кількості геометричних параметрів для визначення зміни взаємно-
19
го розміщення дисків, тобто положення всіх дисків в системі координат, пов’язаній з одним із дисків, який умовно вважатиметься нерухомим і називається «землею». Варіант вибору «землі» з усього загалу дисків замкненої системи не впливає на величину ступеня змінюваності системи, але інколи спрощуватиме хід кінематичного аналізу. Чисельно ступінь змінюваності замкненої плоскої системи завжди на три одиниці менший від її ступеня вільності.
Прості з’єднання
Ідеалізовані моделі пристроїв (без тертя та податливості) для поєднання окремих дисків та вузлів у систему (складений диск) з обмеженим взаємопереміщенням об’єктів, зменшуючи ступінь вільності складових та ступінь змінюваності системи називаються з’єднаннями. Кожне з’єднання характеризується кінематичними та статичними властивостями. Їх кінематичні властивості проявляються в незаперечності деяких узагальнених взаємопереміщень поєднаних ними дисків. Кількість таких переміщень дорівнює ступеню змінюваності системи. У подальшому на рисунках мо-
жливі переміщення будуть зображені контурними стрілками і позначені літерою . Статичні властивості з’єднань визначаються узагальненими реакціями (силами та моментами), які виникають у з’єднаннях між дисками по напрямках взаємних переміщень, що усуваються зазначеними з’єднаннями. В ідеальних з’єднаннях по будь-якому напрямку реакція та можливе переміщення несумісні.
Обмежимось розглядом лише деяких ідеальних з’єднань: припайка, муфта, циліндричний шарнір і кінематична в’язь.
Слід мати на увазі, що з’єднання можуть поєднувати лише диски (вузли), але не самі поєднуючі пристрої.
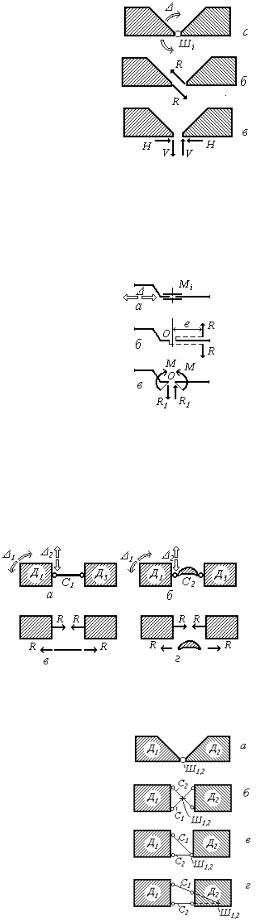
Проста припайка (Пi на рис.2.4,а) повністю виключає взаємні лінійні та кутові переміщення двох дисків, які з’єднуються нею. Це з’єднання зменшує кількість незалежних параметрів руху дисків на три, тобто усуває три ступеня вільності.
Реакція припайки це сила R, лінія дії та ексцентриситет e якої щодо центра припайки O заздалегідь невідомі (рис.2.4,б). Цю реакцію зручно представити як три складові, віднесені до центра припайки O: двох сил V і H із зручними для дослідження заданими напрямками, але невідомими модулями, та моменту M (рис.2.4,в).
20
Простий циліндричний шарнір (Ші на рис.2.5,а) з’єднує два диски, ви-
ключаючи можливість їхніх взаємних поступальних переміщень. Але він до-
пускає їх взаємний поворот відносно осі, яка проходить через центр шарніра. Отже, це з’єднання зменшує кількість незалежних параметрів руху дисків на два, тобто усуває два ступеня вільності.
Реакція R (рис.2.5,б), яка виникає у циліндричному шарнірі, являє собою силу, що проходить через його геометричний центр, але крім своєї величини
(модуля) має заздалегідь невідомий напрямок, які повинні бути визначені в подальшому розрахунку конструкції. При аналітичному розрахунку реактивну силу R звичайно замінюють на дві непаралельні складові V і H, які зручно обрати взаємно ортогональними
(рис.2.5,в).
Муфта (Mi на рис.2.6,а) допускає одне взаємне переміщення поступа-
льне переміщення двох дисків, які з’єднуються, уздовж фіксованої прямої – осі муфти. Це з’єднання зменшує кількість незалежних параметрів руху дисків на два, тобто усуває два ступеня вільності.
Реакція муфти представляє силу R, нормальну до напрямку можливого
Рис. 2.6
взаємного поступального переміщення дисків і розміщену з ексцентриситетом e відносно центра муфти O (рис.2.6,б). Звичайно цю реакцію замінюють на дві
складові силу R1 |
і момент M, відносячи їх до центра муфти O (рис.2.6,в). |
|
Кінематична |
в’язь ( в’язі С1 і С2, зображені на |
|
рис.2.7,а,б), що з’єднує два диски, перешкоджає поступаль- |
|
|
ному переміщенню одного диска відносно другого у напря- |
|
|
мку осі, яка проходить через точки шарнірного приєднання |
|
|
в’язей до дисків. Така в’язь усуває один ступінь вільності та |
|
|
допускає взаємний поворот 1 дисків і їх взаємне поступаль- |
Рис. 2.7 |
|
|
||
не переміщення 2 |
по нормалі до осі цієї в’язі. У кінематичній в’язі виникає реактивна сила R, лі- |
|
нія дії якої проходять вздовж осі в’язі (рис.2.7, в, г). |
|
|
Між різними простими з’єднаннями існує взаємний зв’язок, який надає змогу, якщо це необхідно або зручно, замінювати одні з’єднання іншими, не змінюючи при цьому їх кінематичні та статичні властивості.
Так, простий циліндричний шарнір Ш1,2 (рис.2.8,а), що усуває два взаємних поступальних переміщення дисків Д1 і Д2, можна замінити двома кінематичними в’язями С1 і С2 (рис.2.8,б), які перетинаються у центрі шарніра, котрий во-
ни замінюють.
Рис. 2.8
