Учебник системный анализ - Антонов

столько производных, сколько может потребоваться.

Аналогично разложим данную функцию в ряд в окрестности точкиХ

Это выражение представляет собой оценку значения интеграла.

Оценка может быть сделана как угодно точной, потому что можно взять

сколько угодно большое число членов в разложении функции в ряд Тей­

лора. Правило трапеций получается, если в формуле (12.9) отбросить

все члены, содержащие h в степенях выше первой. Таким образом,

ошибкапри использовании методатрапецийравна

Для малых h первый член гораздо больше всех остальных, поэтому ошибка именно им и определяется. Более того, в [8] показано, что за

счет наличия в выражении слагаемых с производными более высокого

порядка ошибка определяется следующим образом

Е == f'(x j+1)- f'(x j) h 2.

12

Полную ошибку интегрирования методом трапеций можно оценить сле­

дующим соотношением

Усовершенствованный метод трапеций. Попытаемся найти

более точное значение интеграла. для этого произведем сравнительно

простое усовершенствование метода трапеций. Рассмотрим ошибку

(12.11) и преобразуем данную формулу. На основании теоремы о сред-

нем значении можно написать

где а:5 ~ :5 Ь , так что

2

е = --h(b-a)f'(~).

12

Вданном выражении обозначим

С= -~(b-a)f'(~)

12 ~,

тогда ошибку можно записать

e=Ch 2 •

Предположим теперь, что вторая производная от интегрируемой функции является константой, тогда и С будет константой.

Выберем другую величину шагаразбиения отрезка интегрирования k = (Ь -а)/т, причем т *" n. Тогда получим выражение для ошибки ин­

тегрирования в виде

е=се.

Запишем далее значение интеграла, вычисленное по правилу тра­

пеций с шагом h - Ih И С шагом k - Ik • Тогда будут справедливы следу­

ющие выражения

I=I h +Ch 2 ,

(12.12)

1 =Ik +се.

Приравняем эти двауравнения друг другу и решим их относительно С,

получим

1

.11

l'

I i

Вычисленное таким образом значение интеграла является лучшим приближением, чем любое представление, полученное в (12.12). Если же вторая производная интегрируемой функции действительно посто­ янна на интервале интегрирования [а, Ь], то ошибка в формуле (12.13)

равна нулю.

Правило Симпсона. Способ интегрирования по правилу Симпсо­ на наиболее широко известный и применяемый метод численного ин­

тегрирования. В данном методе, так же как и в рассмотренных ранее,

интегрирование производится путем разбиения общего интервала ин­ тегрирования на множество более мелких отрезков. Однако в этом

методе для вычисления площади над каждым из отрезков через три

последовательных ординаты разбиения проводится квадратичная па­

рабола. Рассмотрим процедуру получения формулы Симпсона. Пусть,

как н ранее, n - количество отрезков разбиения интервала интегриро­

вания; h - ширина интервала разбиения. Предположим, что число n

является четным. Пусть k - ширина интервала при другом разбиении,

такая, что k = 2h. Тоща можно записать

I h =hl2(f(xo)+2f(x\)+2f(x2 )+···+2!(xn_\)+ !(хn»; (12.14)

(12.15)

Преобразуем выражение (12.13) учитывя,' что k = 2h, получим

Приведем подобные члены

I=4I k -Ih

3

Подставим данное выражение формулы (12.14) и (12.15), окончательно

получим

1h = и(хо)+4Лх\)+ 2!(х2)+4!(хз)+ 2!(х4) +... + +4Лхn_2) + 2Лхn_\) + !(х.»/З.

Данная формула называется формулой Симпсона. Ошибка при интег­

рировании с помощью формулы Симпсона равна

180

Как видно из данного выражения ошибка пропорциональна значе­

нию h4 в то время как для методатрапеций она была пропорциональна

h2• эТС:означает, что формулаСимпсона соответствуетряду Тейлора с

точностью до членов третьего порядка, а метод трапеций соответствует

этому ряду только с точностью до членов первого порядка. Поэтому

при интегрировании многочленов степени не выше третьего порядка

метод Симпсона дает точные значения интеграла.

Вычисление интегралов с бесконечными пределами. Рас­

смотрим еще одну важную задачу численного интегрирования - вычис­

ление определенного интеграладля случая, кощаодин или обапредела

интегрирования равны бесконечности. Таким образом, предм~м рас­

смотрения будет вычисление одного из следующих выражении

Поскольку вычислительная техника не работает с такими понятия­

ми как бесконечность, то задача аналитика состоит в том, чтобы за­

менить бесконечность реальным числом, обеспечив при этом прием­

лемую точность вычисления. Иными словами, необходимо найти такие

числа А и В, для которых были бы справедливы выражения

-А

ДЛЯ того чтобы процедура вычисления была реализуема, необхо­

димо, чтобы интегрируемая функция бьmа ограниченаиубываланагра­

ницах интегрирования. Изложение способа замены бесконечного пре­

дела конечным числом покажем на примере одного из пределов. для

других случаев процедуравычисления будет аналогичной. Нарис. 12.2.

видно, что функция стремится к нулю при стремлении аргумента к бес-

,,:

, '

1"

I

ЛХ)

fmax '6 L--_~~___""'::::~~___

::::G~.f;)~определитьчислоВ, котороебудетудовлетворятьypaB~

для определения числаВ на первом этапе необходимо ПОпытаться

~ценить максимальное значение интегрируемой функции которое она гfинимаетнаинтервале интегрирования. Пусть этозначе~иеравноi

Дредположим, что данное значение функция приобретает в точке~x'

пренебрежем. Наследующемэтапенеобходимонайтитакоеминималь'

ное значение аргумента х", для которого будет выполняться условие -

:~~о~~;~:~;~ше~ияинтегрируемойфункции(вслучае,~едставлен-

нице~, что Движение осуществляется влево отточки ~аксимума функ-

ции. сли интегрируемая функция отрицательна, определяют ее мини-

мум И ОСуществляют движениевсторонуееувеличения, соответственно-

вправо или влево, в зависимости от того, какой предел подлежит опре

12.4. Методы поиска оптимальноrо значения функции

с задачами оптимизации функции одной переменной впервые стал­

киваются при изучении математического анализа. Решают такие задачи

методами дифференциального исчисления. На первый взгляд может

показаться, что эти задачи относятся к достаточно простым и методы

их решения достаточно хорошо разработаны и изучены. Однако это не совсем так. Методы дифференциального исчисления находят ограни­ ченное применение. Особенно актуальной проблема становится при организации вычислительного процесса на ЭВМ. В данном случае тре­ буется разработка вычислительных процедур, реализующих численные методы поиска экстремального значения функции.

Рассмотрим постановку задачи. Пусть на числовой оси задано не­

которое множество Х, F(x) - функция, определенная на множестве Хи

принимающая во всех точкахх Е Хконечные значения. Для определен­

ности будем рассматривать задачу минимизации функции F(x) на мно­ жестве Х. Перейдем к рассмотрению численных методов решения за­

дачи поиска оптимального значения.

Метод деления отрезка пополам. Простейшим методом мини­ мизации функции одной переменной, не требующим вычисления произ­ водной, является метод деления отрезка пополам. Рассмотрим данный метод. Будем предполaгarь, что минимизируемая функцияF(x) унимодаль­ на на рассмагриваемом отрезке [а, Ь]. Поиск минимума на [а, Ь] начи­

нается с выбора двух точек х. = (а + Ь - Ь)/2 и Х2 = (а + Ь + Ь)/2, где

ь - постоянная, являющаяся параметром метода, О < 0< Ь - а. Вели­ чина Ь является параметром, определяющим точность решения. Точ­ ки Х1 И Х2 располагаются симметрично на отрезке [а, Ь] относительно

его середины и при малых 8 делят его почти пополам. После выбора точек Х1 и Х2 вычисляют значения F(x1) и F(x2) И сравнивают их между

собой. Если F(x1) ~ F(x2), то полагают а. = а, Ь. = х2; если F(x1) > F(x), то а.= х.' Ь.= Ь. Поскольку F(x) унимодальна на [а, Ь], ясно, что точка

минимума попадет на отрезок [ар Ь.]. Длина этого отрезка будет равна

Ь. -а. = (Ь-а -8)/2+8.

Данная процедура повторяется до тех пор, пока не будет достигну­ та заданная точность решения. При этом на k-M шаге точки для нового

F(X2k_l ) > F(X2k), то полагаем ak = x2k_l ' bk = bk_l • Полученный отрезок срав­ нивается с параметром, задающим точность вычисления bk - ak < Е. Если данное неравенство удовлетворяется, процесс вычисления оста­

навливают. Следует отметить, что Е > Ь; можно привести также сле­

дующие соотношения: количество разбиений определяется числом k> logzC(b - а - Ь)/(Е - Ь». Поскольку каждое деление пополам требу­

етдвух вычислений значений ФУНКЦИИ, то для достижения заданной точ­

ности требуется n = 2k > 21ogzC(b - а - Ь)/(Е - Ь» таких вычислений.

После определения отрезка [a k, bk] в качестве приближения к зна­ чению аргумента, в котором функция принимает минимальное значе­

ние, можно взять точку х. = X2k_1 при F(x2k_l ) ~ F(X 2k ) и х. = X2k при

F(X2k_l ) > F(x2k ), а значение F(x.) может служить приближением для ис­ комого минимального значения. Точность приближения в данном слу­

чае может быть оценена выражением (Ь - a)2-·12- I • Однако существу­

ют методы, которые за такое же количество итераций позволяют полу­

чить решение с большей точностью. Одним из таких методов являет­

ся метод золотого сечения.

Метод золотого сечения. Данный метод столь же прост как и

метод деления отрезка пополам, но он позволяет решить задачу с тре­

буемой точностью при меньшем количестве вычислений значений Фун­ кции. Золотым сечением отрезка является деление на две неравные части так, чтобы отношение длины всего отрезка к длине большей части равнялось отношению длины большей части к длине меньшей части

отрезка.

Золотое сечение отрезка [а, Ь] производится двумя точками

Х1 =а+(з-J5)(Ь-а)/2

и

Х2 =a+(J5-1)(Ь-а)/2,

расположенными симметрично относительно середины отрезка, причем

а< X 1< х2<Ь.

Следует обратить внимание на одно обстоятельство, а именно то,

что точка X 1' в свою очередь производит золотое сечение отрезка

[а, х2], аналогично точка Х2 производит золотое сечение отрезка [X 1, Ь]. Используя данное свойство золотого сечения, разработан следующий метод минимизации унимодальной функции на отрезке [а, Ь]. на пер­

вом этапе производят золотое сечение указанного отрезка и вычисля­

ют значения минимизируемой функции в точках X1' Х2: F(x ,) и F(x 2). Далее, если F(x ,) ~ F(x2), то за новый отрезок принимается [а, х2], т.е.

аl = а, ы = х2' если F(x ,) > F(x2), то аl = x l ' ы = Ь. Затем процесс деле-

ния отрезка методОМ золотого сечения про~олжаеvтся и вычисляются

значения минимизируемойфункциив каждоиновОиточке. Даннаяпро­

цедура выполняетсядотехпор, покане получим на некотором n-м шаге

отрезок Ь - а < Е, где Е - заданная точнОСТЬ. В качестве решения

выбирают'знач"ение функции, удовлетворяющее условию

Р(х') = rпiп(Р(а.),Р(Ьn»·

На этом процесс минимизации унимодальной функции заканчивается.

Метод прямого поиска. Рассмотрим еще один метод определе­

ния оптимальнОГО значения унимодальной функции на отрезке [а, Ь] и

нахождения значения аргумента, соответствующего оптимальному зна­

чению. В отличие от предыдущих случаев рассмотрим поиск макси­

мального значения. Суть метода заключается в следующем. На пер­

вом шаге необходимо определить направление поиска оптимального

значения функции. Для этого произвольнымобразомвыбираемдветоч­

ки х и х (рис. 12.3), в этих точках вычиСЛИМ значения оптимизируе­

же направлении. Пусть путем описанных вычислении достигнута точ-

Р(х)

ь х

а

Рис. 12.3. Метод прямого поискаоптимального значения функции

389

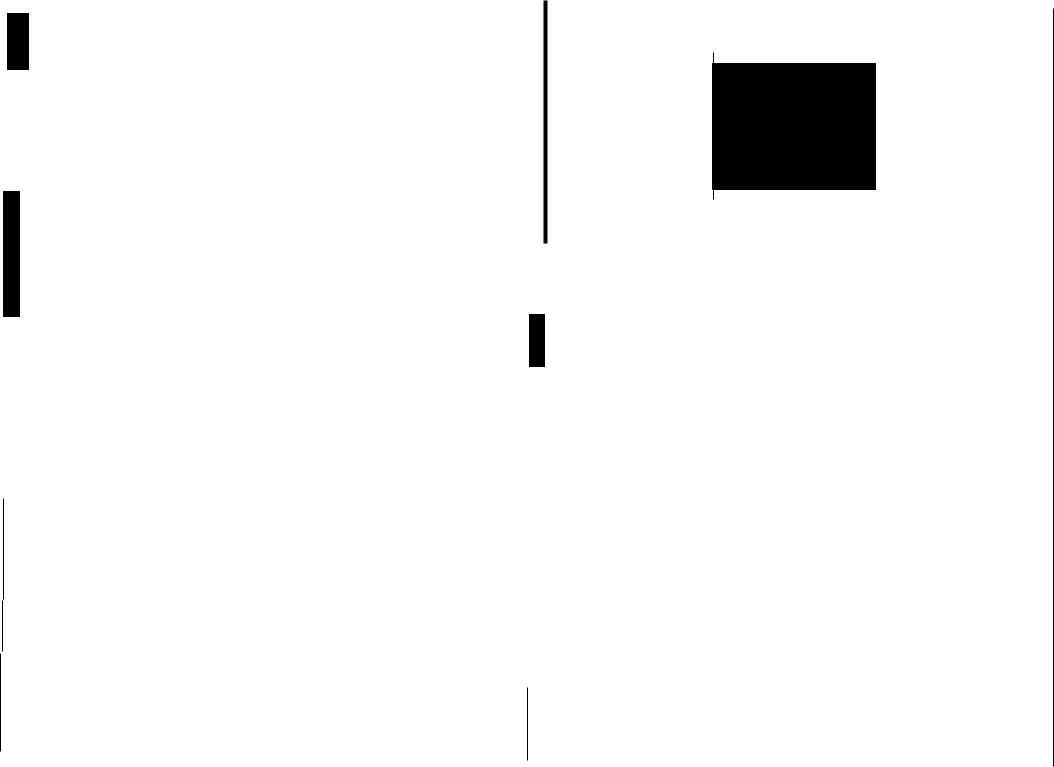
Kaxi +l · Вычисляем значение функции в данной точке и прОводим срав­

нение со значением в предыдущей точке, получаем F(x) > F(x + ). Ре­ зультат сравнения показывает, что в неравенстве знак поменялсяi I на

обратный. ЭТО говорит о ТОМ, что в процессе ВЫчислений значение

максимума функции осталось справа, Т.е. его проскочили. В ЭТОМ слу­

чае необходимоизменить величинушагаи поменятьнаправление дви­

жения. Положим дх = -дх/2 и определим новую точку х = х + дх

Поскольку новое значение шага беретсяс обратнымзнаком1+2,дВижение1+1 •

теперь ОСущеСТВляется в другую сторону, в данном Случае вправо.

Теперьдвижениевэтом направлениипродолжаемдотехпор,покавы­

полняется СООтношение F(x) < F(x + , ). Как только в данном неравен­ стве знак меняется на обратный, необходимоJ опять уменьшить шаг и

Изменить егознакдх = -дх/2. Путем таких итерацийпроцесс будет все

ближеи БЛижесходитьсякточке, в которойФУнкцияимеетмаксималь­

ное значение. Условием остановки процесса Вычислений будет дости­

жение заданной точности, которое можно СФормулироватьпутем зада­

ния соотНошения Ixk+1 - xk /:::::; Е. Полученное значение X + принимается за аРгумент, в котором функция Достигает маКсимума,kа1значение фун­

Кции в данной точке за оценку максимального значения.

12.5. Методы ПрЯМого поискарешений уравнений

Рассмотрим задачу ВЫчисления корней уравнения в случае, Korдa

Исследуемая функция в общем случае имеет трансцендентный вид.

ОтНосительновидафУНкциисделаем однопреДПоложение: будем счи­

тать, что фУНкция Монотонна на рассматриваемом участке. Пусть

имеем уравнение

F(x) = О.

(12.20)

Такая запись имеетдостаточно общий вид, например, если имеет­

ся уравнение в видеj(х) = g(x), то перенося правую часть влево, при­

ходим к выражению(12.20). Один из методов решения уравнений вида

(12.20) - метод последовательных приближений - был рассмотрен в

п. 12.2. В методепоследовательныхприближенийделалось предполо­

жение ОТносительнодифференцируемостифункции. В излагаемом ме­

тоде такого преДПОложения делать не будем.

Итак, ИЗложим метод поиска решения уравнения, аналогичного

методу ПОискаОптимальногозначения функции, раСсмотренногов пре­ дыдущем параграфе. Пояснение метода Поиска решения показано на

рис. 12.4.

390

F(x)

х

Рис. 12.4. Метод прямого поиска решений уравнений

На первом шаге произвольно выбираем точку Х1 и вычис~ем зна­

чение функции F(x ). Вначале определяем квадрант, в которыи попало

вычисленное значение1 Функции. Пусть ПОпучили, какизображенонарис.

124х > О значение функции также больше нуля. Далее выбираем шаг,

с~o~pым'будем осуществлять поиск решения, и вычисляем точкух2:

х = х - дх. В этой точке также вычисляем значение функции F(x ).

далееl определяем направление поиска решения. Если значение функ2 ­

ции в точке х больше чем в точке хl' то пересечение функци~ с осью

О динаг буде~ находиться справа от первоначально выбраннои точки.

!оответственнодвигатьсявпоискерешениянеобходимовправо.Если

же значение функции в точке Х2 меньше чем в точке х" то пересечение

функции с осью ординат будет находиться слева от первоначально В;Iб-

анной точки. И, следовательно, двигаться в поиске решения нео хо­

~имовлево так какэтоизображенонарис. 12.4. Определивнаправле

ние поиска' ос;ществляем движение с шагом дх до тех пор, показна~

чение функции, не станет меньше нуля, т.е. покафункциянеизменитсвои

знак Как только произошло изменение знака функции напротивополож-

'(точках ) необходимоизменитьнаправлениедвижения,приэтом

НЫИv осуществляетсяпоискре-

необходимо 1+1также изменить шаг, с которым

шения' дх = -дх/2. Теперь начинаем двигаться в противоположную

сторону с меньшим шагом. Движение в эту сторону также идетдотех

по показначение функциинеобходимоизменило свой знак. Кактолько произошло

из~~нениезнакафункции, сноваизменитьнаправлениепо­

иска ешенияближеуменьшить шаг. Ясно, что в процессе такого поиска

еше~иевсе иближесходитсякнулю.Условиемостановкипро­ Рцессавычисленийбудетдостижениезаданнойточности,которооемож­

но сформулировать путем задания соотношения /хk+1 - хk/ <- Е.) суще-

ствляя данную процедуру, находим решение уравнения (12.20 .

391

Подведем итоги. В данном разделе представлены некоторые типы

задач и изложены основные подходы к их решению. Рассмотренные

методы не претендуют на полноту охвата всей теории численныx ме­

тодов. Реально теория численных методов является самостоятельной

развивающейсяДИСциплиной, сширокимспектромразделов. Например, имеются хорошо разработанные и представленные в литературе мето­

ды решения дифференциальных уравнений, интегральных уравнений

Вольтерра и ФреДГОльма, всевозможныx Систем уравнений и Т.П. раз­

делы. Данные процедуры представлены в специальной литературе.

ЗдесьставиласьцельИЗЛОжитьподходы крешениюЗадач иотдельных

Процедур, широко встречающихся в Системных исследованиях.

В заключениеостановимсянанекоторыхрекомендацияхпоприме­

нению численныx методов. Приступая к решению Задачи Системных

исслед~ванийцелесообразнее начинатьрешение срасчетаПростейших

моделеи, изучать модели с ИСПОльзованием ПРОстейших проверенных

методов. Лишь после всестороннего анализа и уяснения всех аспектов

задачи имеет смысл заниматься расчетом Сложной модели с примене­

нием грОмоздких по своей Структуре процедур.

Обратим Внимание на некоторые опасности, с которыми может

столкнутьсяСистемный аналитикприприменениичисленныхметодов

для решения задач. При алГОРИтмизации математической задачи с це­ лью ее решения численными методами могут возникнуть ситуации,

преПЯТСТВующие успешному получениюрезультата, аименно:

v а) имеется Qпасность замены Исходной задачи задачей, не имею­

щеи отношения к исходной постановке.

б) алгор~тм, применяемыйдляреш'ениязадачи, приВОЗМОжностях

современнои ВЫЧИслительной техники не поддается расчету.

Такимобразом,необходимотщательноивсестороннеанализировать

постановкузадачи. Исследование постановкизадачидаетВОЗМОЖность

начать изучение ее с простейшей модели с последующим УСложнени­

ем метода и программы решения задачи. Важно отметить, что при решении задач численными методами большое Внимание следует уде­

лятьразработке и применению специальныхтестов и Отладочных про­

грамм. Применение процедур контроля и тестовых проверок дает ис­

слеДователю уверенность в успешном решении задачи.

Глава 13

ВЫБОР ИЛИ ПРИНЯТИЕ РЕШЕНИЙ

13.1. Характеристика задач принятия решений

Теория принятия решений представляет собой набор понятнй и сис­

тематических методов, позволяющих всесторонне анализировать про­

блемы выбора и принятия решений, в том числе в условиях неопреде­ ленности. Цель теории - совершенствование процесса принятия реше-

Реализация выбора и принятия решений явля:тся ОДНОИ И; завер­

шающих процедур системного анализа. За дaнHO~ процедурои следу­

ет внедрение результатов системных исследовании. В процессе приня­

тия решения реализуется цель системного анализа, которая был~.сфор-

мулирована на соответствующих этапах пр~ведения исследовании. «Вы­

бор является действием, придающим всеи деятельнос:и целенаправ­ ленность. Именно выбор реализует подчиненность всеи деятельности определенной цели или совокупности целей» [1]. Таким образом, при­ нятие решений является обязательным, центральным этапом систем­ ных исследований. Перед реализацией процесса выбора считаются выполненными два крайне важных этапа или процедуры системных исследований - определение целей системного анализа, для достиже­ ния которых собственно и осуществляется выбор, и генерирование аль­

терюrrив, т.е. порождение множества альтернатив, на K~POM предстоит

осушествить выбор. В этом случае принятие решении можно рассмат­

ривать как операцию над множеством альтернатив, в результате выол-­

нения которой множество сужается до подмножества выранныыx аль­ тернатив. В идеальной ситуации подмножество должно состоять ИЗ

одной альтерюrrивы. Эта ситуация желательна, но не всегда реализуе­ ма. Итак, при выполнении процесса принятия решений осуществляется

анализ альтернативных способов действия, приводящих к достижению заданных целей. Важным обстоятельством является также наличие

критериев, с помощью которых осуществляется сравнение вариантов

достижения целей. Задание критериев или мер эффективности позво­ ляет определить степень, с которой заданные цели могут быть достиг-

393

11

1

нуты С помощью различных способов действия. для каждого способа

действия возможные исходы описываются в единицах принятых мер

эффективности.

Таким образом, для того чтобы приступить к решению задач вы­ бора, необходимо сформировать и детально проанализировать пресле­

дуемые системными аналитиками цели, задать исходное множество

альтернатив, из которых требуется выбрать наиболее предпочтитель­

ные, а также определить критерии оценки и сравнения любых альтер­

натив. Но даже при выполнении всех перечисленных условий проблема

выбора не тривиальна и допускает существенно различающиеся под­

ходы к своему решению. Сложность решения задач выбора обусловле­

на их особенностями. Рассмотрим их.

1. Многоцелевой характер задач системного анализа. При проведе­

нии системных исследований приходится стремиться к достижению различных частных целей. В общем случае цели могут быть противо­

речивы. Продвижение по пути достижения одной цели может приводить

к ухудшению результатов по другим. В такой ситуации лицо, принима­

ющее решение, неизбежно оказывается перед необходимостью выбо­

ра между противоречивыми целями.

2. Воздействие фактора времени. Все важные последствия приня­

того решения сразу не проявляются и нельзя указать конкретный мо­

мент времени, когда можно наблюдать то или иное последствие.

3. Наличие неформализуемых понятиЙ. Такие понятия как добрая

воля, престиж, политические действия и тому подобные часто имеют место при проведении системных исследований, в особенности при ана­

лизе социотехнических систем. Эти понятия являются неформализуе­

мыми понятиями, которые существенно усложняют задачу принятия

решений.

4. Неопределенность. Маловероятно, что в момент принятия реше­ ния, т.е. выбора альтернативного действия, будут досконально извест­

ны последствия каждой из альтернатив.

5. Возможность получения информации. Часто можно организовать работу по сбору информации об объекте исследования, которая может

помочь в решении задачи выбора альтернативного способа действия.

Однако следует учитывать, что собираемая информация всегда требу­

ет затрат средств и времени и к тому же она практически всегда обла­ дает ограниченной достоверностью.

6. Динамические аспектыI процесса принятия решений. После того,

как некоторое решение выработано и выбрана альтернатива, может

оказаться, что задача не исчерпана до конца, и потребуется принять

очередное решение через определенное время. Принятое решение мо-

жет способствовать одним и препятствовать другим решениям, кото­ рые будут приниматься в будущем. Важно распознать заранее такие динамические проблемы и увидеть, какие возможности могут открыть­

СЯ в будущем благодаря тому или иному решению.

7. Влияние решений на структурные звенья объекта системных ис­

следований. Некоторая выбранная альтернатива может повлиять на

работу различных структурных элементов объекта системных иссле­

дований, например коллектива исполнителей того или иного подразде­

ления. Принятое решение может затруднятьработуодних и способство­

вать работе других коллективов исполнителей.

8. Коллективное принятие решений. Часто ответственность за вы­

бор альтернативы несет не отдельное лицо, а группа исполнителей.

Фактически для определенного круга задач нельзя четко разграничить функции и ответственность лиц, принимающих решение по некоторому

Сформулированные особенности задач принятия решении позволя-

ют подойти к их классификации. В основу классификации задач приня­

тия решений положены следующие принципы: число лиц, принимающих решение; вид показателя эффективности; уровень определенности ин­ формации, на основании которой принимается решение; зависимоСть элементов модели проблемной ситуации от времени.

По признаку числа лиц, принимающих решение, различают задачи

индивидуального, принимаемого одним лицом, и группового принятия

решений, когдарешенияпринимаются коллективныморганом. Пригруп­

повом выборе решений определяющую роль играет проблемаvсогласо:

вания индивидуальных предпочтений членов группы. Главнои задачеи

на этом этапе является объединение предпочтений отдельных лиц в единое мнение. Степень согласованности целей при многостороннем

выборе может варьироваться от полного совпадения интересов сторон

(кооперативный выбор) до их противоположности (выбор в конфлик­

тной ситуации). Возможны также промежуточные случаи, например

компромиссный выбор, коалиционный выбор, выбор в условиях на­

растающего конфликта и Т.д. Решение задачи объединения предпоч­

тений отдельных лиц в единое мнение можно достичь в рамках теории

экспертного оценивания.

В зависимОСТИ от вида используемого показателя эффективности

задачи принятия решений подразделяются на однокритериальные и мно­

гокритериальные. Задачи с одним критерием называются скалярными,

многокритериальные задачи - задачами с векторным критерием эф­

фективности. Следует иметь в виду, что в задачах с несколькимИ кри­ териями эффективности различные цели могут противоречить друг

l'

1,

I

11

:1

другу. Также необходимо учитывать, что критерии могут иметь как

По признаку степени определенности информации о проблемной

ситуации различают задачи ПРинятия решений с ПОЛНостью заданной

ИСходной информацией, требуемой для решения проблемы, и задачи в

условиях наличия неопределенности. Задачи Принятиярешений в усло­ виях определенности называютсядетерминированными задачами. Они

характеризуются наличием полной и достоверной информации о про­

блемнойситуации, критерияхэффективности,ограниченияхипослед­

ствиях, реализующихся в Процессе Принятия того или иного решения.

ЗадачиПРИнятиярешенийвУСЛОвияхнеопределенностихарактери­

зуются наличием стохастической инестохастическойнеопределеннос­

ти.

Характернаяособенностьзадач ПРИнятиярешений в условияхнео­

пределенности заключается в том, что исход операции зависит как от

стратегии, выбираемойлицом, принимающимрешения, такиотнеопре­

деленных факторов, не известныхлицу, ПРинимающемурешенияв мо­

мент его выработки.

По признакузависимости элементов моделипроблемнойситуации

от времени различают статические и динамические задачи. Элементы

модели в динамических задачах зависят от функций времени, описы­

вающих поведение динамических объектов, и тем самым значительно

УСЛОжняют процедуры выработки решений.

Режим выбора может быть однократным (разовым) или Повторя­

ющимся, допускающим обучение на опыте.

Различные сочетания перечисленных вариантов и приводят к мно­ гообразным задачам выбора, которые изучены не в одинаковой степе­

ни. В зависимостиоттипазадач принятиярешенийиспользуютразлич­

ные методы выработки решения. Рассмотрим некоторые методы и

подходы к решению задач выбора и принятия решений.

13.2. Критериальный способ Описания выбора

Наиболее развитым и чаще всего применимым при решении задач выбораЯВляетсякритериальныйподход. Припримененииданногопод­

хода предполагается, что каждую отдельно взятую альтернативу мож­

но оценить численно, значением критерия. Тогда сравнение альтерна­

тив сводится к СОпоставлению соответствующих им чисел.

В зависимости отобъектаицели исследования критерии или пара­

метры оптимизации ~OГYT быть весьма разнообразны. Чтобы ориен-

396

тироваться в этом многообразии, введем некоторую классификацию. Итак, среди множества параметров оптимизации выделяют: экономи­

ческие,технико-экономические,технологические,статистические,ПСИ­

хологические, эстетические и т.п. Примерами экономических парамет­ ров могут служить прибыль, рентабельность, себестоимость; технико­

экономических - производительность, надежность, долговечность;

технологических - выход продукта, характеристики качества и пр.

Критерий или параметр оптимизации - эт~ признак, ~o кото­

рому оптимизируют процесс nринятия решении. Критерии должен

быть количественным, задаваться числом. Необходимо уметь измерять

его при любой возможной комбинации воздействующих на исследуемую

систему факторов. Множество значений, которые может принимать критерий (параметр оптимизации), называют областью его определе­ ния. Области определения могут быть непрерывными и дискретными, ограниченными и неограниченными~ Например, BЬ~XOД реакции - это параметр оптимизации с непрерывнои, ограниченнои областью опреде­ ления. Он может изменяться от О до 100%. Число бракованных изде­

лий число кровяных телец в пробе крови - примеры параметров с дис­

кре;нойобластьюопределения, ограниченнойснизу.Еслинетспособа

количественного измерения результата, то приходится пользоваться

подходом, называемым ранжированием (ранговым подходом). В этом

случае параметрам оптимизации присваивается оценка - ранг по зара­

нее выбранной шкале. Ранг - этоvколичественн~я оценка параметра оптимизации. Она носит условныи субъективныи характер. Чаще все­ го ранжирование используется в тех случаях, когда требуется оценить качественный признак. Ранговый параметр имеет дискретную область определения. В простейшем случае область содержит два значения (да - нет, хорошо - плохо). Это может соответствовать спvособу оценки качества продукции, является она годной или бракованнои. J3Pугим при­ мером субъективной оценки может служить оценка знании на экзаме­ не. Знание - абстрактный параметр. В этом случае оценка знания осу­

ществляется путем проставления ранга, определенного, скажем, по пя­

тибалльной шкале.

Для каждого физически измеряемого параметра оптимизации можно построить ранговый аналог. Потребность в построении такого аналога

возникает, если имеющиеся в распоряжении исследователя численные

характеристики неточны или неизвестен способ построения удовлетво­ рительных численныхоценок. При прочихравных условиях всегда ~o отдавать предпочтение физическому измерению, так как ранговыи под­ ход менее чувствителен и с его помощью трудно изучать тонкие эф­ фекты.

Е:ли теперь сделать еще одно важное предположение, что выбор

любои альтернативы приводит к однозначно известным последствиям

(т.е. счита::ь, что ВЬ~бор Осуществляется в условиях определенности)

и заданныи критерии q(x) Численно выражает Оценку этих последствий

то наилучшей альтернативой х· является, естественно, та, которая об~

ладает наибольшим значением критерия:

398

Сведение многокритериальной задачи к однокритериальной

Рассмотрим наиболее употребительные способы решения много­ критериальных задач. Первый способ состоит в том, чтобы многокри­ териальную задачу свести к однокритериальноЙ. Это означает введе­ ние суперкритерия, т.е. скалярной функции векторного аргумента:

qoCx ) = qo (q,(x), qix), ... , q/x)).

399

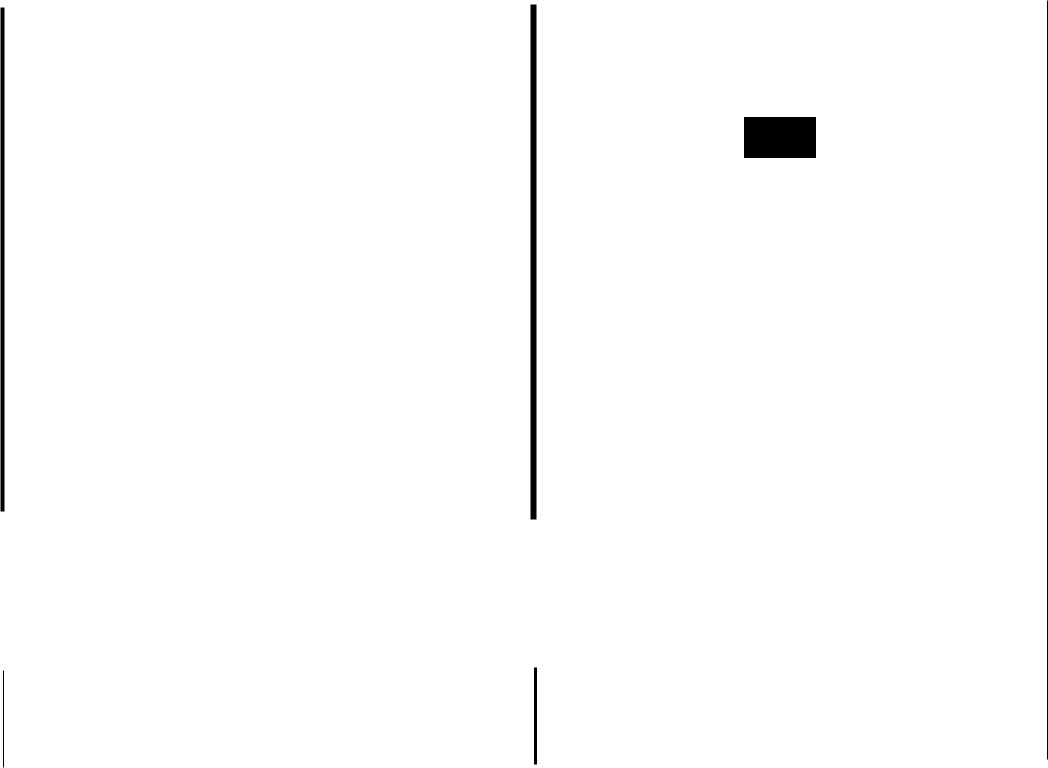
Суперкритерий позволяет упорядочить альтернативы по величине qo' выделив тем самым наилучшую (в смысле этого критерия). Вид

функции qo определяется тем, как мы представляем себе вклад каж­ дого критерия в суперкритериЙ. Обычно для реализации данной проце­

дуры используют аддитивные

..f. a,q. qo = L-'-' .

1=1 Sj

или мультипликативные функции

l-qo = U(I-P~~jJ.

Коэффициенты S/ обеспечивают безразмерность критериального значения (частные критерии могут иметь разную размерность, и тогда некоторые арифметические операции над ними, например сложение, не

имеют смысла). Коэффициенты а./, ~/ отражают относительный вклад

частных критериев в суперкритериЙ.

Итак, при данном способе задача сводится к максимизации супер­

критерия:

х· = arg тах qo (qj (х),..., qp (х», при х Е Х.

Очевидны: достоинства объединения нескольких критериев в один

суперкритерии сопровождаются рядом трудностей и недостатков, ко­

тopыe необходимо учитывать при использовании этого метода. Расс~отрим примеры построения обобщенных критериальных по­

казателеи. Пусть рассматриваемая альтернатива характеризуется n

час}ными крите~иальными функциями q j(i= 1, 2,.. ,р). Каждая из функ­

ции qj имеет свои физический смысл и, чаще всего, свою размерность.

Введем простейшее преобразование: набор данных для каждого q. по­

ставим в соответствие с caMыM простым стандартным аналог~м -

шкалой, на которой имеется только два значения: О - брак, неудовлет­

ворительное качество, 1 - годный продукт, удовлетворительное качест­

во. В ситуации, когда каждый преобразованный критерий принимает только д~a значения О и 1, естественно желать, чтобы и обобщенный критерии принимал одно из двух возможных значений, причем так, что­ бы значение 1 имело место тогда и только тогда, когда все частные критериальные показатели приняли бы значение равное 1. Если же, хотя бы одинuиз показателей принял значение, равное О, то и обобщенный критерии будет paBHыM нулю. В этом случае для построения обобщен­ но:о критериального показателя естественно воспользоваться форму­

лои

400

Иногда применяют запись

i.'

r

где qo - обобщенный критериальный показатель; q/- частные крите­

риальные функции.

Если для каждого из частных критериев известен «идеал», к кото-

рому нужно стремиться, то можно предложить следующий метод по­

строения обобщенного параметра оптимизации (критериального пока­

зателя). Пустьq/О-наилучшее(идеальное)значениеi-гoкритерия. Тогда (qj _ q/O )- мера близости к идеалу. Поскольку при построении обоб­

щенного критериальногопоказателя необходимо, чтобыразличные по­

казатели были сопоставимы, надо привести их к безразмерному значе­ нию. Это можно осуществить, отнормировав полученное отклонение

следующим образом

(qj - qjQ)/ q/о.

Чтобы исключить влияние знаков, возведем последнее выражение в

квадрат

((qj - qjQ)/ qjQ )2.

Тогда обобщенный критериальный показатель можно записать

qo = f«q;o -q)1 q;o)2.

;=1

Если все частные критерии совпадают с идеалом, то qо станет рав­ ным нулю. В таком правиле определения обобщенного критериального

показателя каждый частный критерий входит в формулу наравных пра­

вах. На практике показатели бывают далеко не равноправны. Введем

некоторыевесовыекоэффициентыa.j , тогдаправило определенияобоб­

щенного параметра можно записать в виде:

qo = fa,;«q;o _q)lq;O)2, причем fa,; =1, a,j >0.

i=l i=l

Задача определения значений весовых коэффициентов- это отдель­

", .. ;

ная задача; она не входит в рамки обсуждения.

401

26-4355