Учебник системный анализ - Антонов

Глава 9

НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ

АНАЛИЗА СТАТИСТИЧЕСКОЙ

ИНФОРМАЦИИ

9.1. Общие замечания

Pa~CMoтpeHHыe ранее параметрические методы анализа статисти-

::~~~~~~Ф~~~~~~~:е~~~~е~~:;:Iт:~~пд~~е::а:тсякритикеспециа-

параметрических методовтребует пре~положений~ ::еп;:к~::ение

пределениянаблюдаемыхслучайныхвеличин.Какправило нельзяРy~:~

зать какие-либо веские пр ,

ниерезульта;овнаблюден=;~~~~:~:~~~~~~~~oH=~:T:~:eP:~;~~~;;:~na

::~=~:::I~~~~Т:~йн~:::~::Jне~::ь:ь~:~~т~~:~~:~z:~:~:к~~:аp:~~

пределения, произведениетаких величин приближается лога иф

ноgмальнымраспределением.ВтеориинадежностиДоказ~ном:;;~~

~~моткидоотказаоднотипныхэлементовподчиняютсяэкспон~нциаль-

ся в~:з~~::Jа~:~~е:зев::~~Р::оТ~Му:~Раасктлучер. ~тказов предполагает-

подавляю :ддер;ку того или иного семейства законов распределения. В

для испол~~:а~:шинствереальныхситуацийподобных обоснований

жены и изучены статистические критерии, основанные на использова­

нии эмпирического процесса. Но непараметрические методЫ, в кото­

рых не делается никаких нереалистических предположений о том, что

функцияраспределениярезультатов наблюденийпринадлежиттемили

иным параметрическим семействам распределений, стали заметнОЙ

частью статистического анализа только во второй трети ХХ в.

После Второй мировой войнЫ развитие непараметрических стати­

стических моделей пошло быстрыми темпами. Большую роль в разви­

тии этих методов сыграли работы Вилкоксона и его школы. К настоя­

щему времени с помощью непараметрических методОв можно решать

тот же круг задач, что и с помощью параметрических. Все большую

роль играютнепараметрические методы оценкИ плотности, непарамет­

рические подходы в решении задач регрессионного анализа и теории распознавания образов. В настоящем разделе рассмотрим непарамет­ рическиеметодыоценкиплотностираспределения.Построивплотность распределения, можнодалеепереходить копределениюширокогокру­

гастатистическиХпоказателеЙ. Поэтомузадача оценки плотностирас­

пределениянаблюдаемойслучайнойвеличиныявляется одной изклю-

чевых задач статистическогО анализа.

9.2. ГистограммныЙ метод восстановления

плотности распределения

для приданиянаглядностистатистическомуматериалуего необхо­

димО подвергнуть дополнительной обработке. С этой целью строится

статистическиЙ ряд. Покажем, как осуществляется его построение.

Пусть имеются результаты наблюдения над непрерывной случай­

нойвеличинОЙХ,оформленныеввидепростойстатистическойсовокуп­

ности. Рассмотрим весь диапазон зафиксированных значений велиЧИ­

ныХи разделим его на интервалы. Диапазон зафиксированных значе­

нийслучайнойвелИЧИНЫ представляетсобойобласть определения дан­

нойвеличинЫ.Далееподсчитаемколичествозначенийреализовавшейся

случайнойвеличины,попавшихвкаждыйинтервал, обозначим этизна­

чения через т;" Каждое из полученных значений разделим на общее

число наблюдений n и определим частоту попадания случайной вели-

чины в i-й интервал наблюдения:

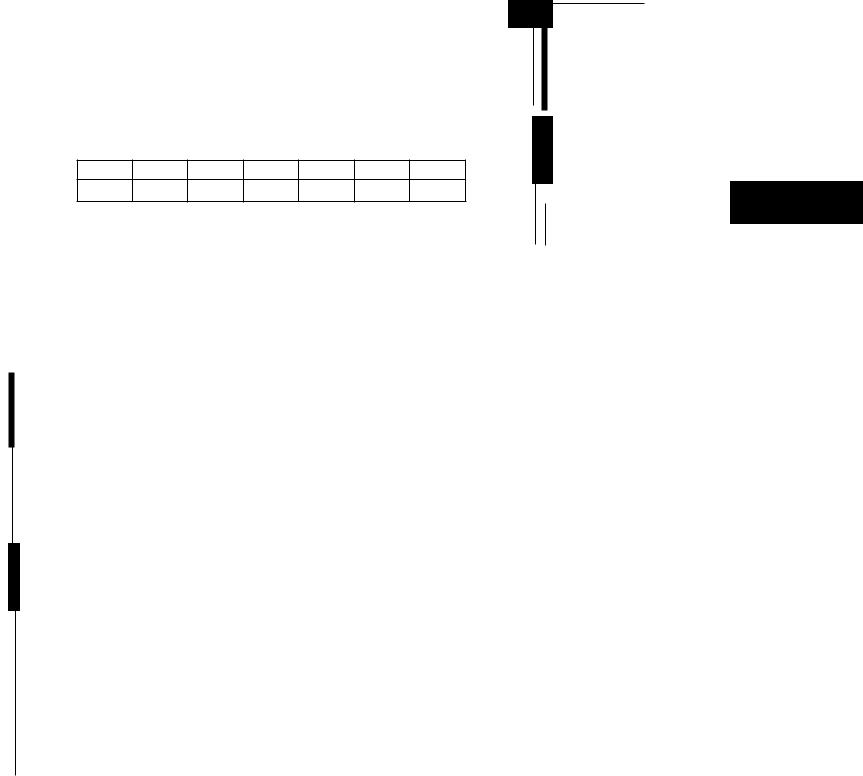
Сумма частот всех интервалов должна быть равна единице. Пред­ ставив полученные результагы расчетов в виде таблицы, получим ста­ тистический ряд (см. табл. 9.1).

Таблица 9.1

Здесь 1/ - обозначение ,"-го интервала; Х/; X i+1 - границы данного интервала; Р; - соответствующая частота; k - количество интервалов.

При построении статистического ряда возникает вопрос о рекомен­

дуемом количестве интервалов разбиения области определения наблю­ даемой случайной величины. С одной стороны, количество интервалов не должно быть слишком большим, в этом случае ряд распределения становится невыразительным и частоты в нем обнаруживают незако­ номерные колебания; с другой стороны, оно не должно быть слишком малым, при малом числе интервалов свойства распределения описы­ ваются статистически слишком грубо. Чем богаче и однороднее ста­ тистический материал, тем большее число интервалов можно выбирать при составлении статистического ряда. В математической статистике

известна формула Стаджесса, с помощью которой вычисляется коли­

чество интервалов разбиения области определения случайной величи­ ны. Согласно этой формуле количество интервалов определяется сле­ дующим образом:

k = 1+ З,Зlgn.

При построении стагистического ряда возможны различные способы выбора длины интервалов; они могут бьnъ как равными, так и различны­ ми. Однако следует отметить, что в практике построения стагистическо­ го ряда наибольшее применение нашли два: метод равных интервалов и

равночастотный метод. В первом методе, естественно, длины интервалов

выбираются одинаковыми. Во втором методе длины интервалов различ­ ные. Они выбираюгся таким образом, чтобы количество попаданий слу­

чайIjОЙ величины в каждый из интервалов бьmо одним и тем же.

Графическое представление статистического ряда называется ги­

стограммой. Гистограмма строится следующим образом. По оси абс­

цисс откладываются интервалы и на каждом из них строится прямоу­

гольник, площадь которого равна частоте данного интервала. для по-

строения гистограммы необходимо частоту каждого интервала разде­ лить на его длину и полученное значение взять в качестве высоты пря­

моугольника. В случае равных интервалов высоты прямоугольников

пропорциональны соответствующим частотам. Из правила пос:,Роения гистограммы следует, что полная площадь под гистограммои равна

единице. Формулу построения гистограммы можно представить в сле-

дующем виде:

гдеI[Х;Е A.uJ - индикатор, равный единице, если условие в скобкахвы­

тить значительную потерю информации, связанную с тем, что иссле­ дователю для построения гистограммы необходимо знать, сколько на­

блюдений попало в выбранный интервал разбиения и абсолютно не важ­

ныприэтомзначениянаблюдений. Во-вторых,принципразби:ния (рав­

ных интервалов или Paв.\lыxчастот), а также число разбиении, являют­

ся некоторыми «степенями свободы». Как исследователь выполнитраз­

биение воспользовавшись такой свободой, зависит только от него.

в-трет~их, скорость сходимости гистограммной оценки к плотности

крайне низкая.

Рассмотрим пример построения гистограммы п~ результатам на-

блюдения заслучайной величиНОЙ, характеризующеи наработкидо от­

каза группы однотипных объектов. Пусть результаты функционирова­

ния группы однотипных объектов представлены в виде статистическо-

го ряда, приведенного в табл.9.2.

Таблица 9.2

285

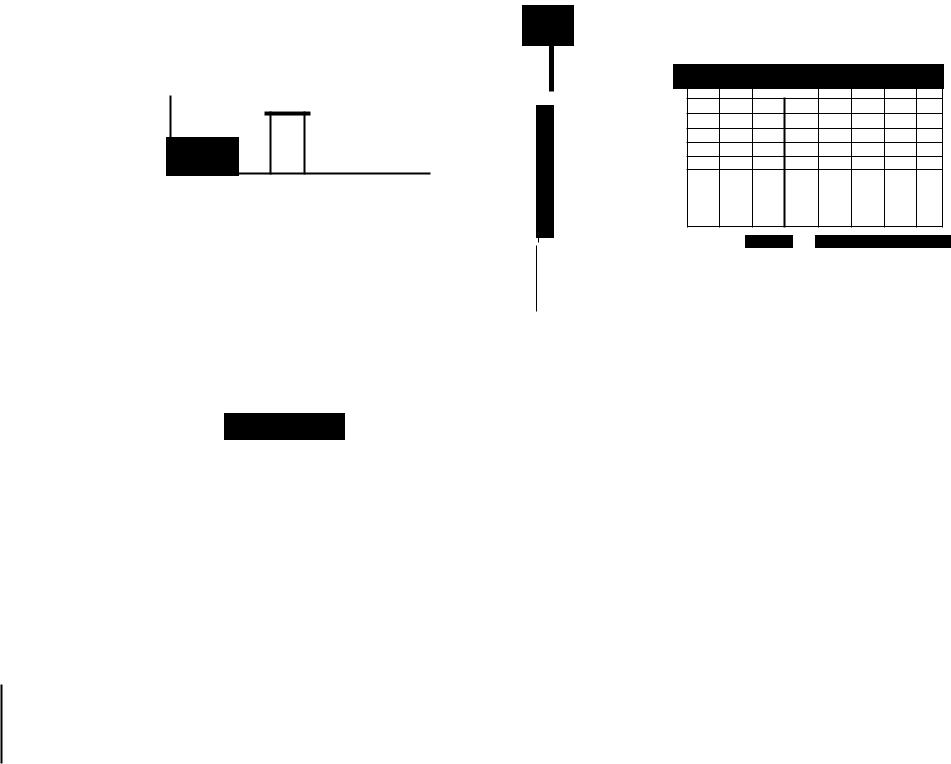
На основанииданнойтаблицы построим гистограмму (рис.9.1).

~/n

2/n

1/n

Рис. 9.1. Пример построения гистограммы

Пользуясь результатами построения стаТистического ряда можно

постр~ит~такжеэмпирическую функциюраспределения наблю'даемой

случаинои величины. для этого необходимо определить значения Ф н­

кциираспределениянаграницахинтервалов,по которымпОстроена~и­

стограмма, тогда получим

F(O,~)=O;

~ F(~,X2)=PI; F(~,Хз) = Р1 + Р2;

F(xk,oo) = L Р; =1.

;=1

Эмпирическая функция распределения будет представлять собой

ступе~чатуюфункцию, изображеннуюнарис. 9.2. Построениеэмпири

ческои функции распределения решает задачу описания статистичес~

286

m/n

Рис. 9.2. Эмпирическая функция распределения

9.3. Построение эмпирической функции распределения по цензурированной выборке

Анализ работ по непараметрическим методам оценивания харак­

теристик сложных систем на основании цензурированных данных по­

казывает, что достаточно полно разработаны и исследованы методы

получения точечных и интервальных оценок для случаев, когда у ис­

следователя имеются большие объемы статистических данных.

В [38] изложены методы построения оценки функции F(t), исследо­ ваны свойства этой оценки, рассмотрены методы оценивания некото­

рых показателей надежности на основании цензурированных данных

незначительного объема. При оценивании характеристик объектов на

основании информации, полученной на этапе их эксплуатации в составе

штатного оборудования сложных систем, возникают ситуации, анало­

гичные рассмотренным в [38], а именно, распространенной является ситуация, когда информация представлена в виде цензурированныхдан­ ных весьма ограниченного объема. Поэтому методы, изложенные в [38],

можно эффективно применять при проведении экспресс-анализа харак­

теристик объектов сложных систем на этапе проведения системных ис­ следований. Рассмотрим метод построения эмпирической функциираспре­ деления, изложенный в [38].

Пусть имеется функция распределения F(t), тогда вероятность по­ падания наблюдаемой случайной величины в интервал (О, 1) будет рав­ на F(1). Разобьем интервал наблюдения на k равных частей. Опреде­ лим вероятность попадания наблюдаемой случайной величины в интер-

вал (О, ~.] для любого j = п.

1

" 11

I

Попадание случайной величины на некоторый интервал (О, ~.] есть

событие, которое можно представить как сумму событий, состоя'щих в

том, что случайная величина попадет либо в интервал (О, ~. 1]' либо в

~ервал (~j_1' ~). Следовательно, для вероятности попаданiiя случай­

нои величины в интервал (О, ~) можно записать выражение

- условная вероятность попадания случайной величины в интервал

(~j-l'~) приусловии, что на интервале (О, ~.-t] случайная веЛичина Тне

реализовалась. 1

Подставляя выражение (9.2) в (9.1), получаем формулу для опре­

деления вероятности попадания случайной величины Т в интервал

(O,~) ,

(9.3)

где Q(~J.:.I) - вероятность попадания случайной величины в интервал

(О, ~j_t]·l'асписывая аналогичным образомвероятность попадания слу­

чайной величиныв интервал(О, ~j-l] через вероятностипопаданияв ин­ тервалы (О, ~j-2] И (~j-2' ~j-t]' получаем

Q(;j-l) =Q(;j-2) +(I-Q(;j-2»Q(;j_2';j_l 1;j-2)'

Повroряяданнуюпроцедурудляинтервалов(О,~i]'где 1< i <j, можно

В конечном счете получить выражение для вероятности попадания на­

блюдаемой случайной величины в интервал (О, 1) в виде

k

Оценимфункциюраспределениядлямногократноцензурированной

- значения наблюдаемой случайной величины среализовавшимся при-

знаком; Т;, j = 11 +1,11 +V - значения наблюдаемой случайной величины

с нереализовавшимся признаком, Т.е. цензурированные данные.

288

Разобьем результаты наблюдения на k интервалов:

чайной величины с нереализовавшимся признаком, попавших вj-й ин­

тервал,

Для определения оценки функции распределения в точке t необхо­

димо вместо значений величин Q(~j-t)' Q(~j-t' ~/~j-t) В (9.4) подставить

их оценки. В качестве условных вероятностей используют отношение

количества реализаций J.Lj , попавших на интервал (~j_1' ~), К общему

числу объектов, находящихся под наблюдением в начале этого интер­ вала при условии, что в начале интервала под наблюдением находится

хотя бы один объект. Если в начале интервала под наблюдением отсут­

ствует хотя бы один объект, то условная вероятность наблюдения слу­ чайной величины на этом интервале равна нулю. Поэтому оценку ус­ ловной вероятности на интервале полагают также равной нулю. С уче­

том этого выражение для оценки функции распределения в точке t бу­

дет иметь вид

;=1

Если в первом интервале одна или несколько случайных величин с

нереализовавшимся признаком меньше первой случайной величины с

реализовавшимся признаком, то V0"# О, в противном случае V0= О. Если

в последнем интервале значение последней случайной величины с реа­

лизовавшимся признаком больше всех значений случайных величин с

нереализовавшимся признаком, то Vk = О, В противном случае Vk"# О.

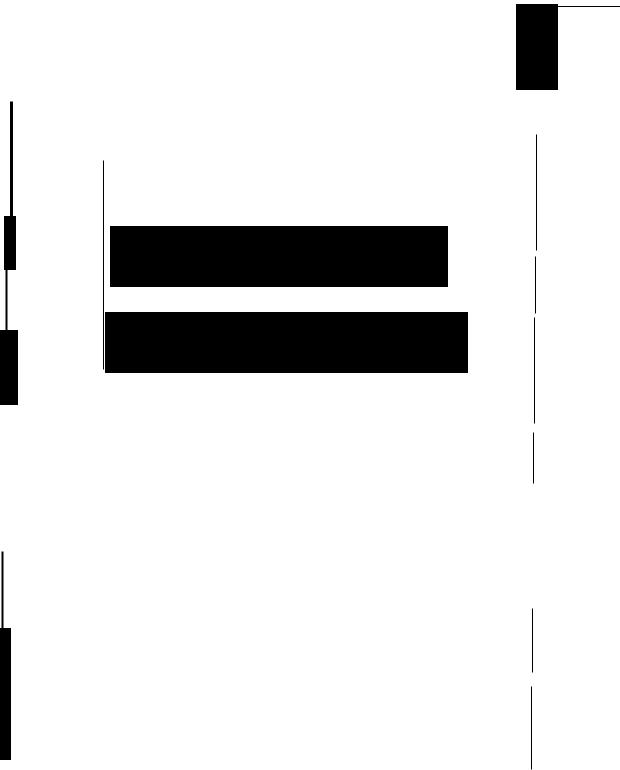
1

11'"

"

I{ I

I

I

"1':'1

111,

I

",1'1

,"

,,'

,1

Величина Nyi' ВХОдящая в выражение (9.5), называется УСЛОвным

объемом цеНЗурированной выборки на интервале (~J-t' ~). Она равна

числу объектов, за КОТорыми ведется наблюдение на указанном интер­

вале.

Выражение(9.5) можно переписать, несколькодетализировав пред­

ставление функциираспределения на каждом интервале:

Оприt::;;О;

Ni1 при О::;; t ::;;;р i1 = О, 1, ..., 111;

уl

j;(t) =

В [38] даютсярекомендациидляразбиения области, накоторойпро­

водится Оценивание ФУНКЦИИ распределения, на интервалы. В частно­ сти, указано, что для ПОвышенияТОЧНости оценкиF(t) необходимо весь

отрезок наблюдения [О, 1], где T=;k = тax[~,Т:], разбитьнаинтервалы,

границы которыхСОвпадают со значениями случайныхвеличин с нере­ ализовавшимс~признаком. Например, есливыборку наблюдений, состо­

ящую из случаиныхвеличин с нереализовавшимся признаком и случай­

ныхвеличин среализовавшимся признаком записать в порядкевозрас­

тания ее членов в виде

II

а J.Li' vроответственно будут равны

111 =2, У1 =1; 112 =1, У2 =1;...; I1k =2, vk =0.

Ес~и в выборке наблюдений окажется, что отдеЛьные значения

случаиныхвеличин среализовавшимся признаком будутравны некото-

290

рым значениям случайных величин с нереализовавшимся приз~аком, то в вариационном ряду (9.8) сначала указывают значения слу;аиных ве­

личин с реализовавшимся признаком, затем значения случаиных вели­

чин с нереализовавшимся признаком.

Таким образом, используя правило (9.7), можно строить эмпиричес­ кую функцию распределения случайной величины при многократно цен­

зурированных выборках.

9.4. Ядерная оценка плотности

Гистограммные оценки плотности распределения, рассмотренные в предыдущих параграфах, обладают существенным недостатком, а

именно, плотность или функция распределения, полученные данным методом, являются ступенчатыми функциями. Реальные функции рас­

пределения являются непрерывными функциями. Следовательно, гис­

тограммные оценки хорошо аппроксимируют 'рУнкции распределения только в случае больших объемов наблюдении, когда n ~ 00. В ситуа­

ции, когда наблюдения производят за функциональными характеристи­

ками сложных систем, хотелось бы иметь более гладкие оцен~и плот­

ности ИЛИ функции распределения. Шагом в получении такои оценки явилась модель построения так называемой ядерной оценки плотнос-

ти. ]

Ядерные оценки впервые бьmи введены в работах Парзена [44 и Розенблатта [45]. Рассмотрим методику построения ядерных оценок

для плотности распределения непрерывной случайной величины. Пусть

в результате наблюдения за объектом исследования получена выборка

Т1, Т2, Тn' На основании данных результатов построим гистограмм­

ную оценку ФУНКЦИИ распределения. Гистограммную оценку функции распределения будем строить несколько отличающимся способом по сравнению с тем, как это было сделано в п. 9.2. Буде~ полагать, что изменение функции распределения происходит в каждои точке наблю­

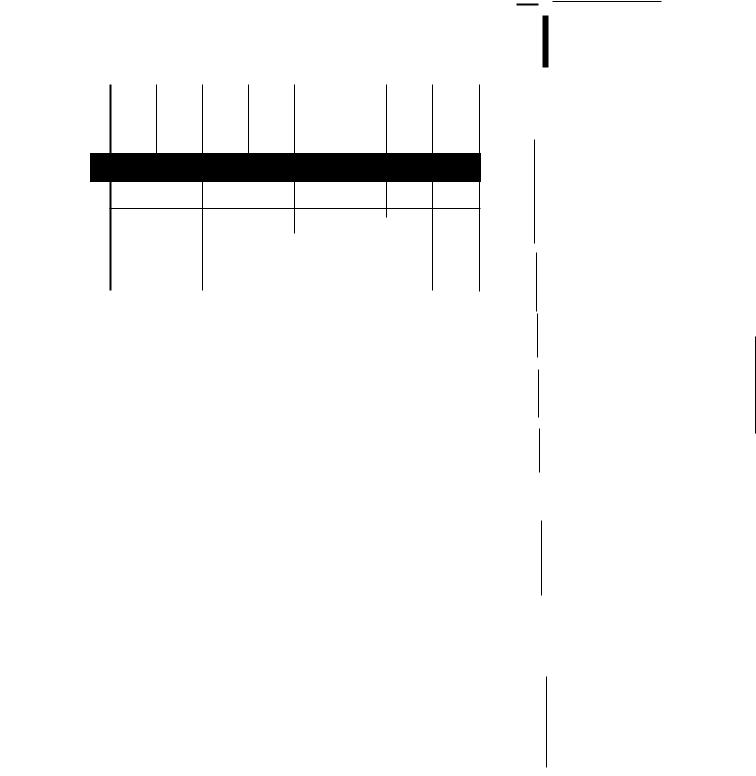
дения, причем величина такого изменения равна 1/n. Построенная та­ ким образом ФУНКЦИЯ распределения изображена на рис. 9.3. Ее можно

записать в виде

F(t)

ления пока не очень высока и не отличается в лучшую сторону по срав

нениюФ сгистограммным представлением. Заменим в выражении (9 1О)-

ункциюДираканекоторойконечнойфункцией,удовлетворяющейс~й­

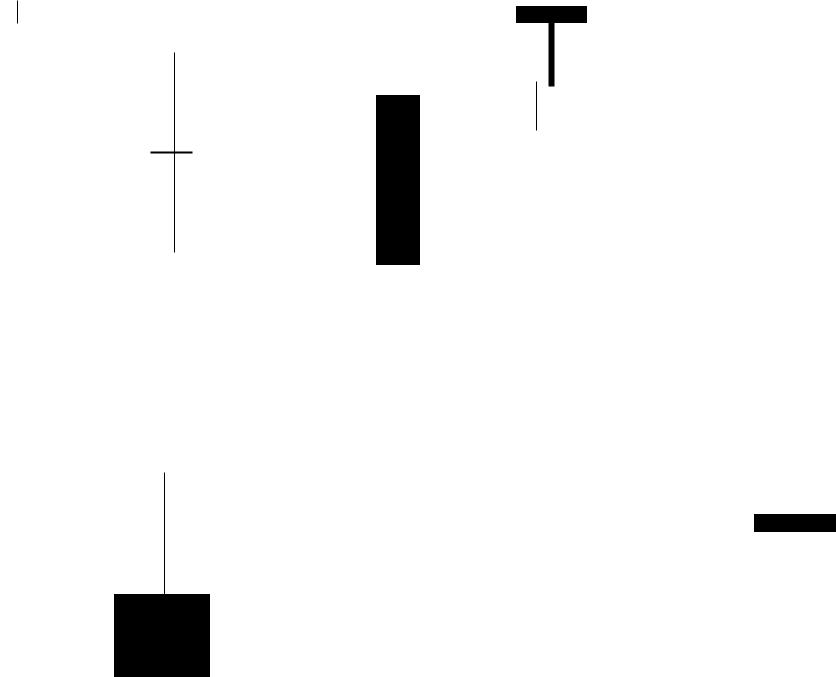
Вид функции представлен на рис. 9.4. Если в качестве ядра взять дан­ ную функцию и сузить интервал определения, Т.е. определить ее на ин­

тервале [-h, h], h < 1, то получим оценку плотности в виде

Плотностьраспределения,построеннаянаоснованииформулы(9.13),

будет представлять собой непрерывную функцию. В последующих за

исследованиями Парзена и Розенблатта работах бьmо предложено

множество других функций, используемых в качестве ядра. Отметим

некоторые из них. Так называемаятреугольная (рис. 9.5) функция име-

етвид

о при t<-I,

1+ t при -1::; t < О,

Тг = 1 при t == О,

1- t при О < t ::; 1,

О при t > 1.

Широкоеприменениеприпостроенииядерныхоценокплотностирас­

пределения находит функция Гаусса

1 (х2 )

G(t) = J21texPl2

Изображение функцииприведено нарис. 9.6.

Ядерная оценка плотности распределения будет получаться путем

подстановкиввыражение(9.13) соответствующегоядра,например,G(t)

вместо ядра K(t). Так, для гауссовского ядраполучим выражение плот-

Качество восстановленной с помощью ядерного оценивания плот­

ности зависит от выбора величИНЫ параметра h. Параметр локальнос-

293

тем определяем значение плотности в точке Tt • В результате получа­

ем Inl-I (h.,~). На следующем шаге исключаем значение Т2• На осно­

вании оставшихся значений Т.' ТЗ' ... , ТN строим плотность In2 (hl't).

_1

Далее вычисляем значение ядерной оценки плотности в точке Т2• По­

лучаем In2 (h Т2). Повторяем данную процедуру по всем T до Тn. По-

_1 l , j

лучаем массив {1:-.(I!.,7;)}, i=l,n. На основании вычисленных значе­

н»й оценок плотностей в точках строим функцию правдоподобия

L(h.,1';) = п 1:-. (hl'T).

i=1

На втором этапе устанавливаем значение константы h, равное h2, и повторяем описанную процедуру заново. Вычисляем функцию правдо­ подобия

L(h2 ,1';) = п1:-1 (h2 ,1';) И т.д.

;=1

Оптимальное значение h выбираем как результат решения выраже­

ния

h"m =argmaxL(h·,n.

h. J

J

Данная процедура сложна в реализации, но обеспечивает вычисле­

ние оптимального значения параметра h.

В работе [46] приводятся результаты исследования сходимости ядерных оценок. В частности отмечено, что оптимальная скорость схо­

димости ядерной оценки плотности обеспечивает выбор параметра h

на уровне

(9.14)

где а= fK2(t)dt, ~=(ft2K(t)dt)2 fl"(t)2dt. При этом также предполага­

ется, что hn~ О, nhn ~ 00, при n ~ 00 иf(t) - ограниченная плотность,

имеющаядвенепрерывныепроизводные, и f (f"(t»2 dt < 00 . Данныйре­

зультат также можно использовать для определения оптимального зна­

чения параметра h. В приведенной формуле (9.14) неизвестным пока­ зателем является плотностьf(t), используемая для определения коэф­ фициента ~. Заменим данную плотность ее ядерной оценкой. Посколь­ ку ядерная оценка зависит от параметра h, то для поиска оптимального

значения параметра необходимо организовать итеративную процедуру проведения расчетов. На первом этапе выбираем произвольное значе-

ниепараметраh l <1. дляданногозначениястроимядернуюоценку плот­

НОС~И!,.(h.. t) инаееоснованиираССчитываемзначенияКОЭффициентов

ициентов а, ~. Повторяем данную процедуру до тех пор, пока не бу­

дет ВЫПОЛняться УСЛОвие сходимости результата вЫчисления оптими­

9.5. Проекционное оценивание

плотности распределения

Следующимшагом вразвитиинепараметрическихметодовоцени­

ванияплотностираспределениянепрерывнойслучайной велИчиныяви­

лись проеКЦИОнныеметоды. Впервыеметод оценивания плотности ас

~peд~~~,получившийназваниепроекционный, бьшпредложенJpa~

OT~ . . енцова[47]. для построения оценки плотностираспределе­

:: ьшииспользованы~езультагытеорииОртогональныхфункций.для

илучения проекционнои оценкиЧенцов использовалразложение функ­

~eивP[ri'1Ф]~ьe. Итак, пустьf(t) - функция, имеющаяобластьопреде­

ния , . ледовательно, ее можно разложить в ряд Фурье:

f(t) = LCj<l'/t),

j=1

где {q>P)} - ортонормированнаятригонометрическая Системана [0,1].

<1'2/ (t) = J2 cos 27tlt;

<1'2/+1 (t) =J2sin 2тtlt;

<1'1 (t) =1, 1~ 1.

Оценка ФУНКцииf(t) тогда будет определяться по формуле

Т.е. в раз~ожении в ряд Фурье берется конечное число членов сумми­

рования. ценкикоэффициентоввразложенииопределяютсяпоформуле

296

Оценка (9.15) называется проекционной оценкой Ченцова. Условие t Е [О, 1] не ограничивает общности. Функцияf(t) может быть опреде­ лена на любой ограниченной области D ЕЮ. Отнормировав данную область, можно обеспечить условие t Е [О, 1]. После построения плот­ ности распределения на интервале [0,1] необходимо выполнить обрат­ ный переход в область определения функции D.

В выражении (9.15) неопределенной осталась величина N, которая представляет собой число слагаемых в разложении функции в ряд Фу­ рье. Данный параметр называется параметром сглаживания. В [46]

отмечается, что тригонометрическая система недостаточно богата для

оценивания любых плотностей. Однако этот недостаток уравновеши­

вается рядом преимуществ проекционных оценок, в частности их пре­

ВОСХОДНЫМ поведением в случае, когда разложение плотности распре­

деления в ряд содержит конечное число членов или является бесконеч­ ным с быстро убывающими коэффициентами. Известна оценка для оп­

ределения оптимального числа гармоник Nn состоящая в следующем:

(9.16)

j=N+1

В литерагуре (например [48]) приводится значительное количество

ортонормальных систем, которые можно использовать для построения

проекционных оценок плотности распределения. Помимо тригономет­ рической системы это полиномы Лежандра, которые образуют ортонор­ мальную систему на [-1, 1], оценки с рядом Эрмита. Функции с рядом Эрмита образуют ортонормальную систему, определенную на [-<х>, 00]. Оценка с рядом Лагерра образует также ортонормальную систему, определенную на [О, 00]. Ортонормальная система Хаара отличается от всех предыдущих тем, что она является базисом в области определе­ ния [О, 1]. Формулы разложения для данных систем, а также свойства

проекционных оценок с этими разложениями приведены, например, в

[48].

297

I

,1

I

,1,l'

сти::::~о~ф~;:::и~:сслпе::ь~хтрехглавахметодыобработкистати-

ментов,COCTaB~ЫXчастейипо;:~~~::~:~::~:~::~~:~~;~

роения моделеи Систем. Рассмотренные методы обработки ИнФорма­

ДЫ, включающие в себя гистогра

Оценки. ПредставленныйматериалПР~::~~е~~~::I~о~~~екционные

:атистических показателей Сложной системы с высокойН~~е~~::~

чности и соответСтвенно высокой дОСтоверностью. Высокая степень достоверности оценок достигается за счет ИСПОльзования цензуриро

ван~~и~ан~ых, атакжезасчетИСпользованияаприорнойинФормации~

ВОпросов,~а~=;~~сi~~~::в:::~о:с~~~~:нз:геоР:~:~;~енкомплекс

:итаци~~ныхмодел~~С~~ак:::Ч~::~~~~;:~~О:;~:~;к::~~~;:~~

МОделеи и оценки параметров систем.

Глава 10

МАТЕМАТИЧЕСКОЕ ПРОГРАМ~РОВАНИЕ

Методы математического программирования представляют собой

класс моделей, применяемых для формализации задач планирования целенanpавленнойдеятельности, предусматривающих распределение ограниченного количества ресурсов разных видов. Подобного рода

задачи решаются в различных отраслях деятельности: в экономике,

при разработке проектов, составлении расписаний, планировании во­

енных операций и т.п. Модели математического программирования

относятся к категории детерминированных моделей. Термин програм­

мирование в применении к рассматриваемому типу задач понимается

как поиск наилучших планов (от английского слова programming - со­ ставление плана, программы действий). Когда говорят о задачах ма­

тематического программирования, имеют в виду задачи, цель которых

состоит в повышении эффективности промышленных, транспортных

систем, систем управления деятельностью учебных, проектных, на­ учных организаций.

Математическое программирование подразделяется на линейное, целочисленное, нелинейное, динамическое программирование. Рас­

смотрим некоторые постановки задач, методы и алгоритмы их реше­

ния.

10.1. Математические постановки задач, приводящие

к моделям линейного программирования

Задачи линейного программирования относятся к категории опти­ мизационных. Они находят широкое применение в различных облас­ тях практической деятельности: при организации работы транспорт­

ных систем, в управлении промышленными предприятиями, при состав­

лении проектов сложных систем. MHome распространенные классы

задач системного анализа, в частности, задачи оптимального плани­

рования, распределения различных ресурсов, управления запасами, ка-

299

лендарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования. Несмотря на различные области приложения данные задачи имеют единую постановку: найти

значения переменных х!' х2,.", Хn ' доставляющие оптимум заданной линейной формыz= e1xl+ еТХ2+"'+ еnхn при выполнении системы огра­

ничений, представляющих собой также линейные формы. Рассмотрим примеры конкретных постановок задач, формализация

которых приводит к моделям линейного программирования. Вначале рассмотрим задачу определения оптимального ассортимента. Имеет­

сяр видов ресурсов в количествах ы' Ь2,... , Ь" ... , Ьр и q видов изделий.

Задана матрица А =lIajj 11, где a/j характеризует нормы расхода i-гo ре­

сурса на единицу j-ro изделия (;=1, 2, ... , q). Эффективность выпуска

единицыj-го изделия характеризуется показателем ер удовлетворяю­

щим условию линейности. Требуется определить план выпуска изделий (оптимальный ассортимент), при котором суммарный показагель эффек­ тивности принимает наибольшее значение. Обозначим количество еди­

ницj-го изделия, выпускаемых предприятием, через Х}' тогда матема­

тическая модель задачи будет иметь следующий вид:

определить максимум линейной формы тахZ = LCjX j

j

при ограничениях на ресурсы Laij ~ Ь;о i = 1, 2, ..., р.

Кроме указанных ограничений по ресурсам в модель могут быть

введены дополнительные ограничения на планируемый ~ьmyCK продук­

цИИ Х. ~ XjO' условия комплектности изделий и Т.п.

Прирассмотрениитиповыхзадачсистемного анализабылирассмот­

рены задачи распределения ресурса, в числе которых описаны задачи,

возникающие при проектировании систем, а именно, задача составле­

ния титульного списка и задача определения оптимальной очередности

разработки. Приведем их формулировки в развернутой постановке.

Задача составления титульного списка. Сформулирован пере­

чень задач, решаемых на первом этапе автоматизации. После состав­ ления перечня задач, включаемых в первый этап разработки, необхо­ димо оценить требуемый состав ресурсов на их разработку и требуе­ мое время для их внедрения. Пусть время, требуемое на разработку задач, превышает заданный срок ввода первой очереди в эксплуатацию, тогда возникает проблема составления титульного списка, Т.е. возни­

кает необходимость ограничения перечня задач, автоматизируемых на первом этапе. Проблема выбора комплекса задач из сформированного

перечня в условиях дефицита времени и ресурсов на разработку всего

300

перечня задач выполняемых на первом этапе автоматизации, называ­

ется задачей ~оставления титульного списка. Таким образом, форму­

лировказадачи будет выглядеть так: требуетсяvсформировать переч:~

задач подлежащих автоматизации (титульныи список), с учетом и

Формализуем данную задачу. Введем обозначения: пусть l - номе

задачи' 1 _ полное их число; т- заданное время разработки и BHeд~e~

;-

зачи' Х _ переменная, принимающая значение 1, ес.ли задача вклю­ожидаемыиv эффект от внедрения l-иния первой, очереди системы; е

ч:тся'в ~итульный список, и О- в противном случае;) ~ индексресур­

j-гo ресурса для i-й задачи будет определяться следующим о разом.

т

Wjj = JTjj(t)dt.

о

П сть В _ суммарная величина наличияj-го ресурса в систе~е.

даНН~IЙпоdазательможно определитьчерез величинуRP) п(~~к:{;)

есурса поступающего для разработки и внедрения системы - - .

~уммарная величинаj-гo ресурса определяется по формуле

т

B j =JR/t)dt.

о

8 _ максимально допусти-

Определим еще одну характеристику Tjj . ботки

мое значение потребляемого потока ресурса)-го вида д~ ~азР;хнюю

и внедрения i-й задачи. Данная величина представляет со ои ве

гра~~~::::~:~;i~ениятитульногоспискаможносформулировать

в следующем виде:

1

максимизироватьлинейную форму LCjXj

не превышал имеющегося количества данного ресурса, выделяе­

~~~ для решения i-й задачи. Второе ограничение говорит о том, ч~~

максимально допустимое значение потребляемого ресурса не ~:ж