
Учебник системный анализ - Антонов
.pdf
|
|
г |
D12 |
|
|
|
|
|
|
|
|
||
|
|
v=г1 = ~~l |
D |
22 |
D. ] |
|
|
|
|
2n |
, |
||
|
|
Dn1 |
Dn2 |
Dnn |
|
|
|
л |
при i = j; |
|
|
|
|
где D.. = |
D(e) |
|
|
|
|
|
л |
л |
|
|
|
|
|
и |
{ соу( ер e ) при i'# j. |
|
|
|
|
|
|
|
j |
|
|
|
|
Приведем формулы для определения дисперсии параметров зако
нов распределения для двухпараметрических плотностеЙ. Пусть а и
~ - оцениваемые параметры плотностиf(а, ~, (). Пусть определены
элементы информационной матрицы
ii
l'
:1'
1,./(,"
" |
|
:f~ |
Экспоненциальное распределение |
.i' |
|
|
Рассмотрим имеющее важное прикладное значение экспоненциаль |
ное распределение. Например, данное распределение широко исполь
зуется в теории надежностидля описания случайной величины наработки
до отказа. Плотность экспоненциального распределения имеет вид
I,(л, (); функция распределения Fэ(л, () = 1 - ехр(-Лt). Параметр л назы
вается интенсивностью отказов. Запишем функцию правдоподобия
~(л,t)=ЦлеХР(-Л1';)=лn ехр(-Л~1';}
Для определения оценки параметра л необходимо решить уравне-
ине
где |
|
|
|
|
|
a2Z(a,p,t) |
aZ(a,p,t) |
|
|
дадР ; а22 = |
др2 |
Дискриминант матрицы равен |
|
|
|
Dis = ~la22 -a~2. |
(7.3) |
||
Тогда дисперсию параметров а'и ~ определим по формулам |
|||
D |
а |
= _!!в... . |
(7.4) |
|
Dis' |
|
|
D |
~ |
=-!1L |
(7.5) |
|
Dis |
|
|
Ковариация будет вычисляться следующим образом: |
|
||
соу(а,р)= -~. |
(7.6) |
||
|
|
Dis |
|
Перейдем к рассмотрению примеров применения метода макси
мального правдоподобия для оценивания параметров некоторых зако
нов распределения, имеющих важное значение в задачах системного
анализа.
202
После дифференцирования получаем оценку максимального правдопо добия параметра экспоненциального закона распределения
i=_n_.
tr.
1=1
Дисперсия оценки параметра л характеризует точность этого парамет
ра и равняется
Для интенсивности отказов, зная оценку параметра и ее дисперсию,
можно определить доверительный интервал с заданной доверительной
вероятностью. Если обозначить верхнюю и нижнюю оценки интенсив
ности отказов через "-в и ЛИ' то можно определить
л i |
л i |
ЛВ = Л+ гп t~, ЛИ = Л - гп t~, |
|
где t - табулированная величина, которая зависит от уровня доверитель
ной JJвероятности ~ и определяется обратным интерполированием рас
пределения Стьюдента [37, табл. 6.2].
Определение среднего времени между реализациями событий про изводится по формуле
203

интервальные оценки равны
1 |
1 |
ТН =-л- |
, ТВ =-л- • |
Ав |
Ан |
Вероятность безотказной работы определяется следующим обра
зом:
Рэ(t,А) = exp(-At),
соответственно интервальные оценки вычисляются так:
~1(t,A) = ехр (-Анt);
РВ(t,A) = ехр (-Авt).
Рассмотрим далее пример оценивания параметров нормального
закона распределения.
Нормальное распределение
f(t,т,O') = ~1 ехр(т-t)2) v2nO' 20'2'
Функция правдоподобия имеет вид
n ( |
1 |
n |
lN(т,O',t) =-- |
ln2n+ln0'2 ) -- L(T - т)2 |
|
2 |
20'2 |
1=1' • |
для определения оценокмаксимального правдоподобия параметров
т и а2 необходимо решить систему уравнений
al(т,O',t) =_1 ~ |
_ |
_. |
|
||
дт |
л 2 |
"-(~ |
|
т)-О, |
|
О' |
1=1 |
|
|
|
|
al(т,O',t) _ |
n |
1 |
n |
л |
2 |
д0'2 --26'2+2(Л2)2L(~-т) |
=0, |
||||
|
|
О' |
1=1 |
|
|
откуда получаем
204
л 1 ~ |
л 2 |
_ 1 ~(T Л)2 |
|
т=-k~, |
О' |
-- ""' |
I- т . |
n 1=1 |
|
n 1=1 |
|
Определим точность в оценивании данных параметров. для этого вычислим вторые производные функции правдоподобия по параметрам:
a2 1(т,0'2,t)
дт д0'2
Дискриминант информационной матрицы будетравен
2 |
|
Dis=_n_ |
|
26'6 , |
|
откуда получаем |
|
6'2 |
26'4 |
D[т]=-; D[0'2]=-. |
|
n |
n |
Таким образом, рассмотрен метод оценки параметров законов рас
пределения и определения точности в их оценке. Рассмотренные при
меры определения параметров законов распределения имеют важное
прикладное значение. Как было указано, экспоненциальное распреде
ление применяется в теории надежности для описания наработок до
отказа объектов. Область применения нормального закона распреде
ления еще более широка. Он используется для описания погрешностей,
дрейфов параметров, наработок до отказа механических изделий, для
которых не удается выделить доминирующей причины, приводящей к
отказу, для описания времени обслуживания систем и т.Д.
7.3. Оценка вероятностных показателей систем путем
обработки цензурированных данных
Постановка задачи при обработке цензурированных выборок фор
мулируется следующим образом. Пусть имеется выборка объема r = k+v, котораясодержитряд наблюдений за функционированием объек тов среализовавшимся признаком Т)' Т2,.. • , Tk (полные наработки), и ряд
205

I i
I
11
'11'
!"I
наблюдений с нереализовавшимся признаком т..:т;,...,т:. Пусть извес
тен закон распределения времени до реализации наблюдаемого признака F(8, (). Оценим параметры закона распределения. Функция правдопо добия для выборки, содержащей цензурированные наработки при цен зурировании справа, запишется следующим образом:
v |
k |
|
Ln (G,t) = П(1- F(G,I;') )Пf(G,Тj). |
(7.7) |
|
1=1 |
j=1 |
|
для цензурированной выборки при цензурировании слева функция прав доподобия имеет вид:
v |
k |
|
Lл(G,t) = П(F(G,I;') )Пf(G,Тj). |
(7.8) |
|
1=1 |
j=1 |
|
Процедура получения оценок параметров аналогична изложенной в п. 7.2. А именно, необходимо прологарифмировать функцию правдопо добия, взять от нее производную по искомому параметру и приравнять ее нулю. Например, в случае цензурирования справа решение будет выглядеть следующ"м образом. Логарифм от функции правдоподобия
записывается в виде
k |
v |
[(е,Т)=L,ln ле,т)+L,ln(l- F(G,I;'».
j=1 I~
Возьмем производную от данного выражения по искомому параметру
дl(G,Т) = t alnf(G,Tj ) +t aln(l-F(G,I;'»
де j=1 де 1=1 де
и приравняем полученное выражение нулю. Если 8 - вектор порядка k, то необходимо взять k частных производных для получения системы уравнений
при решении которой находим эффективные несмещенные оценки па раметров закона распределения F(8, ().
Рассмотрим примеры оценивания параметров законов распределе
ния.
Экспоненциальное распределение
Запишем функцию распределения F(л., () = 1 - ехр(-Лt) и плотность распределения/(л., () = л.ехр(-л.t) величины (. Пусть требуется опреде-
206
------- ---------------
лить оценку интенсивности отказа с учетом полных и цензурированных
справа наработок. Функция правдоподобия для данного случая пред
ставления информации имеет вид
k |
v |
l(л,t) = L,ln(лехр(-лI;»)+ L,ln (ехр(-лт;)). |
|
;=1 |
j=1 |
Возьмем производную отфункции правдоподобия по параметру л и при
равняем ее нулю:
откуда получаем оценку параметра
).,= k |
k |
v |
L,I; + L,T;
1=1 j=1
Точность определения оценки вычисляется по формуле
).,2
D(л)=т·
Нормальное распределенне
Логарифмическая функция правдоподобия для цензурированной
справа выборки имеет вид
k |
k |
(Т-m)2 |
l(t,moO')=--(ln21t+ln0'2)-'L |
1 2 + |
|
2 |
1=1 |
20' |
v |
[ |
1- |
1 |
т; ( |
х-п: |
)2)] |
+I,ln |
|
~ |
Jexp |
dx. |
||
j=1 |
|
|
V2пО' о |
20' |
|
|
Параметры закона распределения определяются из системы уравнений
al(t,m,O')=_l t(T - m) - _ l - t
дm |
0'2 1=1 I |
.J2iё0' j=1 |
m2 |
) |
(Т;_m)2 |
|
|
ехр -- |
-ехр |
|
|
|
( |
|
20'2 |
|
=0, |
20'2, |
|
|||
1 Ji |
|
(х-m)2 ) |
|
|
T |
ехр |
|
dx |
|
1 --- |
20'2 |
|
||
.J2iё0' о |
|
|
|
|
207

!
I!
1;1
1',
|
1 |
|
(Т)-т)ехр |
(Т;_~)2 +тех |
р |
(- т2 |
) |
|
||
|
v |
|
т' |
2а |
|
2а2 |
|
|
||
+ |
2 ~ |
L |
1 |
|
(Х-т)2 ) |
=0 |
. |
|||
|
2а ,,21Са }=1 |
Ji |
ехр |
|
||||||
|
|
|
1 --- |
|
2а2 |
|
dx |
|
|
|
|
|
|
J2iёa о |
|
|
|
|
|
||
Данная система уравнений является трансцендентной, решается чис
ленными методами. В качестве первого приближения при решении си
стемы можно взять следующие оценки:
k |
k |
~); |
L(1;-тУ |
т 1 =..!::L-, |
a~ =.!.:i-:!..I___ |
k |
k |
Элементы информационной матрицы определяются в виде
а |
11 |
= a2 Z(t,m,cr) =_~+_1_}:в'с-с'в |
|||
|
дт2 |
cr2 |
.J2iCcr j=1 |
С2 , |
|
|
|
|
(Т;_т)2 J (т2 |
) |
|
|
|
|
2а2 |
-ехр -- . |
|
|
|
|
2а2 |
' |
|
, |
Тj,-т |
|
r- |
(}Т'.-т) |
||
В |
=--2-ехр |
|
2а |
2 |
|
|
|
cr |
|
|
|
|
|
|
|
|
1 |
т; |
|
( |
|
С =1--- Jехр |
|
||||
|
|
5а о |
|
|
||
2 J |
т |
( |
т2 |
|
+-ехр |
-- ) . |
|||
|
а2 |
|
2а2 |
' |
(х2-ат2)2)ах;
, |
= |
1 [ |
(т;-т)2) |
(т2)~ |
1 |
|
С |
г;:;-- |
ехр - |
2а2 |
-ехр -- |
= --в· |
|
|
|
,,21Са |
|
2cr2 |
.J2iCcr ' |
|
208
Е' |
= D;F - F;D. D' = (Т;_т)3 |
|
(Т;_т)2) т3 |
(_ т2 ). |
|
jb |
F2' Ь |
2а4 |
ехр |
2а2 + 2а4 ехр |
2а2' |
а = д2 Z(t,т,cr) о.
12дт да2
Вэтом случае ковариация между параметрами а и а2 равна нулю, а дис
персии параметров определяются из выражений
1 |
2 |
1 |
D[m]=--;D[cr |
]=--. |
|
~1 |
|
а22 |
Аналогичные действия выполняются в случае других законов рас пределения случайной величины, отражающей реализацию наблЮдае мого признака. Приведенные примеры иллюстрируюттот факт, что учет цензурированной информации приводит к существенному усложнению
процедуры вычисления параметров рассматриваемого закона распре
деления. Но следует отметить, что сложность решения задачи оцени
вания компенсируется точностью оценок, которую в итоге удается до
стичь за счет учета цензурированной информации.
7.4. Оценивание показателей систем
по группированным данным
в ходе проведения наблюдений за функционированием систем в ряде
случаев исследователь не имеет возможности получать информацию о реализовавшихся значениях наблюдаемой случайной величины. Из
вестными бывают лишь интервалы значений, в которые попал тот или иной результат наблюдения. Наиболее просто и ясно данную ситуацию
иллюстрирует пример с организацией и проведением исследований по
определению характеристик надежности элементов и систем.
14-4355 |
209 |

,1 "
1"
I
Так при решении задачи анализа надежности реально функциониру ющих объектов осуществляется сбор информации о поведении объек тов в процессе их эксплуатации, в частности фиксируются отказы и
соответственно наработки объектов до отказа. Однако в большинстве
случаев доступной является лишь информация о том, что отказы про
изошли в некотором интервале времени. Эro связано с тем, что отказы
устройств фиксируются не мгновенно, а в некоторые, наперед сплани
рованные моменты контроля исправности функционирования оборудо вания или даже в моменты проведения плановых профилактических
работ. Практически мгновенно отказы выявляются унезначительной
группы устройств, имеющих встроенный контроль. В остальных случа ях у исследователя имеется информация о том, что отказ произошел в интервале времени между предыдущим и последующим контролем либо в интервале между очередными профилактиками.
Итак, пусть в системе спланированы моментыI контроля исправно
сти функ-ционирования оборудования ~1' ~2"'" ~k' где О < ~1< ~<...< ~k<
< 00. в моменты контроля выявляется количество отказавших в интер
вале времени [~/-1' ~J устройств, Т.е. наблюдаемыми случайными ве
личинами являются целые неотрицательные числа, характеризующие
количество отказавших объектов на рассматриваемом интервале Nl'
N |
, |
... , Nk+l где N. - |
число устройств, отказавших в интервале [J:.. |
J:..] |
||
J:. 2== О |
J:. |
= 00 ' |
':1'-1' |
':1, , |
||
':10 |
|
|
' ':Ik+l |
- . |
|
|
Данные, представленные таким образом, называются группирован-
ными данными, которые являются частным случаем цензурированных
данных, причем этот случай называется цензурированием интервалом.
Функция правдоподобия в данном случае имеет вид [39]
k+l |
|
L(N1, N 2 , .. ·, Nk+l' е) == П[F(е'~I)- F(e'~i-1)]Ni. |
(7.9) |
Следует обратить особое внимание на граничные точки области оп
ределения параметра ~j' В левой крайней точке ~o = О функция распре деления тождественно равнанулю: F(8,~), поэтому первый член сомно
жителя (7.9) имеет вид
[F(e'~I)- F(e'~o)]N, == [F(e'~I)]NI.
в правой крайней точке ~k+l = 00 функция распределения тождественно
равна единице F(8'~k+I) == 1, поэтому последний член произведения (7.9)
равен
210
Интервал [~k' 00] по своему смыслу представляет собой интервал цен
зурирования справа. В него попадают те элементыI' которые не отказа ли до последнего момента контроля ~k' Предполагается, что далее на
блюдения не проводились, и элементыI' которые не отказали до момен
та ~k' образуютвыборкуцензурированных справа наработок. С учетом'
этого окончательнО функцию правдоподобия можно записать следую-·
щим образом:
це,{N;}) == [F(e'~I)]NIft[F(e'~i+l)- F(e,~)]N + [1- F(e'~k)]N.+ |
• (7.10) |
|
i 1 |
1 |
|
;=1
Прологарифмируем выражение (7.10):
l(e,{N; })==N In F(e'~I)+I,Ni+lln [F(e'~i+l)- F(e,~;)]+Nk+1 In [1- F(e'~k)]:
1
1=1
Решение данного уравнения возможно, как правило, численнымИ мето |
|||
дами: если допустить в последнем уравнении |
Pj(8) = F(8, |
~)- F(8, ~;-1)' |
|
то получим, что оценка максимального правдоподобия |
будет корнем |
||
уравнения правдоподобия |
|
|
|
k+l |
1 д |
|
(7.11) |
LN.--p(e)=o. |
|
||
;=1 |
' ~(e) де ' |
|
|
Покажем процедуру вычисления оценки параметра интенсивнОСТИ
отказа для экспоненциального законараспределения наработки. Функ-,
ция правдоподобия в этом случае будет выглядеть следующим обра7
зом:
i=1
Подставляя в (7.11) РКА.) = ехр(-ц,/_I) - ехр(ц,j)' получаем уравнение
для определения параметра л.экспоненциального закона распределения.
Получить решение данного уравнения можно численными мето~ами. Для приближенного решения может быть применен итеративныи ме
тод Ньютона-Рафсона с начальным значением
'+1 У'
Л, =(6, (= ( "'f..N,t,/n J '
211
14*

;, .1
!
1,
I
,
,
"11,.
",1
,
Как видно из последнего выражения, даже в самом простом слу
чае экспоненциального распределения наработки до отказа параметры
распределения приходится оценивать численными методами. Поэтому можно считать выражение (7.11) окончательным, дальнейшее преоб разование которого нецелесообразно. Процедура оценивания парамет
ров закона распределения реализуется исключительно численными
методами.
7.5. Примеры оценки показателей законов
распределения
в данном параграфе приведем результаты вычисления параметров
законов распределения и определения точности в их оценке для ряда
законов, имеющих наиболее широкое применение в системном анали
зе.
Вначале подведем некоторые итоги. Остановимся еще раз на обо значениях, используемых при расчете показателей:
е - параметр закона распределения; {TJ - реализации наблюдае
мой случайной величины (наработки до отказов); F(e, Т) - функция рас
пределения случайной величины,j(е,Т) - плотность распределения. Функция правдоподобия обозначается через L(e,n, логарифмическая
функция правдоподобия [(е,Т), причем [(е,Т) = ln L(e,n; k - объем вы борки полных наработок, v - количество цензурированныx данных, Т.е.
Тl' Т2,···, Tk - реализации полных и I;~...,т: - цензурированных нарабо
ток.
Для группированных данных имеем следующую информацию: мо
менты контроля исправности функционирования оборудования ~1' ~,••. ,
~k' где О < ~1< ~2<... < ~k <00. В моменты контроля выявляется количе
ство отказавших в интервале времени (~;-1' ~J устройств, т.е. наблюда
емыми случайными величинами являются целые неотрицательные числа, характеризующие количество отказавших объектов на рассмат
риваемом интервале: Nl' N2 , ... , Nk+l; N, - число устройств, отказавших
в интервале (~/-1' ~J Как и ранее функцию правдоподобия для полных
наработок будем писать без индекса
k
L = Пf(е,7;);
;=1
для данных, имеющих наряду с полными цензурированные справа на
работки, будем использовать обозначение
k |
V |
4 = пле,7;)П(l-F(е,Т;»); |
|
;=1 |
j=l |
аналогично, для имеющих цензурированные слева наработки будем
писать
k |
V |
Lл == пле,I;)ПF(e,T;);
1=1 |
j=1 |
для цензурированных интервалом или группированных данных
i=l
После сделанных обозначений приведем результатыI оценивания па раметров законов распределения и оценок дисперсииданных показате-
лей.
Экспоненцнальное распределенне
1. Для полных наработок имеем:
це,Т)= Uеехр(-е7;)= ek ехр(-et7; );
|
k |
|
|
|
д |
klne-e}); |
k |
k |
л k |
дl(е,Т) = |
|
|||
1=1 |
=-- L,7; =0; |
e=-k-' |
||
де |
де |
е |
1=1 |
L,7; |
;=1
Таким образом, в данном случае решение получается в явном виде.
2. Для данных, содержащих полные и цензурированные справа на-
работки:
L,. (6,Т)~Цехр(-6T;)U 6ехр(-6т.)~6' ехр(-еtт;}ХР(-6tТ,}
[(е,Т)= klne-e( t7; +tT;}
al(e,T) =~-(±7;+ f,T;)=O;
де е ;=1 j=1
213
212

!'1
'1,
,111
I
1
,1
1I
Решение так же как и в предыдущем случае получается в явном |
~ = ±N; [~; ехр(-e~)- ~H ехр(-e~H)]. |
||||||||
виде. |
|
|
|
|
|
|
|
||
3. Дляданных, содержащих полные и цензурированные слева нара |
де ;=1 |
ехр(-e~l-l)- ехр(-e~;) |
|||||||
|
|
||||||||
ботки: |
|
|
|
|
|
|
|
Если представить ~/=Ы, ~;.1=~и-l), где ~- временной интервал груп |
|
|
|
|
|
|
|
|
|
||
V |
р |
k |
|
=e |
k |
(k |
lп |
пирования, будем иметь |
|
|
I . |
|
|||||||
Lл(е,Т)=П(1-ех (-ет;)Ч]еехр(-е7;) |
|
ехр -e~7; ~J(I-ехр(-ет;») |
д[ _ ~ N; [Ai(exp(-e~;)-exp(-e~i-1»+Aexp(-e~i-l)] = |
||||||
|
|
|
|
|
|
|
|
||
|
|
k |
V |
|
|
|
|
де - ~ |
ехр(-e~H)- ехр(-e~;) |
|
[(е,Т) = kln e-еL,7; + L,ln(l-exp(-ет;)} |
|
|
||||||
/-1 j=1
|
|
|
д[ЩТ) =!_ :i); + i |
Т;ехр(-ет;) = |
|
|
|||||
|
|
|
де |
е |
;=1 |
j=1 l-exp(-етj) |
|
|
|
||
k |
k |
v T~(I-exp(-eT~))-T~ |
k |
k |
k |
v |
т' |
,=0. |
|||
=--L,I;-L, J |
|
J, |
J |
=--L,7;-L,T;+L, |
j |
||||||
е |
;=1 |
j=1 |
1- ехр(-еТj |
) |
е |
;=1 |
j=1 |
j=1 |
1- ехр(-еТj) |
||
Данное уравнение в явном виде не имеетпредставления. Программ
ная реализация решения подобных уравнений требует применения чис
ленных методов.
4. В случае, когда выборка содержит только группированные дан
ные, решение имеет следующий вид:
k+l
Lг(Nl'N2,···,Nk+1,e) = П[F(G,~)- F(e'~i-1)]N.;
;=1
k
t; NJ =
|
~ |
. ~ |
Aexp(-e~l-l) |
_ о. |
|
|
=-~NАl+ ~ |
|
- , |
|
|
|
;=1' |
;=1 |
ехр(-e~H) - ехр(-e~i) |
|
|
k |
exp(-e~ ) |
± |
exp(-M(i-l» |
. |
|
~ехр(-e~H) |
- ~~~(-e~i) = ;=1 ехр(-M(i -1»[1- ехр(-М)]' |
||||
|
k |
k |
1 |
k |
|
|
~NJ=t;I-еХР(-М) =1-ехр(-М); |
|
|||
е=-1n l-уtNJ
А
Приведем результаты определения точности оценки параметра
экспоненциального закона распределения.
Дисперсионная матрица для вектора параметров определяется пу:
k+l |
k+l |
[= lnLг = L,N; ln[F(e,~)- F(е'~I-l)]= L,N; ln[exp(-e~i-l)-exp(-e~)]; |
|
1=1 |
1=1 |
~=rN, [~i-l ехр(-e~/_I)-~; ехр(-e~;)] =о. |
|
де ;=1 |
ехр(-e~H) - ехр(-e~;) |
Приравныхинтервалахцензурированиярешениеможнопредставить
в следующем виде:
k
Lг(N1,N2 ,···, Nk , е) =П[exp(~H)-exp(e~;)]N.;
1-1
k
[=L, N; 1n [ехр(-e~H)- ехр(-e~;)];
1=1
тем транспонирования информационной матрицы, элементы которои
имеют вид
в нашем случае оценки одного параметра необходимо определить вто
рую производную по параметру:
-1 |
д2 [ |
D |
=- де2 • |
214 |
215 |
|
I
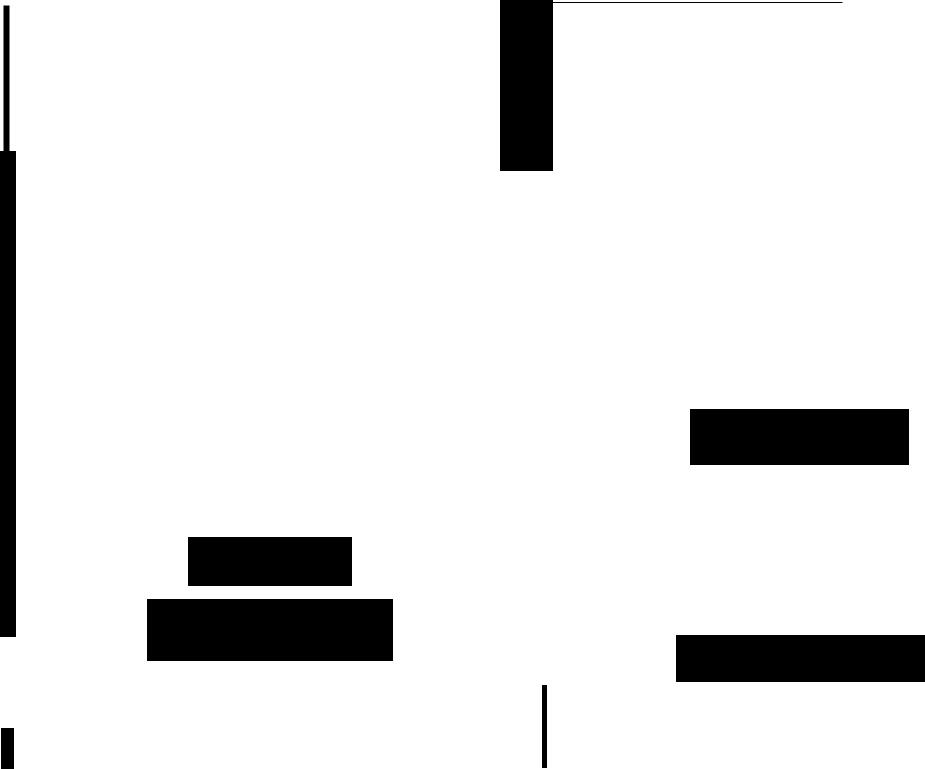
Витоге будем иметь следующие результаты.
1.для полных наработок:
k
|
|
|
|
д klne-e~); |
|
|
|
|
|
|
_al....:..(e...:....T~), = ---"-__--"",;;.=I---L = ! _±,т. |
|
|
||||
|
|
де |
|
де |
е |
'=1 l' |
|
|
|
|
D-1 =_ a1 =_(_~). D= f)2 |
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
де2 |
f)2' |
k . |
|
|
2. для выборки, содержащей полные и цензурированные справа нара |
||||||||
ботки: |
|
|
|
|
|
|
|
|
al(e,T) = !_(~т+ ~Т')=О' D-1 = _~=_(_ k ). D= f)2 |
||||||||
де |
е |
f:t I |
f:t |
J' |
де2 |
ет |
' |
k . |
3. для выборки, содержащей полные и цензурированные слева на |
||||||||
работки: |
|
|
|
|
|
|
|
|
|
al(e,n =!_ ±,т _tT~+ t т;ехр(-ет;). |
|
|
|||||
|
|
де |
е |
/=1 I /=1 |
J j=1 1- ехр(-ет;), |
|
|
|
a1(e,n =_.!:.+ t -(T;)2exp(-6T;)(1-exp(~T;))-17exp(-eT;)T;exp(-eT;) = |
||
2 |
|
|
(ю2 |
Ef j=1 |
(l-exp(~T;))2 |
=_.!:.+ t _(т;)2ехр(-ет;)+(т;)2ехр(-2ет;)-(т;)2ехр(-2ет;)= |
||
е2 |
j=1 |
(l-ехр(-ет;))2 |
4. для группированных данных:
~ = ±, N; [~; ехр(-e~,)- ~'-1 ехр(-e~H)];
де '=1 exp(-~'_I)-exp(-e~)
a21 =± |
1 |
2[N'(~:_lеХр(-е~'_I)-~/ехр(-е~,))х |
де2 ;=1 |
[exp(-e~H)-exp(-e~;)] |
|
x(exp(-e~H)-exp(-e~,))-(~; exp(-e~,)-~I-lexp(-e~H))X |
||
|
x(~, exp(-е~I)-~'_1exp(-e~i-l))= |
|
= ±, |
N, |
2 [~_lexp(-2e!;_I)+C/exp(-2e!;)-c/exp(~~+~_I)- |
'=1 [ехр(--е1;.·-I)- ехр(---е1;)] |
|
|
--{) ехр(~(~+~-1))-[~ехр(-2е!;)+~)ехр(-2е!;_1)- ~-1~ехр(~(~+~-I))]]= |
||
|
== ±N exp(-e(~; +~'-1»)(-1)(~, -~-1)2. |
|
|
;=1 I |
[ехр(-e~'_I)- ехр(-e~)] |
в случае равных интервалов группирования:
~=_~ N,Ai+ ± |
|
Аех~(-GA(i-l)) . |
=-±,N,Ai+А± |
1 |
; |
||||
де |
f:t |
'=1 exp(-еА(l-l))-ехр(-еAi) |
'=1 |
;-1 [l-exp(-GA)] |
|
||||
|
|
a21 |
2± |
exp(-еА) . D-,/[A2 ± exp(-f)А) |
] |
|
|||
|
|
де2 =-А |
;=1 |
[1-ехр(-еА)]2' |
-7 |
;Cl[1-exp(-GA)]2' |
|
||
имеем в виду, что:
216 |
217 |
|
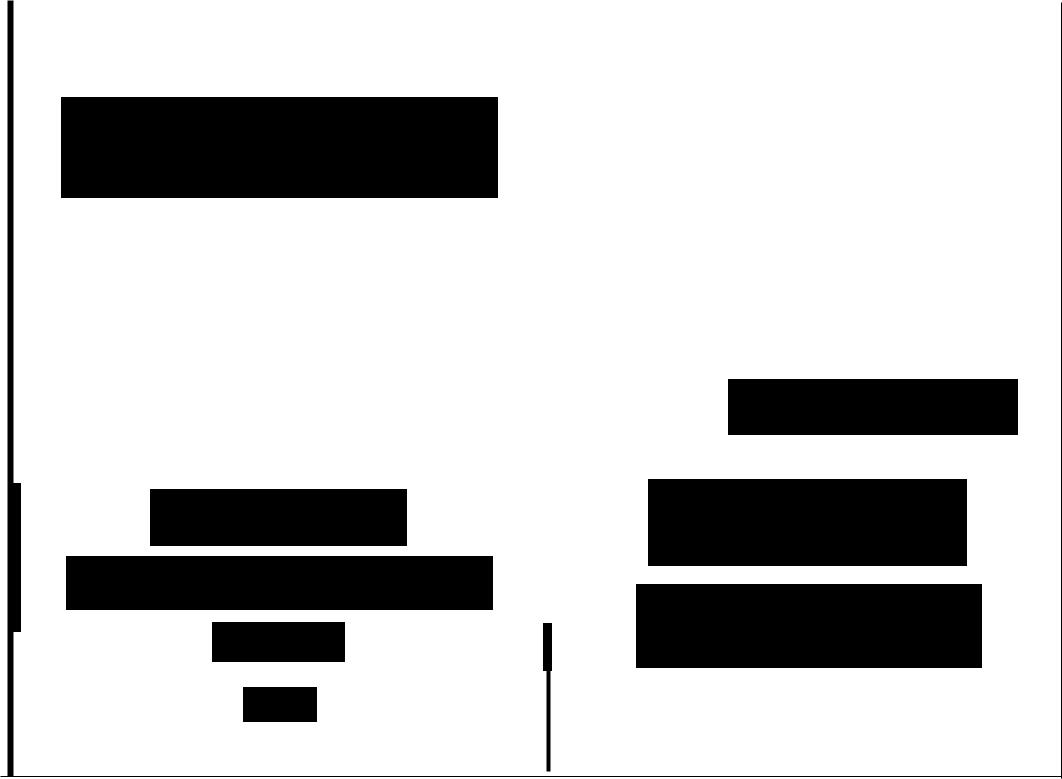
1,
J, .
тогда: |
I ~.~' |
Нормальное распределение |
|
|
||
Плотность и функция распределения для нормального закона рас |
||||
пределения имеют вид: |
|
|
|
|
I |
|
r (t-m)21 |
||
!(t,m,o) = |
1 |
|||
~exp |
|
2; |
||
I!I |
Оу2п |
|
20 |
|
~!exi - (X-7)2 Idx. |
||||
F(t,m,o) = |
||||
ov2n _ |
l |
20 J |
||
в данных формулах приняты обозначения: т - математическое ожида |
||||
ние; (j - среднее квадратическое отклонение. При получении оценок |
||||
параметров и определении точности в их оценке будем также в каче
стве математического ожидания использовать обозначение 81'в каче стве среднего квадратического отклонения - 82'Приведем результаты вычислений.
1. В случае полных наработок имеем:
откуда получаем
218
i
I
!
Производя аналогичные действия для второго параметра, получим
~=_~+ke~-2el}); +});2 =0;
де2 |
е2 |
|
e~ |
ke~ =ke~ -2el~); +});2 = L(7; -( )2 |
|||
|
|
|
1 |
в итоге получаем следующую формулу |
|||
|
л |
1 k |
л |
|
e~ =- L(7; -(1)2. |
||
|
|
k 1=1 |
|
2. для выборок, содержащих полные и цензурированные справа на |
|||
работки, функция правдоподобия имеет вид |
|||
Ln (ере2, |
1 |
ехр |
( t (1; - е/] |
у ( т. 1 |
ехр |
( (1 -е/))dl' |
{7;} ) = (J2;r.eJ |
;.1 2e~ |
U1-1J2;r.e |
2e~ |
2
логарифмическая функция правдоподобия:
k
1= --ln(21t)- k lne2
2
и, наконец, частные производные определяются выражениями
в данном случае результar в явном виде получить не удается, поэтому
необходимо решать трансцендентные уравнения.
219
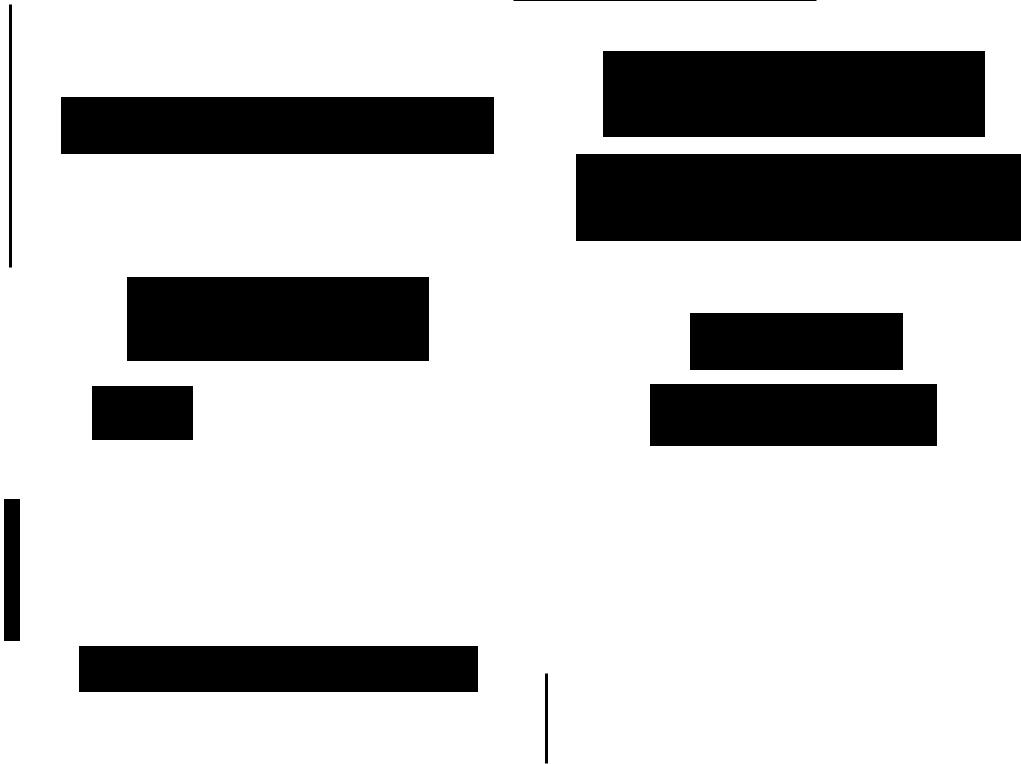
3. Для выборок, содержащих полные и цензурированные слева на
работки, функция правдоподобия записывается
логарифмическая функция правдоподобия:
k |
L, (Т - G )2 |
v |
т, |
1 |
ехр |
(t G i ) |
|
1=lnl=--(ln21t+lnG~)- |
; 2 ' |
+ L,ln J ~ |
- - ; |
dt; |
|||
2 |
2е2 |
j=' |
_ |
,<,2пе2 |
|
2е2 |
|
частные производные:
k |
|
1 |
(Т'- е, )2 |
, |
|
'f- Бе~ ехр - |
J 2e~ (T |
-е,) |
|||
|
|
|
|
j |
|
-+ k |
т' |
(t -е,)2 ) |
=0. |
||
е2 |
j=' |
J' 1 |
dt |
||
|
|
--ехр - |
|
||
· I |
|
_Бе2 |
|
2e~ |
|
Для выборок, содержащих цензурированные слева наработки, де
лаем тот же вывод, что и в предыдущем случае, а именно, решение
необходимо искать численными методами.
4. для группированных данных итоговые оценки получаются таким образом. Функция правдоподобия:
4(G"G ,{I;})= fIrTJ |
~ exi- (t-G;)2 Idt _ J ~ exi_ (t-G;)2IdtlNi; |
2 |
,<,2пе2 l 2е2 ) _ ,<,2пе2 l 2е2 ) |
;=, - |
логарифмическая функция правдоподобия:
производные от нее по параметрам:
220
,
,.
Рассмотрим вопрос вычисления точности в полученных оценках. Определим вторые производные для случая, Korдa имеются в наличии
полные наработки.
|
k |
л |
|
1 |
L,(I; _е,)2 |
k |
|
-3 .=, |
4 |
+ |
2' |
-- |
|
||
De, |
е2 |
|
е2 |
Для всех остальных типов данных при расчете дисперсии получа
ются результаты, не имеющие представления в явном виде. Поиск ре
шения осуществляется численными методами, поэтому итоговые фор
мулы не приводятся.
Усеченное нормальное распределенне
Плотность усеченного нормального распределения имеет следую
щийвид:
{ |
С |
(х-m)2) |
х>О; |
|
|
--ехр |
2а |
2' |
|
j(x) = ~~О, |
|
|
||
221
