
matan_vse_k_ekzamenu_za_1_semestr
.docx
Комплексные
числа (определение, примеры). Два
вещественных числа x
и y
будем называть упорядоченной парой,
если указано, какое из этих чисел является
первым, какое вторым. Тогда комплексным
числом z
называется упорядоченная пара (x,
y)
вещественных чисел, первое из которых
x
называется действительной частью, а
второе y
– мнимой частью этого комплексного
числа. Записывается комплексное число
в виде выражения: z
= x
+ iy.
Символ
i
носит название мнимой единицы и
определяется соотношением i2
= -1.
Примеры: z
= 1+3i; z = -4i; z = (2-i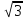 )45.
)45.
Сложение,
вычитание, умножение и деление комплексных
чисел.
Суммой двух комплексных чисел z1
= (x1,
y1)
и z2
= (x2,
y2)
назовём комплексное число z
вида z
= (x1+x2,
y1+y2)
или z
= z1+z2
= (x1+x2)+i(y1+y2).
Разностью двух комплексных чисел z1
= (x1,
y1)
и z2
= (x2,
y2)
называется такое комплексное число z,
которое в сумме с z2
даёт z1
и записывается в виде z
= (x1-x2,
y1-y2)
или z
= z1-z2
= (x1-x2)+i(y1-y2).
Произведением двух комплексных чисел
z1
= (x1,
y1)
и z2
= (x2,
y2)
назовём комплексное число z
вида z
= (x1x2-y1y2,
x1y2+x2y1)
или z
= (x1x2-y1y2)+i(x1y2+x2y1).
Частным двух комплексных чисел z1
= (x1,
y1)
и z2
= (x2,
y2),
второе из которых не равно нулю, называется
такое комплексное число z,
которое при умножении на z2
даёт z1
и записывается в виде z
=
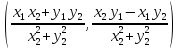 или z
=
или z
=
 =
=
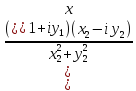 .
.
Комплексно-сопряженное
число. Комплексное
число
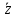 =
(x,
–y)
= x-iy
принято называть сопряжённым по отношению
к комплексному числу z
= (x,
y)
= x+iy.
=
(x,
–y)
= x-iy
принято называть сопряжённым по отношению
к комплексному числу z
= (x,
y)
= x+iy.
Геометрическое
представление комплексного числа.
Геометрически комплексное число z
= (x,
y)
представляется
в виде точки
M
или
радиус-вектора
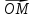 в плоскости, называемой комплексной
плоскостью. В декартовой системе
координат точка M
и
в плоскости, называемой комплексной
плоскостью. В декартовой системе
координат точка M
и
 имеют координаты (x,
y).
имеют координаты (x,
y).
Тригонометрическая
и показательная формы записи комплексного
числа. Если
наряду с декартовой системой координат
ввести полярную, причём так, чтобы полюс
находился в начале O
декартовой
системы, а полярная ось была направлена
вдоль положительного направления оси
Ox,
то декартовы координаты (x,
y)
и полярные координаты (ρ,
φ)
любой точки M,
как известно, связаны формулами ρ
=
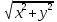 ;
x
= ρ∙cos
φ; y
= ρ∙sin
φ; tg
φ =
;
x
= ρ∙cos
φ; y
= ρ∙sin
φ; tg
φ =
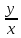 .
Число z
= (x,
y)
представляется в тригонометрической
форме как z
= x
+ iy
= (ρ∙cos
φ, ρ∙sin
φ) = ρ(cos
φ+i∙sin
φ),
где число ρ
называют модулем, а угол φ
аргументом комплексного числа, причём
вместо значения φ
можно брать значение
φ+2πn
, где
n
= 0,±1, ±2, …
Исходя из формулы Эйлера в показательной
форме комплексное число представляется
как z
= ρ∙
.
Число z
= (x,
y)
представляется в тригонометрической
форме как z
= x
+ iy
= (ρ∙cos
φ, ρ∙sin
φ) = ρ(cos
φ+i∙sin
φ),
где число ρ
называют модулем, а угол φ
аргументом комплексного числа, причём
вместо значения φ
можно брать значение
φ+2πn
, где
n
= 0,±1, ±2, …
Исходя из формулы Эйлера в показательной
форме комплексное число представляется
как z
= ρ∙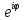 .
.
Формула
Эйлера. Формула
Эйлера представляется в виде выражения
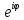 =
cos
φ+i∙sin
φ.
=
cos
φ+i∙sin
φ.
Возведение
в степень и извлечение корней из
комплексных чисел. Если
перемножаются n
равных комплексных чисел, т.е. если
комплексное число возводится в степень
n,
то zn
= (ρ∙cos
φ, ρ∙sin
φ)n
= (ρ∙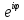 )n
= ρn∙
)n
= ρn∙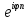 =
=
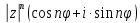 .
Извлечение корня степени n
– обратная операция возведению в степень
n,
поэтому
.
Извлечение корня степени n
– обратная операция возведению в степень
n,
поэтому
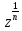 =
=
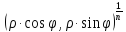 =
=
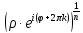 =
=
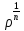 ∙
∙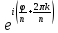 =
=
 ,
где
,
где
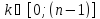 .
.
Числовые
последовательности (определение,
ограниченные, неограниченные, бесконечно
большие и бесконечно малые). Будем
ставить в соответствии числу n
из натурального ряда 1,2,3,…,n,…
некоторое вещественное число xn
по заданному закону. Тогда множество
x1,x2,x3,…,xn,…
пронумерованных чисел называется
числовой последовательностью.
Последовательность
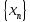 называется ограниченной сверху (снизу)
числом M
(числом m),
если каждый элемент этой последовательности
удовлетворяет неравенству
называется ограниченной сверху (снизу)
числом M
(числом m),
если каждый элемент этой последовательности
удовлетворяет неравенству
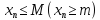 .
Число M
(число m)
называется верхней (нижней) гранью
числовой последовательности.
Последовательность
.
Число M
(число m)
называется верхней (нижней) гранью
числовой последовательности.
Последовательность
 называется ограниченной с обеих сторон,
если она ограничена сверху числом M,
а
снизу числом m,т.е.
каждый элемент этой последовательности
удовлетворяет неравенству
называется ограниченной с обеих сторон,
если она ограничена сверху числом M,
а
снизу числом m,т.е.
каждый элемент этой последовательности
удовлетворяет неравенству
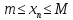 .
Последовательность, ограниченная со
всех сторон, называется ограниченной
последовательностью. Последовательность
.
Последовательность, ограниченная со
всех сторон, называется ограниченной
последовательностью. Последовательность
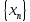 называется неограниченной, если для
любого сколько угодно большого числа
называется неограниченной, если для
любого сколько угодно большого числа
 найдётся хотя бы один элемент
найдётся хотя бы один элемент
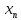 последовательности, для которого
выполняется неравенство
последовательности, для которого
выполняется неравенство
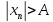 .
Последовательность
.
Последовательность
 называется бесконечно большой, если
для любого сколько угодно большого
называется бесконечно большой, если
для любого сколько угодно большого
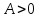 найдётся номер N
= N(A)
такой, что при
найдётся номер N
= N(A)
такой, что при
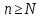 выполняется неравенство
выполняется неравенство
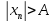 .
Последовательность
.
Последовательность
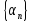 называется бесконечно малой, если для
любого сколько угодно малого
называется бесконечно малой, если для
любого сколько угодно малого
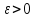 найдётся номер N
= N(ε)
такой, что при
найдётся номер N
= N(ε)
такой, что при
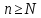 выполняется неравенство
выполняется неравенство
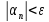 .
.
Арифметические
действия с числовыми последовательностями.
Рассмотрим две последовательности
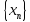 и
и
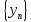 .
Суммой двух последовательностей
.
Суммой двух последовательностей
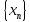 и
и
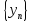 называется последовательность
называется последовательность
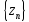 ,
элементы которой равны z1
= x1+y1,
z2
= x2+y2,…,zn
= xn+yn,…
Разностью двух последовательностей
,
элементы которой равны z1
= x1+y1,
z2
= x2+y2,…,zn
= xn+yn,…
Разностью двух последовательностей
 и
и
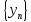 называется последовательность
называется последовательность
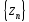 ,
элементы которой равны z1
= x1-y1,
z2
= x2-y2,…,zn
= xn-yn,…
Произведением двух последовательностей
,
элементы которой равны z1
= x1-y1,
z2
= x2-y2,…,zn
= xn-yn,…
Произведением двух последовательностей
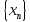 и
и
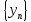 называется последовательность
называется последовательность
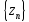 ,
элементы которой равны z1
= x1∙y1,
z2
= x2∙y2,…,zn
= xn∙yn,…
Частным
двух последовательностей
,
элементы которой равны z1
= x1∙y1,
z2
= x2∙y2,…,zn
= xn∙yn,…
Частным
двух последовательностей
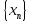 и
и
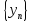 называется последовательность
называется последовательность
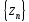 ,
элементы которой равны z1
= x1/y1,
z2
= x2/y2,…,zn
= xn/yn,…
,
элементы которой равны z1
= x1/y1,
z2
= x2/y2,…,zn
= xn/yn,…
Теорема
1:
Сумма двух бесконечно малых
последовательностей
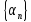 и
и
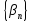 есть бесконечно малая последовательность.
Доказательство:
Обозначим
сумму последовательностей как
есть бесконечно малая последовательность.
Доказательство:
Обозначим
сумму последовательностей как
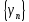 ,
т.е.
,
т.е.
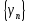 =
=
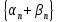 .
Т.к.
.
Т.к.
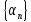 является бесконечно малой последовательностью,
то для любого
является бесконечно малой последовательностью,
то для любого
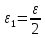 найдётся номер N1
такой, что выполняется
найдётся номер N1
такой, что выполняется
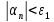 ,
при
,
при
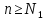 .
Аналогично и для
.
Аналогично и для
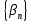 .
Для любого
.
Для любого
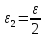 найдётся номер N2
такой, что выполняется
найдётся номер N2
такой, что выполняется
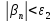 ,
при
,
при
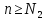 .
Обозначим через N
= max{N1;N2}.
Оценим
.
Обозначим через N
= max{N1;N2}.
Оценим
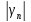 при
при
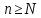 .
.
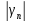 =
=
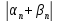 ≤
≤
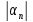 +
+
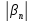 < ε1
+ ε2
=
< ε1
+ ε2
=
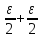 = ε.
= ε.
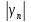 < ε,
ч.т.д.
< ε,
ч.т.д.
Теорема
2:
Разность двух бесконечно малых
последовательностей
 и
и
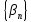 есть бесконечно малая последовательность.
Доказательство: аналогично доказательству
теоремы 1 с использованием свойства
есть бесконечно малая последовательность.
Доказательство: аналогично доказательству
теоремы 1 с использованием свойства
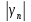 =
=
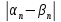 ≤
≤
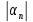 +
+
 .
Следствие:
Любая алгебраическая сумма конечного
числа бесконечно малой последовательности
есть бесконечно малая последовательность.
.
Следствие:
Любая алгебраическая сумма конечного
числа бесконечно малой последовательности
есть бесконечно малая последовательность.
Теорема
3:
Бесконечно малая последовательность
является ограниченной. Доказательство:
Рассмотрим последовательность
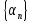 .
В соответствии с определением для любого
.
В соответствии с определением для любого
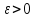 найдётся номер N
= N(ε)
такой, что при
найдётся номер N
= N(ε)
такой, что при
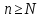 выполняется неравенство
выполняется неравенство
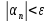 .
.
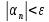 ;
;
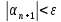 ;…
Получается
;…
Получается
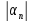 ,
,
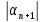 ,
…, ε.
Тогда max{
,
…, ε.
Тогда max{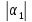 ,
,
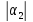 ,
…,
,
…,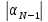 ,
ε}
= A,
а для всех n
выполняется
,
ε}
= A,
а для всех n
выполняется
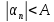 ,
таким образом, получили, что
,
таким образом, получили, что
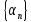 ограничена, ч.т.д.
ограничена, ч.т.д.
Теорема
4:
Произведение бесконечно малой
последовательности
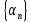 на ограниченную
на ограниченную
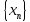 есть бесконечно малая последовательность.
Доказательство:
Т.к.
есть бесконечно малая последовательность.
Доказательство:
Т.к.
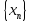 ограниченная последовательность, то
должно выполняться
ограниченная последовательность, то
должно выполняться
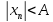 .
Для бесконечно малой последовательности
для любого
.
Для бесконечно малой последовательности
для любого
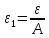 найдётся номер N,
такой, что выполняется
найдётся номер N,
такой, что выполняется
 .
Проведём оценку элементов произведения
последовательностей
.
Проведём оценку элементов произведения
последовательностей
 ·
·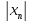 =
=
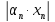 <
<
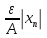 <
<
 ·A
= ε, следовательно
·A
= ε, следовательно
 < ε при
< ε при
 ,
а следовательно
,
а следовательно
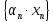 бесконечно малая, ч.т.д. Следствие:
Произведение конечного числа бесконечно
малых последовательностей есть бесконечно
малая последовательность.
бесконечно малая, ч.т.д. Следствие:
Произведение конечного числа бесконечно
малых последовательностей есть бесконечно
малая последовательность.
Теорема
5:
Если все элементы бесконечно малой
последовательности
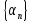 равны одному и тому же числу C,
то C=0.
Доказательство:
По условию теоремы
равны одному и тому же числу C,
то C=0.
Доказательство:
По условию теоремы
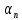 = C,
где n
= 1,2,3…
Предположим, что C
≠ 0. Тогда величину
= C,
где n
= 1,2,3…
Предположим, что C
≠ 0. Тогда величину
 > 0
можно принять за ε, т.е. выбрать ε =
> 0
можно принять за ε, т.е. выбрать ε =
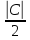 .
По определению для этого ε должно найтись
число N(ε)
такое,
что выполняется неравенство
.
По определению для этого ε должно найтись
число N(ε)
такое,
что выполняется неравенство
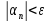 ,
а следовательно
,
а следовательно
 ,
что равносильно неверному неравенству
1
<
,
что равносильно неверному неравенству
1
<
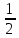 ,
следовательно предположение неверно.
Таким образом C
= 0,
ч.т.д.
,
следовательно предположение неверно.
Таким образом C
= 0,
ч.т.д.
Теорема
6:
Пусть
 есть бесконечно большая последовательность,
тогда начиная с некоторого номера N*
определена последовательность
есть бесконечно большая последовательность,
тогда начиная с некоторого номера N*
определена последовательность
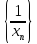 ,
которая является бесконечно малой.
Пусть
,
которая является бесконечно малой.
Пусть
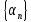 бесконечно малая последовательность,
все элементы которой отличны от нуля.
Тогда последовательность
бесконечно малая последовательность,
все элементы которой отличны от нуля.
Тогда последовательность
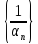 есть бесконечно большая последовательность.
Доказательство:
Т.к.
есть бесконечно большая последовательность.
Доказательство:
Т.к.
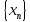 есть бесконечно большая последовательность,
то в соответствии с определением для
любого
есть бесконечно большая последовательность,
то в соответствии с определением для
любого
 найдётся номер N*
такой, что при
найдётся номер N*
такой, что при
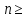 N*
выполняется неравенство
N*
выполняется неравенство
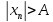 .
.
 > 0,
> 0,
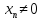 при
при
 N*.
Следовательно определена последовательность
N*.
Следовательно определена последовательность
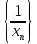 .
Выберем теперь
.
Выберем теперь
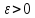 .
Возьмём
.
Возьмём
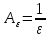 .
Поскольку
.
Поскольку
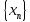 бесконечно большая последовательность,
то
бесконечно большая последовательность,
то
 при
при
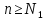 .
Оценим элементы последовательности
.
Оценим элементы последовательности
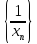 при
при
 .
.
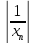 =
=
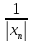 <
<
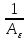 = ε.
Следовательно
= ε.
Следовательно
 < ε
при
< ε
при
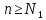 ,
а значит
,
а значит
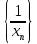 является бесконечно малой, ч.т.д.
является бесконечно малой, ч.т.д.
Сходящаяся последовательность и её предел (два определения).
1)
Последовательность
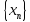 называется сходящейся к числу a,
если последовательность
называется сходящейся к числу a,
если последовательность
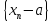 является бесконечно малой, т.е.
является бесконечно малой, т.е.
 =
=
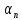 .
Число a
называется пределом последовательности
.
Число a
называется пределом последовательности
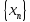 .
.
2)
Последовательность
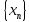 называется сходящейся к числу a,
если для любого
называется сходящейся к числу a,
если для любого
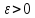 найдётся номер N
= N(ε)
такой, что при
найдётся номер N
= N(ε)
такой, что при
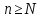 выполняется неравенство
выполняется неравенство
 .
.
Теорема
7:
Сходящаяся последовательность имеет
единственный предел. Доказательство:
Пусть
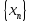 сходящаяся
последовательность. Предположим, что
она имеет два предела a
и b.
Тогда справедливо, что
сходящаяся
последовательность. Предположим, что
она имеет два предела a
и b.
Тогда справедливо, что
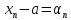 ;
;
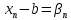 и b
– a
=
и b
– a
=
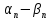 =
=
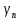 .
Тогда в соответствии с теоремой 5 (если
все элементы бесконечно малой
последовательности
.
Тогда в соответствии с теоремой 5 (если
все элементы бесконечно малой
последовательности
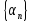 равны одному и тому же числу C,
то C=0)
получим, что b
– a
= 0, а значит b
= a,
ч.т.д.
равны одному и тому же числу C,
то C=0)
получим, что b
– a
= 0, а значит b
= a,
ч.т.д.
Теорема
8:
Сходящаяся
последовательность ограничена.
Доказательство:
Пусть
 сходящаяся
к a
последовательность. Тогда справедливо
равенство
сходящаяся
к a
последовательность. Тогда справедливо
равенство
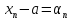 =>
=>
 ;
;
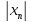 =
=
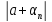 ≤
≤
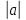 +
+
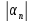 <
<
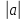 + A1
= A
(т.к.
+ A1
= A
(т.к.
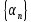 - ограничена). Итак,
- ограничена). Итак,
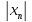 < A,
следовательно последовательность
< A,
следовательно последовательность
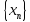 - ограничена, ч.т.д.
- ограничена, ч.т.д.
Теорема
9:
Сумма
двух сходящихся последовательностей
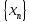 и
и
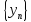 есть сходящаяся последовательность,
предел которой равен сумме пределов
последовательностей
есть сходящаяся последовательность,
предел которой равен сумме пределов
последовательностей
 и
и
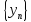 .
Доказательство:
Т.к.
.
Доказательство:
Т.к.
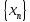 и
и
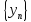 сходящиеся последовательности, то
справедливы следующие равенства:
сходящиеся последовательности, то
справедливы следующие равенства:
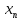 + a
=
+ a
=
 и
и
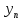 + b
=
+ b
=
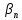 .
Сложив данные равенства получим, что
.
Сложив данные равенства получим, что
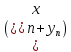 –
(a
+ b)
=
–
(a
+ b)
=
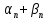 =
=
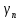 ,
таким образом, последовательность
,
таким образом, последовательность
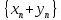 сходящаяся и её предел равен
сходящаяся и её предел равен
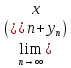 =
=
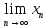 +
+
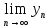 = a
+ b,
ч.т.д.
= a
+ b,
ч.т.д.
Теорема
10:
Разность
двух сходящихся последовательностей
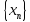 и
и
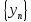 есть сходящаяся последовательность,
предел которой равен разности пределов
последовательностей
есть сходящаяся последовательность,
предел которой равен разности пределов
последовательностей
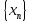 и
и
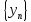 .
Теорема
11:
Произведение двух сходящихся
последовательностей
.
Теорема
11:
Произведение двух сходящихся
последовательностей
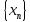 и
и
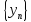 есть сходящаяся последовательность,
предел которой равен произведению
пределов последовательностей
есть сходящаяся последовательность,
предел которой равен произведению
пределов последовательностей
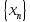 и
и
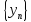 .
Доказательство:
Т.к.
.
Доказательство:
Т.к.
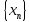 и
и
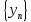 сходящиеся последовательности, то
справедливы следующие равенства:
сходящиеся последовательности, то
справедливы следующие равенства:
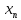 = a
+
= a
+
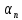 и
и
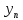 = b
+
= b
+
 .
Перемножив данные равенства получим,
что
.
Перемножив данные равенства получим,
что
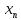 ·
· = (a
+
= (a
+
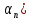 (
b
+
(
b
+
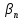 )
=
)
=
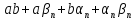 =
=
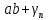 ,т.е.
,т.е.
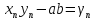 ,
таким образом, последовательность
,
таким образом, последовательность
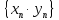 сходящаяся и её предел равен
сходящаяся и её предел равен
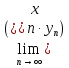 =
=
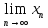 ·
·
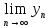 = a
· b,
ч.т.д.
= a
· b,
ч.т.д.
Лемма
1:
Пусть
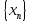 сходящаяся последовательность, предел
которой отличен от нуля. Тогда
последовательность
сходящаяся последовательность, предел
которой отличен от нуля. Тогда
последовательность
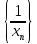 ограничена. Доказательство:
Пусть
ограничена. Доказательство:
Пусть
 сходится к числу b≠0,
тогда ε
=
сходится к числу b≠0,
тогда ε
=
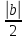 > 0.
Для этого ε
найдётся номер N(ε)
такой, что
> 0.
Для этого ε
найдётся номер N(ε)
такой, что
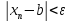 =
=
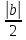 .
Оценим величину
.
Оценим величину
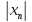 и запишем тождество: b
=
и запишем тождество: b
=
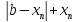 =>
=>
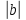 ≤
≤
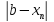 +
+
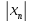 <
<
 ,
при n
≥ N(ε)
=>
,
при n
≥ N(ε)
=>
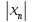 >
>
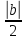 > 0;
> 0;
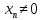 .
Тогда можно образовать последовательность
.
Тогда можно образовать последовательность
 при n
> N(ε).
при n
> N(ε).
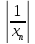 =
=
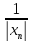 <
<
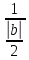 =
=
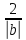 > 0;
> 0;
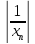 <
<
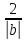 ,
таким образом, последовательность
,
таким образом, последовательность
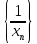 ограничена, ч.т.д.
ограничена, ч.т.д.
Теорема
12:
Частное двух сходящихся последовательностей
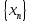 и
и
 ,
при условии, что предел последовательности
,
при условии, что предел последовательности
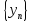 отличен от нуля, есть сходящаяся
последовательность, предел которой
равен частному пределов последовательностей
отличен от нуля, есть сходящаяся
последовательность, предел которой
равен частному пределов последовательностей
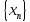 и
и
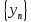 .
Доказательство:
Пусть
.
Доказательство:
Пусть
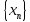 сходится к числу a,
а последовательность
сходится к числу a,
а последовательность
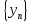 к числу b.Надо
доказать, что последовательность
к числу b.Надо
доказать, что последовательность
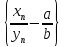 есть бесконечно малая последовательность.
есть бесконечно малая последовательность.
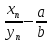 =
=
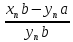 =
=
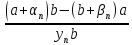 =
=
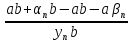 =
=
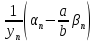 =
=
 ,
таким образом
,
таким образом
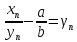 ,
т.е. последовательность
,
т.е. последовательность
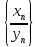 сходится, ч.т.д.
сходится, ч.т.д.
Теорема
13.
Пусть
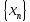 сходится к числу a,
и пусть начиная с некоторого номера
выполняется неравенство
сходится к числу a,
и пусть начиная с некоторого номера
выполняется неравенство
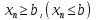 ,
тогда и для предельного значения
a
справедливо аналогичное неравенство
,
тогда и для предельного значения
a
справедливо аналогичное неравенство
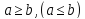 .
Доказательство:
Докажем для случая
.
Доказательство:
Докажем для случая
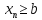 .
Для предела a
могут быть справедливы неравенства
.
Для предела a
могут быть справедливы неравенства
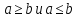 .
Предположим выполнение
.
Предположим выполнение
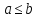 ,
тогда b
> a
=> b
– a
> 0.
Выберем ε
= b
– a.
Для этого
ε
в силу сходимости
,
тогда b
> a
=> b
– a
> 0.
Выберем ε
= b
– a.
Для этого
ε
в силу сходимости
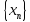 найдётся номер N(ε)
такой, что
найдётся номер N(ε)
такой, что
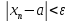 = b
– a
=> –(b
– a)
<
= b
– a
=> –(b
– a)
<
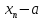 < b
– a;
< b
– a;
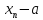 < b
– a
=>
< b
– a
=>
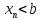 ,
но это противоречит условию
,
но это противоречит условию
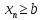 теоремы . Значит наше предположение
неверно, а верно
теоремы . Значит наше предположение
неверно, а верно
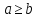 ,
ч.т.д. Следствие
1:
Пусть
,
ч.т.д. Следствие
1:
Пусть
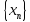 и
и
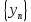 есть сходящиеся последовательности и
пусть начиная с некоторого номера
выполняется неравенство
есть сходящиеся последовательности и
пусть начиная с некоторого номера
выполняется неравенство
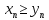 .
Тогда и для пределов этих последовательностей
выполняется неравенство
.
Тогда и для пределов этих последовательностей
выполняется неравенство
 =
=
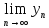 .
Следствие
2:
Если все элементы сходящейся
последовательности
.
Следствие
2:
Если все элементы сходящейся
последовательности
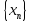 принадлежат сегменту [c,
d],
то и предел a
этой последовательности принадлежит
[c,
d].
принадлежат сегменту [c,
d],
то и предел a
этой последовательности принадлежит
[c,
d].
