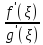matan_vse_k_ekzamenu_za_1_semestr
.docx
Возрастание и убывание функции в точке.
Определение:
функция y=f(x)
возрастает (убывает) в точке
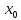 ,
если найдется такая окрестность точки
,
если найдется такая окрестность точки
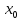 ,
что выполняется: f(x)>f(
,
что выполняется: f(x)>f( )
(f(x)<f(
)
(f(x)<f(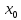 ))при
x>
))при
x>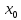 ;f(x)<f(
;f(x)<f(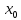 )
(f(x)>f(
)
(f(x)>f(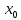 )
при x<
)
при x<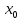
Теорема
33.Пусть
функция y=f(x)
дифференцируема в точке x=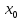 и f’(
и f’(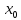 )>0(f’(x)<0)тогда
функция f(x)
возрастает (убывает) в
)>0(f’(x)<0)тогда
функция f(x)
возрастает (убывает) в
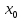
Док-во:
проведем для случая f’(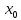 )>0
)>0
По
определению наличия производной функции
f(x)
означает, что следующий предел:
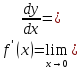
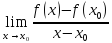 тогда в соответствии со вторым
определением функции, для любого έ>0
найдется δ>0 такое, что при Іx-
тогда в соответствии со вторым
определением функции, для любого έ>0
найдется δ>0 такое, что при Іx-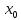 І<
δ выполняется:
І<
δ выполняется:
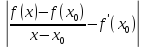 <
έ; f’(
<
έ; f’( έ<
έ<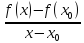 <f’(
<f’(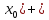 έ.выберем έ<f’(
έ.выберем έ<f’(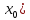 f’(
f’(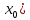 -
έ>0
,тогда
-
έ>0
,тогда
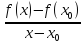 >f’(
>f’(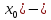 έ>0.
έ>0.
А)f(x)-f(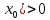 при
x>
при
x> Б)f(x)-f(
Б)f(x)-f( <0
при x<
<0
при x<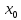
Локальный максимум и минимум функции.
Определение:
функция y=f(x)
имеет в точке
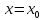 локальный макс(мин),если найдется
окрестность точки
локальный макс(мин),если найдется
окрестность точки
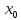 ,в
пределах которой значение f(
,в
пределах которой значение f(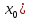 является
наибольшим(наименьшим) среди всех
значений функции в этой окрестности.
вместе локальный максимум и минимум
получили название локального экстремума.
является
наибольшим(наименьшим) среди всех
значений функции в этой окрестности.
вместе локальный максимум и минимум
получили название локального экстремума.
Теорема 34.
Пусть
функция y=f(x)имеет
локальный экстремум в точке
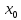 и
дифференцируема в этой точке. Тогда
f’(
и
дифференцируема в этой точке. Тогда
f’(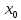 )=0.
)=0.
Док-во:
так как точка локального экстремума не
является ни точкой возрастания ни точкой
убывания функции, значит не выполняется
равенство f’(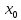 )>0,f’(
)>0,f’(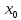 )<0,то
очевидно, что f’(
)<0,то
очевидно, что f’(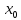 )=0.
)=0.
Теорема 35(Ролля).
Пусть
функция y=f(x)
непрерывна на сегменте
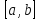 и дифференцируема в любой внутренней
точке этого сегмента. Пусть кроме того
f(a)=f(b).Тогда
внутри
и дифференцируема в любой внутренней
точке этого сегмента. Пусть кроме того
f(a)=f(b).Тогда
внутри
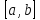 найдется точка d
, такая, что f’(d)=0.
найдется точка d
, такая, что f’(d)=0.
Док-во:
так как функция непрерывна на сегменте
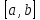 ,то
она достигает на этом сегменте своих
наибольшего M
и наименьшего m
значения. Могут реализоваться 2 случая:
,то
она достигает на этом сегменте своих
наибольшего M
и наименьшего m
значения. Могут реализоваться 2 случая:
a)значения m и M достигается на краях сегмента. Тогда из условия f(a)=f(b)следует, что M=m,но такое возможно только при f(x)=const.значит найдется точка d такая,что f’(d)=0.
Б)одно из значений m или M достигается на краю отрезка а другое внутри него в некоторой точке d,значит d-точка экстремума и f’(d)=0.
Теорема 36(Логранжа).
Пусть
функция f(x)
непрерывна на
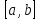 и дифференцируема в любой точке внутри
сегмента:f(b)-f(a)=f’(d)(b-a)-формула
Логранжа. d-
точка внутри
и дифференцируема в любой точке внутри
сегмента:f(b)-f(a)=f’(d)(b-a)-формула
Логранжа. d-
точка внутри
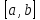 .
.
Док-во:
Построим вспомогательную функцию
F(x)=f(x)-f(a)-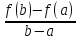 (b-a).Эта
функция удовлетворяет условиям теоремы
Ролля. Действительно, функция непрерывна
на
(b-a).Эта
функция удовлетворяет условиям теоремы
Ролля. Действительно, функция непрерывна
на
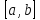 .F(a)=
.F(a)=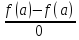 -
-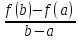 (a-a)=0;F(b)=f(b)-f(a)-
(a-a)=0;F(b)=f(b)-f(a)-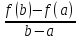 (b-a)=0
таким образом F(a)=F(b)
Вычислим F'(x):по
теореме Ролля найдется точка d
такая, что F’(d)=0=f’(d)=
(b-a)=0
таким образом F(a)=F(b)
Вычислим F'(x):по
теореме Ролля найдется точка d
такая, что F’(d)=0=f’(d)=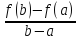 f(b)-f(a)=(b-a)f’(d).
f(b)-f(a)=(b-a)f’(d).
Теорема 37 о возрастании(убывании) функции.
Для того, чтобы f(x) возрастала(убывала) на (a,b) необходимо и достаточно, чтобы на (a,b) выполнилось f’(x)>0(<0).
Док-во:
Считается, что f(x)↑(↓)
на (a,b)
то есть функция f(x)
↑(↓) в каждой точке этого интервала,
но тогда в соответствии с теоремой 33,
для каждой точке x
из (a,b)
выполняется f’(x)>0(<0)значит
это условие выполняется на всем интервале
(a,b).
Достаточноcть
: считается, что на (a,b)
выполняется f’(x)>0(<0)Надо
доказать, что f(x)
возрастает(убывает) на (a,b).Выберем
2 произвольные точки на сегменте (a,b)
и (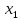 <
<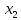 ).Тогда
на сегменте
).Тогда
на сегменте
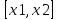 выполняется условие теоремы Логранжа.
f(x2)-f(x1)=f’(d)(x2-x1)>0.для
f’(d)>0f(x2)>f(x1)
при x2>0(<
0для f’(d)<0)(f(x2)<f(x1)при
x2>x1).
выполняется условие теоремы Логранжа.
f(x2)-f(x1)=f’(d)(x2-x1)>0.для
f’(d)>0f(x2)>f(x1)
при x2>0(<
0для f’(d)<0)(f(x2)<f(x1)при
x2>x1).
Теорема
38.
Пусть точка
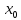 -
точка возможного экстремума функции
f(x).
И пусть f(x)
дифференцируема в некоторой окрестности
точки
-
точка возможного экстремума функции
f(x).
И пусть f(x)
дифференцируема в некоторой окрестности
точки
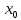 .Тогда,
если f’(x)>0(<0)в
пределах этого интервала слева от точки
.Тогда,
если f’(x)>0(<0)в
пределах этого интервала слева от точки
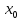 и f’(x)<0(>0)
справа от
и f’(x)<0(>0)
справа от
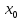 ,то
функция имеет в точке
,то
функция имеет в точке
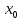 локальный максимум(минимум).
локальный максимум(минимум).
Док-во:
Проведем его для случая локального
максимума. Выберем две точки из окрестности
точки
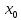 :
: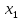 <
<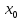 ,
,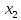 >
>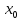 тогда
на сегментах
тогда
на сегментах
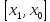 и
и
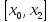 применима формула Логранжа.f(x0)-f(x1)=f’(d)(x0-x1)>0
при d
принадлежащем
применима формула Логранжа.f(x0)-f(x1)=f’(d)(x0-x1)>0
при d
принадлежащем
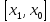 f(x0)>f(x1).
f(x0)>f(x1).
F(x2)-f(x0)=f’(d)(x2-x0)<0
при d
принадлежащем
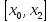
f(x0)>f(x2)
f(x0)>f(x2)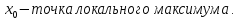
Теорема
39. Пусть
функция f(x)
дифференцируема в некоторой окрестности
точки
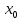 ,за исключением самой
,за исключением самой
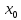 .
И пусть f(x)
непрерывна в
.
И пусть f(x)
непрерывна в
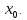 Тогда, если в пределах указанной
окрестности f’(x)>0(<0)
слева от
Тогда, если в пределах указанной
окрестности f’(x)>0(<0)
слева от
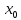 и f’(x)<0(>0)
справа от точки
и f’(x)<0(>0)
справа от точки
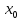 ,то
функция f(x)
имеет в точке
,то
функция f(x)
имеет в точке
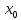 локальный
максимум(минимум).Если знак производной
функции справа и слева одинаковый, то
в
локальный
максимум(минимум).Если знак производной
функции справа и слева одинаковый, то
в
 нет
экстремума.
нет
экстремума.
Доказательство аналогично 38 теореме.
Теорема
40. Пусть
точка
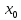 -точка
возможного экстремума функции f(x).
И пусть функция f(x)
имеет в точке
-точка
возможного экстремума функции f(x).
И пусть функция f(x)
имеет в точке
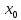 конечную вторую производную. Тогда,
если f’’(
конечную вторую производную. Тогда,
если f’’(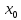 )<0,то
в
)<0,то
в
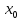 достигается локальный максимум, если
же f’’(x)>0,
то в
достигается локальный максимум, если
же f’’(x)>0,
то в
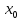 локальный минимум.
локальный минимум.
Док-во:
обозначим f’(x)
=g(x).
Тогда
f’’(x)=g’(x)
для максимума условие: f’’(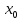 )=g’(
)=g’( )<0.
Далее в
)<0.
Далее в
Теорема 41Пусть функция x0 y=f(x) дважды дифференцируема на (a,b) Тогда, если f``(x)<0 (f``(x)>0 ) на (a,b) то график f(x) на (a,b) имеет выпуклость, направленная вверх (вниз)
Точки перегиба графика функции. Определение
Точка М(x0,y0) называется точкой перегиба графика функции y=f(x) если направление выпуклости слева и справа от т. x0 различ x0
Теорема 42
Пусть функция y=f(x) дважды дифференцируема в т. x0 и пусть т. М (x0,y0) является точной точкой перегиба графика функции. Тогда y``(x0)=0
Первое и второе достаточное условие перегиба
Теорема 43
(1 условие) пусть функция y=f(x) дважды дифференцируема в некоторой окрестности т. x0 и пусть f``(x0)=0, тогда есди вторая производная функции f(x) слева и справа от точки x0 в пределах выбранной окрестности имеет различный знак, то график функции в т. М (x0,y0) имеет перегиб.
Теорема 44
Пусть функция y=f(x) – трижды дифференцируема в т. x0 , и пусть выполняется f``(x0)=0, f``(x0)≠0. Тогда график функции f(x) в т. М (x0,y0) имеет перегиб.
Третье достаточное условие экстремума и перегиба
Теорема 45
Пусть функция y=f(x) – n-раз дифференцируема в окрестности т. x0 и (n+1) раз дифференцируема в самой т. x0 .Пусть кроме того выполняется
f``(x0)= f```(x0)=… f(n)(x0)=0, f(n+1)(x0)≠0 , тогда 1) если число n-четное, то график функции f(x) в т. М (x0,y0) имеет перегиб.2) если n-нечетное число и кроме того f`(x0)=0, f(n+1)(x0)<0 (f(n+1)(x0)>0) , то фунуция f(x) в т. x0 имеет локальный максимум ( ЛОКАЛЬНЫЙ МИНИМУМ)
Критерий Коши о существовании предела функции(условие Коши, теорема 47)
Определение: считает значений аргумента, что ф-ция y=f(x) удовлетворяет условию Коши в точке x=x0 если для любого ε>0 найдется число δ>0, такое, что для любой пары x`, x`` значений аргумента, удовлетворяющих неравенства
0<|x0-x`|< δ 0<|x0-x``|<δ выполняется неравенство | f(x`)- f(x``)|<ε
Теорема 47(критерий коши) для того чтобы функция y=f(x) имела в т. x0 конечное предельное значение, необходимо и достаточно, чтобы она удовлетворяла в т. x0 условие Коши (без доказательства)
Ограниченность функции непрерывной на сегменте. Определение
Функция y=f(x) называется ограниченной сверху(снизу) на множ. {x} , если найдется число M(m) такое, что для всех x€{x} выполняется неравн. F(x)≤M(f(x)≥m)
Определение: Функция y=f(x) называется ограниченной на множистве {x} с обеих сторон, если она ограничена на этом множестве и снизу и сверху,т.е. m≤f(x)≤M (при x€{x})
Теорема 48(первая теорема Вейерштрасса)
Пусть ф -ция y=f(x) непрерывна на сегменте [a,b]. Тогда она ограничена на этом сегменте.Док-во: рассмотрим ограниченность сверху. Предположим противоположное , т.е. будем считать, что функция неограниченна сверх, тогда для любого сколь угодно большого числа A=n (нат.ур) найдетсе хотя бы одно значение x€[a,b] такое, что выполняется f(xn)>n . Отсюда следует, что последовательность {f(xn)}, соответствующая последовательности аргументов {xn} (xn€[a,b]) является бесконечно большой.
Последовательность аргумента {xn} является ограниченной, т.к. все элементы xn€[a,b]. Тогда по теореме Больцано-Вейерштрасса из {xn} можно выбрать последовательность {xkn}, сходящаяся к некотор. Числу ξ€[a,b]
Отсюда следует, что в силу непрерывности ф-ции f(x) на [a,b] подпоследовательность {f(xn)} должна быть бесконечно большой, как последовательности {f(xn)} → первоначальное предположение о неограниченности сверху ф-ции f(x) а [a,b] неверно.
Точная верхняя и нижняя грани функции на сегменте(определение)
Число M(m) называется точной верхнейь (нижней) гранью функции f(x) на множестве {x} , если: 1) для всех x€{x} выполняется неравенство f(x)≤M(f(x)≥m). 2) для любого ε>0 найдется хотя бы одно значение аргумента x`€{x} такое что f(x`)>M-ε(f(x`)<m+ε)
Теорема 49(2-я теорема Вейерштрасса)
Пусть
ф -ция y=f(x)
непрерывна на сегменте [a,b].
Тогда она достигает своих точных верхней
и нижней граней на [a,b].
Док-во:
проведем
для верхней грани. Пусть М-точная верхняя
грань f(x)
на [a,b]
. предположим, что М не достигается на
[a,b],
тогда справедливо неравенство f(x)<M
M-f(x)>0
для всех xε[a,b].
Введем дополнительную функцию F(x)=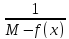 ;
т.к. функция f(x)
непрерывна на [a,b],
то в соответствии с первой теоремой
Вейерштрасса F(x)
ограничена на [a,b]
;
т.к. функция f(x)
непрерывна на [a,b],
то в соответствии с первой теоремой
Вейерштрасса F(x)
ограничена на [a,b]
F(x)=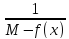 ≤B→M-f(x)
≥
≤B→M-f(x)
≥ → M-
→ M-
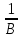 ≥f(x)
→ f(x)≤M-
≥f(x)
→ f(x)≤M-
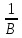 =M`
для
всех x€[a,b].
=M`
для
всех x€[a,b].
M`- верхняя грань (M`<M). Но это противоречит тому, что M является точной верхней гранью. Следовательно, первоночальное предположение о том, что точная верхняя грань не достигается на [a,b] неверно.
Теорема
50 (теорема Коши):
пусть функции f(x)
и g(x)
непрерывны на [a,b]
и дифференцируемы в каждой внутренней
точке сегмента [a,b].
Пусть кроме того, g`(x)≠
во всех внутренних точках [a,b]
найдется т. Ξ такая, что выполняется
равенство
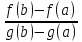 =
=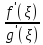 – формула Коши
– формула Коши
Док-во:
составим вспомогательную функцию
F(x)=f(x)-f(a)
-
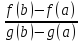 *
[g(x)-g(a)]
. функция f(x)
непрерывна на [a,b]
, далее F(a)=F(b)=0.
Тогда функция f(x)
удовлетворяет условию теоремы Коши. В
соответствии с этой теоремой внутри
сегмента [a,b]
найдется т. ξ такая , что F`(ξ)=0
*
[g(x)-g(a)]
. функция f(x)
непрерывна на [a,b]
, далее F(a)=F(b)=0.
Тогда функция f(x)
удовлетворяет условию теоремы Коши. В
соответствии с этой теоремой внутри
сегмента [a,b]
найдется т. ξ такая , что F`(ξ)=0
F`(ξ)=f`(ξ)- *g`(
*g`(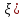 =0
→ f`(ξ)=
=0
→ f`(ξ)=
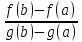 *
g`(
*
g`(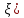 .
.
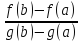 =
=