
matan_vse_k_ekzamenu_za_1_semestr
.docx
Теорема
14 (О двух милиционерах):
Пусть
 и
и
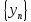 сходящиеся последовательности и сходятся
к одному и тому же пределу a.
Пусть кроме того последовательность
сходящиеся последовательности и сходятся
к одному и тому же пределу a.
Пусть кроме того последовательность
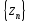 начиная с некоторого номера N*
удовлетворяет неравенствам
начиная с некоторого номера N*
удовлетворяет неравенствам
 .
Тогда Последовательность
.
Тогда Последовательность
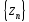 сходится и её пределом является число
a.
Доказательство:
Из исходных неравенств
сходится и её пределом является число
a.
Доказательство:
Из исходных неравенств
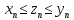 составим следующие неравенства
составим следующие неравенства
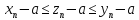 .
Тогда при n
≥ N*
выполняется
.
Тогда при n
≥ N*
выполняется
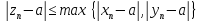 .
Выберем произвольное
.
Выберем произвольное
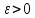 ,
тогда в силу сходимости последовательностей
,
тогда в силу сходимости последовательностей
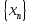 и
и
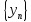 должны выполняться неравенства
должны выполняться неравенства
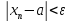 при n
≥
при n
≥
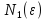 и
и
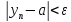 при n
≥
при n
≥
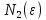 .
Тогда при n
≥ N
= max{N*,
.
Тогда при n
≥ N
= max{N*,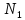 ,
,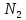 }
выполняется сразу три неравенства
}
выполняется сразу три неравенства
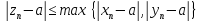 ;
;
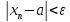 ;
;
 =>
=>
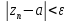 ,
т.е. последовательность
,
т.е. последовательность
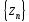 сходится и её пределом является число
a,
ч.т.д.
сходится и её пределом является число
a,
ч.т.д.
Монотонные
последовательности (определение,
примеры). Определение:
последовательность
{Xn}
называется неубывающей (невозрастающей),
если для любого номера, начиная с номера
2, каждый последующий элемент {Xn}
не меньше (не больше) предыдущего, т.е.
элементы последовательности подчиняются
неравенствам:
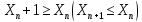 .Вместе
неубывающие и невозрастающие
последовательности называются
монотонными. Примеры:
1)Последовательность
1,1,
.Вместе
неубывающие и невозрастающие
последовательности называются
монотонными. Примеры:
1)Последовательность
1,1,
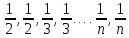 - есть невозрастающая последовательность.
2)Последовательность 1,1,2,2….n,n
– есть неубывающая последовательность.
Если
- есть невозрастающая последовательность.
2)Последовательность 1,1,2,2….n,n
– есть неубывающая последовательность.
Если
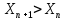 , то последовательность называется
возрастающей. Если
, то последовательность называется
возрастающей. Если
 , то последовательность называется
убывающей. Обе эти последовательности
являются строго монотонными.
, то последовательность называется
убывающей. Обе эти последовательности
являются строго монотонными.
Ограниченные
множества, точная верхняя и нижняя грани
множества (1-ое и 2-ое определения).
Определение:
Число М
называется верхней (нижней) гранью
множества {X},
если каждый элемент этого множества
удовлетворяет неравенству X .
Определение:
Наименьшая из верхних граней множества
{x}
называется точной верхней гранью,
обозначается:
.
Определение:
Наименьшая из верхних граней множества
{x}
называется точной верхней гранью,
обозначается:
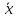 =sup{x}
— супремум.
=sup{x}
— супремум.
Теорема
15:
Если неубывающая (невозрастающая)
последовательность ограниченна сверху
(снизу), то она сходится. Доказательство:
Пусть
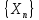 является
неубывающая последовательность, тогда
для любого
является
неубывающая последовательность, тогда
для любого
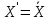 –
ε
найдётся число
–
ε
найдётся число
 такое ,что выполняется неравенство:
такое ,что выполняется неравенство:
 – ε;
– ε;
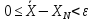 ;
Выберем номера n
;
Выберем номера n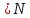 ;
;
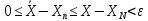 ;
;
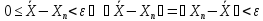 при n<N.
Последовательность
при n<N.
Последовательность
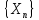 является сходящейся. Теорема доказана.
является сходящейся. Теорема доказана.
Сходимость
последовательности
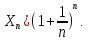 Исследуем
сходимость последовательности {
Исследуем
сходимость последовательности { },
элемент
},
элемент
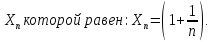 Покажем,
что эта последовательность
Покажем,
что эта последовательность
 Для
доказательства возрастания
последовательности надо сравнить
Для
доказательства возрастания
последовательности надо сравнить
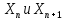 .
Распишем выражение для
.
Распишем выражение для
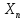 , используя формулу Бинома- Ньютона:
, используя формулу Бинома- Ньютона: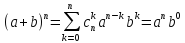 +
+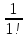
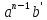 +
+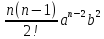 +
+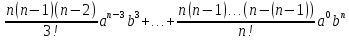 ;
;
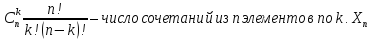 =
= =
1+
=
1+ )
+
)
+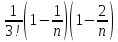 +…+
+…+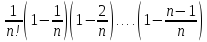 ;
Xn+1
=2+
;
Xn+1
=2+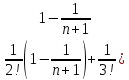 )(1
)(1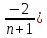 +…+
+…+ ;
1
;
1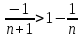 ;
;
 последовательность {
последовательность { }
возрастающая. Покажем, что {
}
возрастающая. Покажем, что {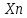 }
является ограниченной сверху
последовательностью.
}
является ограниченной сверху
последовательностью.
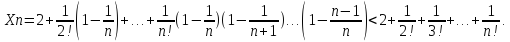 Используем
следующее неравенства:
Используем
следующее неравенства:
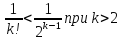 ;
Xn<2+
;
Xn<2+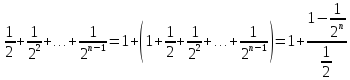 =1+
=1+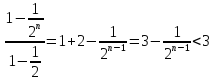 .
Таким образом последовательность {Xn}
является возрастающей и ограниченной
сверху. Следовательно по теореме (15)
она является сходящейся.
.
Таким образом последовательность {Xn}
является возрастающей и ограниченной
сверху. Следовательно по теореме (15)
она является сходящейся.

Предельное
значение функции, левое и правое
предельные значения (определения).
Рассмотрим
функцию y=f(x),
заданную на множестве {X}.
Определение:
Число b
называется предельным значением функции
y=f(x)
в точке X=X0
,если для любой сходящейся к X0
последовательности {Xn}
значений аргумента, соответствующая
последовательность {f(Xn)}
значений функции сходится к b.
Символическая
запись:
 Определение:
Число b
называется предельным значением функции
y=f(x)
справа (слева) в точке X=X0,
если для любой сходящейся к X0
последовательности {Xn}
значений аргумента , элементы которой
больше (меньше) X0,
соответствующая последовательность
{f(Xn)}
значений функции сходится к b.
Определение:
Число b
называется предельным значением функции
y=f(x)
справа (слева) в точке X=X0,
если для любой сходящейся к X0
последовательности {Xn}
значений аргумента , элементы которой
больше (меньше) X0,
соответствующая последовательность
{f(Xn)}
значений функции сходится к b.
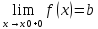 ;
;
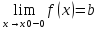 .
.
Теорема
16.
Пусть
функция f(x)
и g(x)
определённая на одном и том же множестве
{X},
имеют точки X=X0
предельное значение соответственно в
токах b
и c.
Тогда функции f(x) имеют
в точке X0
предельное
значение соответственно b
имеют
в точке X0
предельное
значение соответственно b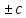 ,b*c,
,b*c,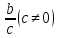 .
Доказательство:
Выберем произвольную последовательность
аргументов {X}
сходящуюся к X0.
Тогда соответствующие последовательности
{f(Xn)}
и {g(Xn)}
сходятся к b
и c
по свойствам сходящихся последовательностей
последовательности {f(Xn)
.
Доказательство:
Выберем произвольную последовательность
аргументов {X}
сходящуюся к X0.
Тогда соответствующие последовательности
{f(Xn)}
и {g(Xn)}
сходятся к b
и c
по свойствам сходящихся последовательностей
последовательности {f(Xn)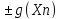 },
{f(Xn)*g(Xn)},
{
},
{f(Xn)*g(Xn)},
{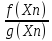 }
являются сходящимися к пределам
соответственно: (b
}
являются сходящимися к пределам
соответственно: (b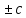 ),b*c,
),b*c,
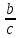 .
Теорема доказана.
.
Теорема доказана.
Бескрнечно
малые и бесконечно большие функции
(определение). Часто
сравнивают бесконечно малые функции
со стандартными, например, с функцией
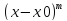 .
Тогда, если
.
Тогда, если
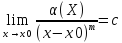 , то считается что бесконечно малая
функция
, то считается что бесконечно малая
функция
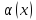 имеет в точке x0
m-тый
порядок малости. Функция f(x)
называется бесконечно большой в точке
x=x0
справа (слева), если для любой сходящейся
к X0
последовательности {Xn},
все элементы которой больше (меньше)
X0,
соответствующая последовательность
{f(Xn)}
значение функции является бесконечно
большой последовательностью определённого
знака. Символическая
запись:
имеет в точке x0
m-тый
порядок малости. Функция f(x)
называется бесконечно большой в точке
x=x0
справа (слева), если для любой сходящейся
к X0
последовательности {Xn},
все элементы которой больше (меньше)
X0,
соответствующая последовательность
{f(Xn)}
значение функции является бесконечно
большой последовательностью определённого
знака. Символическая
запись:
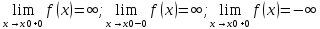
Сравнение
бесконечно малых и бесконечно больших
функций. Правило
сравнения бесконечно больших функций
сходны с правилом сравнения бесконечно
малых функций. Пусть функции A(x)
u
B(x)
являются бесконечно большими
(положительного знака) в точке X0
справа, тогда: 1)Функция A(x)
считается бесконечно большой в точке
X0
справа большего порядка роста, чем B(x),
если выполняется:
 ;
2)Функция A(x)
считается бесконечно большой в точке
X0
справа одинакового порядка роста с
B(x),если
выполняется:
;
2)Функция A(x)
считается бесконечно большой в точке
X0
справа одинакового порядка роста с
B(x),если
выполняется:
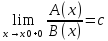 (c
- константа) Пример:
Сравнить бесконечно большие в точке
X0=0
справа функции: A(x)
(c
- константа) Пример:
Сравнить бесконечно большие в точке
X0=0
справа функции: A(x)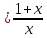 ;
B(x)=
;
B(x)=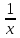 ;
;
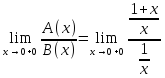 =1 A(x),
B(x)
– одинакового порядка роста.
=1 A(x),
B(x)
– одинакового порядка роста.
Лемма
2:
Пусть
в некоторой
 -
окрестности точки X0
заданы функции f(x),g(x),h(x).
Пусть кроме того функции f(x)
и g(x)
имеют в точке X0
одинаковое предельное значение, равное
b,
тогда если в указанной окрестности
выполняется неравенство: f(x)
-
окрестности точки X0
заданы функции f(x),g(x),h(x).
Пусть кроме того функции f(x)
и g(x)
имеют в точке X0
одинаковое предельное значение, равное
b,
тогда если в указанной окрестности
выполняется неравенство: f(x)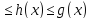 ,
то предельное значение функции h(x)
существует и равно b.
Доказательство:
Выберем из
,
то предельное значение функции h(x)
существует и равно b.
Доказательство:
Выберем из
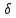 -
окрестности точки x0
произвольную последовательность {Xn}
сходящуюся к X0.
Тогда по определению последовательности
{f(Xn)},{g(Xn)}
являются сходящимися к числу b.
Кроме этого для элементов последовательностей
{f(Xn)},{g(Xn)},{h(Xn)},
выполняются неравенства:
-
окрестности точки x0
произвольную последовательность {Xn}
сходящуюся к X0.
Тогда по определению последовательности
{f(Xn)},{g(Xn)}
являются сходящимися к числу b.
Кроме этого для элементов последовательностей
{f(Xn)},{g(Xn)},{h(Xn)},
выполняются неравенства:
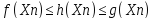 тогда в соответствии с теоремой (14) (о
двух миллиционерах)последовательность
{h(Xn)}
является к тому же числу b.
Лемма доказана.
тогда в соответствии с теоремой (14) (о
двух миллиционерах)последовательность
{h(Xn)}
является к тому же числу b.
Лемма доказана.
Теорема
17(Первый замечательный предел):
Предельное
значение функции
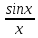 в точке x=0
существует и равно единице, т.е.
в точке x=0
существует и равно единице, т.е.
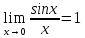 .
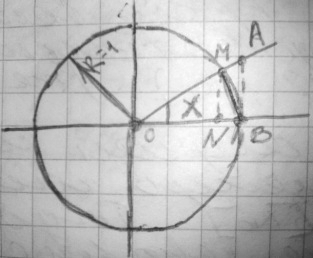
Доказательство:
Используем следующее построение:
.
Доказательство:
Используем следующее построение:
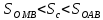 ; 0<x<
; 0<x<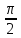 ;
см. рисунок в лекции (круг):
;
см. рисунок в лекции (круг):
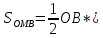 MN
=
MN
=
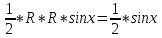 ;
;
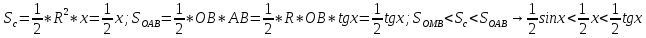 ,
0<sinx<x<tgx
, x<tgx=
,
0<sinx<x<tgx
, x<tgx=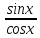 , sinx<x
,
, sinx<x
,
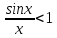 ,
,
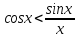 ,
,
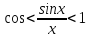 .
Тогда в соответствии с Леммой (2) предельное
значение функции
.
Тогда в соответствии с Леммой (2) предельное
значение функции
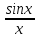 существует и равно 1.
существует и равно 1.
Теорема
18.(Второй замечательный предел):
Предельное
значение функции
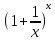 при x
при x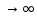 существует и равно e,
т.е.
существует и равно e,
т.е.
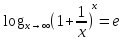 .
Доказательство:
Выберем произвольную бесконечно большую
последовательность {Xn}.
Случай, когда
.
Доказательство:
Выберем произвольную бесконечно большую
последовательность {Xn}.
Случай, когда
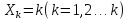 мы уже рассматривали. Рассмотрим теперь
случай, когда
мы уже рассматривали. Рассмотрим теперь
случай, когда
 не целое. Обозначим целую часть
не целое. Обозначим целую часть
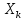 через
через
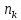 , т.е.
, т.е.
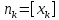 , тогда выполняются очевидные неравенства:
, тогда выполняются очевидные неравенства:
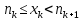 ;
;
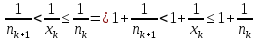 ;
;
 ;
;
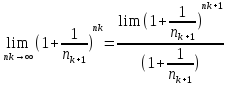 =e;
=e;
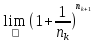 =
=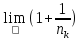 = e.Тогда
в соответствии с теоремой(14)
последовательность {
= e.Тогда
в соответствии с теоремой(14)
последовательность {
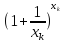 }
является сходящейся (при
}
является сходящейся (при
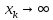 ).
Замечание
1:
Предельное значение функции
).
Замечание
1:
Предельное значение функции
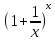 , при x
, при x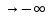 также равно e
(x=
также равно e
(x= ).
Замечание
2:
Справедлива и следующая запись второго
замечательного предела:
).
Замечание
2:
Справедлива и следующая запись второго
замечательного предела:
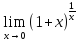 = e.
= e.
Предельные
значения некоторых функций.
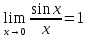 ;
;
 ;
;
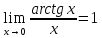 ;
;
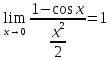 ;
;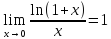 ;
;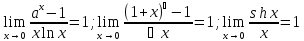 ;
;
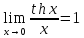
Формулы
эквивалентов.
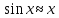 ;
tg
x
;
tg
x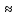 x;
arcsin
x
x;
arcsin
x x;
arctg
x
x;
arctg
x x;
cos
x
x;
cos
x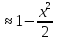 ;
ln(1+x)
;
ln(1+x)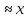 ;
;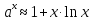 ;
;
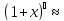 1+
1+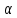 x;
sh
x;
sh
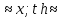 x.
x.
Предельные
значения выражений вида
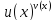 .
Воспользуемся
представлением
.
Воспользуемся
представлением
 через экспоненту
через экспоненту
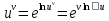 .
С помощью этого выражения можно раскрыть
неопределенности
.
С помощью этого выражения можно раскрыть
неопределенности
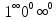 .
Рассмотрим выражение
.
Рассмотрим выражение
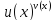 при
при
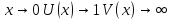 .
.
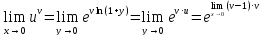 .
Неопределенности вида
.
Неопределенности вида
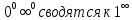 ,
если сделать замену. U=
,
если сделать замену. U=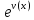 V=ln(u(x)).
V=ln(u(x)).
Непрерывность
функции, непрерывность справа и слева
(определения). Определение:
Функция y=f(x)
называется
непрерывной в точке x=
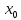 ,
если предельное значение этой функции
в точке
,
если предельное значение этой функции
в точке
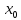 существует и равно частному значению
функции в точке
существует и равно частному значению
функции в точке
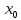 .
Определение:
Функция
y=f(x)
называется
непрерывной справа (слева) в точке x=
.
Определение:
Функция
y=f(x)
называется
непрерывной справа (слева) в точке x=
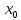 ,
если предельное значение этой функции
справа (слева) в точке
,
если предельное значение этой функции
справа (слева) в точке
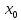 существует и равно частному значению
функции в точке
существует и равно частному значению
функции в точке
 .
.
Точки
разрыва функции (определение, классификация,
примеры). Определение:
В точке, в которой не выполняется
свойство непрерывности, называется
точками разрыва функции. (Например,
функция y=sgn(x)
имеет разрыв в точке x=0).
Классификация
точек разрыва:
рассмотрим вначале внутренние точки
разрыва функции. 1
тип - Устранимый разрыв:
Точка
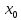 называется точкой разрыва функции
y=f(x),
если
в этой точке существует конечное
предельное значение функции f(x),
но
функция в этой точке либо неопределена,
либо ее частное значение f(
называется точкой разрыва функции
y=f(x),
если
в этой точке существует конечное
предельное значение функции f(x),
но
функция в этой точке либо неопределена,
либо ее частное значение f(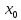 )
не
совпадает с предельным значением f(x)
в
точке
)
не
совпадает с предельным значением f(x)
в
точке
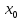 (
(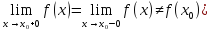 .
(Например, f(x)=
.
(Например, f(x)=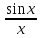 в точке
в точке
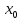 =0).
2
тип – Разрыв первого рода (скачок): Точка
=0).
2
тип – Разрыв первого рода (скачок): Точка
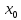 называется точкой разрыва первого рода
функции y=f(x),
если функция f(x)
имеет в точке
называется точкой разрыва первого рода
функции y=f(x),
если функция f(x)
имеет в точке
 конечное, но не равное друг другу левое
и правое предельное значение (
конечное, но не равное друг другу левое
и правое предельное значение (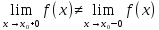 ).
(Например, f(x)=sgn(x)
в точке
).
(Например, f(x)=sgn(x)
в точке
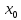 =0,
=0,
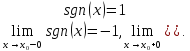 3
тип – Разрыв второго рода:
Точка
3
тип – Разрыв второго рода:
Точка
 чкой
разрыва второго рода функции y=f(x),
если
хотя бы одно одностороннее предельное
значение функции в
чкой
разрыва второго рода функции y=f(x),
если
хотя бы одно одностороннее предельное
значение функции в
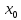 равно
равно
 или
не существует. (Например, f(x)=tg
x
в точке x=
или
не существует. (Например, f(x)=tg
x
в точке x=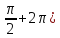 .
Для граничных точек области определения
имеют смысл точки разрыва второго рода
и устранимого разрыва.
.
Для граничных точек области определения
имеют смысл точки разрыва второго рода
и устранимого разрыва.
Теорема
19:
Пусть фунции f(x)
и g(x)
заданы на одном и том же множестве и
непрерывны в точке x=
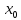 .
Тогда функции f(x)
.
Тогда функции f(x)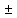 g(x),
f(x)
g(x),
f(x) g(x),
f(x)/g(x)
(при g(x)
g(x),
f(x)/g(x)
(при g(x)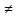 0)
также непрерывна в точке x=
0)
также непрерывна в точке x=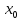 .
Доказательства:
По определению непрерывности функции
f(x)
и g(x)
имеют предельное значение в точке
.
Доказательства:
По определению непрерывности функции
f(x)
и g(x)
имеют предельное значение в точке
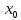 .
Тогда по теореме 16 (о функциях, имеющих
предельное значение) и функции f(x)
.
Тогда по теореме 16 (о функциях, имеющих
предельное значение) и функции f(x)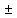 g(x),
f(x)
g(x),
f(x) g(x),
f(x)/g(x)
также
имеют предельное значение в точке
g(x),
f(x)/g(x)
также
имеют предельное значение в точке
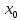 .
При этом выполняется
.
При этом выполняется
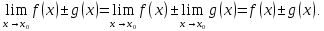 Ч.т.д.
Ч.т.д.
Определение
предельного значения и непрерывности
на языке
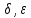 .
Определение:
Число
b
называется предельным значением функции
f(
.
Определение:
Число
b
называется предельным значением функции
f(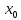 ),
если
для любого
),
если
для любого
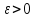 найдется
число
найдется
число
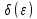 такое,
что для всех x,
удовлетворяющих неравенству
такое,
что для всех x,
удовлетворяющих неравенству
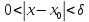 ,
выполняется неравенство
,
выполняется неравенство
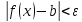 .
Определение:
Функция
f(x)
называется непрерывной в точке
.
Определение:
Функция
f(x)
называется непрерывной в точке
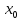 ,
если для любого
,
если для любого
 найдется число
найдется число
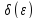 такое,
что для всех x,
удовлетворяющих неравенству
такое,
что для всех x,
удовлетворяющих неравенству
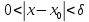 ,
выполняется неравенство
,
выполняется неравенство
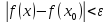 .
.
Сложная
функция и ее непрерывность
(определение)Определение:
Пусть функция x=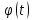 задана на множестве
задана на множестве
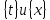 представляет собой множество значений
этой функции. Пусть кроме того на
множестве
представляет собой множество значений
этой функции. Пусть кроме того на
множестве
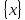 задана функция y=f(x).
Тогда считается, что на множестве {t}
задана сложная функция y=f(
задана функция y=f(x).
Тогда считается, что на множестве {t}
задана сложная функция y=f(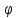 (t))=F(t)
аргумента
t.
(t))=F(t)
аргумента
t.
Теорема
20:
Пусть функция x=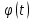 ,
заданная
на множестве
,
заданная
на множестве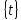 и имеющая область значений
и имеющая область значений
 ,
непрерывна в точке
,
непрерывна в точке
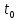 .
Пусть кроме того функция y=f(x),
заданная на множестве
.
Пусть кроме того функция y=f(x),
заданная на множестве
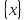 непрерывна в точке
непрерывна в точке
 =
=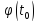 .
Тогда
сложная функция непрерывна в точке
.
Тогда
сложная функция непрерывна в точке
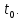 Доказательства:
Выберем произвольную последовательность
Доказательства:
Выберем произвольную последовательность
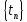 для n,
сходящихся к точке
для n,
сходящихся к точке
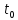 .
Тогда, в соответствии с определением,
последовательность функции
.
Тогда, в соответствии с определением,
последовательность функции
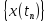 сходится к
сходится к
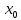 =
=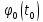 .
В
свою очередь в силу непрерывности
функции y=f(x)
в точке
.
В
свою очередь в силу непрерывности
функции y=f(x)
в точке
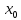 последовательность функций
последовательность функций
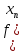 должна сходиться к f(
должна сходиться к f(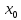 ),
то есть
),
то есть
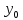 =
f(
=
f(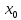 )
= f(
)
= f(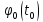 )=F(
)=F(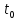 ).
Так как последовательность выбрана
произвольно, то это обозначает
непрерывность сложной функции F(x)
в
точке
).
Так как последовательность выбрана
произвольно, то это обозначает
непрерывность сложной функции F(x)
в
точке
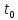 .
.
Монотонные
функции (определение, примеры). Определение:
Функция y=f(x)
называется неубывающей (невозрастающей)
на множестве
 ,
если для любой пары чисел
,
если для любой пары чисел
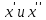 (из этого множества и удовлетворяющие
неравенству
(из этого множества и удовлетворяющие
неравенству
 )
выполняется неравенство f(
)
выполняется неравенство f(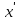 )<f(
)<f(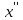 )
(f(
)
(f(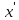 )>f(
)>f(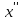 )).
Вместе неубывающие и невозрастающие
функции называются монотонными. Примеры:
y=x
возрастающая на
)).
Вместе неубывающие и невозрастающие
функции называются монотонными. Примеры:
y=x
возрастающая на
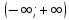 ,
y=x
sgn
(x)
убывает на
,
y=x
sgn
(x)
убывает на
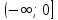 и возрастает на
и возрастает на
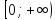 .
.
Лемма
3:
Для того, чтобы строго монотонная на
сегменте [a;b]
функция y=f(x)
была непрерывная, необходимо и достаточно,
чтобы любое число γ, заключенное между
α=f(a)
и β=f(b)
было
значением функции (без доказательств).
Следствие:
Пусть функция y=f(x)
строго
монотонна и непрерывна на сегменте[a;b]
и множество значений функции есть
сегмент [α;β]
(или [β;
α]),
где α=f(a)
и β=f(b).
Тогда на сегменте [α;β]
(или [β;
α])
определяется строго монотонная и
непрерывная обратная функция x= (y).
(y).
Обратные
функции для некоторых элементарных
функций. Показательная
функция:
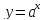 ;
;
 ;
x
;
x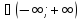 ;
y
;
y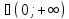 .
Синус:
y=sin
x;
рассмотрим главное значение для
.
Синус:
y=sin
x;
рассмотрим главное значение для
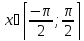 ;
x=arcsin
y;
для
x
;
x=arcsin
y;
для
x x=Arcsin
y
=
x=Arcsin
y
=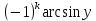 +
+ .
Косинус:
y=cos
x;
рассмотрим главное значение для
.
Косинус:
y=cos
x;
рассмотрим главное значение для
 ;
x=arccos
y;
для
x
;
x=arccos
y;
для
x x=Arccos
y
=
x=Arccos
y
=
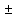 arccos
y
+2
arccos
y
+2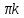 .
Тангенс:
y=tg
x;
рассмотрим главное значение для
.
Тангенс:
y=tg
x;
рассмотрим главное значение для
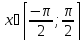 ;
x=arctg
y;
для
x
;
x=arctg
y;
для
x x=Arctg
y
=arctg
y+
x=Arctg
y
=arctg
y+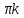 .
Котангенс: y=ctg
x;
рассмотрим главное значение для
.
Котангенс: y=ctg
x;
рассмотрим главное значение для
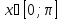 ;
x=arcctg
y;
для
x
;
x=arcctg
y;
для
x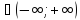 x=Arcctg
y
= arcctg
y
+2
x=Arcctg
y
= arcctg
y
+2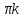 .
.
