Лекция 5. Фазовый портрет колебательной системы.

В любой колебательной системе с одной степенью свободы смещение (t) и скорость меняются со временем. Состояние системы в каждый момент времени можно характеризовать двумя значениямиии на плоскости этих переменных это состояние однозначно определяется положением изображающей точки P с координатами значениямии. С течением времени изображающая точка P будет перемещаться по кривой, которую называют фазовой траекторией движения (рис. 1.10).

Рис.5.1. Фазовый портрет

Плоскость переменных значениями и называется фазовой плоскостью. Семейство фазовых траекторий образует фазовый портрет колебательной системы. Анализ фазового портрета дает хотя и не полную, но обширную информацию о колебательной системе. К построению такого портрета прибегают тогда, когда не удается решить аналитически уравнение, описывающее сложные колебания. В первую очередь это относится к нелинейным колебаниям, анализ которых затруднен из-за отсутствия за редким исключением точных решений нелинейных уравнений.

Приведем пример построения фазовой траектории. Пусть небольшой упругий шарик брошен вертикально вверх с начальной скоростью (рис.5.2). Если пренебречь сопротивлением воздуха, то скорость шарика будет изменяться со временем по закону, гдеg− ускорение свободного падения. Изменение координаты шарика с течением времени описывается функцией . Поднявшись на максимальную высо соту, шарик начнет падать, упадет на горизонтальную поверхность и отразится от неё.

Рис. 5.2. Периодическое движение прыгающего шарика

Если удар можно считать абсолютно упругим, то скорость шарика после удара примет первоначальное значение, после чего движение шарика будет повторяться. Графики зависимостей координаты и скорости шарика от времени показаны на рис.

Рис.5.3. Фазовый портрет гармонических колебаний

Эти же функции значениями иопределяют в параметрической форме линию на фазовой плоскости – фазовую траекторию движения шарика. Эта линия показана на рис. Понятно, что при периодическом движении фазовая траектория является замкнутой, точка проходит одни те же положения через период. На фазовой траектории принято указывать направление движения: при положительной скорости координата возрастает, а при отрицательной скорости координата убывает.

Вначале рассмотрим пример простейших гармонического колебания вида . Поскольку скорость

опережает смещение по фазе на, то фазовая траектория будетэллипсом. Точка P будет двигаться по эллиптической траектории по часовой стрелке (при смещениеувеличивается, а при- смещение уменьшается (рис. 5.4)).

Рис. 5.4. Фазовый портрет

Параметры эллипса определяются энергией, запасенной гармоническим осциллятором. Потенциальная энергия пружинного маятника пропорциональна квадрату смещения:

(1.24)

Кинетическая энергия пропорциональна квадрату скорости:

(1.25)

Если принять во внимание равенство то легко видеть, что взаимопревращения одного вида энергии в другой за период происходят дважды. При этом полная энергия системы остается постоянной:

(1.26)

Равенство (1.26) как раз и является уравнением эллипса, которое можно переписать в более удобном виде:

(1.27)

Фазовый портрет гармонического осциллятора представляет собой семейство эллипсов, каждому из которых соответствует энергия запасенная осциллятором.

Положение равновесия в точке 0 на фазовой плоскости является особой точкой и называется особой точкой типа "центр".

Линейный осциллятор с затуханием. Диссипация энергии, обусловленная наличием потерь, оказывает принципиальное влияние на характер движения системы. Наиболее простые закономерности проявляются в системах с полной диссипацией энергии, когда силы трения действуют по всем степеням свободы, а поступление энергии извне отсутствует. Рассмотрим процессы в линейном диссипативном осцилляторе, когда сила трения пропорциональна скорости изменения координаты. Примером такой системы служит колебательный контур, содержащий активное сопротивление R. Уравнение контура

    (19)

заменой переменных сводится к безразмерной форме

        (20)

При d = 0 имеем консервативный линейный осциллятор, рассмотренный выше. Введение малого трения качественно меняет фазовый портрет системы. Для 0 < d < 1 решением уравнения (20) является

      (21)

где A и  — произвольные постоянные, определяемые начальными условиями. На фазовой плоскости для любых начальных данных имеют место скручивающиеся спирали, по которым фазовые точки асимптотически приближаются к началу координат, характеризуя затухающий колебательный процесс. Нуль координат является особой точкой системы, которая в случае d < 1 есть устойчивый фокус (рис. 3, а). Если коэффициент трения d > 1, процесс в системе апериодический:

    (22)

и фазовые траектории выглядят как семейство характерных кривых, по которым, как и в предыдущем случае, изображающие точки стремятся к нулю координат (рис. 5.5). Особая точка в указанных условиях является устойчивым узлом.

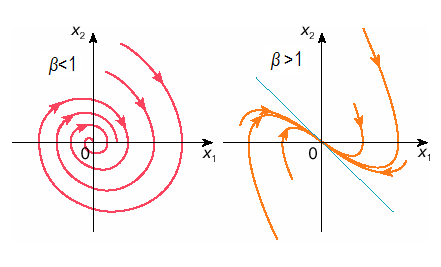
Рис.5.5. Фазовый портрет диссипативного ( с потерей энергии) осциллятора с параметрами коэффициента затухания β<1 (периодический режим) и β >1 (апериодический режим)

Итак, при любых значениях физических параметров системы, когда β>0 , диссипативный маятник характеризуется единственным глобально устойчивым состоянием равновесия в нуле фазовых координат. Независимо от выбора начальных условий наблюдается затухающее колебательное или апериодическое движение. При  любая (!) изображающая точка стремится к началу координат в устойчивый фокус либо узел.

Описанное свойство является общим для динамических систем с полной диссипацией энергии. Положения равновесия типа устойчивого фокуса или узла являются здесь глобально притягивающими в том смысле, что фазовые траектории из любой точки фазового пространства асимптотически к ним стремятся. Стационарные незатухающие колебания в линейных диссипативных системах оказываются невозможными. С физической точки зрения это понятно — нет условий поддержания колебаний. Энергия, расходуемая на преодоление сил трения, не восполняется.

Нелинейные колебания

С увеличением энергии возрастают амплитуды колебаний смещения и скорости Колебания, как правило, перестают быть гармоническими, а фазовые траектории - эллипсами.

Рис. 5.6. Колебательное или вращательное движение массы

Проанализируем на фазовой плоскости колебания математического маятника при произвольных углах отклонения от положения равновесия. При этом будем считать, что точечная масса прикреплена не к нити, а к жесткому невесомому стержню длины Первое из уравнений запишем в виде

(1.28)

Это нелинейное уравнение не имеет точного аналитического решения, поэтому позднее мы приведем его приближенное решение. Однако многие закономерности таких колебаний можно проанализировать с использованием фазового портрета на плоскости С этой целью уравнение движение надо преобразовать к такому виду, чтобы в нем остались только эти переменные, а время было бы исключено. Для этого угловое ускорение в левой части преобразуем к виду:

(1.29)

Подставляя в уравнгение движения, получим

(1.30)

Полученное уравнение отражает тот факт, что приращение кинетической энергии маятника равно убыли его потенциальной энергии в поле силы тяжести. Интегрируя уравнение, получим

(1.31)

Если принять, что потенциальная энергия маятника в положении равновесия равна нулю, то константа выражается через запасенную маятником энергию ( - угловая скорость маятника в положении равновесия):

(1.32)

Уравнение фазовой траектории окончательно запишется в виде:

(1.33)

При этом потенциальная и кинетическая энергии задаются выражениями

(1.34)

Используя (1.33), построим фазовый портрет системы (рис.5.7).

Рис. 5.7.Фазовый портрет колебания точки описывает возможность колебательного и вращательного движения массы

Отчетливо видны два типа фазовых траекторий, соответствующие двум типам движения: замкнутым (колебания) и незамкнутым (вращение вокрыг точки подвеса) траекториям

Замкнутые траектории, окружающие особые точки типа "центр" с координатами ( - целое число), соответствуют колебаниям маятника относительно устойчивого нижнего положения равновесия. Такие колебания имеют место, если энергия системы (см. рис. 5.7). При этом, если то колебания будут гармоническими, а фазовые траектории - эллипсами. Если то колебания будут негармоническими. При увеличении энергии, а, значит, и амплитуды колебаний осциллятора, их период будет возрастать, поскольку возвращающая сила в уравнении (1.28) меньше, чем в случае гармонического осциллятора.

Верхнему положению равновесия с координатами соответствуют особые точки типа "седло".

Фазовые кривые, проходящие через неустойчивые точки , "седла", соответствуют энергии и называются сепаратрисами. Они разделяют фазовое пространство на области с различным поведением. С увеличением энергии маятника его колебания от квазигармонических вблизи точек типа центр эволюционируют к нелинейным периодическим колебаниям вблизи сепаратрис. Дальнейшее увеличение энергии приведет к вращательному движению (движение вне сепаратрис). Малейшие отклонения энергии в ту или иную сторону от энергии движения по сепаратрисе приводят к качественно различным типам движения: колебательному или вращательному.

Таким образом, сепаратрисы разделяют фазовую плоскость на две области: область замкнутых траекторий (колебательный процесс) и область траекторий, приходящих из бесконечности и уходящих в бесконечность.

Отметим, что негармонические колебания нельзя характеризовать частотой", поскольку такие колебания являются, как правило, суперпозицией гармонических колебаний с различными частотами. Период же является по-прежнему одной из главных характеристик колебаний. Фазовый портрет не позволяет определить, как быстро движется точка Р по траектории. Однако период нелинейных колебаний математического маятника можно получить на основе приближенного решения уравнения (1.28).

Выводы:

Контрольные вопросы:

• Что такое фазовая плоскость?

• Что такое фазовая траектория?

• Что такое фазовый портрет колебаний?

• Какой вид имеет фазовый портрет гармонического осциллятора без потерь?

• Какой вид имеет фазовый портрет гармонического осциллятора с потерями?

• Что такое узел на фазовом портрете колебаний?

• Что такое седло на фазовом портрете колебаний?

• Что такое сепаратрисса на фазовом портрете колебаний?

• Как будет выглядеть фазовый портрет с усилением колебаний?

• Где используются фазовые портреты колебаний?

Лекция 6. Затухающие колебания. Вынужденные колебания. Резонанс.

Свободные незатухающие колебания являются идеализацией, моделью применимой на небольших временных интервалах. В реальных механических колебательных системах всегда присутствуют диссипативные силы (силы трения, силы вязкости), приводящие к уменьшению механической энергии системы из-за ее перехода в другие формы, например, в тепловую. Рассмотрим особенности колебательного движения при наличии диссипации.