Способы представления колебательных движений: Аналитический, табличный, графический, спектральный, векторные диаграммы, фазовый портрет

Гармонические колебания являются простейшей моделью колебательного движения достаточно часто встречающегося в действительности. Любое колебание может быть представлено как сумма гармонических колебаний.

Колебания по характеру взаимодействия с окружающей средой подразделяются на свободные затухающие, вынужденные, параметрические, связанные, в распределенных системах.:

Контрольные вопросы:

1. Определение колебательного процесса.

2. Опишите формы колебаний.

3. Каковы виды колебаний.

4. Опишите классификацию колебательных процессов.

5. Приведите характеристики колебательного процесса.

6. Каковы условия возникновения колебаний.

7. Опишите гармонические колебания.

8. Каковы способы представления колебательных движений.

9. Векторная диаграмма колебаний.

10. Что такое фазовая траектория, фазовый портрет?

Лекция 2. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения. Сложение взаимно перпендикулярных колебаний

Сложение гармонических колебаний одного направления

Если колеблющееся система или тело участвует в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты

воспользовавшись методом вращающегося вектора амплитуды.

Построим векторные диаграммы этих колебаний (рис. 2.1).

Рис. 2.1. Сложение колебаний с помощью векторной диаграммы

Taк как векторы A₁ и А₂ вращаются с одинаковой угловой скоростью ₀, то разность фаз (₂—₁) между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет:

В выражении амплитуда А и начальная фаза  соответственно задаются соотношениями:

(144.2)

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направле­нии и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (₂—₁) складываемых колебаний.

Проанализируем выражение (144.2) в зависимости от разности фаз (₂—₁):

1) ₂—₁ = ±2m (т=0, 1, 2, ...), тогда A=A₁+A₂, т. е. амплитуда результиру­ющего колебания А равна сумме амплитуд складываемых колебаний;

2) ₂—₁ = ±(2m+1) (т=0, 1, 2, ...), тогда A=|A₁–A₂|, т. е. амплитуда резуль­тирующего колебания равна разности амплитуд складываемых колебаний.

Биения

Для практики особый интерес представляет случай, когда два складываемых гар­монических колебания одинакового направления мало отличаются по частоте. В ре­зультате сложения этих колебаний получаются колебания с периодически изменяющей­ся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.

Пусть амплитуды складываемых колебаний равны А, а частоты равны  и +, причем <<. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Складывая эти выражения и учитывая, что во втором сомножителе /2<<, найдем

Результирующее колебание можно рассматривать как гармоническое с частотой , амплитуда А_б, которого изменяется по следующему периодическому закону:

Частота изменения А_б в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:

Период биений:

Характер зависимости показан на рисунке, где сплошные жирные линии дают график результирующего колебания, а огибающие их — график медленно меня­ющейся по уравнению амплитуды.

Определение частоты тона (звука определенной высоты биений между эталонным и измеряемым колебаниями — наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.

Рис. 2.2. Биения

Сложение колебаний с помощью векторов имеет большие преимущества перед аналитическими методами при сложении большого числа колебаний с одинаковыми частотами, например, при исследовании многолучевой интерференции.

Сложение взаимно перпендикулярных колебаний

Рассмотрим материальную точку, участвующую в двух взаимно перпендикулярных колебаниях по осям X и Y. Она будет двигаться по некоторой криволинейной траектории, форма которой зависит как от соотношения частот, так и от разности фаз обоих колебаний.

1) Пусть частоты складываемых колебаний одинаковы, а уравнения колебаний имеют вид

Рис. 2.3. Колебания в плоскости x0y

,

где: и– амплитуды складываемых колебаний вдоль осейX и Y;

–разность фаз складываемых колебаний.

Система представляет собой уравнение искомой траектории в параметрической форме.

Чтобы получить уравнение траектории в явном виде, исключим параметр t из системы. Для этого разделим каждое уравнение системы на соответствующую ему амплитуду и получим

Используя тригонометрическое тождество

,

для второго уравнения после подстановкииз первого уравнения получим

Или после преобразования

Из аналитической геометрии известно, что это уравнение эллипса с произвольно ориентированными осями, вписанного в прямоугольник со сторонами 2a и 2b, ограничивающего пространство, в котором совершаются колебания (рис. 2.3). Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Ориентация относительно осей зависит от разности фаз.

Кроме того, если А=В, то эллипс) вырождается в окружность. Такие колебания называются циркулярно поляризо­ванными колебаниями или колебаниями, поляризованными по кругу.

2) Рассмотрим частные случаи уравнения (2.2)

А) Пусть = 0, тогда cos = 1, sin = 0 и уравнение примет вид

, или

Это значит, что точка движется по прямой, совершая гармонические колебания с частотой  из первой четверти координатной плоскости в третью четверть (рис.2.4). Амплитуда такого колебания равна .

Рис. 2.4.

Б) Пусть , тогда cos = –1, sin = 0 и уравнение примет вид

или .

Это значит, что точка движется по прямой, совершая гармонические колебания с частотой  из второй четверти координатной плоскости в четвертую (рис.2.3 e). В данном случае имеем дело с линейно поляризованными колебаниями; Амплитуда такого колебания равна

Рис. 2.5.

В) Пусть , тогдаcos = 0, sin = 1 и уравнение (2.2) примет вид

.

То есть точка движется по эллипсу (рис.2.3.c), оси которого совпадают с осями координат, а полуоси равны a и b. При этом, если , то точка движется по часовой стрелке, если, то против часовой стрелки.

Рис. 2.6.

Г) Если частоты взаимно перпендикулярных колебаний отличаются на малую величину Δ, то можно считать, что они происходят с одинаковой частотой, а разность фаз медленно меняется по закону

.

В этом случае траектория будет медленно меняться, последовательно проходя все этапы, показанные на рис. 2.7.

Рис.2.7. Сложение колебаний с одинаковыми частотами

При разности фаз груз движется по часовой стрелке, а при- против часовой стрелки. Типичным примером двумерногоосциллятора (маятника) является электрон в атоме, который движется вокруг ядра по эллиптической орбите с периодом обращения T~10^-15 c Можно считать, что такой электрон одновременно совершает два взаимно-перпендикулярных колебания с частотой

3) Рассмотрим случай, когда частоты складываемых колебаний отличаются в два раза, например ,.

Система уравнений (1) примет вид

Используя формулу косинуса двойного угла, получим уравнение параболы (рис.2.8)

4) В общем случае, когда частоты взаимно перпендикулярных колебаний неодинаковы и кратны

,

то траектории результирующего движения имеют вид довольно сложных кривых, называемых фигурами Лиссажу. Эти фигуры вписаны в прямоугольник 2a2b, ограничивающий колебания по осям X и Y. При этом количество точек пересечения фигуры Лиссажу и оси X равно m, а количество точек пересечения оси Y равно n.

Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рисунке 2.9 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз .

Рис.2.10. Фигуры Лиссажу при разных соотношениях частот и фаз

По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко используемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.

Если кратность между частотами отсутствует, то траектории не являются замкнутыми и постепенно заполняют весь прямоугольник, напоминая нить в клубке.

Контрольные вопросы:

1. Сложение однонаправленных колебаний методом векторных диаграмм

2. Преимущества метода векторных диаграмм

3. Какова траектория точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях с одинаковыми периодами? Когда получается окружность? Прямая?

4. Как по виду фигур Лиссажу можно определить отношение частот складываемых колебаний?

5. Какие фигуры могут быть получены при сложении колебаний с одинаковыми частотами;

6. Какие фигуры могут быть получены при сложении колебаний с близкими но различными частотами

7. Что такое биения? Чему равна частота биений? Период?

8. Какова траектория точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях с одинаковыми периодами? Когда получается окружность? Прямая?

9. Как по виду фигур Лиссажу можно определить отношение частот складываемых колебаний?

10. Что такое биения? Чему равна частота биений? Период?

Лекция. 3. Спектральное представление колебательных процессов.

Обычной и естественной системой отсчета для нас является время. Мы наблюдаем, как развивается, то или иное событие во времени. Для наблюдения изменения во времени мгновенных значений величины какого-то электрического явления (или любого другого явления, переведенного в напряжение посредством надлежащего преобразователя) можно использовать осциллограф. Иными словами, мы используем осциллограмму для наблюдения формы сигнала во временной области. Частотная представление - альтернатива временной области.

На рис показано временное и частотное представление сложного сигнала, состоящего из двух частотных составляющих. В частотной области показан амплитуды каждой синусоидальной волны в спектре в зависимости от частоты. Как видно, в данном случае спектр состоит лишь из двух волн.

Рисунок 3.1. Связь между временной и частотной областью

Спектр – это набор синусоидальных волн, которые, будучи определенным образом, скомбинированы, дают изучаемый нами сигнал во временной области.

Теория Фурье гласит, что любое электрическое явление во временной области может быть представлено также одной или комбинацией синусоидальных волн с соответствующими частотами, амплитудами и фазами. То есть можно преобразовать сигнал во временной области в его эквивалент в частотной области. Использование модели гармонических колебаний позволяет описывать сложные периодические движения.

Периодические сигналы.

Еще в 1822 году французский физик и математик Жан Батист Жозеф Фурье в своей работе «Аналитическая теория теплоты» показал, что любая периодическая функция может быть представлена в виде суммы гармонических функций (то есть синусов и косинусов), причем частоты этих функций являются кратными основной частоте. Так, если период некоторой функции x(t) равен T, то эта функция может быть представлена в виде суммы (разложения Фурье):

где ω = 2π/T , коэффициенты Фурье рассчитываются по формулам

,

В общем случае эта сумма должна содержать бесконечно много слагаемых, однако в большинстве практически значимых случаев коэффициенты этого разложения достаточно быстро убывают с ростом номера k (и соответствующей частоты ω_k = k2π/T), поэтому практически всегда с достаточной степенью точности можно ограничиться относительно небольшим числом слагаемых. С разложением периодической функции хорошо знакомы музыканты, которые знают, что каждой ноте (основному тону), взятой на любом музыкальном инструменте соответствует целый набор кратных частот (обертонов). Набор этих колебаний с кратными частотами составляет тембр звука. Член ряда Фурье называется первой гармоникой. Если колебания среды носят синусоидальный характер, сигнал называют гармоническим или чистым. Несколько гармонических сигналов образуют совокупность, называемую сложным звуком. В этом случае чистый звук с наименьшей частотой называют основным тоном, а остальные ‑ обертонами. Если колебания носят непериодический произвольный характер, то такой звук называют шумом (рис.3.2).

Рис. 3.2.. Типовые колебания воздуха

На рис. 3-3 показана временная форма сложного сигнала.

Рисунок 3-3. Сложный сигнал во временной области

Рассмотрим примеры:

На рис. 3.4 изображены два синусоидальных колебания, частоты которых относятся как 1:5, а отношение амплитуд выбрано 5:1, и результат сложения этих колебаний:

и   .

 Рис. 3.4. Сложение двух колебаний (отношение частот 5:1, отношение амплитуд 1:3)

На рис.3.5 представлена сумма двух колебаний с одинаковой амплитудой, но несколько отличающимися частотами ; и сумма этих колебаний представляющее собой синусоидальное колебание с периодически изменяющейся амплитудой. Такую форму колебаний называют биениями.  

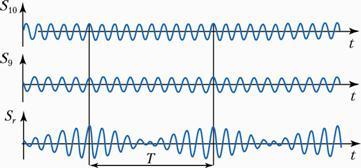
 Рис. 3.5. Сложение двух синусоидальных колебаний с равными амплитудами (соотношение частот 10:9).

Последовательность прямоугольных импульсов (рис.3.6) также можно представить в виде суммы простых синусоидальных колебаний. Это уже удается сделать с некоторым приближением, сложив три синусоиды S₁, S₃ и S₅. Получится кривая S_r. Большее приближение к последовательности прямоугольных импульсов может быть достигнуто, если увеличить число слагаемых синусоид S₇, S₉ и т. д.  

Рис.3.6. Последовательность прямоугольных импульсов, три первые гармоники и их сумма

 Рис. 3.7. Представление прямоугольных импульсов с помощью гармонических функций

Разложение в ряд Фурье периодических функций

Таблица1

График f(t)	Разложение в ряд Фурье функции f(t)	Примечание
		k=1,3,5,...
		k=1,3,5,...
		k=1,3,5,...
		k=1,2,3,4,5
		k=1,3,5,...
		k=1,2,3,4,5
		S=1,2,3,4,..
		k=1,2,4,6,..

В соответствии с теорией рядов Фурье точное равенство негармонического сигнала сумме гармоник имеет место только при бесконечно большом числе гармоник. Расчет гармонических составляющих на ЭВМ позволяет анализировать любое число гармоник, которое определяется целью расчета, точностью и формой негармонического воздействия. Если длительность сигнала t независимо от его формы много меньше периода T, то амплитуды гармоник будут убывать медленно, и для более полного описания сигнала приходится учитывать большое число членов ряда. Эту особенность можно проследить для сигналов, представленных в таблице 2 - 5 и 6, при выполнении условия τ <<T. Если негармонический сигнал по форме близок к синусоиде (например, сигналы 2 и 3 в табл.2), то гармоники убывают быстро, и для точного описания сигнала достаточно ограничиться тремя - пятью гармониками ряда.

Рисунок 3.8 - Спектральное представление ПППИ: а) временная диаграмма; б) спектральная диаграмма амплитуд; в) спектральная диаграмма фаз

Как видно из формулы ширина спектра ПППИ зависит только от длительности импульса и не зависит от его периода.

Преобразование Фурье также может быть осуществлено и из частотной области во временную. В этом случае, опять же, теоретически нам надо знать все спектральные составляющие в диапазоне частот до ± бесконечности. На самом же деле, производя измерения только в той области частот, в которой содержится наибольшая часть энергии сигнала, можно получить вполне приемлемые результаты. При преобразовании Фурье из частотной области очень важно знать фазу индивидуальных составляющих. Например, прямоугольный периодический сигнал, переведенный в частотную область и обратно, может превратиться в пилообразный, если не были определены фазы.

Спектр сигнала — в радиотехнике это результат разложения сигнала на более простые в базисе ортогональные функции. В качестве разложения обычно используются преобразование Фурье, разложение по функциям Уолша, вейвлет-преобразование и др.

В радиотехнике в качестве базисных функций используют синусоидальные функции. Это объясняется рядом причин:

• функции , являются простыми и определены при всех значениях t, являются ортогональными и составляют полный набор при кратном уменьшении периода;

• гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через линейную систему с постоянными параметрами, могут только изменяться амплитуда и фаза;

• для гармонических функций имеется математический аппарат комплексного анализа;

• гармоническое колебание легко реализуемо на практике.

Кроме гармонического ряда Фурье применяются и другие виды разложений: по функциям Уолша, Бесселя, Хаара, Лежандра, полиномам Чебышева и др.

В цифровой обработке сигналов для анализа применяются дискретные преобразования: Фурье, Хартли, вейвлетные и др.

Причины использования спектрального представления. Расчет физических процессов в частотном представлении имеет огромные преимущества для линейных процессов, поскольку позволяет заменить сложную процедуру решения дифференциальных уравнений решением алгебраических уравнений. Сигнал может быть разложен на отдельные синусоидальные волны, или спектральные составляющие, которые затем можно исследовать независимо друг от друга. Каждая такая волна описывается амплитудой и фазой. Если сигнал, который мы хотим исследовать, - периодический (как в нашем случае), то по теории Фурье составляющие его синусоидальные волны будут разнесены в частотной области на 1/Т, где Т – это период сигнала. Измерения в частотной области способны показать, сколько энергии имеется на каждой конкретной частоте.

Зачем, собственно, нужно считать спектры сигналов?

Во-первых, это позволяет по-новому взглянуть на сигнал, лучше понять его природу, найти характерные частоты сигнала (если их несколько, то по виду самого сигнала это может быть затруднительно). Например, складывая две синусоиды можно добиться весьма разнообразных форм сигнала. Посмотрев только на форму, не всегда можно понять, что такой сигнал можно представить как всего две синусоиды. На спектре это видно.

Если в спектре присутствует несколько пиков, а большая часть составляющих равна 0, то можно добиться грандиозного сжатия информации. Всего несколько чисел – положение пиков и амплитуды соответствующих гармоник, но в них практически вся информация о свойствах сигнала.

При обработке медицинских сигналов требуется строить диагностические критерии, признаки того или иного заболевания. Расчет спектральных характеристик (частот, амплитуд гармоник, скорости спадания амплитуды с ростом частоты и т.д) – один из способов их поиска.

Еще одним приложением спектрального анализа является фильтрация сигналов.

Анализ частоты, амплитуды и фазы сигнала, дающих полную информацию о сигнале, называется векторным анализом сигнала.

Анализ сигнала не включающий определения фазовых соотношений между синусоидальными составляющими называется спектральным анализом.

У частотной области есть свои плюсы. Частотная область гораздо удобнее в плане измерений. Те, кто занимаются беспроводной связью, заинтересованы в определении внеполосного и паразитного излучения. Сотовые системы должны проверяться на наличие гармоник несущего сигнала, которые могут вносить помехи в работу других систем, оперирующих на той же частоте, что и гармоники. Инженеры часто обеспокоены искажением сообщений, транслирующихся с модуляцией несущего сигнала. Интермодуляция третьего порядка (когда две составляющие сложного сигнала, модулируют друг друга) может причинить много проблем, поскольку компоненты искажения могут попасть в интересуемую полосу частот и не будут надлежащим образом отфильтрованы. Наблюдение за спектром – еще одна важная сторона измерений в частотной области. Государственные регулирующие структуры распределяют различные частоты для различных радио-служб: телевизионное и радиовещание, сотовая связь, связь правоохранительных органов и спасательных служб, а также множество иных организаций. Каждая служба должна работать только на определенной для нее частоте в пределах выделенной полосы канала. Для усилителей и других компонентов систем ключевым параметром является количество энергии сигнала, просачивающейся в соседние каналы и порождающей интерференцию. Нежелательное излучение, будучи передано в эфир или по проводам, может затруднить работу других систем. Означает ли это, что измерения во временной области можно вообще не проводить? Временная область является предпочтительной для многих измерений, а для некоторых является единственно возможной. К примеру, только во временной области можно измерить длительность фронта и спада импульса, выбросы и биения.

Непериодические сигналы.

Непериодические сигналы можно представить в виде интеграла синусоидальных сигналов с непрерывным спектром частот. Например, спектральное разложение идеального импульса (единичной мощности и нулевой длительности) имеет составляющие всего спектра частот, от - ∞ до + ∞ (см. рис.3.9).

Рис.3.9. Спектральное представление идеального импульса.

Чтобы представить в виде гармоник непериодический сигнал не на конечном интервале, а на всей оси, необходимо использовать множество гармоник с непрерывным набором частот. Такое представление можно записать следующим образом:

. (5)

То есть суммируются синусоиды с разными частотами, у каждой своя амплитуда и начальная фаза. Каждая составляющая синусоида называется также гармоникой, а набор всех гармоник называют спектральным разложением исходного сигнала. Формулы для краткости и удобства аналитических расчетов принято писать в комплексной форме:

, . (10)

Здесь , то есть действительная часть этой величины есть, а мнимая есть. Эти выражения называютпрямым преобразованием и обратным преобразованием Фурье.

Техника нахождения спектра любого исходного сигнала хорошо известна. Для некоторых сигналов, которые хорошо описываются аналитически (например, для последовательности прямоугольных импульсов одинаковой длительности и амплитуды), спектр легко вычисляется на основании формул Фурье. Для сигналов произвольной формы, встречающихся на практике, спектр можно найти с помощью специальных приборов - спектральных анализаторов, которые измеряют спектр реального сигнала и отображают амплитуды составляющих гармоник на экране или распечатывают их на принтере. Искажение передающим каналом синусоиды какой-либо частоты приводит в конечном счете к искажению передаваемого сигнала любой формы, особенно если синусоиды различных частот искажаются неодинаково. Если это аналоговый сигнал, передающий речь, то изменяется тембр голоса за счет искажения обертонов - боковых частот. При передаче импульсных сигналов, характерных для компьютерных сетей, искажаются низкочастотные и высокочастотные гармоники, в результате фронты импульсов теряют свою прямоугольную форму (рис. 3.10). Вследствие этого на приемном конце линии сигналы могут плохо распознаваться.

Рис.3.10. Искажение импульсов в линии

Линия связи искажает передаваемые сигналы из-за того, что ее физические параметры отличаются от идеальных. Так, например, медные провода всегда представляют собой некоторую распределенную по длине комбинацию активного сопротивления, емкостной и индуктивной нагрузки (см. рис.). В результате для синусоид различных частот линия будет обладать различным полным сопротивлением, а значит, и передаваться они будут по-разному. Волоконно-оптический кабель также имеет отклонения, мешающие идеальному распространению света. Если линия связи включает промежуточную аппаратуру, то она также может вносить дополнительные искажения, так как невозможно создать устройства, которые бы одинаково хорошо передавали весь спектр синусоид, от нуля до бесконечности. Кроме искажений сигналов, вносимых внутренними физическими параметрами линии связи, существуют и внешние помехи, которые вносят свой вклад в искажение формы сигналов на выходе линии. Эти помехи создают различные электрические двигатели, электронные устройства, атмосферные явления и т. д. Несмотря на защитные меры, предпринимаемые разработчиками кабелей и усилительно-коммутирующей аппаратуры, полностью компенсировать влияние внешних помех не удается. Поэтому сигналы на выходе линии связи обычно имеют сложную форму, по которой иногда трудно понять, какая дискретная информация была подана на вход линии.