
- •2. Анализ систем массового обслуживания
- •2.1. Классификация систем
- •2.2. Система обслуживания м/м/1.
- •2.4. Системы обслуживания, зависящие от состояний.
- •2.5. Система обслуживания m/g/1.
- •2.6. Упрощенный вывод формулы для е(n) системы m/g/1
- •2.7. Система обслуживания g/m/1.
- •2.8. Системы обслуживания с относительными приоритетами.
- •Согласно формуле Литтла , (2.86)
2.6. Упрощенный вывод формулы для е(n) системы m/g/1
Строгий вывод формулы для E(n) через производящую функцию, как видно, довольно сложен. Проще E(n) можно получить из (2.42).
Возведём
(2.42) в квадрат, возьмём математическое
ожидание от обеих частей и положим
![]() :
:
![]() .
(*)
.
(*)
При
![]() из (2.42) следует
из (2.42) следует![]() .
.
Кроме
того:
![]() и
и![]() - оба равенства следуют из определенияU(n).
- оба равенства следуют из определенияU(n).
Будем
считать, что
![]() и
и![]() независимы, тогда
независимы, тогда
![]() .
.
С
учетом сделанных замечаний формулу (*)
перепишем в виде:
![]()
Учтем
также, что
![]() т. к. случайные величиныn
и
независимы. Теперь
т. к. случайные величиныn
и
независимы. Теперь
![]() ,
,
откуда
![]() .
.
Т.к.
![]() ,
то дляE(n)
окончательно запишем
,
то дляE(n)
окончательно запишем
![]() ,
,
что совпадает с (2.66)
Здесь
![]() - дисперсия числа клиентов, поступающих
в течение времени обслуживания.
- дисперсия числа клиентов, поступающих
в течение времени обслуживания.
Найдём
![]() .
По определению дисперсии
.
По определению дисперсии
![]() .
(2.67)
.
(2.67)
Поток
заявок на обслуживание пуассоновский,
поэтому для
![]() используем выражение (2.62), а
используем выражение (2.62), а![]() ,
поэтому
,
поэтому
![]() .
(2.68)
.
(2.68)
Изменим порядок интегрирования и суммирования с учётом следующих соотношений:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В последних трех формулах использованы свойства распределения Пуассона. Теперь (2.68) преобразуется к виду
![]() .
.
Если в последней формуле учесть, что
![]() ,
,
![]() ,
,
то
для
![]() можно окончательно записать
можно окончательно записать
![]() ,
(2.69)
,
(2.69)
где
![]() - дисперсия распределения времени
обслуживания.
- дисперсия распределения времени
обслуживания.
Подставим теперь (2.69) в (2.66):
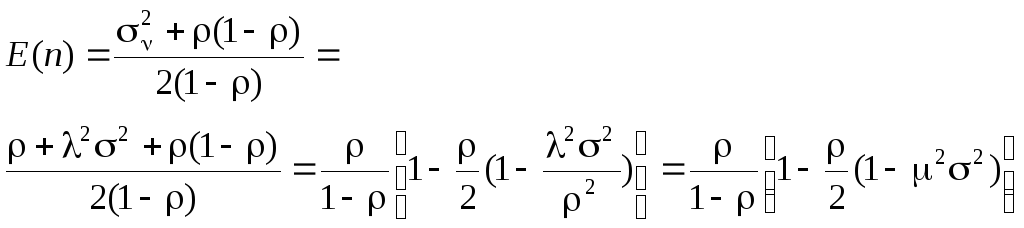 ,
,
т.
е.
![]() .
(2.70)
.
(2.70)
Формула (2.70) называется формулой Поллячека-Хинчина. Из формулы Литтла
![]() .
(2.71)
.
(2.71)
Здесь
![]() - среднее время обслуживания.
- среднее время обслуживания.
В
системе M/M/1
время обслуживания распределено
экспоненциально. Дисперсия этого
распределения
![]() .
Подставляя в (2.70), получаем:
.
Подставляя в (2.70), получаем:![]() ,
что совпадает с полученным ранее.
,
что совпадает с полученным ранее.
Для
системы M/D/1
все клиенты требуют одного времени
обслуживания
![]() ,
при этом
,
при этом![]() .
Тогда:
.
Тогда:
![]() ,
(2.72)
,
(2.72)
![]() .
.
Можно считать, что система M/D/1 - это частный случай M/M/1 с наименьшей длиной очереди и задержкой.
В заключение найдем среднее время ожидания E(W) для M/G/1:
![]() .
.
Подставим сюда E(T) из (2.71):
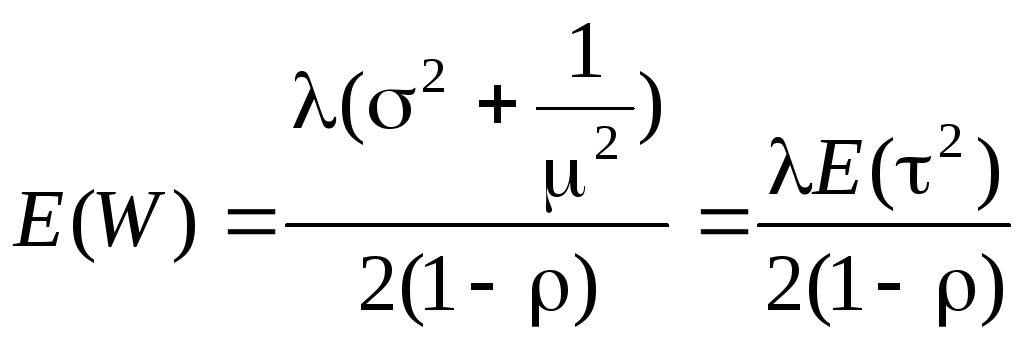 ,
(2.73)
,
(2.73)
где
![]() - второй момент распределения времени
обслуживания.
- второй момент распределения времени
обслуживания.
2.7. Система обслуживания g/m/1.
Рассматриваемая
система имеет один обслуживающий прибор
при дисциплине обслуживания FIFO.
Согласно описанной выше классификации
систем массового обслуживания здесь
предполагается, что промежутки времени
между поступлениями распределены
независимо с некоторой плотностью
![]() и средним значением
и средним значением![]() .
Время обслуживания распределено по
экспоненциальному закону при средней
интенсивности обслуживания.
Будем рассматривать только установившийся
режим.
.
Время обслуживания распределено по
экспоненциальному закону при средней
интенсивности обслуживания.
Будем рассматривать только установившийся
режим.
Ключевым понятием при описании системы, как и раньше, является состояние системы, где под состоянием понимается число клиентов в системе в некоторый фиксированный момент времени. Диаграмма состояний системы представлена на рис.2.17.
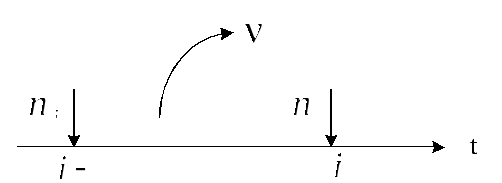
Рис.2.17. К определению состояния системы G/M/1
На рис.2.17 показана последовательность моментов поступления требований, отождествляемая с последовательностью точек временной оси, порождающей марковскую цепь с дискретными состояниями. Здесь введены следующие обозначения:
![]() -
число клиентов в системе в момент
поступления
j-го
требования на обслуживание,
-
число клиентов в системе в момент
поступления
j-го
требования на обслуживание,
![]() -
число клиентов, обслуженных между
поступлением j-1
и j-го
требования.
-
число клиентов, обслуженных между
поступлением j-1
и j-го
требования.
Согласно рисунку можно записать
![]() .
(2.74)
.
(2.74)
Предполагая,
что установившийся режим работы системы
существует (в работе [4] показано, что
для этого необходимо выполнение условия
![]() ,
где, как обычно,
,
где, как обычно,![]() ), вероятностьk-го
состояния системы определим как
), вероятностьk-го
состояния системы определим как
![]() .
(2.75)
.
(2.75)
Определим теперь для рассматриваемой цепи вероятности перехода из одного состояния в другое в виде
![]() .
(2.76)
.
(2.76)
По
сути дела, вероятность перехода вида
(2.76) есть вероятность того, что за
промежуток времени между поступлениями
будет обслужено
![]() требование. Из рис. 2.17 и определения
(2.76) следует, что число находящихся в
системе требований в промежутке времени
между поступлениями требованийj-1
и j
не
может быть больше, чем
требование. Из рис. 2.17 и определения
(2.76) следует, что число находящихся в
системе требований в промежутке времени
между поступлениями требованийj-1
и j
не
может быть больше, чем
![]() .
Поэтому
.
Поэтому![]() при
при![]() ,
т.е. переход из состоянияl
в состояние k
невозможен. На рис.2.18 представлена
диаграмма вероятностей переходов
марковской цепи, где указаны только
переходы из состояния l.
,
т.е. переход из состоянияl
в состояние k
невозможен. На рис.2.18 представлена
диаграмма вероятностей переходов
марковской цепи, где указаны только
переходы из состояния l.
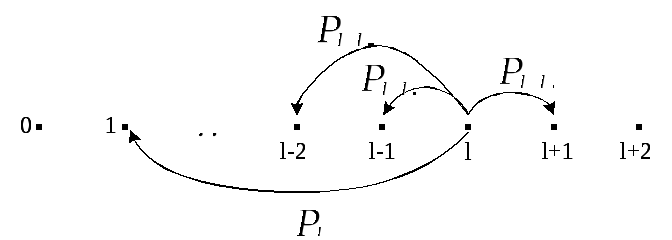
Рис.2.18. Диаграмма вероятностей переходов марковской цепи для системы G/M/1
Если бы вероятности возможных переходов из одного состояния в другое были найдены, то, как показано в [4], для случая установившегося режима работы системы собственно вероятности состояний, введенные формулой (2.75), могли бы быть найдены из решения системы линейных алгебраических уравнений, матричная форма записи которых имеет вид
![]() ,
(2.77)
,
(2.77)
где:
![]() - матрица-строка вероятностей состояний,
размерность которой определяется
интересующим нас набором состояний,
- матрица-строка вероятностей состояний,
размерность которой определяется
интересующим нас набором состояний,
P
– матрица,
элементы которой совпадают с вероятностями
![]() перехода за один шаг.
перехода за один шаг.
Задача состоит в том, чтобы найти эти вероятности перехода. Для этого рассмотрим четыре области на плоскости (l, k), изображенные на рис.2.19.
Для
области
![]() ,
где для индексовl
и
k
справедливо соотношение
,
где для индексовl
и
k
справедливо соотношение
![]() ,
выше было выяснено, что здесь
,
выше было выяснено, что здесь![]() .
.
В
области
![]() для индексовl
и
k
соотношение определяется неравенствами
для индексовl
и
k
соотношение определяется неравенствами
![]() ,
что соответствует тому случаю, когда
требование
,
что соответствует тому случаю, когда
требование
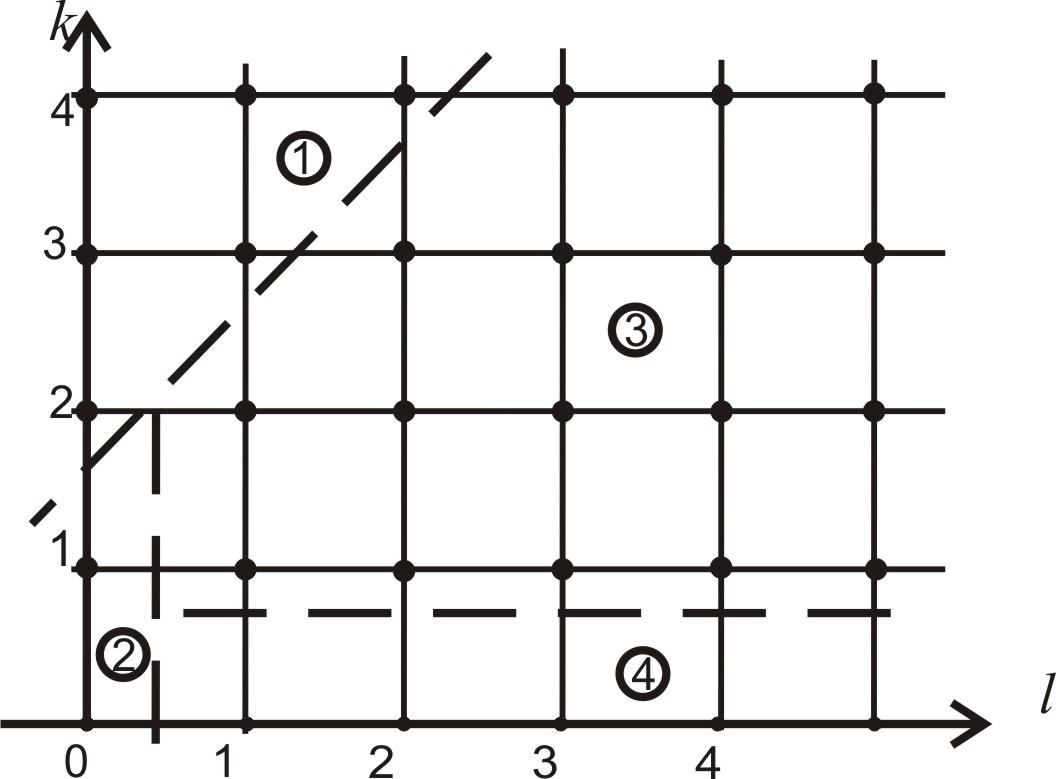
Рис.2.19.
Границы изменения индексов l
и
k
при выводе формул для
![]() .
.
не
ждет, а сразу поступает на обслуживание.
(Последняя единица в системе неравенств
характеризует то, что мы рассматриваем
однолинейную систему). За время между
поступлениями требований закончится
обслуживание
![]() требований. Но в области
требований. Но в области![]() l=0
и
l=0
и
![]() ,
поэтому ни одно требование не покинет
систему. Т.к. время обслуживания
распределено экспоненциально, вероятность
этого события равна
,
поэтому ни одно требование не покинет
систему. Т.к. время обслуживания
распределено экспоненциально, вероятность
этого события равна![]() .
Поэтому для единственной в этой области
вероятности
.
Поэтому для единственной в этой области
вероятности![]() можно записать
можно записать
![]() ,
,
![]() (2.78)
(2.78)
где
![]() - плотность вероятности интервалов
между приходом требований.
- плотность вероятности интервалов
между приходом требований.
Теперь
рассмотрим область
![]() ,
которая характеризуется неравенствами
,
которая характеризуется неравенствами![]() .
В этой области сосредоточены вероятности
.
В этой области сосредоточены вероятности![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и т.д. Это – случай, когда обслуживающая
линия занята на протяжении всего
промежутка времени между поступающими
требованиями, и они попадают в накопитель
для ожидания. Т.к. время обслуживания в
данной системе распределено экспоненциально,
то число обслуживаний за время промежутка
между поступающими требованиями
распределено по закону Пуассона с
параметром
(это будет, естественно, условная
вероятность). Если ввести обозначение,
что А – событие, состоящее в том, что на
протяжении интервала времени
t
линия занята, то можно записать
и т.д. Это – случай, когда обслуживающая
линия занята на протяжении всего
промежутка времени между поступающими
требованиями, и они попадают в накопитель
для ожидания. Т.к. время обслуживания в
данной системе распределено экспоненциально,
то число обслуживаний за время промежутка
между поступающими требованиями
распределено по закону Пуассона с
параметром
(это будет, естественно, условная
вероятность). Если ввести обозначение,
что А – событие, состоящее в том, что на
протяжении интервала времени
t
линия занята, то можно записать
![]() .
(2.79)
.
(2.79)
Как
указывалось выше, чтобы перейти из
состояния
l
в состояние k,
необходимо, чтобы за время t
было обслужено ровно
![]() требований. Имея это в виду, для
требований. Имея это в виду, для![]() запишем
запишем![]() .
.
(2.80)
Итак,
в области
![]()
![]() - это вероятность обслуживания
- это вероятность обслуживания![]() требований за промежуток времени, равный
промежутку, когда обслуживающая линия
остается занятой.
требований за промежуток времени, равный
промежутку, когда обслуживающая линия
остается занятой.
Для
области
![]() соотношение между индексамиl
и k
имеет
вид:
соотношение между индексамиl
и k
имеет
вид:
![]() .
Здесь ситуация такова, что поступающее
требование застает требование на
обслуживании иl
-1
требований в очереди. Поступившее
требование встает в очередь на
обслуживание. Итак, в системе становится
l
требований, и предположим, что все их
надо обслужить за время
.
Здесь ситуация такова, что поступающее
требование застает требование на
обслуживании иl
-1
требований в очереди. Поступившее
требование встает в очередь на
обслуживание. Итак, в системе становится
l
требований, и предположим, что все их
надо обслужить за время
![]() ,
где
,
где![]() - время между поступающими требованиями.
Если положить
- время между поступающими требованиями.
Если положить![]() ,
то с учетом того, что процесс обслуживания
пуассоновский
,
то с учетом того, что процесс обслуживания
пуассоновский
![]() ,
и тогда согласно вышеизложенному
,
и тогда согласно вышеизложенному
![]() .
(2.81)
.
(2.81)
Таким образом, выражения (2.77), (2.78), (2.80) и (2.81) дают описание вероятностей перехода и вероятностей состояний для системы G/M/1.
В фундаментальной работе [4] по теории массового обслуживания, показано, что для вероятностей состояния системы справедлив следующий результат
![]() (2.82)
(2.82)
где
- единственное решение уравнения
![]() в области
в области![]() .
.
Там
же показано, что система G/M/1
приводит к геометрическому распределению
числа требований (клиентов) в моменты
поступления нового требования и
распределение времени ожидания имеет
такую же форму как распределение времени
ожидания в системе М/М/1 при выполнении
условия
![]() .
.
