
- •2. Анализ систем массового обслуживания
- •2.1. Классификация систем
- •2.2. Система обслуживания м/м/1.
- •2.4. Системы обслуживания, зависящие от состояний.
- •2.5. Система обслуживания m/g/1.
- •2.6. Упрощенный вывод формулы для е(n) системы m/g/1
- •2.7. Система обслуживания g/m/1.
- •2.8. Системы обслуживания с относительными приоритетами.
- •Согласно формуле Литтла , (2.86)
2.4. Системы обслуживания, зависящие от состояний.
Пусть есть система с очередью, в которой интенсивности поступлений и обработки зависят от состояния системы. Напомним, что под состоянием системы понимается количество клиентов n, находящихся в системе, включая клиента, на обслуживании. Предположение о зависимости процессов поступления и ухода от состояния приводит к понятию процессов размножения и гибели.
Рассмотрим систему, представленную на рис. 2.11.

Рис. 2.11. Система, зависящая от состояний.
Пусть
поступления в систему – пуассоновские
с интенсивностью
![]() ,
а распределение времени обслуживания
– экспоненциальное с параметром
,
а распределение времени обслуживания
– экспоненциальное с параметром![]() .
Определим для системы, находящейся в
состоянииn,
вероятность одного поступления за
интервал времени
.
Определим для системы, находящейся в
состоянииn,
вероятность одного поступления за
интервал времени
![]() в виде
в виде![]() .
Вероятность отсутствия поступлений,
соответственно, запишется как
.
Вероятность отсутствия поступлений,
соответственно, запишется как![]() .
Будем также предполагать, что последействие
отсутствует, т.е. вероятность того, что
происходит в интервале
.
Будем также предполагать, что последействие
отсутствует, т.е. вероятность того, что
происходит в интервале![]() ,
не зависит от того, что происходит на
других интервалах.
,
не зависит от того, что происходит на
других интервалах.
Процесс
ухода клиентов определяется аналогичными
вероятностями на интервале
![]() :
:![]() и
и![]() .
.
Рассмотренная
выше система, когда
![]() и
и![]() ,
является частным случаем рассматриваемой.
,
является частным случаем рассматриваемой.
Объединяя
два процесса и устремляя
![]() ,
для состояния статистического равновесия,
повторяя вышеприведенные рассуждения,
можно записать
,
для состояния статистического равновесия,
повторяя вышеприведенные рассуждения,
можно записать
![]() .
(2.22)
.
(2.22)
Уравнение равновесия (2.22) может быть получено путем приравнивания интенсивностей уходов из состояния n к интенсивности приходов в состояние n (см. пунктирную область около состояния n на рис.2.12).
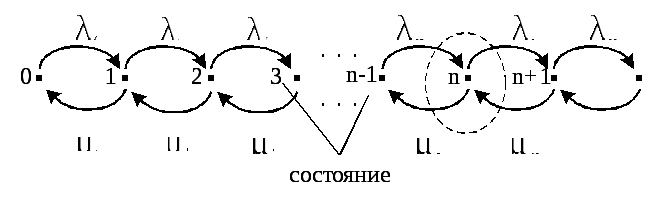
Рис.2.12. Состояние равновесия по уравнению (2.22).
Решение уравнения (2.22) можно, как и выше, искать в виде
![]() ,
(2.23)
,
(2.23)
что приводит к
 .
(2.24)
.
(2.24)
Вероятность
![]() определяется из условия нормировки
определяется из условия нормировки![]() .
ЕслиN
(число клиентов в очереди) конечно, то
система всегда стабильна. При бесконечной
очереди (
.
ЕслиN
(число клиентов в очереди) конечно, то
система всегда стабильна. При бесконечной
очереди (![]() )
стабильность гарантируется при
)
стабильность гарантируется при![]() >0.
>0.
Приведем теперь примеры использования обсужденной модели системы массового обслуживания.
Система М/М/2.
Рассмотрим систему, изображенную на рис.2.13.
На
входе системы действует пуассоновский
поток пакетов данных с интенсивностью
.
Длина пакетов предполагается случайной
величиной с экспоненциальным распределением
со средним значением
![]() секунд.
секунд.
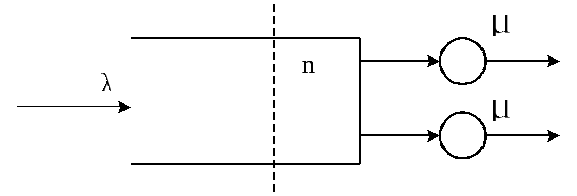
Рис.2.13. Система М/М/2.
Вероятность
завершения обслуживания за интервал
![]() влюбом
канале
равна
влюбом
канале
равна
![]() ,
а вероятностьодного
завершения обслуживания в системе -
,
а вероятностьодного
завершения обслуживания в системе -
![]() .
Таким образом, система М/М/2 может
рассматриваться как система, зависящая
от состояния, потому, что
.
Таким образом, система М/М/2 может
рассматриваться как система, зависящая
от состояния, потому, что
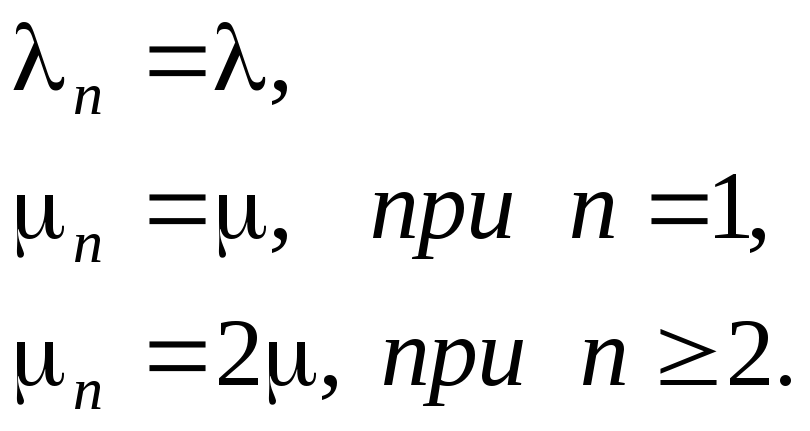
Из (2.24)
![]() ,
(2.25)
,
(2.25)
где
![]() .
.
Вероятность
Р0
найдем для случая бесконечного накопителя
из условия
![]() .
.
Подставим
(2.25) в условие нормировки:
![]() .
Теперь
.
Теперь![]() .
И, наконец:
.
И, наконец:
![]() .
(2.26)
.
(2.26)
Формула (2.25) запишется как
![]() ,
,
![]() .
(2.27)
.
(2.27)
Найдем среднюю занятость системы
![]() .
.
При
выводе формулы (2.13) было получено
![]() .
С учетом этого результата
.
С учетом этого результата
![]() .
(2.28)
.
(2.28)
Сравним
занятость систем М/М/1 и М/М/2. Напомним,
что
![]() ,
где
,
где![]() .
С учетом соотношения для
можно утверждать, что средняя занятость
системы М/М/2 всегда меньше.
.
С учетом соотношения для
можно утверждать, что средняя занятость
системы М/М/2 всегда меньше.
Среднее время задержки определим по формуле Литтла:
![]() ,
где
,
где
![]() .
(2.29)
.
(2.29)
Для
сравнения:
![]() ,
где
,
где![]() .
Теперь видно, что всегда
.
Теперь видно, что всегда
![]() .
.
На
рис.2.14 приведены зависимости нормированной
задержки от коэффициента нагрузки для
трех систем:
![]() ,
М/М/2 и системы
,
М/М/2 и системы![]() с удвоенной интенсивностью обслуживания.
с удвоенной интенсивностью обслуживания.
Из
сравнения зависимостей следует, что
добавление обслуживающей линии уменьшает
время задержки и, естественно, увеличивает
производительность системы. Но система
![]() будет лучше, чем М/М/2, т.е. удвоение
пропускной способности лучше, чем
добавление второй линии (если это
оправдано стоимостью и надежностью
оборудования).
будет лучше, чем М/М/2, т.е. удвоение
пропускной способности лучше, чем
добавление второй линии (если это
оправдано стоимостью и надежностью
оборудования).
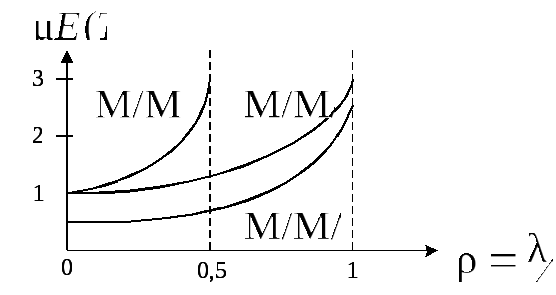
Рис.2.14. Сравнение нормированной задержки трех систем.
Для
системы М/М/2 максимально возможная
производительность составляет величину
![]() ,
но она никогда не может быть достигнута,
т.к. с вероятностьюР0
система
пустая и с вероятностью Р1
используется
только одна линия. Поэтому средняя
производительность определяется как
,
но она никогда не может быть достигнута,
т.к. с вероятностьюР0
система
пустая и с вероятностью Р1
используется
только одна линия. Поэтому средняя
производительность определяется как
![]() .
(2.30)
.
(2.30)
В
справедливости последнего знака
равенства легко убедиться, подставив
в (2.30) Р0
и Р1
из
(2.26) и (2.27). С учетом (2.30) величину
![]() можно рассматривать как отношение
средней производительности к максимальной.
можно рассматривать как отношение
средней производительности к максимальной.
Система
![]() .
.
Здесь обслуживающая линия доступна любому клиенту, поступающему в систему. Поэтому очередей и блокировок не возникает, и для данной системы
![]() .
.
Из
(2.25)
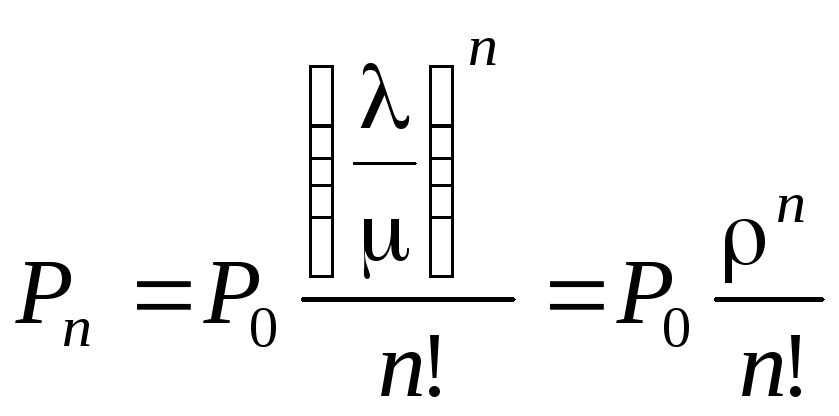 ,
где
,
где![]() .
.
Из
условия нормировки
![]() .
С учетом того, что
.
С учетом того, что![]() ,
дляР0
получаем
,
дляР0
получаем
![]() .
Если данное значение вернуть в формулу
дляРn
, то получится
.
Если данное значение вернуть в формулу
дляРn
, то получится
![]() - это формула Пуассона.
- это формула Пуассона.
Среднее
количество клиентов в системе:![]() (результат был получен выше при
исследовании распределения Пуассона).
Итак
(результат был получен выше при
исследовании распределения Пуассона).
Итак
![]() .
(2.31)
.
(2.31)
Сравнение
с
![]() показывает, что
показывает, что![]() <
<![]() .
Это сравнение говорит о целесообразности
увеличения числа обслуживающих линий,
либо о необходимостиуправления
интенсивностью
входящего потока.
.
Это сравнение говорит о целесообразности
увеличения числа обслуживающих линий,
либо о необходимостиуправления
интенсивностью
входящего потока.
Производительность
системы ,
определенная «по входу» равна ,
т.к. для всех n
выполняется
![]() .
.
Средняя задержка
![]() .
(2.32)
.
(2.32)
Это
очевидно, т.к. очереди нет, и время
задержки равно среднему времени
обслуживания
![]() .
Производительность системы можно
рассчитать и «по выходу» через
интенсивность обслуживания с учетом
.
Производительность системы можно
рассчитать и «по выходу» через
интенсивность обслуживания с учетом![]()
![]() ,
(2.33)
,
(2.33)
что совпадает с производительностью, определенной «по входу».
Система с «нетерпеливыми» клиентами.
Это - система с управлением входным потоком.
Здесь
![]() и
и![]() .
Доступна одна обслуживающая линия, и,
когда очередь становится большой –
клиенты уходят. Для передачи пакетов
это означает, что контроллер системы
либо отводит новые поступления, либо
блокирует систему, что приводит к
уменьшению интенсивности поступлений.
.
Доступна одна обслуживающая линия, и,
когда очередь становится большой –
клиенты уходят. Для передачи пакетов
это означает, что контроллер системы
либо отводит новые поступления, либо
блокирует систему, что приводит к
уменьшению интенсивности поступлений.
Нетрудно убедиться, что из общей формулы (2.24) легко для данной системы получить
![]() ,
где
,
где
![]() .
Значит в этой системе
.
Значит в этой системе![]() ,
и
,
и![]() .
Следовательно
.
Следовательно
![]() .
.
Производительность системы, определенная «по входу», запишется как
![]() .
.
С
учетом того, что
![]() последнее выражение примет вид
последнее выражение примет вид
![]() .
(2.34)
.
(2.34)
Этот
результат можно получить и по-другому,
если учесть, что для однолинейной системы
с интенсивностью обслуживания
производительность равна
![]() .
Но здесь
.
Но здесь![]() ,
что и дает результат (2.34).
,
что и дает результат (2.34).
Зная
![]() и
можно найти нормированное среднее время
задержки
и
можно найти нормированное среднее время
задержки
![]()
![]() ,
,
![]() . (2.35)
. (2.35)
При
![]()
![]() ,
(с учетом
,
(с учетом![]() ),
т.е. задержка приближенно равна времени
обслуживания и
),
т.е. задержка приближенно равна времени
обслуживания и![]() .
.
Система
остается стабильной и при больших ,
т.к. существует управление потоком. При
этом растет средняя занятость системы
![]() и наиболее вероятны состояния с большими
значениямиn.
и наиболее вероятны состояния с большими
значениямиn.
Система M/M/N/0.
Это
частный случай системы
![]() с конечным числом обслуживающих линий
и без мест для ожидания (без накопителя)
– см. рис.2.15.
с конечным числом обслуживающих линий
и без мест для ожидания (без накопителя)
– см. рис.2.15.
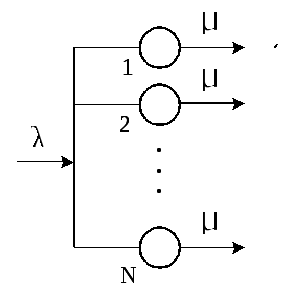
Рис. 2.15. Система M/M/N/0.
Здесь
![]() и
и![]() .
Приn=N
все
поступления блокируются. Мест для
ожидания нет и поэтому – это система с
потерями. Данная система является
базовой моделью для анализа телефонных
станций.
.
Приn=N
все
поступления блокируются. Мест для
ожидания нет и поэтому – это система с
потерями. Данная система является
базовой моделью для анализа телефонных
станций.
Для
системы
![]() было получено
было получено![]() ,
где
,
где![]() .
Здесь условие нормировки имеет вид
.
Здесь условие нормировки имеет вид![]() .
Подставляя сюда
.
Подставляя сюда![]() получаем
получаем
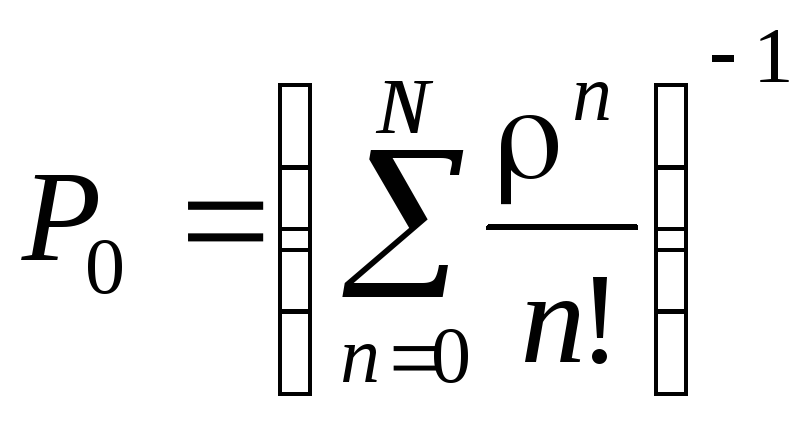 ,
и возвращая теперь
,
и возвращая теперь
![]() в
в![]() имеем
имеем
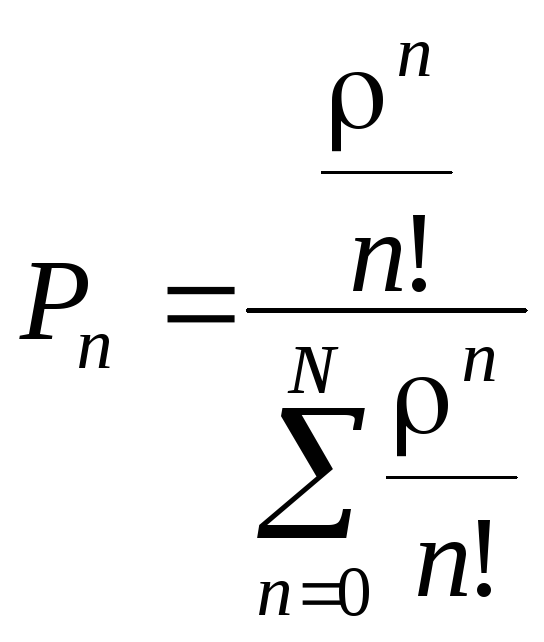 .
(2.36)
.
(2.36)
Блокировка наступает при n=N. Поэтому
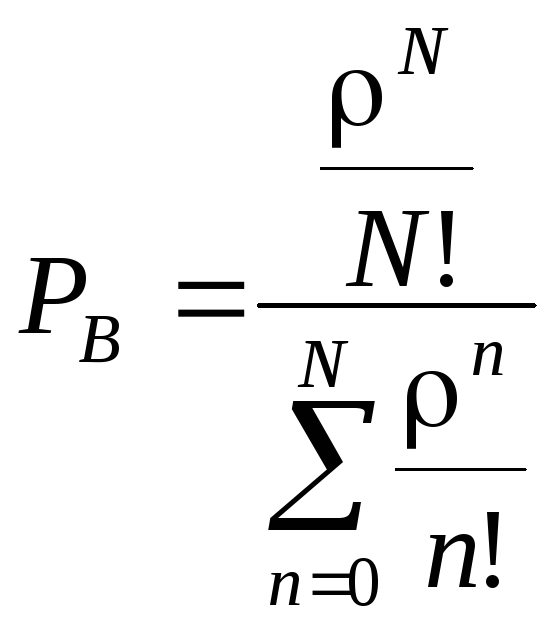 .
(2.37)
.
(2.37)
Формула (2.37) – это распределение Эрланга 1-го рода или В-распределение.
Найдем среднюю занятость системы.
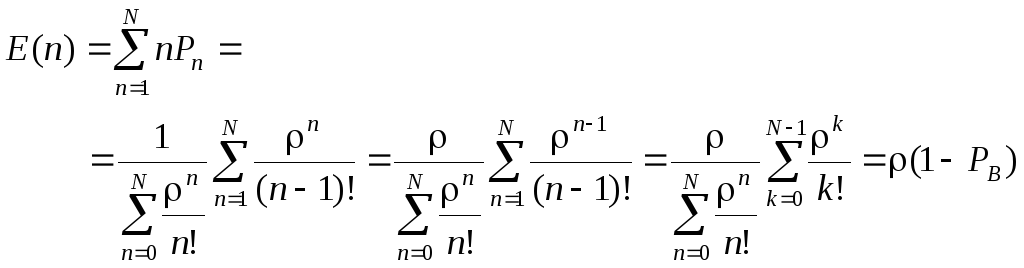 ,
т.е.
,
т.е.
![]() .
(2.38)
.
(2.38)
При
увеличении
вероятность блокировки стремится к
единице
![]() и
и![]() .
.
Производительность , определенная «по входу», равна
![]() ,
(2.39) или –
«по выходу :
,
(2.39) или –
«по выходу :![]() .
.
При
увеличении
производительность стремится к своему
максимальному значению
![]() .
Это происходит тогда, когда
.
Это происходит тогда, когда![]() ,
большинство вызовов блокируется и
,
большинство вызовов блокируется и![]() .
.
Средняя
задержка вызовов, которые приняты
системой равна
![]() ,
т.е.среднему времени обслуживания
(продолжительности занятия). Это
подтверждает формула Литтла
,
т.е.среднему времени обслуживания
(продолжительности занятия). Это
подтверждает формула Литтла
![]() .
(2.40)
.
(2.40)
