2.2. Система обслуживания м/м/1.

Центральным понятием при анализе любой системы является ее состояние, причем под состоянием понимается количество клиентов (пакетов) в системе n, включая клиента, находящегося на обслуживании. Очевидно, n является случайной величиной и задача заключается в определении вероятности любого состояния системы в произвольный момент времени . Если вероятности состояний найдены, то статистические свойства системы (например, среднее время занятия, вероятность блокировки для конечной очереди, средняя пропускная способность и др.) могут быть определены сравнительно просто.

Пусть есть система М/М/1, изображенная на рис. 2.2а.

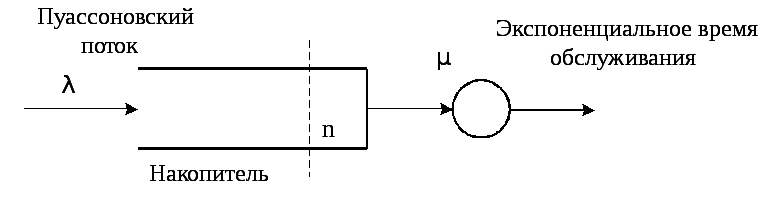
а)

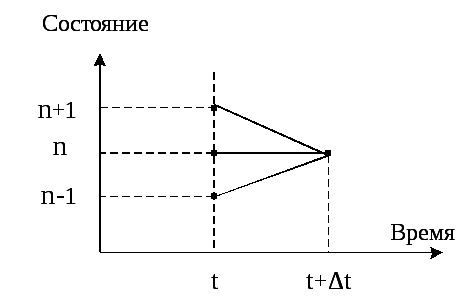
б)

Рис.2.2. Система обслуживания М/М/1 и диаграмма ее состояний.

Интенсивность пуассоновского потока на входе - , а процесс обслуживания (длина пакета или продолжительность соединения) описывается экспоненциальным распределением с параметром μ, которое имеет вид

. (2.1)

Найдём - вероятность того, что в момент в системе будет находитьсяn клиентов. В силу ординарности входного потока есть сумма вероятностей состояний (взаимно исключающих)n-1, n или n+1, в которых система могла быть в момент t (см. диаграмму на рис.2.2б), умноженных на независимые вероятности попадания в состояние n за время Δt.

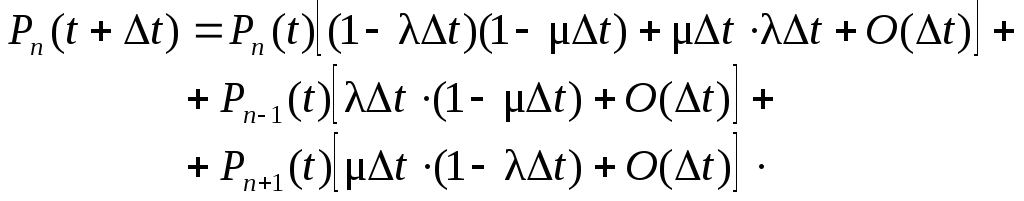(2.2)

При записи (2.2) учтено, что если время обслуживания имеет экспоненциальное распределение, то поток моментов времени завершения обслуживания является пуассоновским потоком. Поэтому вероятность завершения обслуживания за время Δt есть , и, соответственно, вероятность не завершения обслуживания за время Δt равна . Первая строка (2.2), к примеру, характеризует переход , который может произойти либо при одном поступлении и одном уходе – вероятность чего записывается как , либо, если не будет ни поступления, ни ухода с вероятностью .

Преобразуя (отбрасывая члены, пропорциональные ), получим:

. (2.3)

Уравнение (2.3) позволяет исследовать переходный режим системы. Разложим в ряд Тейлора и удержим в ряде два члена

. (2.4)

Подставляя (2.4) в (2.3), получим

. (2.5)

Стационарное значение можно найти из условия. При этом из (2.5) имеем:

. (2.6)

Это уравнение равновесия. Левая часть описывает уходы из состояния n, правая – приходы в состояние n. Графически последовательность состояний и возможные переходы из состояния в состояние отражены на рис.2.3. Состояния отображаются пронумерованными точками, а переходы – стрелками.

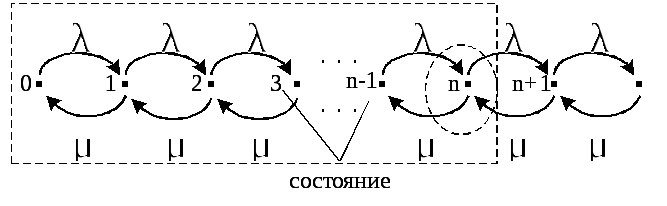
Рис.2.3. Диаграмма состояний системы М/М/1.

Пунктиром на рисунке отмечены две области: овальная область (область 1), охватывающая состояние равновесия n, и прямоугольная область (область 2), охватывающая все состояния от 0 до n . Если для области 1 в состоянии равновесия приравнять исходящий поток (интенсивность уходов из состояния n) входящему потоку (интенсивность прихода в состояние n), то получим уравнение (2.6). Значит, эта диаграмма позволяет не только составить уравнение (2.6), но и решить его. Для этого рассмотрим область 2. Поток, поступающий в эту область: , поток, покидающий его:. Поэтому:

. (2.7)

Уравнение (2.7) выполняется для любого n и удовлетворяет уравнению (2.6), следовательно, может рассматриваться как его решение. Перебирая n, можно записать решение в явном виде: , откуда, далее,и т.д.

В результате получаем , где, аP₀ можно найти из условия нормировки .

Для бесконечной очереди: .

. Здесь использована формула суммы членов геометрической прогрессии, конечный результат в которой достигается при . Поэтому

, (2.8)

и . (2.9)

Итак, равновесие в системе возможно при . Распределение (2.9), характеризующее системуM/M/1, называется геометрическим распределением. Оно представлено на рис.2.4.

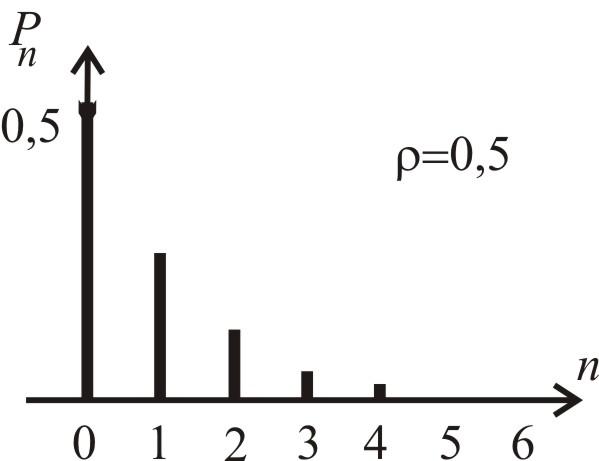
Рис.2.4. Геометрическое распределение.

В силу того, что (т.е. вероятность того, что система пуста,n=0), вероятность того, что система не пуста т.е. равна коэффициенту нагрузки.

Для конечной очереди N уравнение равновесия (2.6) справедливо для всех n, кроме двух граничных точек: n=0 и n=N. Уравнение (2.7) справедливо всегда. Из условия нормировки: , которое после вычисления суммы запишется как, получаемР₀

. (2.10)

Поэтому для конечной очереди из N пакетов в системе M/M/1:

. (2.11)

Вероятность того, что очередь заполнена: . Эта вероятность, по – другому, естьвероятность блокировки, т. е. вероятность того, что пакеты не могут быть приняты системой, т.к. накопитель заполнен. Проиллюстрируем это понятие.

Вероятность блокировки.

Пусть есть произвольная система обслуживания (не обязательно M/M/1), изображенная на рис.2.5.

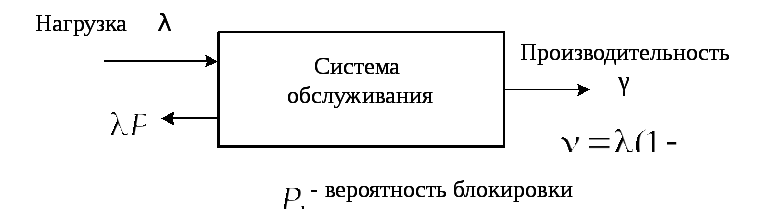
Рис.2.5. К понятию вероятности блокировки.

При наличии блокировки с вероятностью P_B чистая интенсивность поступлений может быть интерпретирована как . Но это должно быть не чем иным, как пропускной способностью (производительностью)или числом клиентов, обслуживаемых в секунду в консервативной системе. Таким образом. Пропускную способность можно определить и другим способом.

Пусть - средняя скорость обслуживания, когда система не пуста. Система пуста с вероятностьP₀. Поэтому фактическая скорость обслуживания . Итак, в системе с конечной очередью:

. (2.12)

Подставим сюда из (2.10)

, где .

Преобразуя, получим: , что совпадает сдля системыM/M/1 с конечной очередью.

Если и, то,и, что совпадает с выражением (2.9) для системыM/M/1 с бесконечной очередью, то есть это есть вероятность того, что система находится в состоянии n=N. Таким образом, при усечение бесконечной очереди в точкеn=N не повлияет на статистику очереди.

Пример: . В системеM/M/1 требуется реализовать . Из выражениянаходимN=9. Если , то N=19.

Исследуем выражение (2.11). Для существования стационарных вероятностей здесь не требуется . Эти вероятности существуют из-за конечности очереди для любого. При увеличении, из-за увеличенияочередь переполняется всё более часто и приочередь находится в состоянииn=N с вероятностью 1. Характер зависимости представлен на рис.2.6.

При для всех, а, т. е.. Областьназывается областью скученности, здесь наиболее вероятны состояния очереди с наивысшими номерами. При(с использованием правила Лопиталя) можно получить.

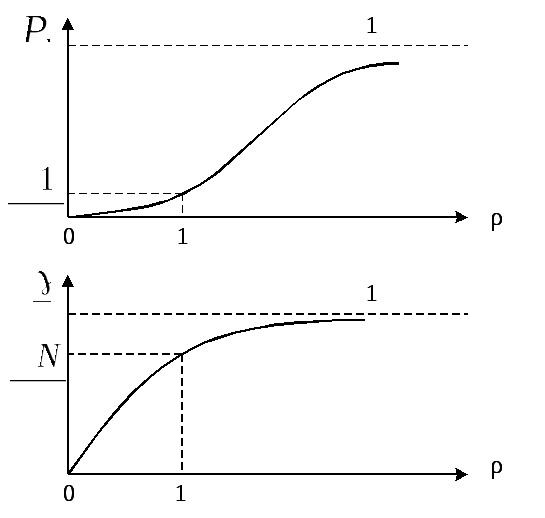
Рис.2.6. Характеристики системы M/M/1 при конечной очереди.

Из (2.12) можно получить . Данное выражение представляет собой нормированную производительность системыM/M/1 с конечной очередью. Зависимость от также представлена на рис.2.6. При получаем, и при.

Сравнение поведения системы M/M/1 при конечной и бесконечной очереди позволяет сделать вывод, что в области целесообразно исследовать только бесконечный накопитель. Как было указано выше, на основе известного распределения вероятностей состоянийможно рассчитывать различные характеристики системы.

Найдем среднее число клиентов в системе E(n).

С учетом , получаем

. (2.13)

Результат (2.13) можно получить непосредственно, используя формулу [ 8 ]

, где для нашего случая a=0 и r=1.

График зависимости среднего числа клиентов от  приведен на рис.2.7.

Из (2.13) следует, что при малой нагрузке число клиентов в очереди мало, с увеличением нагрузки () число клиентов в очереди тоже увеличивается (за счётв знаменателе). Сравнивая два последних рисунка можно сказать, что при росте нагрузки системы растёт и её производительность, однако, всё большее количество клиентов блокируется и растёт среднее число клиентов в очереди.

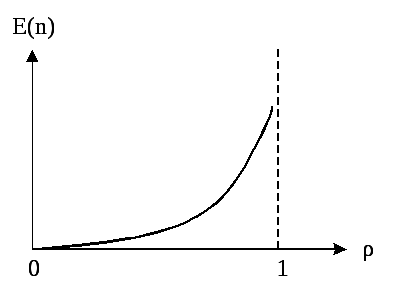
Рис.2.7. Зависимость E(n) от  для системы M/M/1.

2.3. Формула Литтла.

В предыдущем параграфе было рассчитано среднее число клиентов в системе М/М/1. С величиной Е(n) тесно связана временная характеристика системы, которая называется время задержки Т, и которая включает в себя время ожидания в очереди W и время обслуживания (см.рис.2.8). В силу того, что  в однолинейной системе представляет собой среднюю интенсивность обслуживания можно не вводить специального обозначения для среднего времени обслуживания, а просто писать .

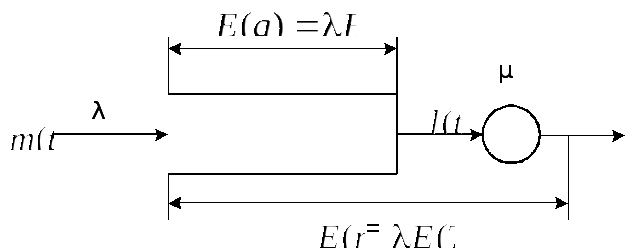
Рис. 2.8. Время задержки в однолинейной системе.

Поэтому . (2.14)

Очевидно, должна существовать связь среднего времени задержки клиента в системе Е(Т) со средним числом клиентов E(n) в установившемся режиме. Установим эту связь.

Обозначим через m(t) число поступлений в систему к мо-менту времени t на интервале (0, t). Число уходов из накопителя на обслуживание на этом же интервале – l(t). Никаких предположений относительно процессов поступлений и уходов не делается, т.е. полученный результат будет справедлив для любых типов однолинейных систем. В соответствие с введенными обозначениями для числа s(t) ожидающих клиентов в системе к моменту времени t можно записать

.

На рис.2.9 m(t) изображена сплошной линией, а l(t) – пунктиром. Там же отмечены моменты поступления клиентов в систему и моменты ухода на обслуживание,. Пусть дисциплина обслуживания – в порядке поступления, тогдаСоответственно- время ожидания j-го клиента.

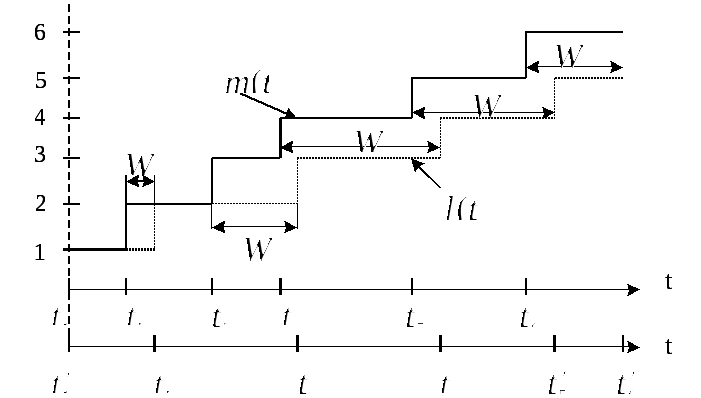
Рис.2.9. К выводу формулы Литтла.

Рассмотрим интервал . Число поступлений на этом интервале, а средняя интенсивность поступлений

. (2.15)

Найдем . Этот интеграл определяется как площадь под разностью. Из рисунка следует, что эта площадь состоит из прямоугольников единичной высоты и длины.

. (2.16)

Пусть - среднее время ожидания в промежутке. Тогда

. (2.17)

Среднее число клиентов в системе

. (2.18)

Из (2.16), (2.17) и (2.18) имеем

или .

Это и есть формула Литтла. При ,,и для установившегося режима можно записать окончательно

. (2.19)

Формула Литтла справедлива при любой дисциплине обслуживания. Это можно показать из соотношения

,

которое следует интерпретировать так, что сумма слева зависит только от суммы времен ухода, а не от разности .

Вернемся к системе M/M/1.

Формулу Литтла перепишем в привычных обозначениях: . Теперь

. (2.20)

При - здесь задержка определяется только обслуживанием. Последний результат представлен графически на рис.2.10, где по оси ординат отложена нормированная задержка, т.е. нормировка осуществляется делением на среднее время обслуживания.

Рис.2.10. Нормированная средняя задержка.

Со средним временем задержки E(T) можно связать ещё понятия (см.рис.2.8)

E(W) – среднее время ожидания в очереди,

E(q) – среднее число клиентов, ожидающих в очереди.

Кроме очевидного равенства (2.14), на основе формулы Литтла, которая применима не только ко всей системе, но и к ее части, можно записать

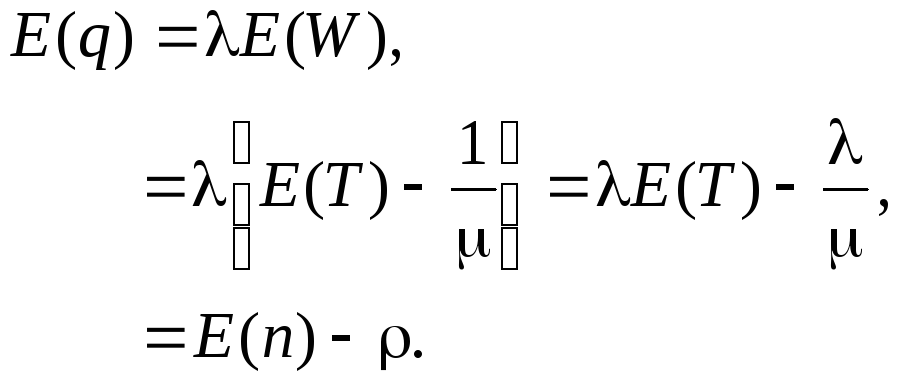(2.21)

В (2.21) понимается как среднее число клиентов на обслуживании. Оно меньше 1, т. к. на обслуживание либо есть клиент, либо нет. Этот результат подтверждается уже известным для системы М/М/1 фактом:- это вероятность того, что ни один клиент не обслуживается,- это вероятность того, что на обслуживание находится один клиент.

Эти рассуждения справедливы для любой однолинейной системы.