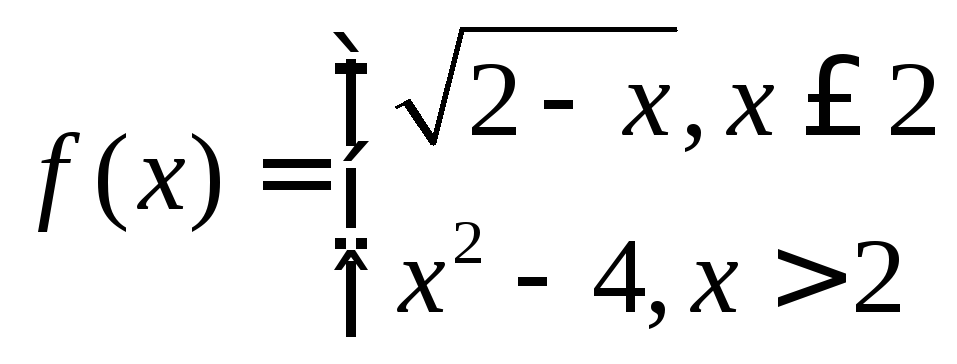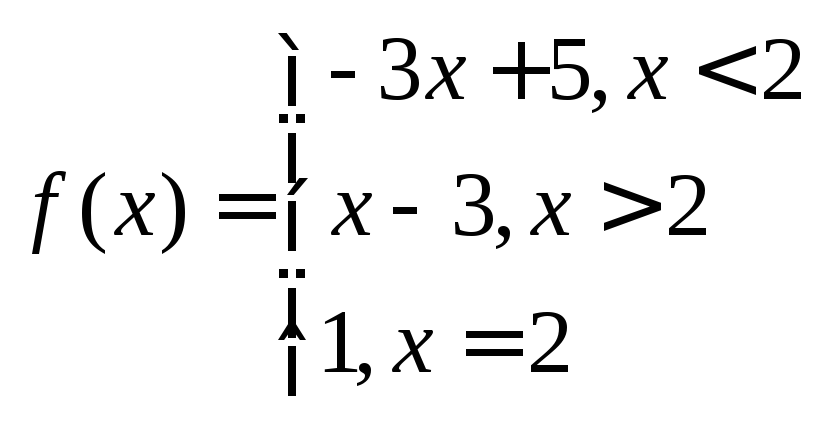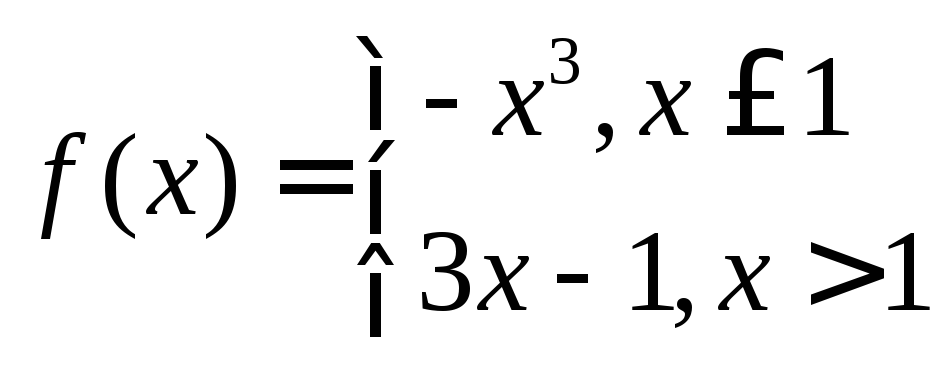- •Пределы и непрерывность
- •Глава 1. Пределы числовых последовательностей и функций.
- •§ 1. Числовая последовательность и ее предел
- •§ 2. Предел функции в бесконечности и в точке
- •§ 3. Основные теоремы о пределах. Вычисление пределов функций
- •§ 4. Бесконечно малые величины и их применение к отысканию пределов
- •§5. Замечательные пределы
- •Глава 2. Непрерывность функции. Точки разрыва. Их классификация
- •§1. Непрерывные функции. Односторонние пределы
- •§2. Точки разрыва и их классификация
- •Контрольная работа
§1. Непрерывные функции. Односторонние пределы
Определение.
Функция
![]() называетсянепрерывной
в точке
называетсянепрерывной
в точке
![]() ,
если она удовлетворяет следующим трем
условиям:
,
если она удовлетворяет следующим трем
условиям:
Определена в точке
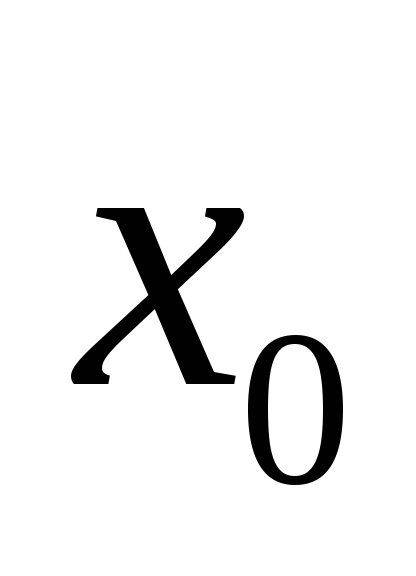 (т.е. существует
(т.е. существует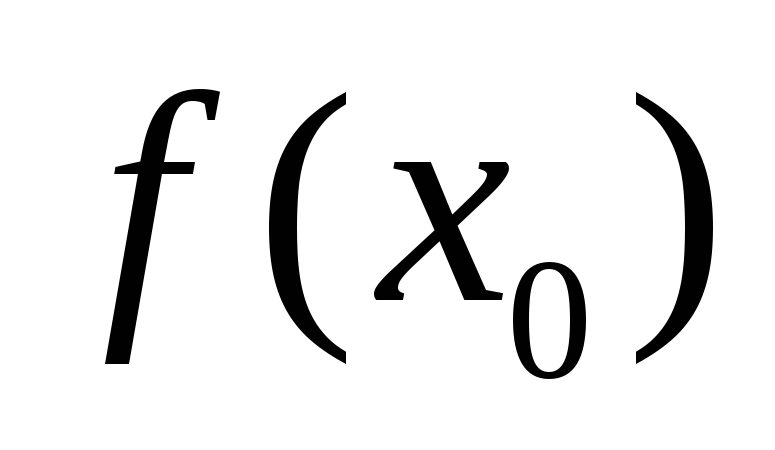 );
);Имеет конечный предел функции при
 ;
;Этот предел равен значению функции в точке
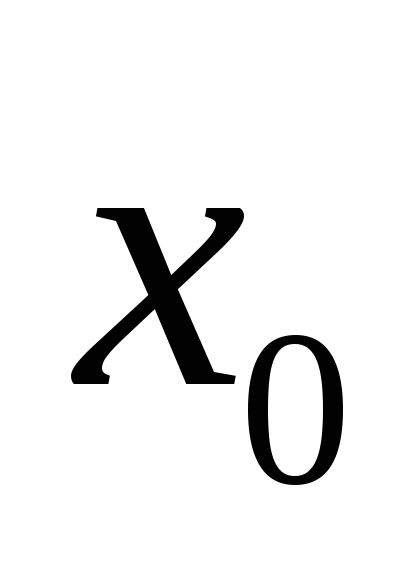 ,
т.е.
,
т.е.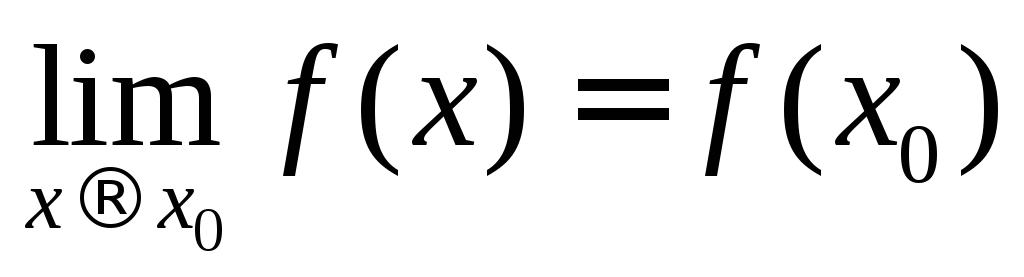 .
.
Если
хотя бы одно из условий не выполняется,
то функция называется разрывной
в точке
![]() а сама точка
а сама точка![]() называетсяточкой
разрыва
функции.
называетсяточкой
разрыва
функции.
Односторонние пределы.
Односторонние
пределы бывают правосторонними,
когда
![]() стремится
к своему предельному значению, оставаясь
больше него, илевосторонними,
когда
стремится
к своему предельному значению, оставаясь
больше него, илевосторонними,
когда
![]() стремится
к своему предельному значению, оставаясь
меньше него. Правосторонний предел
обозначается
стремится
к своему предельному значению, оставаясь
меньше него. Правосторонний предел
обозначается![]() или
или![]() ,
а левосторонний
,
а левосторонний![]() или
или![]() .
.
![]() Пример
1 Найти
односторонние пределы
Пример
1 Найти
односторонние пределы
a)
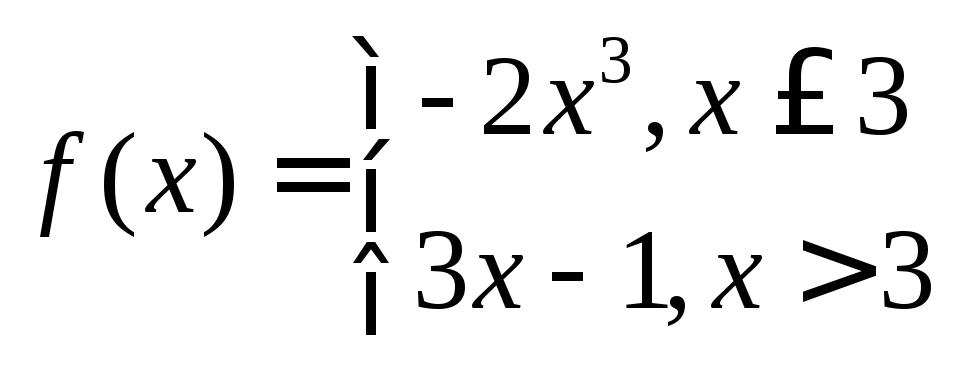 в точке
в точке![]() .
.
![]() Решение:
Решение:
![]()
![]()
b)
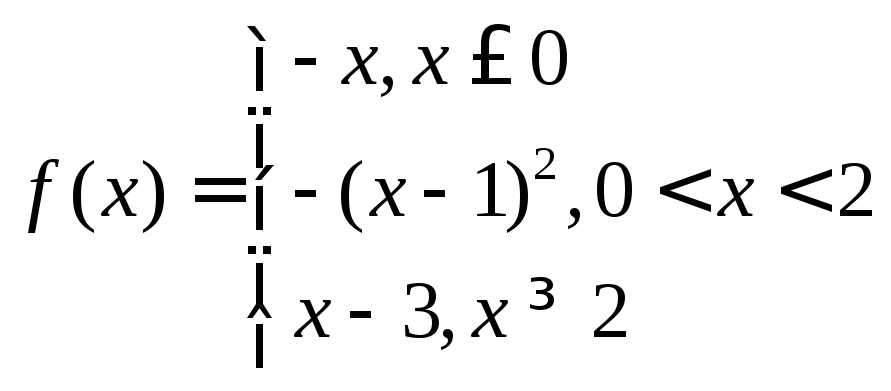 в точках
в точках
![]() ,
,![]() .
.
![]() Решение:
Решение:
![]()
![]()
![]()
![]()
c)
![]() в точке
в точке
![]()
![]() Решение:
Решение:
![]()
![]()
d)
![]() в точке
в точке
![]() .
.
![]() Решение:
Решение:
![]()
![]()
Задачи для выполнения на практических занятиях:
Найти односторонние пределы функций:
1)
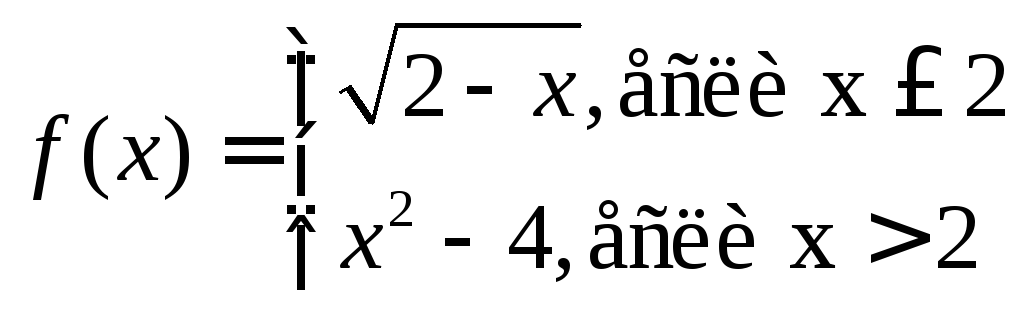 в точке
в точке![]()
2)
![]() в точке
в точке![]()
3)
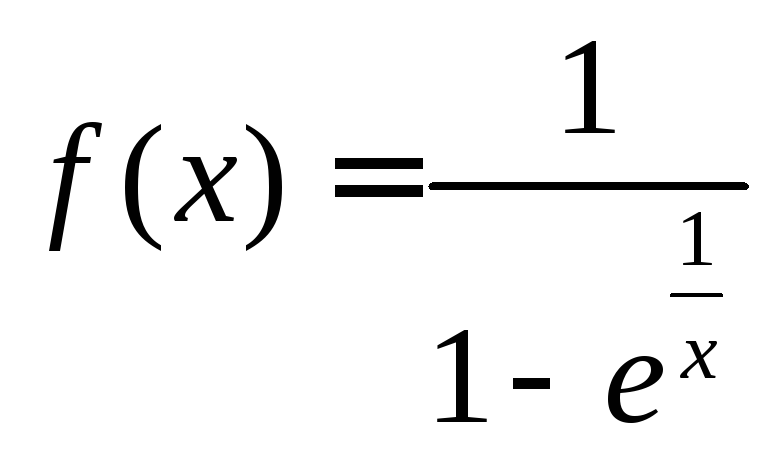 в точке
в точке![]()
4)![]() в точке
в точке![]()
5)![]() в точке
в точке![]()
6)![]() в точке
в точке![]()
Задачи для самостоятельного решения:
1)
![]() в точке
в точке![]()
2)![]() в точке
в точке![]()
3)
![]() в точке
в точке![]()
4)
![]() в точке
в точке![]()
5)
![]() в точке
в точке![]()
§2. Точки разрыва и их классификация
Определение.
Точка
![]() называетсяточкой
разрыва
функции
называетсяточкой
разрыва
функции
![]() ,
если эта функции в данной точке не
является непрерывной.
,
если эта функции в данной точке не
является непрерывной.
1.
Если
![]() ,
то функция
,
то функция![]() называется непрерывной в точке
называется непрерывной в точке![]() .
.
2.
Если
![]() ,
то точка
,
то точка![]() называется точкой разрыва первого рода
(разрыв устранимый).
называется точкой разрыва первого рода
(разрыв устранимый).
3.
Если
![]() ,
то точка
,
то точка![]() называется
точкой разрыва первого рода (разрыв
неустранимый).
называется
точкой разрыва первого рода (разрыв
неустранимый).
4.
Если
![]() и
(или)
и
(или)![]() ,
то точка
,
то точка![]() называется точкой разрыва второго рода.
называется точкой разрыва второго рода.
Разрыв второго рода не делится на устранимый и неустранимый.
![]() Пример
2
Исследовать
на непрерывность и найти точки разрыва,
если таковые существуют.
Пример
2
Исследовать
на непрерывность и найти точки разрыва,
если таковые существуют.
![]() Решение:
Решение:
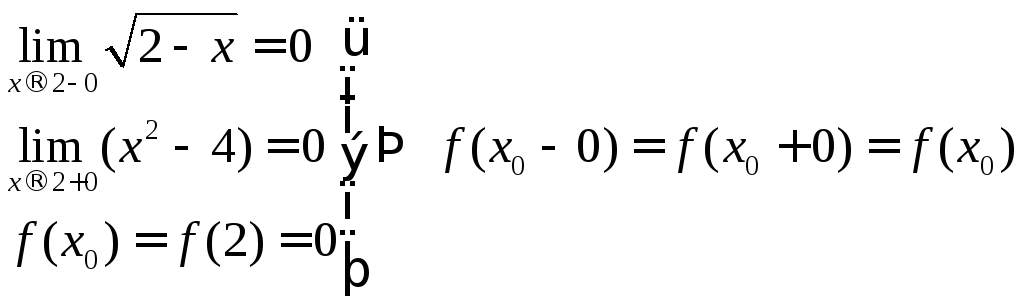 ,
т.е.
,
т.е.
![]() -
непрерывная функция.
-
непрерывная функция.
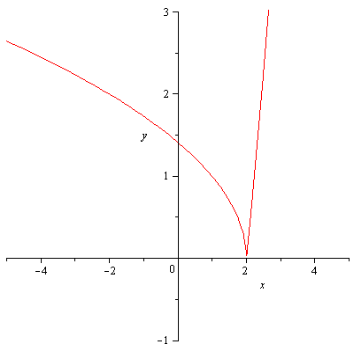
![]() Решение:
Решение:
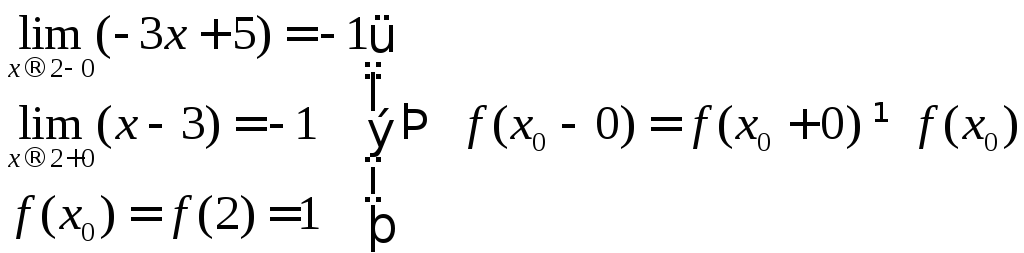 ,
т.е.
,
т.е.
![]() -
точка разрыва первого рода, причем
разрыв устранимый.
-
точка разрыва первого рода, причем
разрыв устранимый.
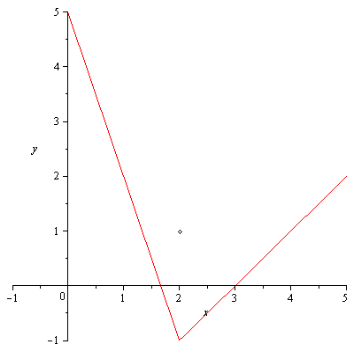
![]() Решение:
Решение:
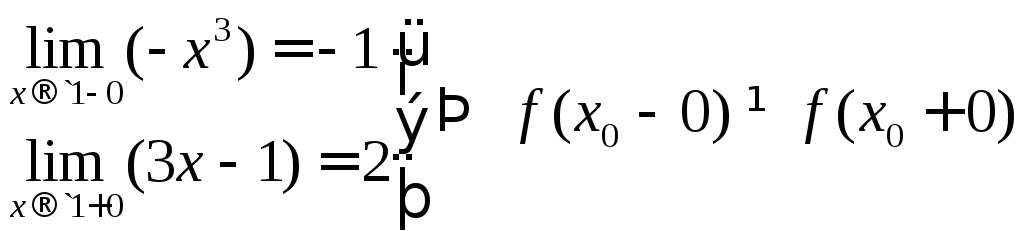 ,
т.е.
,
т.е.
![]() -
точка разрыва первого рода.
-
точка разрыва первого рода.
В точке
![]() функция
терпит скачок, поэтому разрыв неустранимый.
функция
терпит скачок, поэтому разрыв неустранимый.
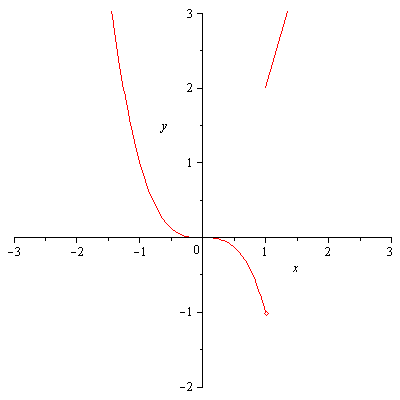
![]() Решение:
Решение:
![]() ,
т.е.
,
т.е.
![]() -
точка разрыва второго рода.
-
точка разрыва второго рода.
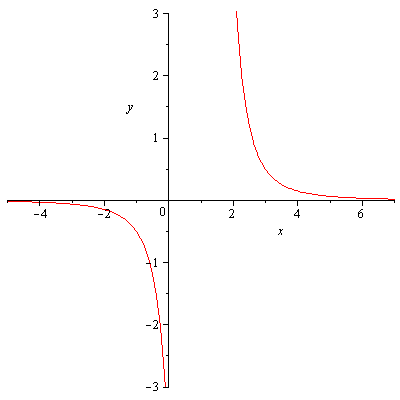
![]() Решение:
Решение:
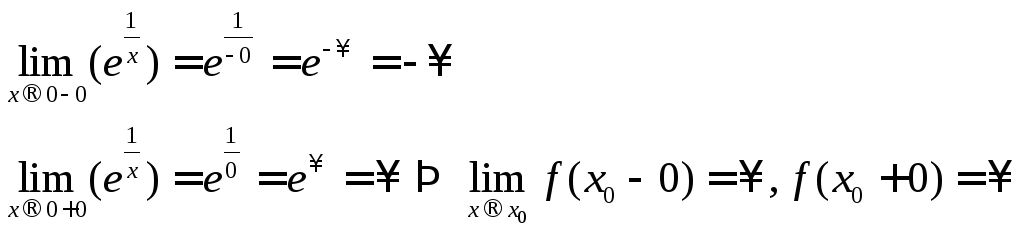
т.е.
![]() -
точка разрыва второго рода.
-
точка разрыва второго рода.
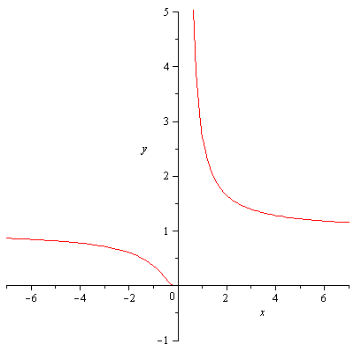
![]() Решение:
Решение:
![]() ,
т.е.
,
т.е.
![]() -
точка разрыва второго рода.
-
точка разрыва второго рода.

Задачи для выполнения на практических занятиях:
Исследовать на непрерывность и найти точки разрыва функций
1)![]()
2)
![]()
3)
![]()
4)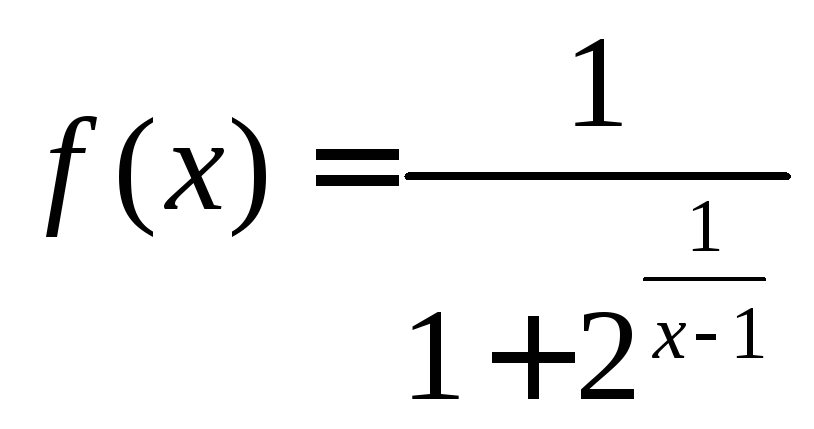
5)
![]()
6)

7)
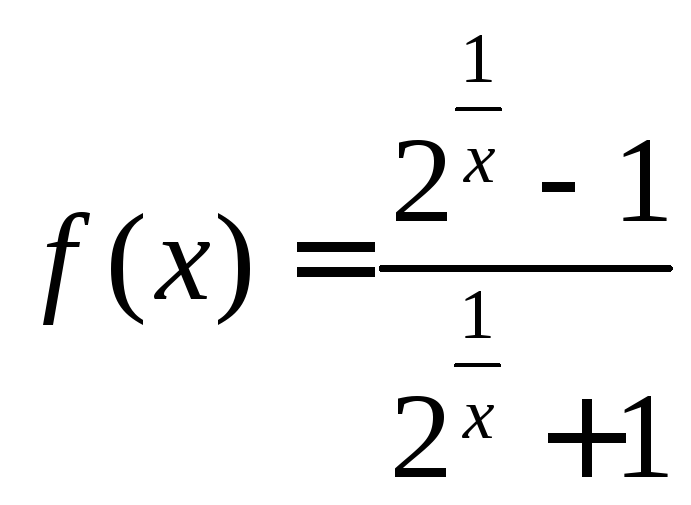
Задачи для самостоятельного решения:
Исследовать на непрерывность и найти точки разрыва функций
1)

2)
![]()
3)
![]()
4)
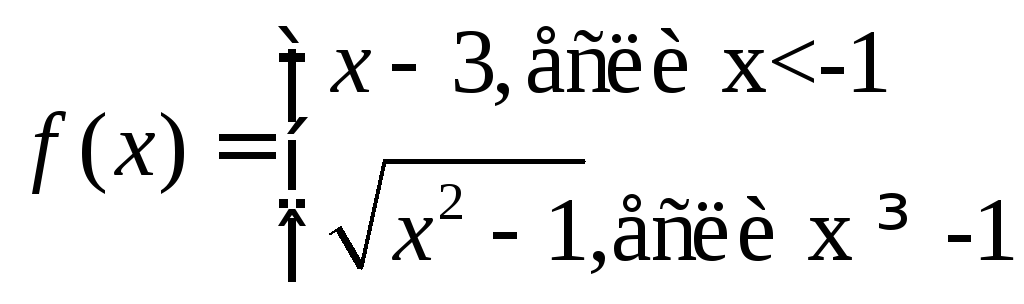
5)
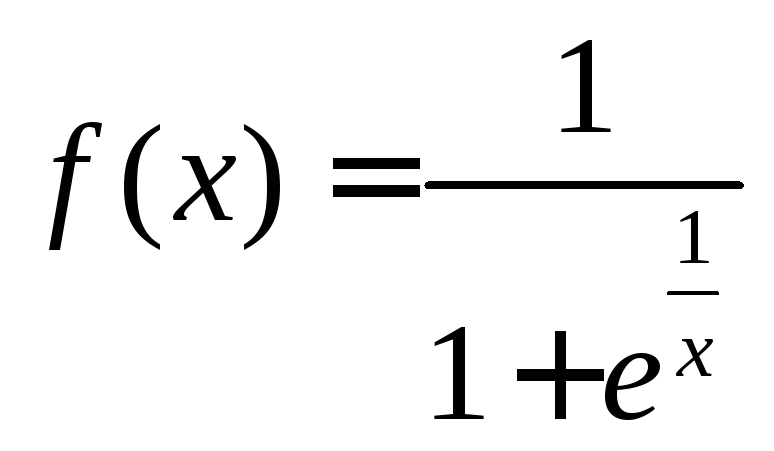
6)
![]()
Контрольная работа
Вычислить пределы:
Исследовать на разрыв функцию
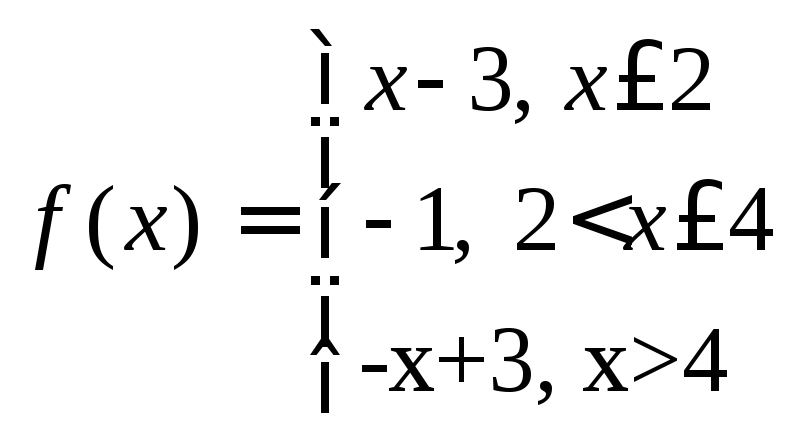
Ответы:
Глава 1.
§ 1
Задания для выполнения на практических занятиях:
0 2)
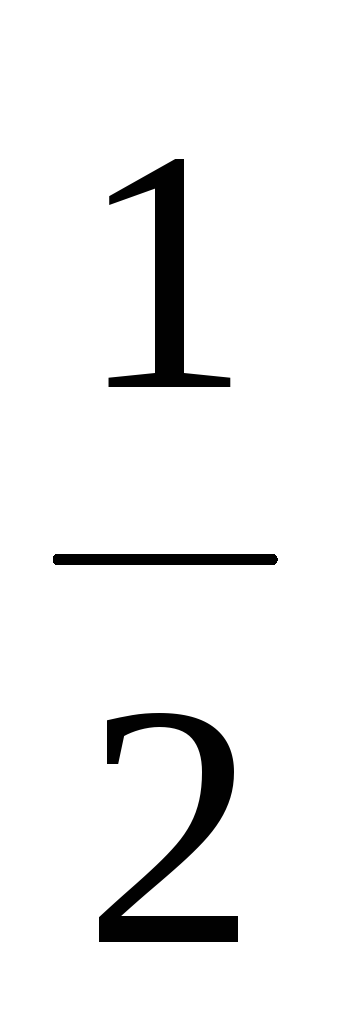 3) 1
4) 1
5) 0,01
6) 5
7) 0
8) 0
9) 0
10)
0
3) 1
4) 1
5) 0,01
6) 5
7) 0
8) 0
9) 0
10)
0
Задачи для самостоятельной работы:
 2)
2)
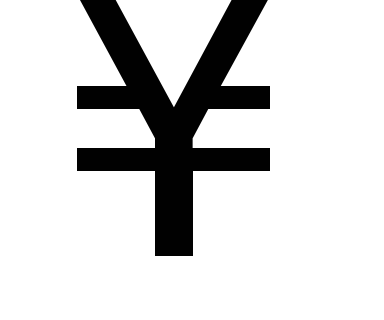 3) 0
4)
3) 0
4)
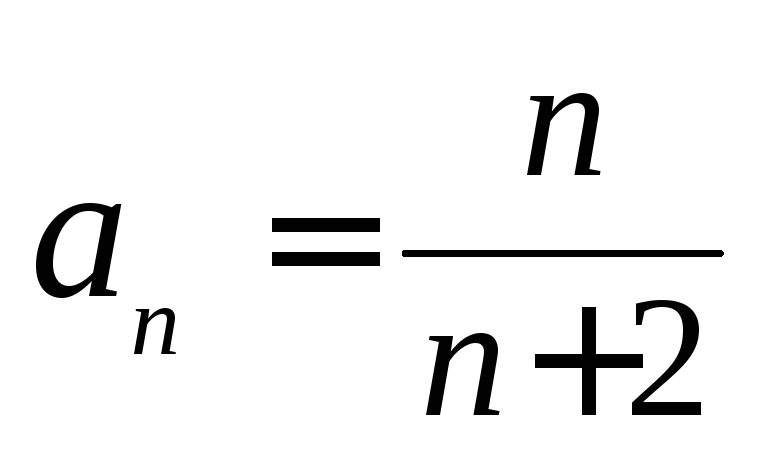 5)
5)
 6)
6)

§ 3
Задания для выполнения на практических занятиях:
1) 0
2) 0
3) -2
4)
![]() 5)
5)
![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]() 9)
9)
![]() 10) 0
10) 0
Задачи для самостоятельной работы:
1)
![]() 2) 0
3) 0
4)
2) 0
3) 0
4)
![]() 5) 1
6)
5) 1
6)
![]()
§ 4
Задания для выполнения на практических занятиях:
1) 0
2)
![]() 3)
3)
![]() 4)
4)
![]() 5) 1
6)
5) 1
6)
![]() 7)
7)
![]() 8)
8)
![]() 9)
9)
![]() 10)
10)
![]()
Задачи для самостоятельной работы:
1) 2
2)
![]() 3) 1
4)
3) 1
4)
![]() 5)
5)
![]() 6)
6)
![]()
§ 5
Задания для выполнения на практических занятиях:
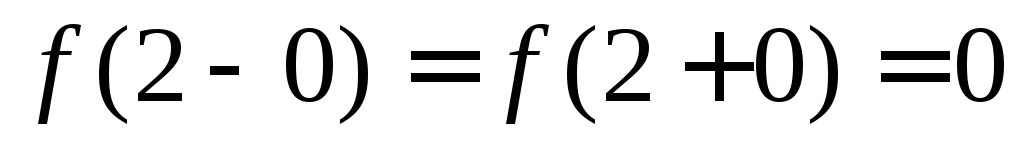 2)
2)

3)![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
Задачи для самостоятельной работы:
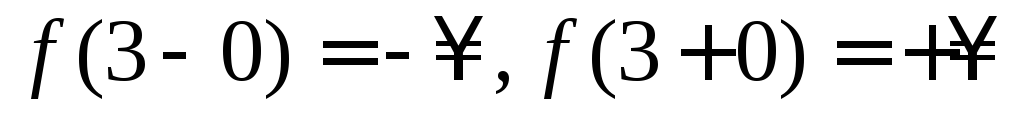 2)
2)
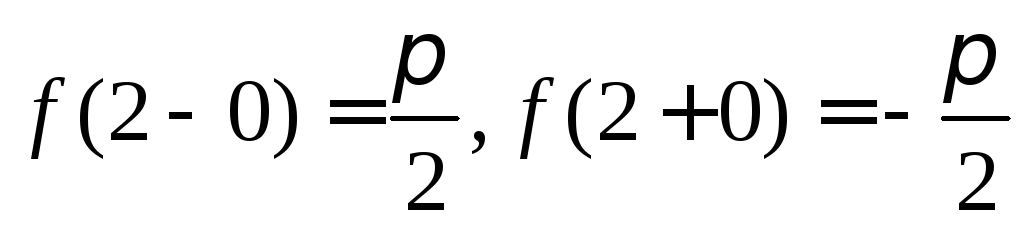
3)
![]() 4)
4)
![]()
5)
![]()
Глава 2.
§ 1
Задания для выполнения на практических занятиях:
1)![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]() 5)
5)
![]() 6) 1
7)
6) 1
7)
![]() 8)
8)
![]() 9)
9)
![]() 10)
10)
![]() 11)
11)
![]() 12)
12)
![]()
Задачи для самостоятельной работы:
1)
![]() 2)
2)
![]() 3) 0
4)
3) 0
4)
![]() 5)
5)
![]() 6)
6)
![]()
§ 2
Задания для выполнения на практических занятиях:
1) в
точке
![]() функция
непрерывна
функция
непрерывна
2) в
точках
![]() функция имеет разрыв второго рода
функция имеет разрыв второго рода
3) в
точке
![]() функция
имеет разрыв первого рода
функция
имеет разрыв первого рода
4) в
точке
![]() функция
имеет разрыв (неустранимый) первого
рода
функция
имеет разрыв (неустранимый) первого
рода
5) в
точке
![]() функция имеет разрыв второго рода
функция имеет разрыв второго рода
6) в
точке
![]() функция
имеет разрыв (неустранимый) первого
рода
функция
имеет разрыв (неустранимый) первого
рода
7) в
точке
![]() функция
имеет разрыв первого рода
функция
имеет разрыв первого рода
Задачи для самостоятельной работы:
1)
в точке
![]() функция
имеет разрыв первого рода
функция
имеет разрыв первого рода
2) в
точке
![]() функция
имеет разрыв первого рода
функция
имеет разрыв первого рода
3) в
точке
![]() функция имеет разрыв второго рода
функция имеет разрыв второго рода
4) в
точке
![]() функция
имеет разрыв первого рода
функция
имеет разрыв первого рода
5) в
точке
![]() функция
имеет разрыв первого рода
функция
имеет разрыв первого рода
6) в
точках
![]() функция имеет разрыв второго рода
функция имеет разрыв второго рода
Литература
Щипачев В.С. Высшая математика. Учебник для вузов. М.: «Высшая школа», 2001-479с.
Высшая математика для экономистов: Учебник для втузов /Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман; под редакцией профессора Н. Ш. Кремера – 2-ое издание, перераб. и доп. – М: Банки и Биржи, ЮНИТИ, 1998 - 471с.
Сборник задач по курсу высшей математики. Под редакцией Г. И. Кручковича. Изд. 3, перераб. Учебное пособие для втузов. М., «Высшая школа», 1973. 576с. С илл.
Гусак А.А. Пособие к решению задач по высшей математике. Изд. 3-е, стереотип. Мн.. Изд. БГУ, 1973. 532 стр. с илл.
П.Е. Данко, А.Г. Попов. Высшая математика в упражнениях и задачах. Ч 1. Учебное пособие для втузов. М, «Высшая школа», 1974-464с.
Лунгу К.Н. Сборник задач по высшей математике. М: Айрис-пресс, 2008-576с.
Баранова Е.С., Васильева Н.В., Федотов В.П. Практическое пособие по высшей математике. С-Петербург: «Пиллер», 2009-320с.