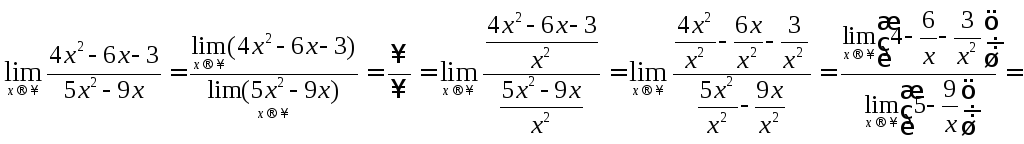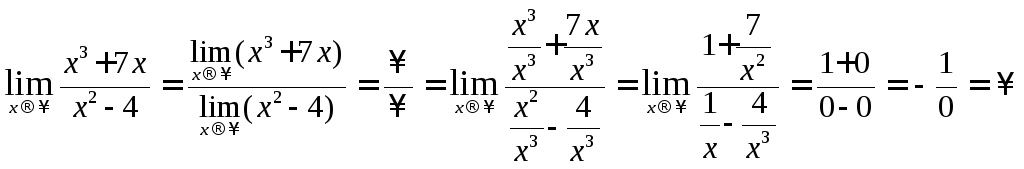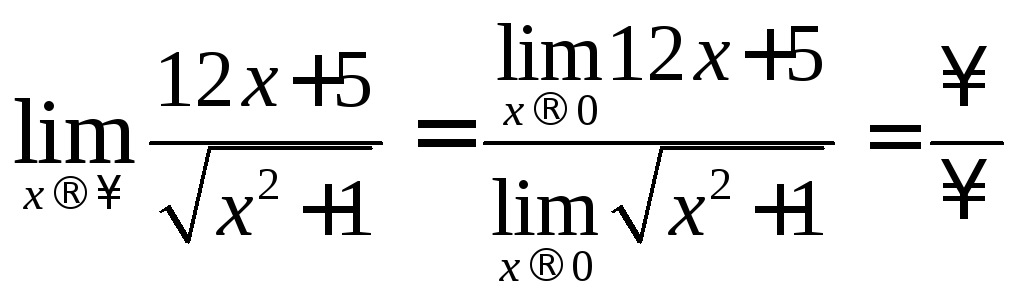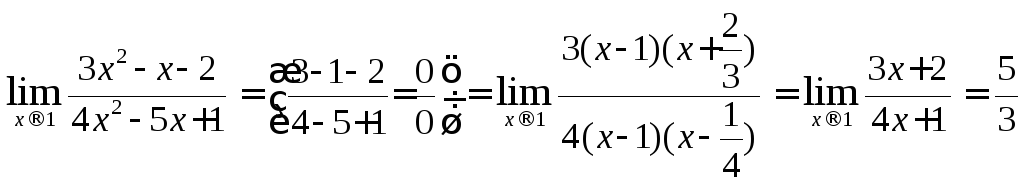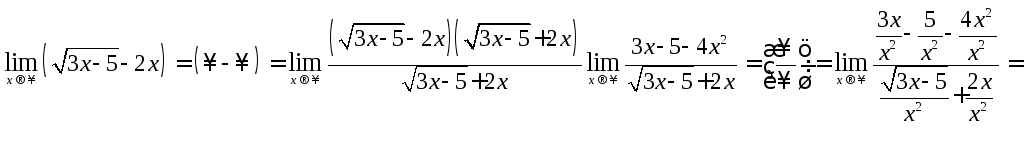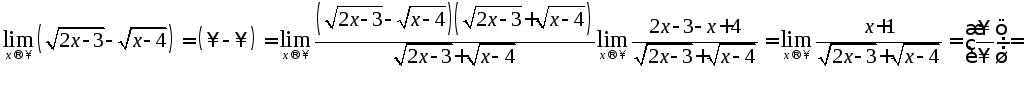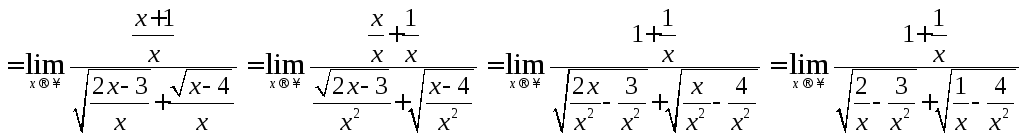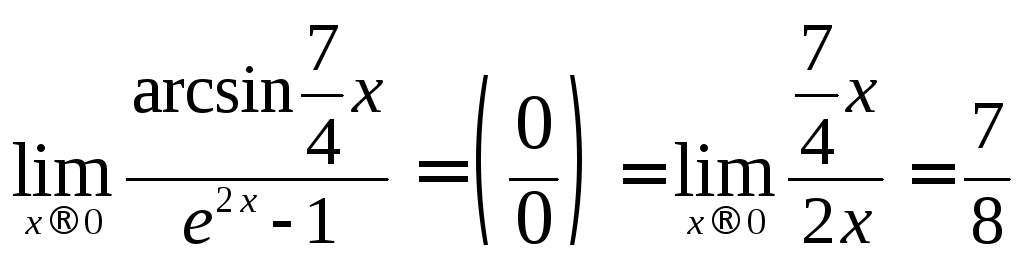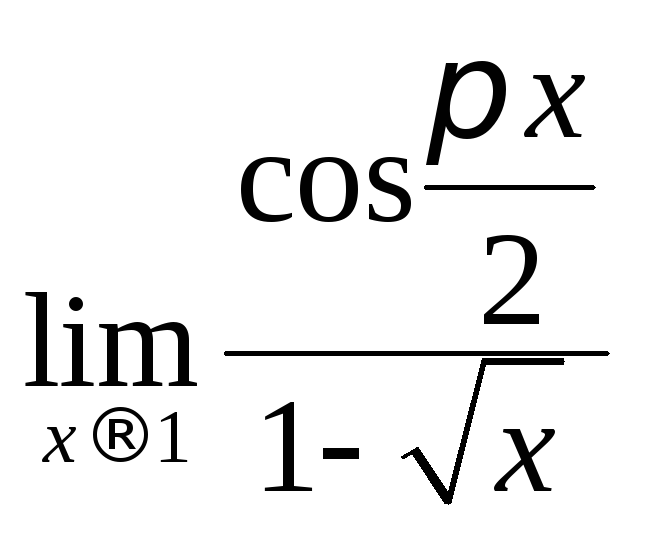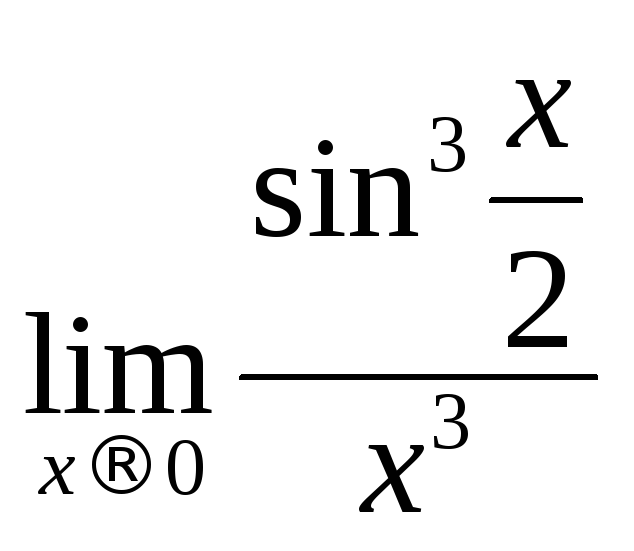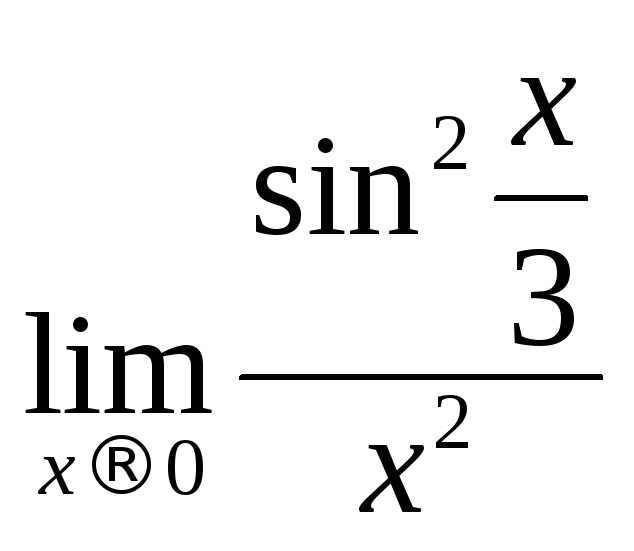- •Пределы и непрерывность
- •Глава 1. Пределы числовых последовательностей и функций.
- •§ 1. Числовая последовательность и ее предел
- •§ 2. Предел функции в бесконечности и в точке
- •§ 3. Основные теоремы о пределах. Вычисление пределов функций
- •§ 4. Бесконечно малые величины и их применение к отысканию пределов
- •§5. Замечательные пределы
- •Глава 2. Непрерывность функции. Точки разрыва. Их классификация
- •§1. Непрерывные функции. Односторонние пределы
- •§2. Точки разрыва и их классификация
- •Контрольная работа
§ 3. Основные теоремы о пределах. Вычисление пределов функций
При вычислении пределов функций пользуются следующими основными теоремами:
Если предел функции существует, то он единственный
 ,
где
,
где
 - постоянная
- постоянная
Если
![]() и
и![]() существуют, то :
существуют, то :
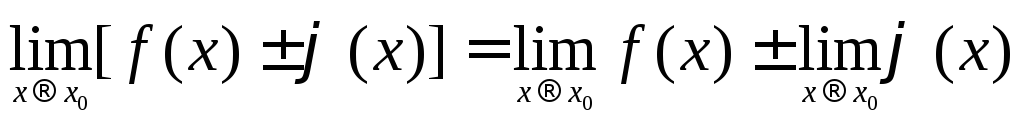
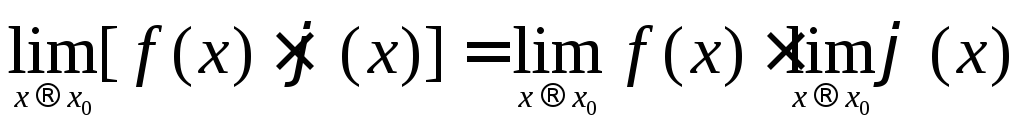 и
и
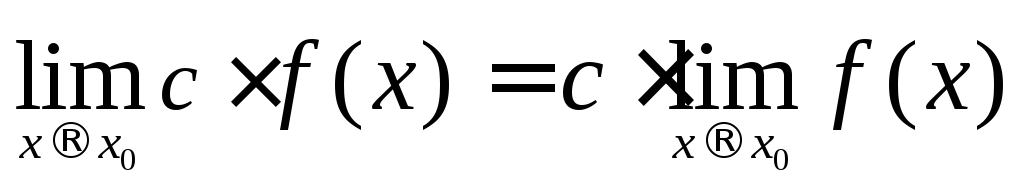 ,
где
,
где - постоянная
- постоянная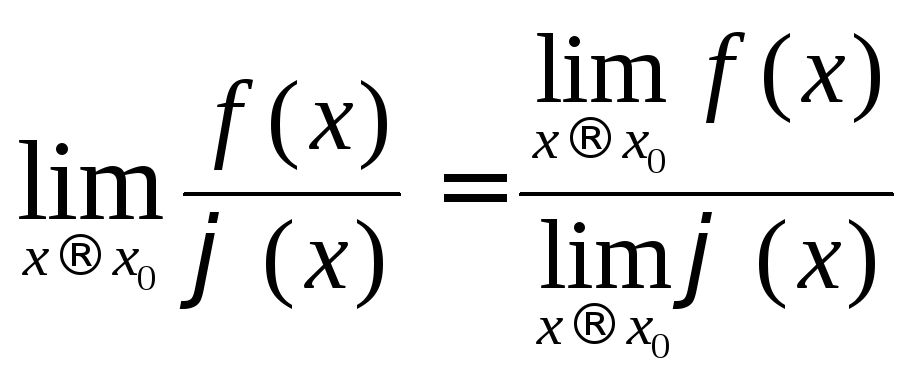 ,
если
,
если
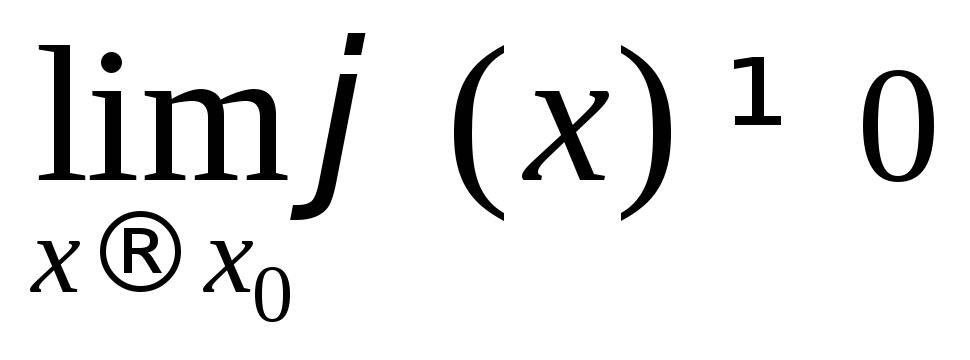
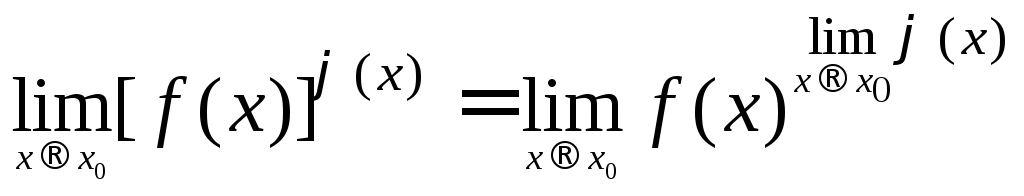
Для всех основных элементарных функций:
Кроме того
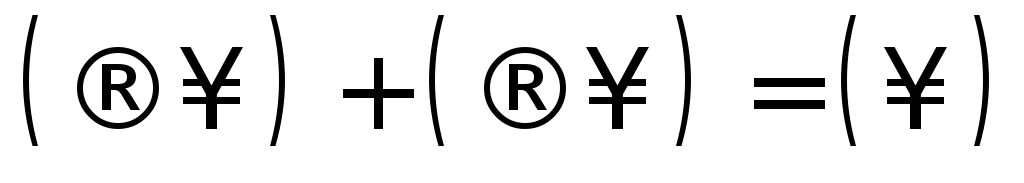
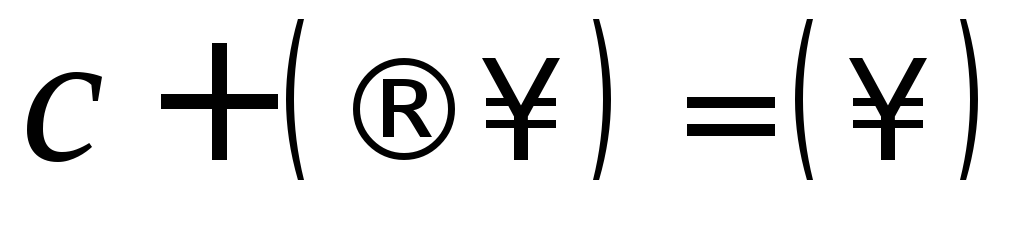
 -неопределенность
-неопределенность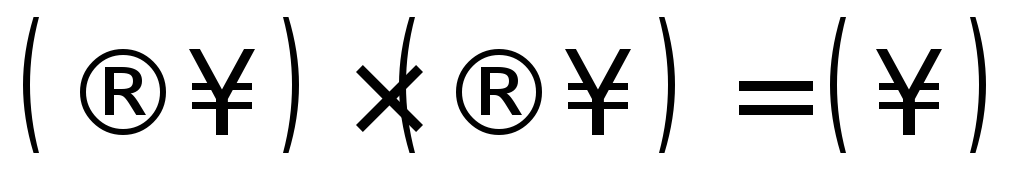
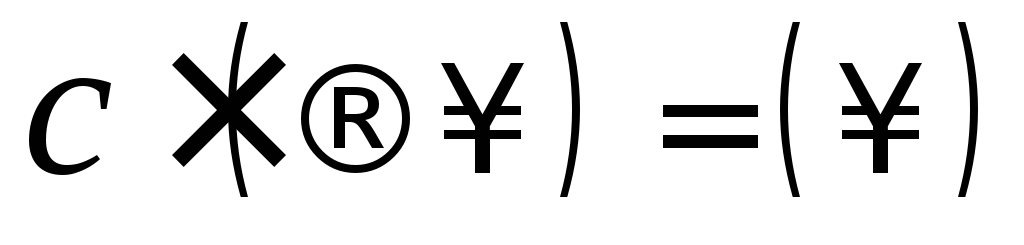
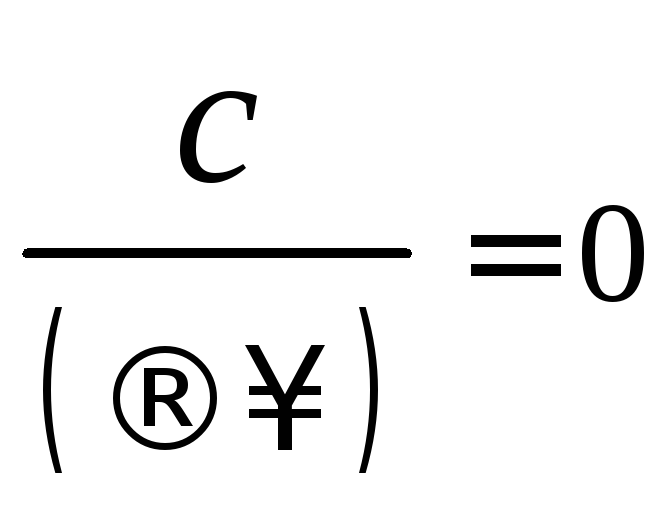

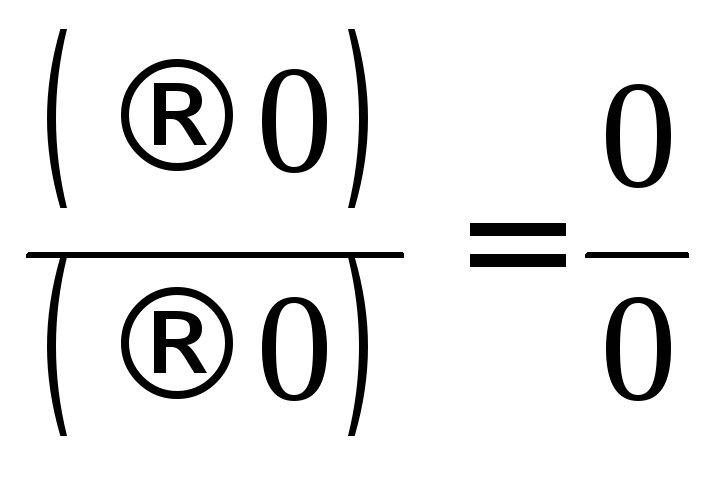 -
неопределенность
-
неопределенность
Вычисление пределов функций
Нахождение предела
в точке
![]() обычно сводится к подстановке в данную
функцию предельного значения аргумента.
Это иногда приводит к неопределенным
выражениям вида
обычно сводится к подстановке в данную
функцию предельного значения аргумента.
Это иногда приводит к неопределенным
выражениям вида![]() .
Нахождение предела функции в этих
случаях называется раскрытием
неопределенности. Для раскрытия
неопределенности приходится проводить
различные преобразования данной функции.
.
Нахождение предела функции в этих
случаях называется раскрытием
неопределенности. Для раскрытия
неопределенности приходится проводить
различные преобразования данной функции.
Замечание 6 Чтобы
раскрыть неопределенность вида
![]() ,
заданную отношением двух многочленов
надо числитель и знаменатель разделить
на самую высокую входящую в них степень
х, а затем перейти к пределу.
,
заданную отношением двух многочленов
надо числитель и знаменатель разделить
на самую высокую входящую в них степень
х, а затем перейти к пределу.
![]() Пример 7
Вычислить
пределы:
Пример 7
Вычислить
пределы:
![]()
Чтобы раскрыть
неопределенность
![]() необходимо разделить числитель и
знаменатель на х подведем х под знак
корня
необходимо разделить числитель и
знаменатель на х подведем х под знак
корня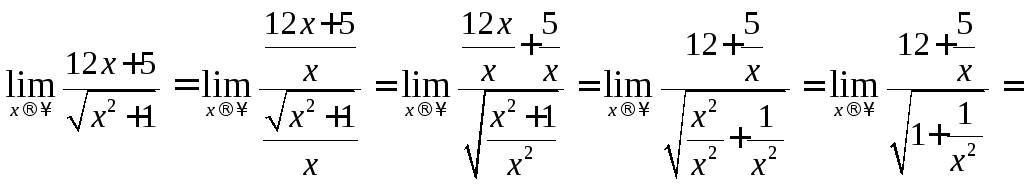
![]() =
=![]()
Здесь
![]() и
и![]()
Замечание 7 Если
дана рациональная функция
![]() ,
то
,
то
Замечание 8: Чтобы
раскрыть неопределенность вида
![]() ,
надо в числителе и в знаменателе выделить
критический множитель (т.е. множитель
равный нулю при предельном значении х)
и сократить на него.
,
надо в числителе и в знаменателе выделить
критический множитель (т.е. множитель
равный нулю при предельном значении х)
и сократить на него.
![]() Пример 8
Пример 8
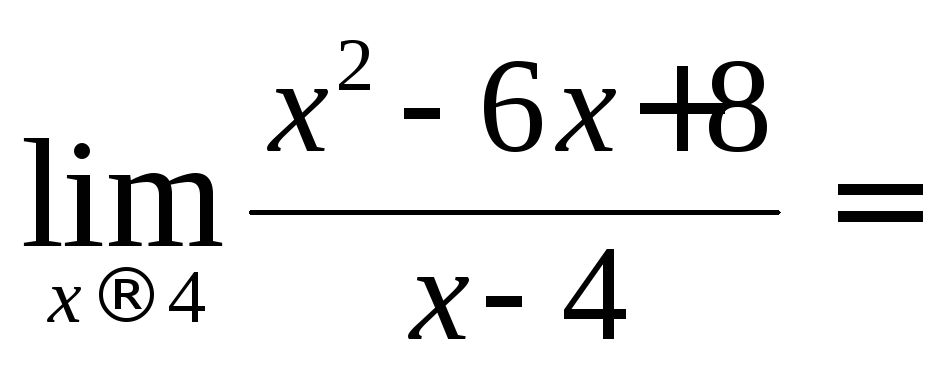 (по
замечанию 4)
(по
замечанию 4)

При
![]() числитель и знаменатель данной функции
обращаются в нуль. Получается
неопределенность вида
числитель и знаменатель данной функции
обращаются в нуль. Получается
неопределенность вида![]() ,
которая по замечанию 8 раскрывается
путем сокращения на критический множитель
. Разложим числитель на множители по
формуле
,
которая по замечанию 8 раскрывается
путем сокращения на критический множитель
. Разложим числитель на множители по
формуле![]() ,
где
,
где![]() и
и![]() корни квадратного уравнения
корни квадратного уравнения![]() .
Получим,
.
Получим,![]()
![]()
Здесь критический множитель находим умножением числителя и знаменателя на выражение сопряженное числителю:
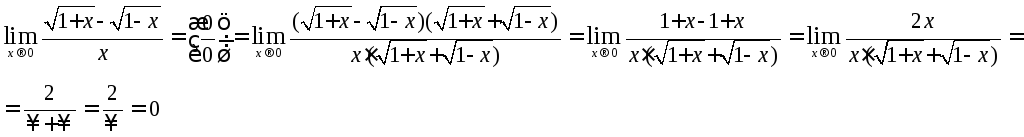
Замечание 9 Чтобы
раскрыть неопределенность
![]() надо путем преобразований получить
неопределенность вида
надо путем преобразований получить
неопределенность вида![]() или
или![]() .
.
![]() Пример 9
Вычислить
пределы:
Пример 9
Вычислить
пределы:
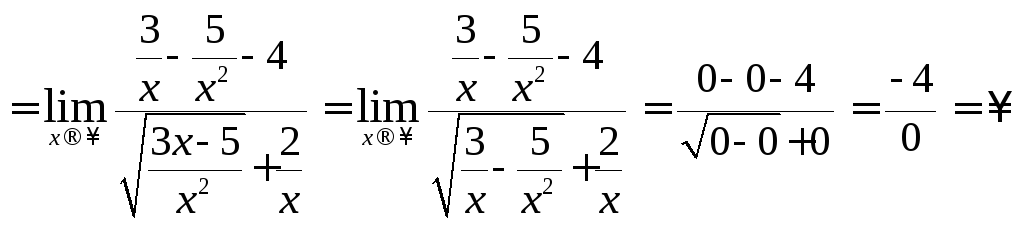
![]()
Задачи для выполнения на практических занятиях
Задачи для самостоятельного решения:
§ 4. Бесконечно малые величины и их применение к отысканию пределов
Определение.
Функция
![]() называетсябесконечно
малой величиной при
называетсябесконечно
малой величиной при
![]() ,
или
,
или![]() ,
если ее предел равен нулю:
,
если ее предел равен нулю:![]()
Например, функции
![]() при
при![]() и
и![]() при
при![]() есть бесконечно малые величины, ибо их
пределы равны нулю.
есть бесконечно малые величины, ибо их
пределы равны нулю.
Определение.
Пусть функции
![]() и
и![]() - бесконечно малые при
- бесконечно малые при![]() . Если
. Если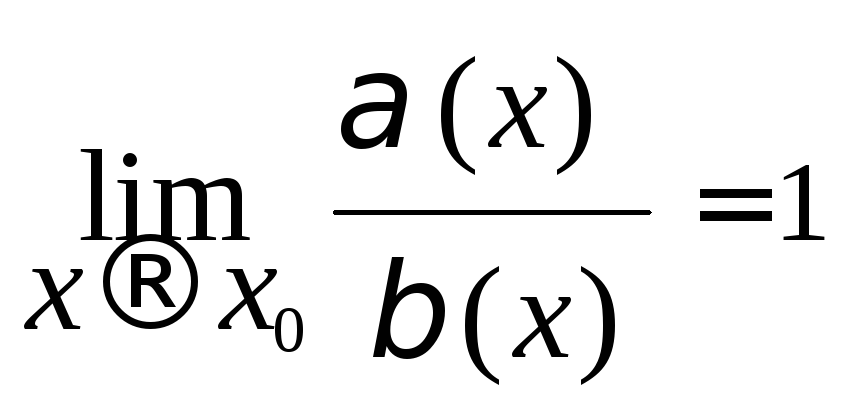 ,то
бесконечно малые
,то
бесконечно малые![]() и
и![]() при
при![]() называются
эквивалентными:
в этом случае пишут
называются
эквивалентными:
в этом случае пишут
![]() .
.
Если
![]() и
и
![]() ,
то справедлив принцип замены эквивалентных
бесконечно малых величин:
,
то справедлив принцип замены эквивалентных
бесконечно малых величин:![]()
Таблица эквивалентных бесконечно малых функций :
![]() Пример 10
Вычислить
пределы:
Пример 10
Вычислить
пределы:
При подстановке
вместо х значение 0 возникает
неопределенность вида
![]() .
Для нахождения критического множителя
воспользуемся таблицей эквивалентных
бесконечно малых функций. Т.к.
.
Для нахождения критического множителя
воспользуемся таблицей эквивалентных
бесконечно малых функций. Т.к.
![]() и
и
![]() ,
то функции
,
то функции![]() и
и![]() - бесконечно малые, значит
- бесконечно малые, значит![]() .
Аналогично
.
Аналогично![]() .
.
![]()
Задачи для выполнения на практических занятиях:
Задачи для самостоятельного решения: