
- •Пределы и непрерывность
- •Глава 1. Пределы числовых последовательностей и функций.
- •§ 1. Числовая последовательность и ее предел
- •§ 2. Предел функции в бесконечности и в точке
- •§ 3. Основные теоремы о пределах. Вычисление пределов функций
- •§ 4. Бесконечно малые величины и их применение к отысканию пределов
- •§5. Замечательные пределы
- •Глава 2. Непрерывность функции. Точки разрыва. Их классификация
- •§1. Непрерывные функции. Односторонние пределы
- •§2. Точки разрыва и их классификация
- •Контрольная работа
§5. Замечательные пределы
Определение.
Первым
замечательным пределом
называется
![]()
Кроме того,
![]() . Докажем это. Положим
. Докажем это. Положим
![]() ,
откуда
,
откуда![]() .
Если
.
Если![]() ,
то и
,
то и![]() ,
поэтому
,
поэтому .
.
Также
![]() Докажем
это. Разделив числитель и знаменатель
на
Докажем
это. Разделив числитель и знаменатель
на![]() ,
на основании формулы
,
на основании формулы
![]() получаем:
получаем:
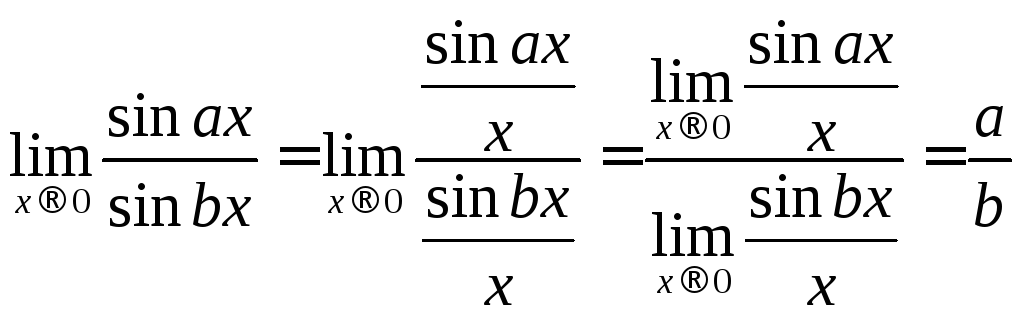 .
.
![]() Пример
12 Вычислить
пределы
Пример
12 Вычислить
пределы
a)![]() .
.
![]() Решение:
Решение:
Принимая во
внимание, что
![]() и
и![]() ,
на основании свойств пределов получаем
,
на основании свойств пределов получаем![]() .
.
Итак,
![]() .
.
b)
![]() .
.
![]() Решение:
Решение:
При
![]() числитель и знаменатель обращаются в
нуль. Знаменатель содержит иррациональность.
Освободимся от иррациональности
числитель и знаменатель обращаются в
нуль. Знаменатель содержит иррациональность.
Освободимся от иррациональности![]()
c)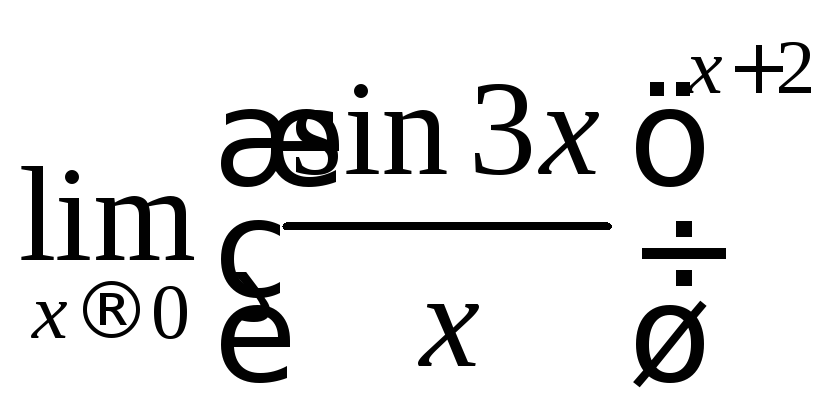
![]() Решение:
Решение:
Это предел вида
![]() ,
где
,
где![]() ,
,![]() .Поэтому
в соответствии с формулой (6) из §3 ищем
.Поэтому
в соответствии с формулой (6) из §3 ищем![]() ,
,![]()
Получаем
 .
.
Определение.
Вторым
замечательным пределом
называется
![]() или
или
![]() .
.
![]() ,
т.е. число е
– иррациональное число .
,
т.е. число е
– иррациональное число .
Число
![]() (число Эйлера,
неперово число)
играет весьма важную роль в математическом
анализе. График функции
(число Эйлера,
неперово число)
играет весьма важную роль в математическом
анализе. График функции
![]() получил
название
экспоненты.
Широко используются логарифмы по
основанию
получил
название
экспоненты.
Широко используются логарифмы по
основанию
![]() ,
называемые
натуральными.
Натуральные логарифмы обозначаются
символом
,
называемые
натуральными.
Натуральные логарифмы обозначаются
символом
![]() .
.
Кроме того
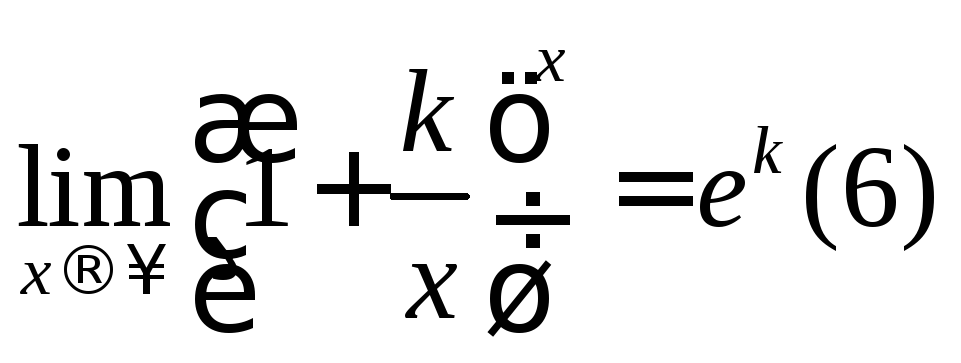 .
Докажем это.
.
Докажем это.
При
![]() выражение
выражение![]() ,
получаем неопределенность
,
получаем неопределенность![]() .
.
Введем новую
переменную
![]() по формуле
по формуле![]() ,
откуда
,
откуда![]() .
Если
.
Если![]() ,
то
,
то![]() ,
поэтому
,
поэтому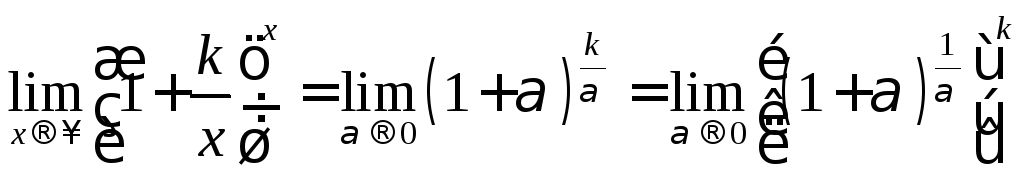 .
На основании формулы
.
На основании формулы![]() находим
находим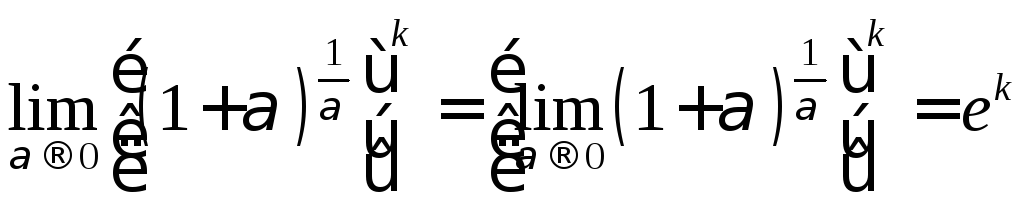 .
.
Следовательно,
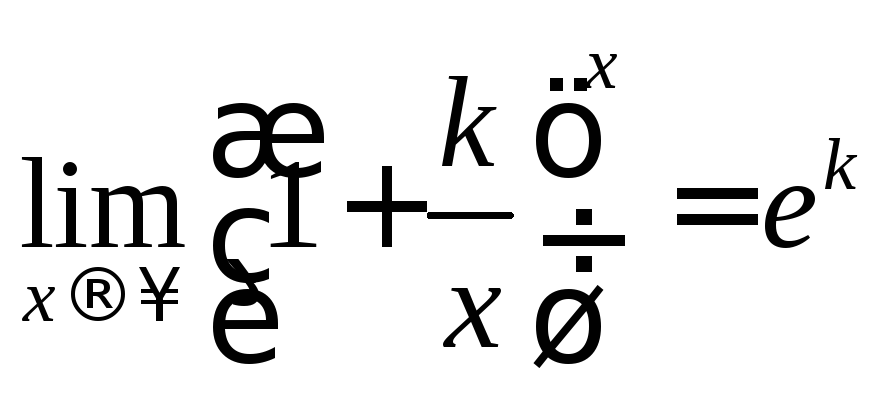 .
.
К пределам «типа
e»
относятся примеры с неопределенностью
вида
![]() .
В этом случае выражение, стоящее под
знаком предела, представляет собой
степенно-показательную функцию.
.
В этом случае выражение, стоящее под
знаком предела, представляет собой
степенно-показательную функцию.
Неопределенность устраняется при помощи выделения «второго замечательного предела».
![]() Пример
13 Найти
пределы:
Пример
13 Найти
пределы:
a)
![]() .
.
![]() Решение:
Решение:
![]()
На основании
формулы (5) получаем
![]() .
.
b)
![]() .
.
![]() Решение:
Решение:
![]()
Прибавляя и вычитая
1 из
![]() и применяя формулу (5), получаем
и применяя формулу (5), получаем
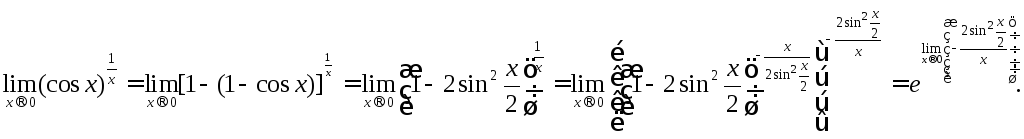
Поскольку
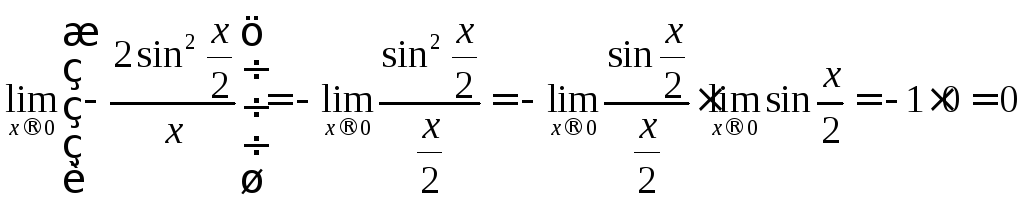 ,
то
,
то![]() .
.
c)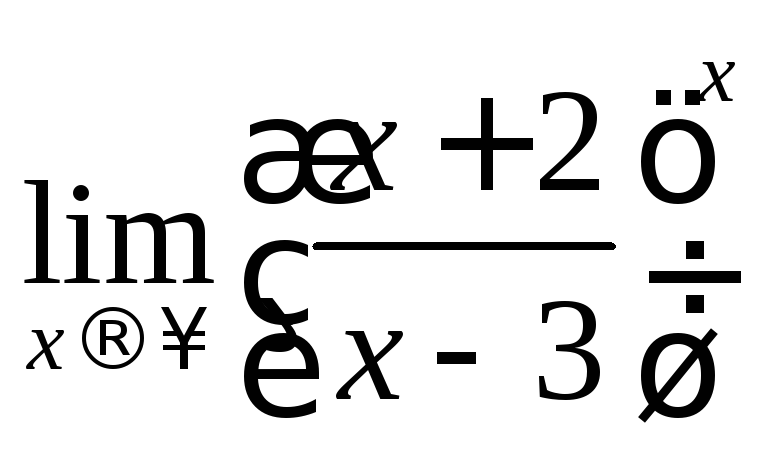 .
.
![]() Решение:
Решение:
Аналогично примеру
12c),
попробуем вычислить этот предел по
формуле
![]()
 .
Получаем
.
Получаем
![]() -
это предел «типаe».
-
это предел «типаe».
Получим
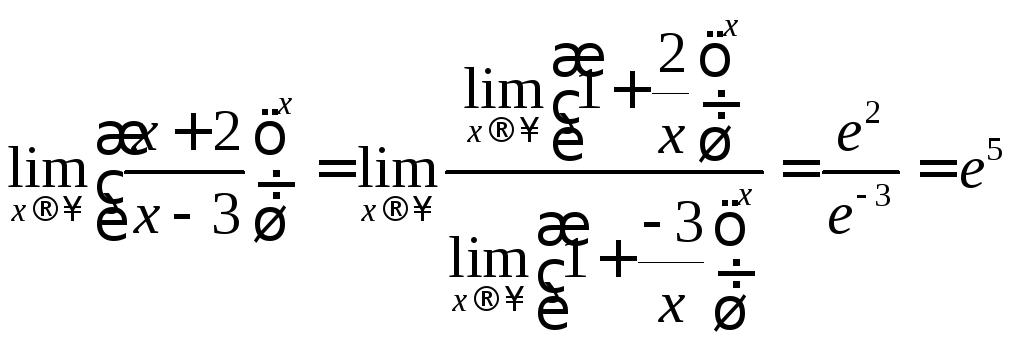 .
.
d)
![]() .
.
![]() Решение:
Решение:
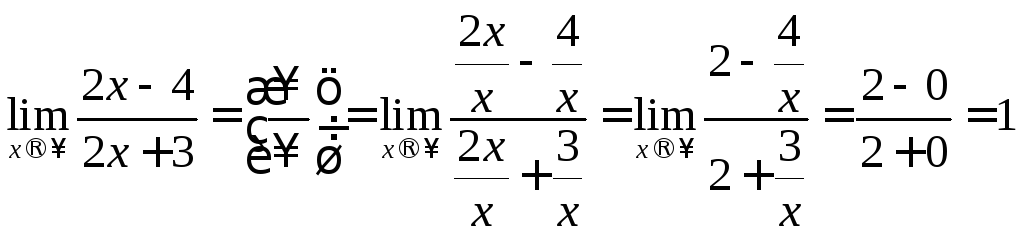 .
.
![]() .
.
Получим
![]() .
Значит это предел «типаe».
.
Значит это предел «типаe».
Решение получается сведением к формуле (6) путем прибавления к основанию 1 и введения новой переменной.
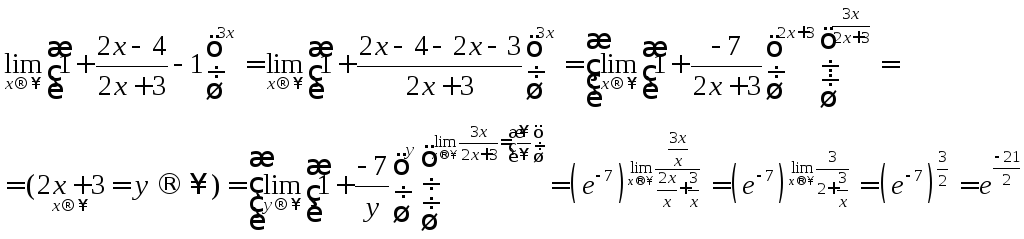
Замечание 10 При вычислении пределов степенно-показательных функций приходится также иногда пользоваться формулами
![]() и
и
![]() .
.
![]() Пример
14 Вычислить
пределы
Пример
14 Вычислить
пределы
a)
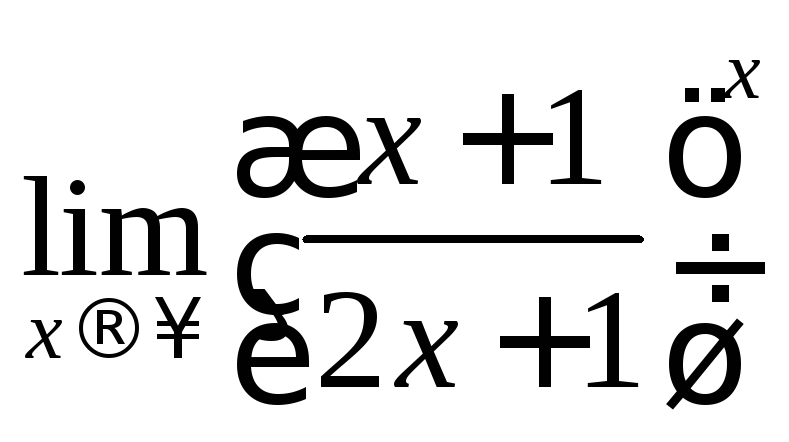 .
.
![]() Решение:
Решение:
 ,
поэтому
,
поэтому
 по
формуле
по
формуле![]() .
.
b)
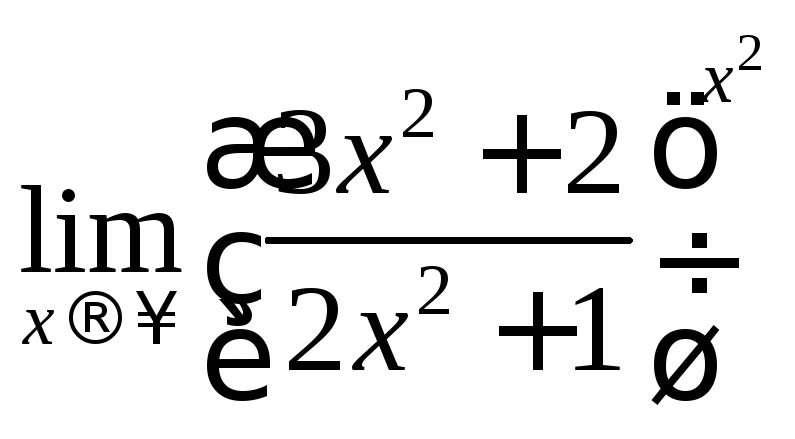 .
.
![]() Решение:
Решение:
 ,
поэтому
,
поэтому
 по формуле
по формуле![]() .
.
Задачи для выполнения на практических занятиях:
1)
![]()
2)
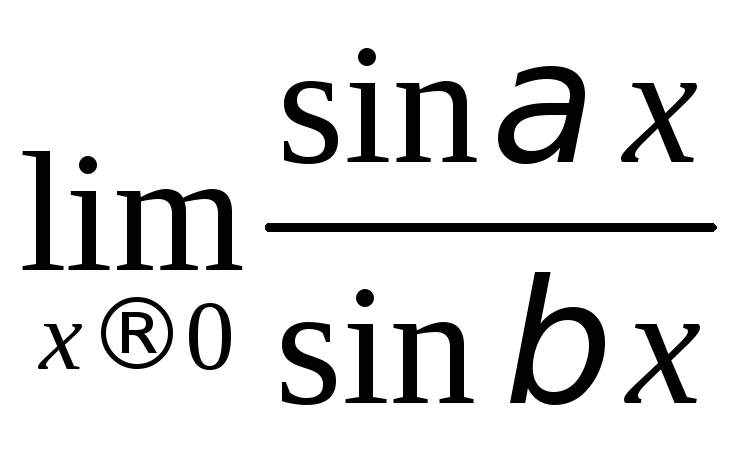
3)
![]()
4)

5)
![]()
6)
![]()
7)
![]()
8)

9)
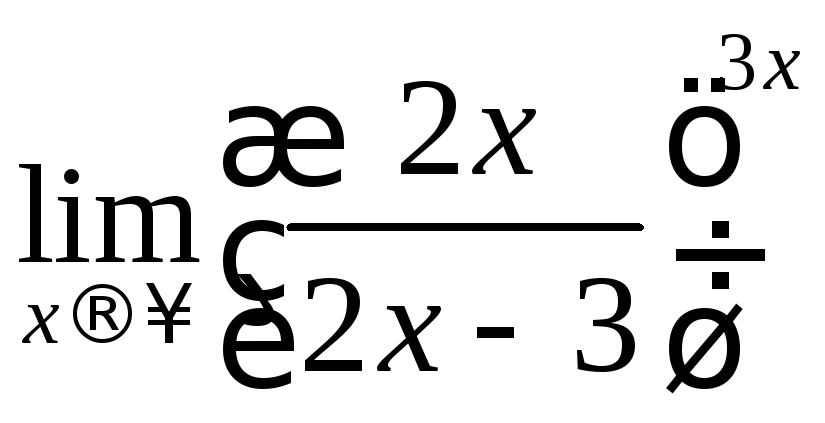
10)
![]()
11)
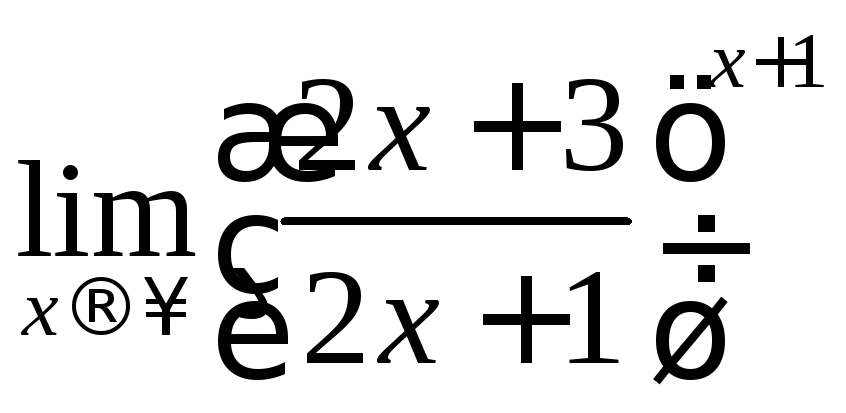
12)
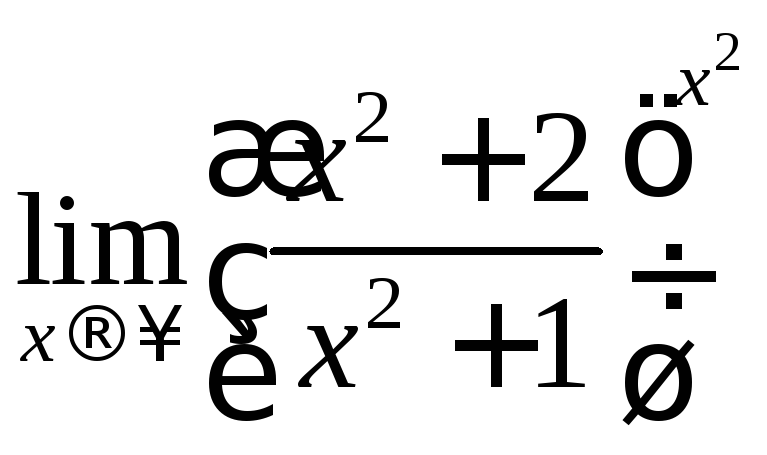
Задачи для самостоятельного решения:
Вычислить пределы:
1)
![]()
2)
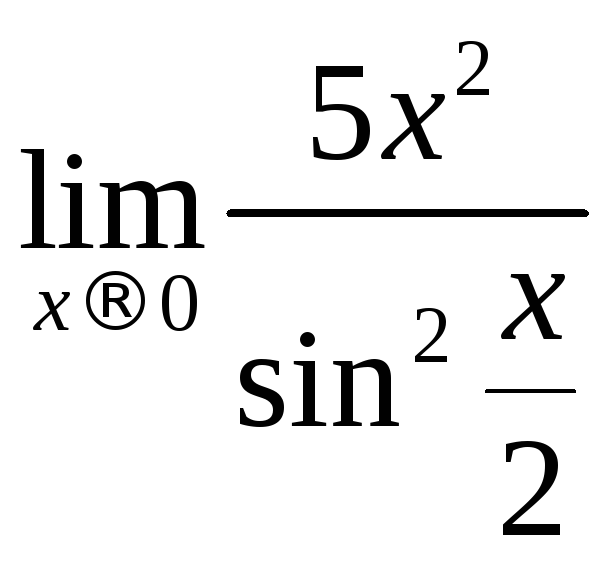
3)
![]()
4)
![]()
5)
![]()
6)
![]()
Тест
а)
-3
в)
![]() с)
с)
![]() d)
d)
![]() e)
e)
![]()
а)
![]() в)
3
с) 0
d) 1
e)
в)
3
с) 0
d) 1
e)
![]()
а)
0
в)
1
с
)
![]() d)
d)
![]() e)
e)
![]()
а) 0
в)
1 с)
![]() d)
d)
![]() e)
e)
![]()
О твет
твет
а)
0
в)
1
с) 2
d) 3
e)
![]()
О твет
твет
а)
-1
в)
0
с) 0,5
d) 1
e)
![]()
О твет
твет
а)
![]() в)
0 с)
0,5
d)
1
e)
в)
0 с)
0,5
d)
1
e)
![]()
