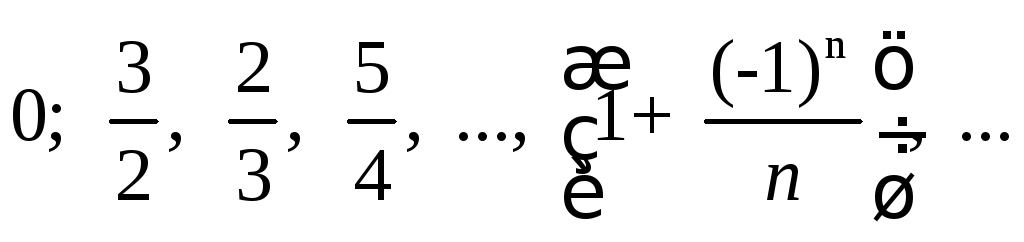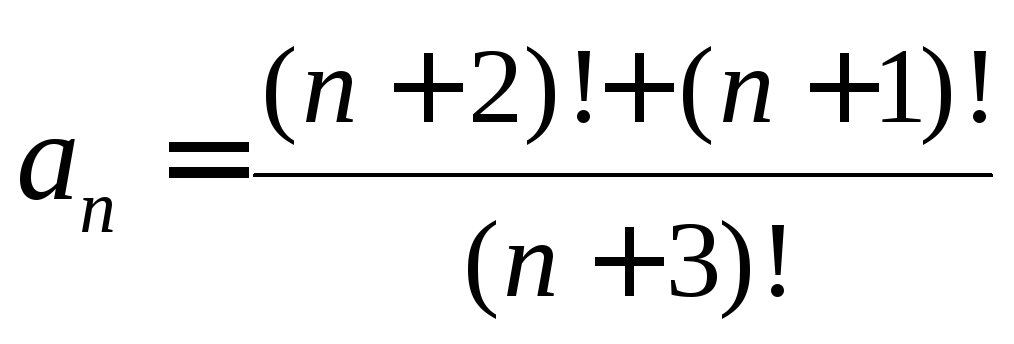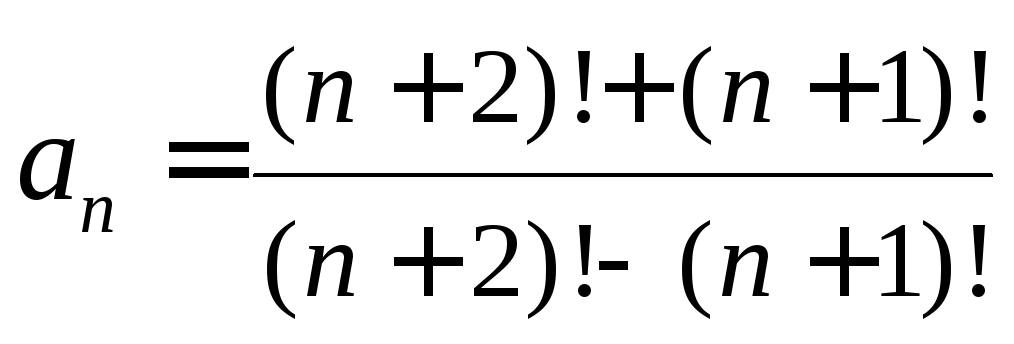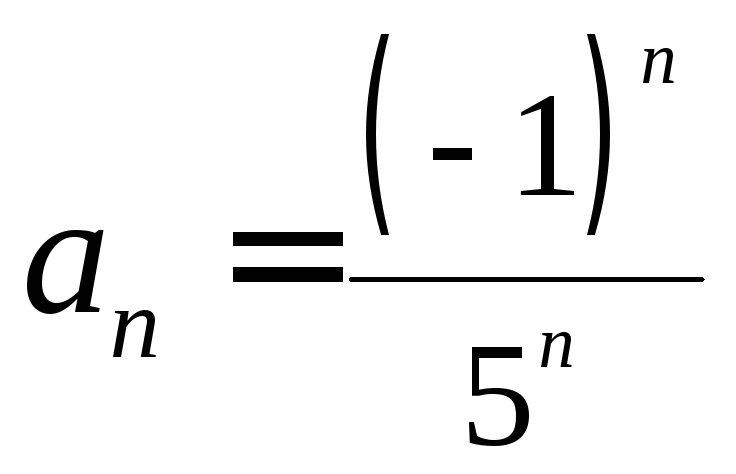- •Пределы и непрерывность
- •Глава 1. Пределы числовых последовательностей и функций.
- •§ 1. Числовая последовательность и ее предел
- •§ 2. Предел функции в бесконечности и в точке
- •§ 3. Основные теоремы о пределах. Вычисление пределов функций
- •§ 4. Бесконечно малые величины и их применение к отысканию пределов
- •§5. Замечательные пределы
- •Глава 2. Непрерывность функции. Точки разрыва. Их классификация
- •§1. Непрерывные функции. Односторонние пределы
- •§2. Точки разрыва и их классификация
- •Контрольная работа
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО «СЫКТЫВКАРСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ»
Математический факультет
Кафедра прикладной математики
Рабочая тетрадь
для проведения практических занятий
и обеспечения самостоятельной работы
по дисциплине «Математика» у студентов
специальностей и направлений подготовки
УГНС «Экономика и управление»
Научный руководитель
Зав. кафедрой,
профессор
___________В. Л. Никитенков
31.05.2011
Исполнитель,
студентка
135
гр.
____________А. В. Карышева
31.05.2011 .
Сыктывкар 2011
Консультант
Старший преподаватель
кафедры прикладной математики
___________Т. А. Тончева
31.05.2011
Исполнитель,
студентка
135
гр.
____________В. М. Кудрявых
31.05.2011 .
Содержание:
Введение
Основная часть:
Пределы числовых последовательностей и функций
Числовая последовательность и ее предел
Задания для выполнения на практических занятиях
Задания для самостоятельной работы
Предел функции в бесконечности и в точке
Задания для выполнения на практических занятиях
Задания для самостоятельной работы
Основные теоремы о пределах. Вычисление пределов функций
Задания для выполнения на практических занятиях
Задания для самостоятельной работы
Бесконечно малые величины и их применение к отысканию пределов
Задания для выполнения на практических занятиях
Задания для самостоятельной работы
Замечательные пределы
Задания для выполнения на практических занятиях
Задания для самостоятельной работы
Тест
Непрерывность функции. Точки разрыва. Их классификация
Непрерывные функции. Односторонние пределы
Задания для выполнения на практических занятиях
Задания для самостоятельной работы
Точки разрыва и их классификация
Задания для выполнения на практических занятиях
Задания для самостоятельной работы
Итоговая контрольная работа
Ответы к заданиям
Заключение
Литература
Введение
Курсовая работа методического характера
В рамках курсовой работы подготовлены разделы «Рабочей тетради» для проведения практических занятий по «Математике» у студентов, обучающихся по направлениям подготовки бакалавров укрупненной группы направлений подготовки и специальностей профессионального образования «Экономика и управление» В данной работе рассматривается вычисление пределов числовых последовательностей и функций.
Тема «Пределы и непрерывность » содержит разделы:
Пределы числовых последовательностей
Числовая последовательность и ее предел
Предел функции в бесконечности и в точке
Основные теоремы о пределах. Вычисление пределов функций
Бесконечно малые величины и их применение к отысканию пределов
Замечательные пределы
Непрерывность функций. Точки разрыва. Их классификация
Непрерывные функции. Односторонние пределы
Точки разрыва. Их классификация
Приведены теоретические сведения, включая формулировки основных теорем, свойств, правил, приведены формулы.
Подобраны задания для выполнения на практических занятиях
Подобраны задания для самостоятельной домашней работы
Разработаны тест и контрольная работа
Ко всем задачам в конце темы приведены ответы
Пределы и непрерывность
Глава 1. Пределы числовых последовательностей и функций.
§ 1. Числовая последовательность и ее предел
Определение.
Если по некоторому закону каждому
натуральному числу n
поставлено в соответствие вполне
определенное число
![]() то говорят, что задана
числовая последовательность
то говорят, что задана
числовая последовательность
![]() :
:![]()
Другими словами,
числовая
последовательность – это
функция натурального аргумента:
![]() .
.
Числа
![]() называютсячленами
последовательности,
а число
называютсячленами
последовательности,
а число
![]() -общим или
n-м
членом
данной последовательности.
-общим или
n-м
членом
данной последовательности.
Примеры числовой последовательности:
2, 4, 6, 8, … , 2n, …
3, 3, 3, 3, …
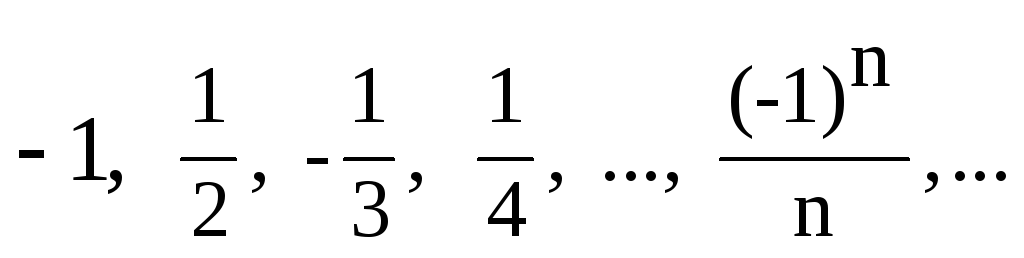
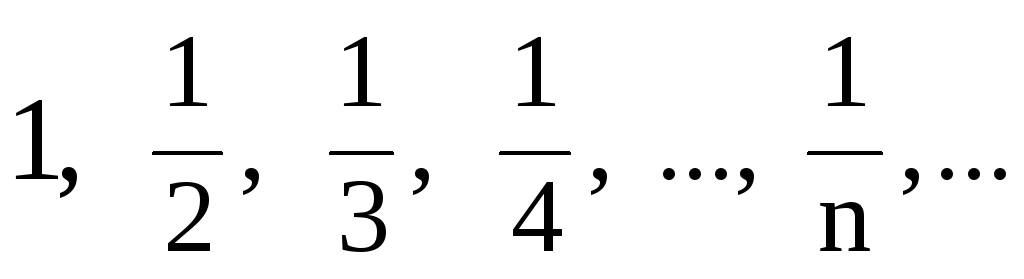
Рассмотрим числовую
последовательность:
![]() .
Изобразим ее члены точками числовой
оси.
.
Изобразим ее члены точками числовой
оси.
![]()
![]()
![]()
![]()
![]()
![]()







0
1
![]()
![]()
![]()
![]()
Можно заметить,
что члены последовательности
![]() с ростомn
как угодно близко приближаются к 0. При
этом абсолютная величина разности
с ростомn
как угодно близко приближаются к 0. При
этом абсолютная величина разности
![]() становится все меньше и меньше.
Действительно:
становится все меньше и меньше.
Действительно:![]() т.е.
с ростомn
т.е.
с ростомn
![]() будет меньше любого, сколь угодно малого
положительного числа.
будет меньше любого, сколь угодно малого
положительного числа.
Рассмотрим числовую
последовательность:
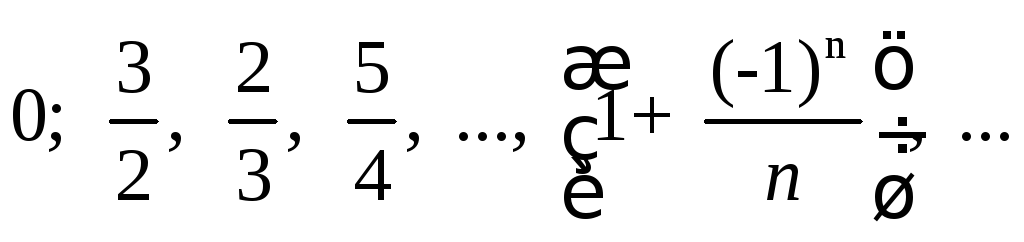 .
Изобразим ее члены точками числовой
оси.
.
Изобразим ее члены точками числовой
оси.
![]()
![]()
![]()
![]()
![]()
![]()
![]()












0
1
![]()
![]()
![]()
Можно заметить,
что члены последовательности
![]() с ростомn
как угодно близко приближаются к 1. При
этом абсолютная величина разности
с ростомn
как угодно близко приближаются к 1. При
этом абсолютная величина разности
![]() становится все меньше и меньше.
Действительно:
становится все меньше и меньше.
Действительно:![]() т.е.
с ростомn
т.е.
с ростомn
![]() будет меньше любого, сколь угодно малого
положительного числа.
будет меньше любого, сколь угодно малого
положительного числа.
Определение.
Число А
называется пределом числовой
последовательности
![]() ,
если для любого, сколь угодно малого
положительного числа
,
если для любого, сколь угодно малого
положительного числа
![]() ,найдется
такой номер N
(зависящий от
,найдется
такой номер N
(зависящий от
![]() ,
,![]() ),что для всех
членов последовательности с номерами
),что для всех
членов последовательности с номерами
![]() верно
неравенство:
верно
неравенство:
![]() .
.
Предел числовой
последовательности обозначается
![]() или
или![]() при
при![]() .
Последовательность, имеющая предел,
называетсясходящейся,
в противном случае – расходящейся.
.
Последовательность, имеющая предел,
называетсясходящейся,
в противном случае – расходящейся.
Используя логические
символы: квантор общности
![]() (вместо
слова «для любого») и квантор существования
(вместо
слова «для любого») и квантор существования![]() (вместо
слова «найдется»), символ равносильности
(вместо
слова «найдется»), символ равносильности![]() ,
определение предела можно записать в
виде
,
определение предела можно записать в
виде![]()
Смысл определения
предела числовой последовательности
состоит в том, что для достаточно больших
n
члены последовательности
![]() как угодно мало отличаются от числа А
(по абсолютной величине меньше, чем на
число
как угодно мало отличаются от числа А
(по абсолютной величине меньше, чем на
число![]() ,
каким бы малым оно ни было).
,
каким бы малым оно ни было).
![]() Пример
1
Пример
1
Доказать, что последовательность
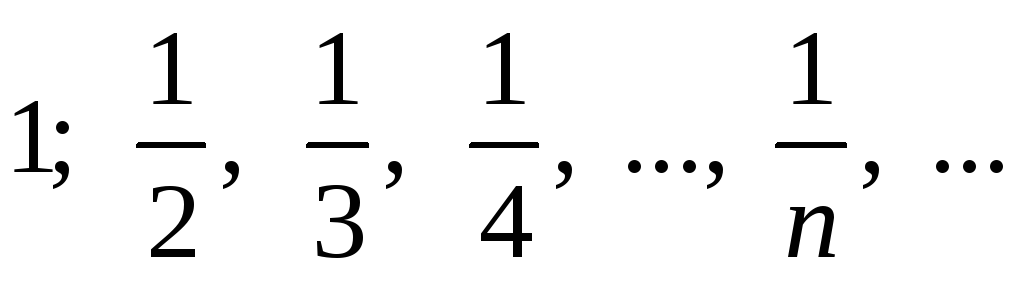 имеет предел равный нулю, т.е. требуется
доказать, что
имеет предел равный нулю, т.е. требуется
доказать, что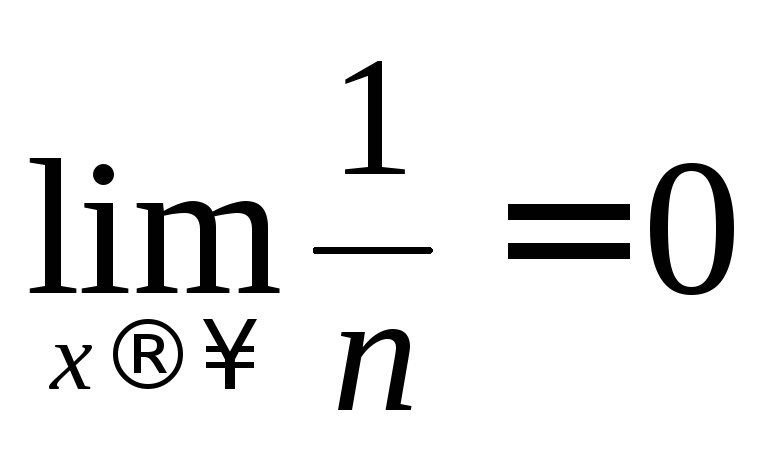
![]() Решение:
Найдем выражение для числа
Решение:
Найдем выражение для числа
![]() в зависимости от
в зависимости от![]() .
Для любого
.
Для любого![]() имеем
имеем![]() ,
или
,
или![]() .
Решая неравенство относительно
.
Решая неравенство относительно![]() ,
получаем
,
получаем![]() .
Итак, за
.
Итак, за![]() можно принять число
можно принять число![]() (или
любое большее число). Таким образом, для
любого
(или
любое большее число). Таким образом, для
любого![]() существует такое
существует такое![]() ,
что при
,
что при![]() выполняется неравенство
выполняется неравенство![]() ,
а это и означает, что
,
а это и означает, что![]() .
.
Доказать, что последовательность
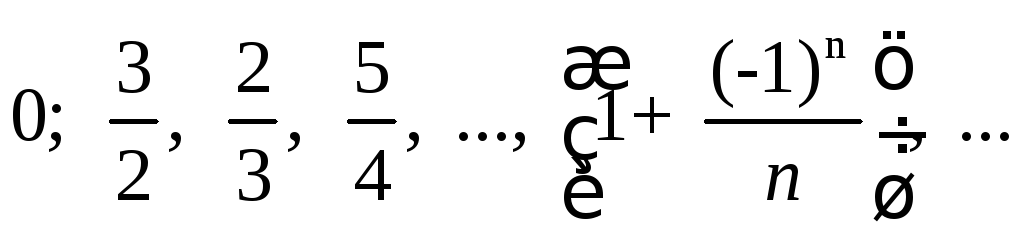 имеет предел равный единице, т.е.
требуется доказать, что
имеет предел равный единице, т.е.
требуется доказать, что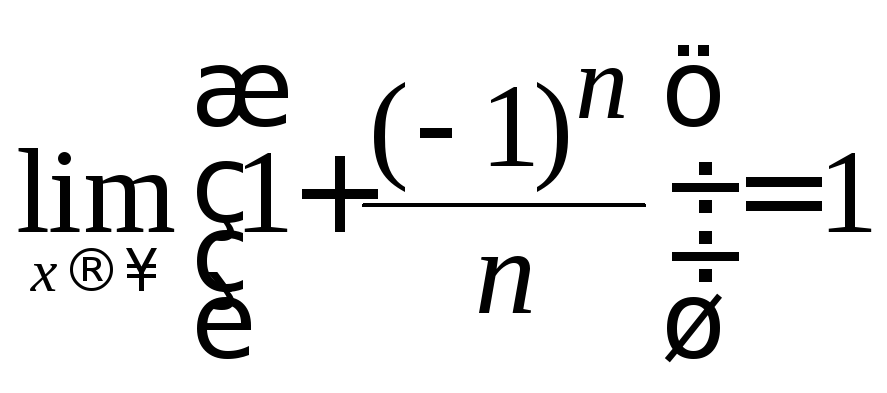
![]() Решение:
Пусть, Например,
Решение:
Пусть, Например,
![]() .
Тогда неравенство
.
Тогда неравенство![]() или
или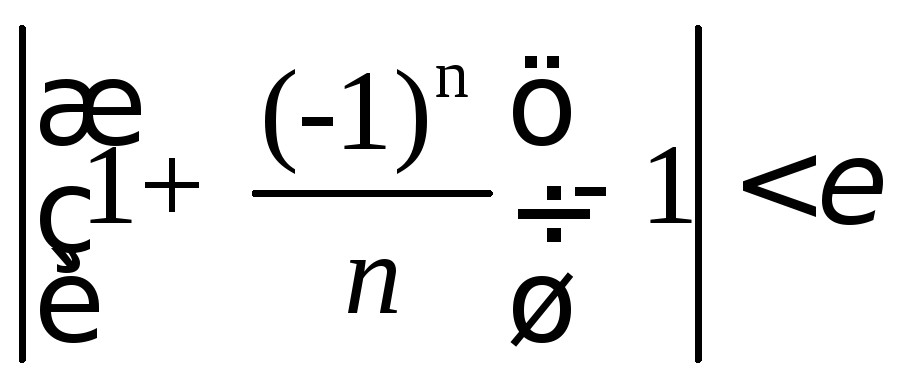 ,
т.е.
,
т.е.![]() выполняется при
выполняется при![]() .
Аналогично для
.
Аналогично для![]()
![]() при
при![]() .
.
Для любого
![]() неравенство
неравенство![]() или
или![]() выполняется при
выполняется при![]() .
.
Итак, при любом
![]() существует такой номер
существует такой номер![]() (или равный целой части
(или равный целой части![]() ),
что для всех
),
что для всех![]() (при
(при![]() для
для![]() ,
при
,
при![]() для
для![]() и т.д.) выполняется неравенство
и т.д.) выполняется неравенство![]() ,
а это и означает, что
,
а это и означает, что![]() .
.
Выясним геометрический смысл предела числовой последовательности.
Расположим
последовательности
![]() на числовой прямой. Неравенство
на числовой прямой. Неравенство
![]() равносильно двойному неравенству
равносильно двойному неравенству![]() ,
соответствующему попаданию
последовательности
,
соответствующему попаданию
последовательности![]() в
в![]() -окрестность
точки А.
-окрестность
точки А.
![]()
![]()

![]()











![]()
Итак, число
А есть предел числовой последовательности
![]() ,если для
любого
,если для
любого
![]() найдется
номер N,
начиная с которого (при
найдется
номер N,
начиная с которого (при![]() )все члены
последовательности будут заключены в
)все члены
последовательности будут заключены в
![]() -окрестности
точки А, какой бы узкой она ни была. Вне
этой
-окрестности
точки А, какой бы узкой она ни была. Вне
этой
![]() -окрестности
может быть лишь
конечное число членов
данной последовательности.
-окрестности
может быть лишь
конечное число членов
данной последовательности.
Вычисление пределов числовых последовательностей
Для сходящейся последовательности справедливы теоремы:
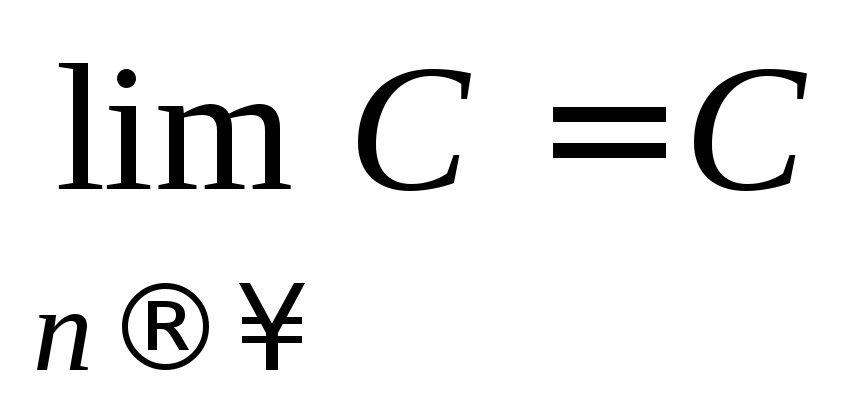 ,Где
,Где
 -
постоянная
-
постоянная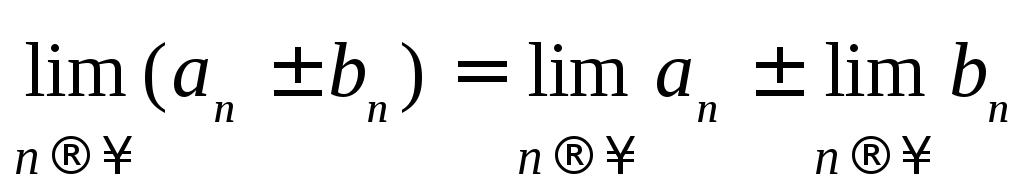
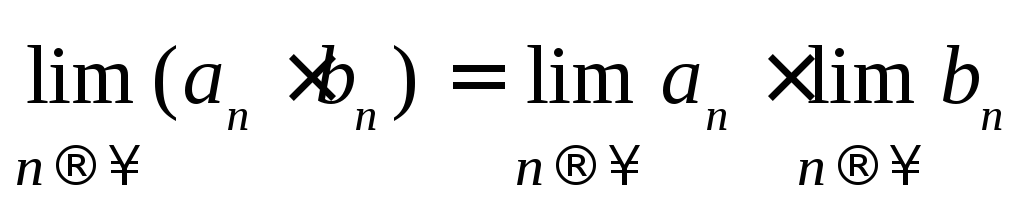 ,
,
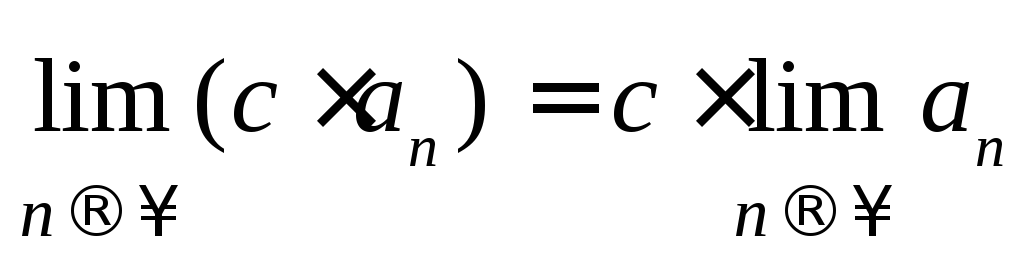
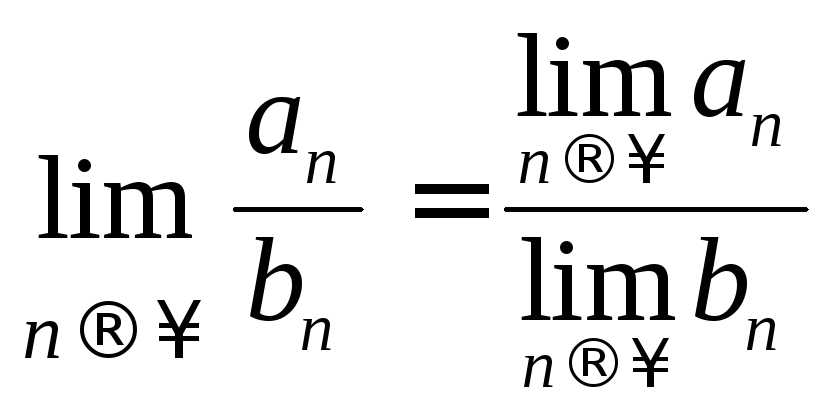 ,
,
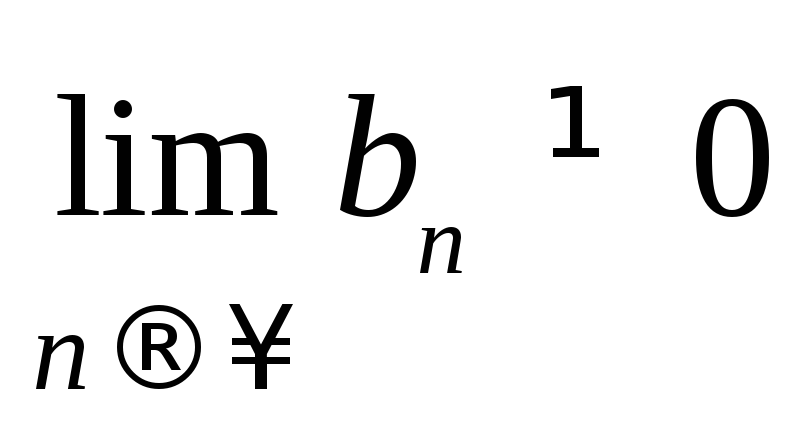
![]() Пример
2 Найти
предел последовательности с общим
членом
Пример
2 Найти
предел последовательности с общим
членом
![]() ,
т.е требуется найти
,
т.е требуется найти![]() .
.
![]() Решение:
Решение:
Преобразуем
выражение
![]() ,
поделив почленно числитель и знаменатель
на
,
поделив почленно числитель и знаменатель
на![]() и упростим сократив
на общий
множитель:
и упростим сократив
на общий
множитель:
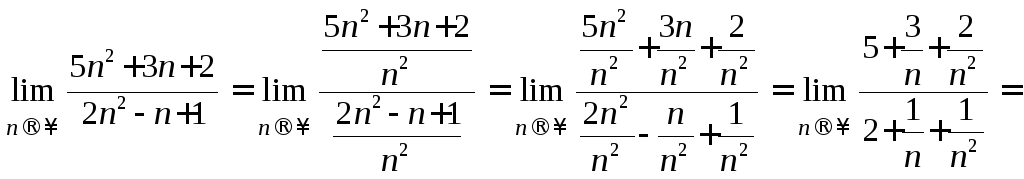 (по теореме 4)
(по теореме 4)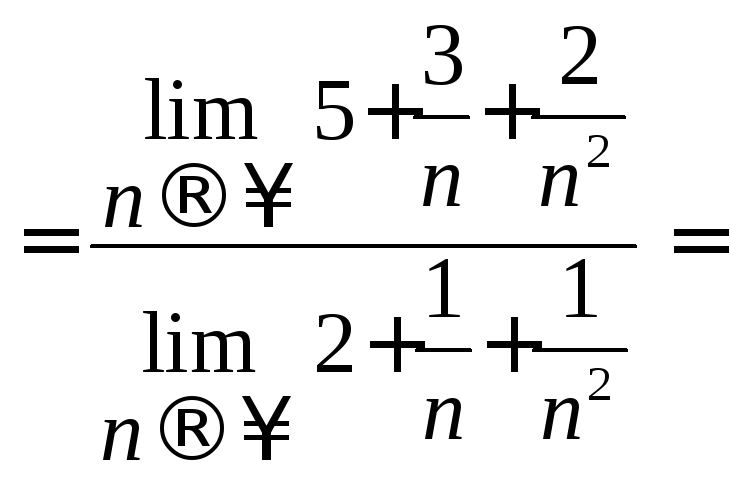 (по теореме 2)
(по теореме 2)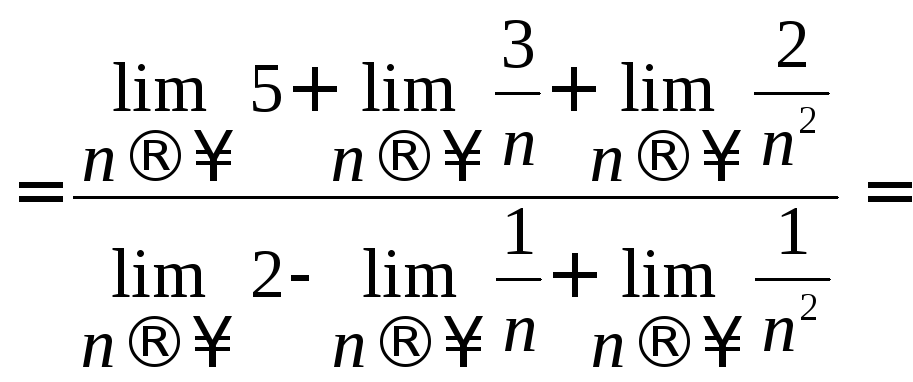 (
поскольку
(
поскольку![]() ,
получим)=
,
получим)=![]() ,
т.о.
,
т.о.![]()
Задачи для выполнения на практических занятиях
Найти предел последовательности:
Задачи для самостоятельного решения:
Найти предел последовательности:
Найти общий член последовательности: