7. Математические основы синтеза схем

Физическим аналогом букв двоичного алфавита (0 и 1) в схемах ЭВМ являются низкий и высокий потенциал, отсутствие и наличие импульса и т.п. Работу любой схемы ЭВМ можно представить следующим образом: на входы схемы поступает некоторая последовательность нулей и единиц, которая вызывает на выходах схемы вполне определенную последовательность нулей и единиц.

В настоящее время используются схемы двух классов: комбинационные (логические) и конечные (цифровые) автоматы (схемы с памятью).

В комбинационных схемах значения выходных сигналов в момент времени t однозначно определяются значениями входных сигналов в момент t1<=t.

В конечных автоматах выходные сигналы определяются не только и не всегда значениями входных сигналов в данный момент времени t, но и состоянием схемы, которое, в свою очередь, зависит от сигналов, поданных на ее входы в предыдущие моменты времени.

Сложные комбинационные (логические) схемы состоят из соединенных между собой определенным образом простейших схем - логических элементов. Выходной сигнал логического элемента однозначно определяется комбинацией входных сигналов (х1, х2, ... , хn), каждый из которых равен нулю или единице.

Поэтому каждый выходной сигнал может быть представлен в виде некоторой функции F (x1, x2, ... , xn), которая также принимает только два значения 0 и 1.

Таким образом, технические вопросы, связанные с составлением логических схем ЭВМ, можно решать с помощью математического аппарата, объектом исследования которого являются функции, принимающие, так же, как и их аргументы только два значения: ноль или единица. Таким аппаратом является математическая логика. Впервые такие функции были использованы в алгебре логики английским математиком Джоном Булем, поэтому они называются булевыми функциями.

При наличии в схемах элементов с памятью используется математический аппарат теории конечных автоматов, предложенный английскими математиками Мили и Муром.

7.1. Основы булевой алгебры. Булевы функции

Переменные, принимающие два значения: 0 и 1 (ложь и истина), называются булевыми (двоичными, логическими).

Основными операциями булевой алгебры является инверсия, конъюнкция и дизъюнкция.

Приоритет операций:

1. инверсия (НЕ), 2. конъюнкция(И), 3. дизъюнкция(ИЛИ).

Инверсия - логическое отрицание (НЕ). Обозначается как х (х', -x).

Таблица соответствия:

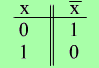
Конъюнкция - логическое умножение (операция И). Обозначается как x ^ y (x*y, x&y, xy).

Таблица соответствия:

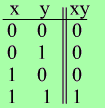
Дизъюнкция - логическое сложение (операция ИЛИ).

Обозначается как x ٧ y (x+y,xORy).

Таблица соответствия:

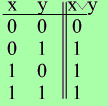
1. Отдельные переменные и константы в булевой алгебре являются логическими выражениями, например, 0 и 1 – это логические выражения.

2. Если А, В, ... являются логическими выражениями, то:

(А), (А)*(В), А*В, (А)٧ (В), ... – тоже логические выражения.

Для логических выражений булевой алгебры существует правило:

Два логических выражения равны, если они принимают равные значения на любом наборе значений их переменных.

Законы булевой алгебры.

Законы булевой алгебры можно выразить в виде формул:

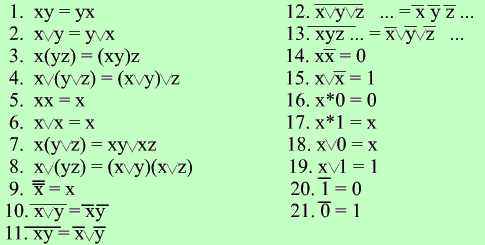
Удобно выделить законы, облегчающие преобразования формул к более простому виду, хотя они выводятся из ранее введенных.

Логические выражения булевой алгебры (булевы выражения) задают булевы функции, т.к. для каждого набора значений переменных булевого выражения можно определить значение всего выражения. При этом значение булевого выражения может быть либо 0, либо 1, как и значения исходных переменных.

Функция называется булевой, если она определена на всех наборах значений двоичных переменных, от которых зависит функция.

Булеву функцию всегда можно задать таблицей.

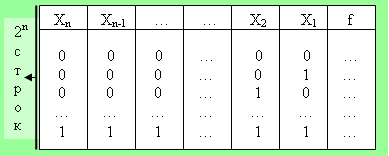
Для задания булевой функции необходимо знать множество наборов, при котором функция равна "1" –­­­­­ М1 (множество единичных наборов), либо множество наборов, на которых функция принимает значение "0" – множество М0.

Множество всех наборов значений n переменных обозначается "En".

Задав М1, известно, что М0 - это набор из En, не вошедший в М1 (и наоборот).

Выведем формулу для множества всех наборов значений n переменных. Пусть М1 - множество наборов, при котором функция равна "1", М0 - множество наборов, при котором функция равна "0", а En - множество всех наборов значений n переменных. Тогда Еn будет определяться как:

Наборы значений переменных булевых функций можно рассматривать как двоичные числа.

Например:

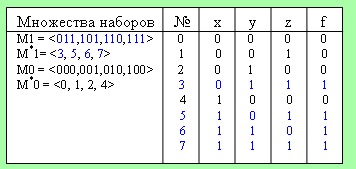
Часто вместо множества наборов значений аргументов булевых функций рассматриваются множества номеров наборов значений аргументов. При этом вместо М1 берется М*1 (как в примере с таблицей).

Функция может не зависеть существенно от некоторых переменных. По определению f (x1, x2, ... , x0, xn) не зависит существенно от xi, если на любом наборе переменных f (x1, x2, ... , 0, ... , xn) = f (x1, x2, ... , 1, ... , xn).

Пусть имеем две булевы переменные x и y. Количество различных сочетаний значений этих переменных равно 16. Соответственно для двух булевых переменных можно определить 16 булевых функций.

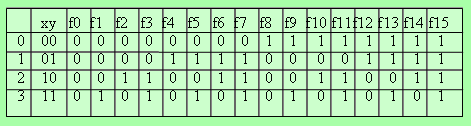
Ниже приведены названия этих булевых функций.