
Оценки экспертной комиссии группы С
..pdf
Пример 6.
В треугольнике ABC AB =15 , BC = 7 , AC = 9 . Точка D лежит на прямой BC так, что BD : DC = 2 : 3. Окружности, вписанные в каждый из треугольников ADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 6,5 или 3,7.
Комментарий.
Красивое, лаконичное и верное решение, хотя окружности лучше бы рисовать и покруглее.
Оценка эксперта: 3 балла.
41

Пример 7.
В треугольнике ABC AB =13 , BC = 7 , AC =11 . Точка D лежит на прямой BC так, что BD : DC =1: 7 . Окружности, вписанные в каждый из треугольниковADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF .
Ответ: 4,5 или 298 .
Комментарий. Какие-то умения по решению планиметрических задач автор явно демонстрирует, но их, очевидно, не хватает для выставления положительного балла.
Оценка эксперта: 0 баллов.
42

Пример 8.
В треугольнике ABC AB = 9 , BC = 5 , AC =8 . Точка D лежит на прямой BC так, что BD : DC = 3 : 7 . Окружности, вписанные в каждый из треугольниковADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF .
Ответ: 1,5 или 3.
Комментарий. Случай, аналогичный Примеру 7.
Оценка эксперта: 0 баллов.
43

Пример 9. |
AC =12 . Точка D лежит на прямой BC |
В треугольнике ABC AB =14 , BC =10 , |
|
так, что BD : DC =3: 7 . Окружности, |
вписанные в каждый из треугольников |
ADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 3 или 6.
Комментарий. План намечен довольно разумный и, наверное, реализуемый. Но, проверим, правда ли, что AD =13? Если это так, то
cos B = 9 +196 −169 |
=100 +196 −144 |
9 + 27 |
=152 . |
2 3 14 |
2 10 14 |
3 |
10 |
Неверно! Приведенные автором вычисления можно трактовать и как сознательную попытку «обмануть» проверяющего, и как честное обманывание самого себя, связанное с ошибками в вычислениях. Если судить «в пользу ученика», то – ясный 1 балл.
Оценка эксперта: 1 балл.
44
§5. Задания с развернутым ответом повышенного уровня сложности С5. Критерии проверки и оценки решений.
В этом параграфе представлены решения заданий С5 трех типов: из ЕГЭ–2010 (задача 1), ЕГЭ–2011 (задача 2) и ЕГЭ -2012 (задача 3). Все эти задачи - с параметром. В первой из них речь идет об исследовании поведения некоторой функции, во второй – о числе решений системы уравнений, в третьей – о числе корней уравнения
Как это обычно бывает, задачи с параметром допускают либо чисто алгебраический способ решения, либо способ решения, основанный на построении и исследовании геометрической модели. Для задач 1–3 геометрический метод решения быстрее и точнее ведет к цели.
Задача 1.
Найдите все значения a , при каждом из которых функция f (x)=x2 −2 | x −a2 | − 8x имеет более двух точек экстремума.
Решение. |
|
1. Функция f |
имеет вид: |
а) при x ≥ a2 : |
f (x)=x2 −10x + 2a2 , поэтому ее график есть часть параболы |
с ветвями, направленными вверх, и осью симметрии x =5 ; |
|
б) при x ≤ a2 : |
f (x)=x2 −6x −2a2 , поэтому ее график есть часть параболы с |
ветвями, направленными вверх, и осью симметрии x =3 .
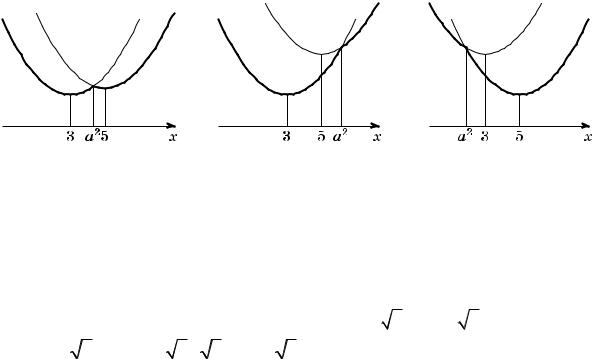
Все возможные виды графика функции f (x) показаны на рисунках:
Рис. 1 |
Рис. 2 |
Рис. 3 |
2. |
Графики обеих |
квадратичных функций проходят через точку |
(a2; f (a2 )) . |
|
|
3. |
Функция y = f (x) имеет более двух точек экстремума, а именно – три, |
|
в единственном случае (рис. 1): 3<a2 <5 3 < | a |< 5 . |
||
Ответ: − 5 < a < − 3; |
3 < a < 5 . |
|
45

Критерии оценивания выполнения задания С5, №3 |
Баллы |
|
|
|
|
Обоснованно получен правильный ответ |
4 |
|
|
|
|
Получен верный ответ. Решение в целом верное, но либо |
|
|
имеет пробелы (например, не описаны необходимые свойства |
3 |
|
функции), либо содержит вычислительные ошибки |
|
|
Верно рассмотрены все случаи раскрытия модулей. При |
|
|
составлении или решений условий на параметр допущены ошибки, |
2 |
|
в результате которых в ответе либо приобретены посторонние |
||
|
||
значения, либо часть верных значений потеряна |
|
|
|
|
|
Хотя бы в одном из случаев раскрытия модуля составлено |
|
|
верное условие на параметр либо построен верный эскиз графика |
1 |
|
функции в целом |
|
|
Решение не соответствует ни одному из критериев, |
0 |
|
перечисленных выше |
||
|
Подчеркнем, что приведенный критерий на 3 балла формально содержит внутреннее противоречие: «Получен верный ответ…» не сочетается с «…либо содержит вычислительные ошибки». Более точно, имелось в виду следующее:
«Решение в целом верное, но:
либо получен верный ответ, а обоснования имеют пробелы (например, не описаны необходимые свойства функции); либо в обосновании пробелов нет, но ответ неверен из-за вычислительных ошибок».
Задача 2.
Найдите все положительные значения a , при каждом из которых система
( |
|
x |
|
−6)2 +(y −12)2 = 4, |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
имеет единственное решение. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
+ y |
= a |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(x +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если |
|
x ≥0 , |
|
|
то |
уравнение |
|
|
|
|
y |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
( |
|
x |
|
−6) |
2 |
+(y −12) |
2 |
= 4 |
задаёт |
|
|
B |
2 |
|
|
|
B1 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
C2 |
|
|
12 |
C1 |
|
||||||||||||||
окружность |
ω1 |
|
с центром в точке |
|
|
|
|
|
|||||||||||||||||
|
|
ω2 |
A2 |
|
A1 |
ω1 |
|
||||||||||||||||||
C1 (6; 12) радиуса 2, а если x <0 , то |
|
|
|
|
|
|
|
ω |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
оно задаёт окружность ω2 |
с центром |
|
|
|
|
|
|
|
|
|
|||||||||||||||
в точке |
C2 (−6; 12) того же радиуса |
|
|
|
|
C |
|
|
|
|
|||||||||||||||
(см. рис.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
–6 |
–1 |
|
0 |
6 |
x |
|||||||||||||
При положительных значениях |
|
|
|
|
|
|
|
|
|
||||||||||||||||
параметра a уравнение |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(x +1)2 + y2 = a2 |
задаёт окружность ω |
|
|
|
|
|
|
|
ω |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

с центром в точке C (−1; 0) радиуса a . Поэтому задача состоит в том, чтобы
найти все значения параметра a , при каждом из которых окружность ω имеет единственную общую точку с объединением окружностей ω1 и ω2 .
Из точки C проведём луч CC1 и обозначим A1 и B1 точки его пересечения с окружностью ω1 , где A1 лежит между C и C1 . Так как
|
CC = (6 +1)2 +122 |
= 193 , то CA = |
193 −2, CB = 193 + 2 . |
||
|
1 |
|
1 |
1 |
|
|
При a < CA1 или a >CB1 окружности ω и ω1 не пересекаются. |
||||
|
При CA1 < a <CB1 окружности ω и ω1 имеют две общие точки. |
||||
|
При a =CA1 или a =CB1 окружности ω и ω1 касаются. |
||||
|
Из точки C проведём луч CC2 и обозначим A2 и B2 точки его |
||||
пересечения с |
окружностью |
ω2 , где A2 |
лежит между C и C2 . Так как |
||
CC = |
(−6 +1)2 |
+122 =13, то CA =13 −2 =11, CB =13 + 2 =15. |
|||
2 |
|
|
2 |
|
2 |
|
При a <CA2 или a >CB2 |
окружности ω и ω2 не пересекаются. |
|||
|
При CA2 < a <CB2 окружности ω и ω2 |
имеют две общие точки. |
|||
|
При a =CA2 или a =CB2 |
окружности ω и ω2 касаются. |
|||
Исходная система имеет единственное решение тогда и только тогда, когда окружность ω касается ровно одной из двух окружностей ω1 и ω2 и не
пересекается с другой. Так как CA2 <CA1 <CB2 <CB1 , то условию задачи удовлетворяют только числа a =11 и a = 193 +2 .
Ответ: 11; 193 + 2 .
Содержание критерия |
Баллы |
Обоснованно получен верный ответ |
4 |
С помощью верного рассуждения получены оба верных значения |
3 |
параметра, но |
|
– или в ответ включены также и одно-два неверных значения; |
|
– или решение недостаточно обосновано |
|
С помощью верного рассуждения получено хотя бы одно верное |
2 |
значение параметра |
|
Задача сведена к исследованию: |
1 |
– или взаимного расположения трёх окружностей; |
|
– или двух квадратных уравнений с параметром |
|
Решение не соответствует ни одному из критериев, перечисленных |
0 |
выше |
|
Максимальный балл |
4 |
47

Задача 3. Найдите все значения a , при каждом из которых уравнение
5 |
−3 |
= ax −2 на промежутке (0;+∞) имеет более двух корней. |
|||
x |
|
|
|
|
|
|
Решение. |
|
5 −3 |
|
|
|
Рассмотрим функции f (x )= ax −2 и g (x )= |
|
. Исследуем уравнение |
||
f (x )= g (x ) на промежутке (0; +∞). |
|
x |
|
||
|
|
|
|||
|
При a ≤0 все значения функции f (x ) на промежутке (0; + ∞) |
||||
отрицательны, а все значения функции g (x ) — неотрицательны, поэтому при a ≤0 уравнение f (x )= g (x ) не имеет решений на промежутке (0; +∞).
При a >0 функция f (x ) возрастает. Функция g (x ) |
убывает на |
|
|
|||||||
промежутке (0; |
5 |
, поэтому уравнение f (x )= g (x ) имеет не более одного |
||||||||
|
|
3 |
|
|
|
|
|
|
|
|
решения на промежутке (0; 5 |
, причём решение будет существовать тогда и |
|||||||||
только тогда, когда f ( |
3 |
|
|
|
|
|
|
|||
53 )≥ g ( |
53 ), откуда получаем a 53 −2 ≥ 0 , то есть a ≥ 56 . |
|||||||||
На |
промежутке |
(53 ; + ∞) |
уравнение f (x )= g (x ) принимает |
вид |
||||||
ax −2 =3 − 5 . Это уравнение |
сводится к |
уравнению |
ax 2 −5x +5 =0 . |
Будем |
||||||
|
x |
a >0, |
|
|
|
a ≤0 был |
|
|
|
|
считать, |
что |
поскольку случай |
рассмотрен |
ранее. |
||||||
Дискриминант квадратного уравнения D = 25 −20a , поэтому при a > 5 |
это |
|||||||||
|
|
|
|
|
|
при a = 5 |
|
|
4 |
|
уравнение не |
имеет |
корней; |
уравнение |
имеет единственный |
||||||
|
|
|
|
|
|
4 |
|
|
|
|
корень, равный 2; при 0 < a < 54 уравнение имеет два корня.
Если уравнение имеет два корня x |
1 |
и x |
2 |
, то есть 0 < a < 5 , то больший |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||
корень x2 = 5 + |
D > |
5 |
> 2 > 5 |
, поэтому он принадлежит промежутку |
|
|||||||||||||||
|
|
|||||||||||||||||||
|
|
2a |
2a |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(53 ; + ∞). Меньший корень x1 принадлежит промежутку (53 ; + ∞)тогда и |
||||||||||||||||||||
только тогда, когда |
3 ) |
|
( |
3 ) |
3 |
|
9 |
|
5 |
|||||||||||
|
( |
|
3 )( |
|
|
|
||||||||||||||
a |
|
x1 |
− 5 |
x2 − 5 |
= a |
|
5 |
2 −5 5 |
+5 = |
25a −30 |
>0 , то есть a > |
6 . |
||||||||
|
|
|
||||||||||||||||||
Таким образом, уравнение |
|
|
5 |
−3 |
|
= ax −2 |
имеет следующее количество |
|||||||||||||
|
|
|||||||||||||||||||
корней на промежутке (0; + ∞): |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
48
• |
нет корней при a ≤0 ; |
|
6 |
и a > 5 ; |
|
||
• |
один корень при 0 < a < |
|
|||||
|
|
|
|
5 |
4 |
|
|
• |
два корня при a = 6 и a |
= 5 ; |
|
||||
|
|
5 |
|
|
4 |
|
|
• |
три корня при 6 < a < |
5 . |
|
|
|
||
|
|
5 |
4 |
|
|
|
|
Ответ: 6 |
< a < 5 . |
|
|
|
|
||
|
5 |
4 |
|
|
|
|
|
|
|
Содержание критерия |
Баллы |
||||
Обоснованно получен правильный ответ |
4 |
||||||
С помощью верного рассуждения получено множество |
3 |
||||||
значений а, отличающееся от искомого конечным числом |
|||||||
точек |
|
|
|
|
|
|
|
С помощью верного рассуждения получены все граничные |
2 |
||||||
точки искомого множества значений а |
|||||||
|
|||||||
Верно получена хотя бы одна граничная точка искомого |
1 |
||||||
множества значений а |
|
|
|
||||
|
|
|
|
||||
Решение не соответствует ни одному из критериев, |
0 |
||||||
перечисленных выше |
|
|
|
||||
|
|
|
|
||||
|
|
|
|
|
Максимальный балл |
4 |
|
В решениях с ненулевыми баллами этого типа заданий чаще всего использовалась геометрическая модель. Из фиксированной на оси ординат точки проводились два луча: один – через точку «излома», другой – касательный к графику функции. Ответом являлся интервал между угловыми коэффициентами этих лучей. Так действовали многие, но большинство всетаки не получали оценки выше 1 балла.
Дело в том, что многие пропускали («это очевидно», «см. рис») проверку того, что абсцисса точки касания действительно лежит правее абсцисс точки излома, т.е., что изображенная картинка соответствует истинному положению дел. По критериям, только при наличии такой проверки можно было выставлять более 1 балла (хватало и просто явного указания абсциссы точки касания). Аналогично, при алгебраическом подходе для получения 2-х баллов недостаточно просто приравнять нулю дискриминант нужного квадратного уравнения: нужно еще указать, что соответствующий корень в самом деле больше абсциссы точки излома.
49

Примеры оценивания заданий С5.
Пример 1.
Найдите все значения a , при каждом из которых функция f (x)=x2 −| x −a2 | −9x имеет более двух точек экстремума.
(См. критерии задачи 1.)
Комментарий.
Ответ верен с точностью до странности 4 и описки − 2 , вместо
−2 = − 4 . В оригинале текста самое загадочное – это индексы у абсцисс вершин парабол. Фотоувеличение показывает, что это «extr» - экстремум. В остальном, - довольно ясно и прямо по критериям: «…Решение в целом верное, но либо имеет пробелы (например, не описаны необходимые свойства функции),…»
Оценка эксперта: 3 балла.
50
