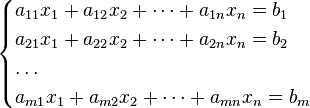4 Системы линейных алгебраических уравнений

Система m линейных алгебраических уравненийсn неизвестными (или, линейная система, также употребляется аббревиатураСЛА́У) в линейной алгебре— это система уравнений вида

Здесь — количество уравнений, а— количество неизвестных.x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^. Система линейных уравнений может быть представлена в матричной формекак:

Здесь — это матрица системы,— столбец неизвестных, а— столбец свободных членов. Если к матрицеприписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

5 Правило Крамера решения системы линейных уравнений

Метод Крамера

Система линейных уравнений:

Определители:

Решение:

6 Метод гаусса решения системы линейных уравнений

Ме́тод Га́усса^] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы

Алгоритм решени методом Гаусса подразделяется на два этапа.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме.

Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.

Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную наи, соответственно:

Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на:

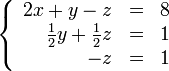
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

 из третьего;

 из второго, подставив полученное 

 из первого, подставив полученные и.

7 Матричный метод

Пусть для матрицы А порядка n на n существует обратная матрица . Умножим обе части матричного уравненияслева на(порядки матрицA ⋅ X и В позволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как, а по определению обратной матрицы(E – единичная матрица порядка n на n), поэтому

Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле . Другими словами, решение СЛАУ находится с помощью обратной матрицы.

Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУn ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.