1 Матрица

Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.

Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,..., ann .

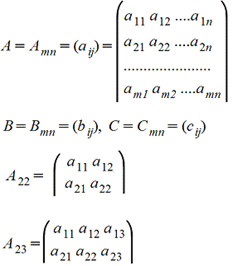
Действия над матрицами.

1. Сложение матриц - поэлементная операция

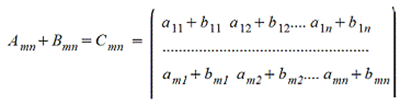
2. Вычитание матриц - поэлементная операция

3. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

4. Произведение матрицы на число - поэлементная операция

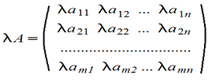
2 Определитель

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры.

Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.

Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определитель второго порядка вычислим, например, по элементам первой строки

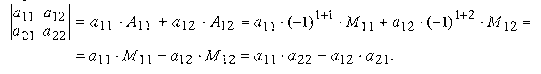
Запишем разложение данного определителя по элементам второй строки

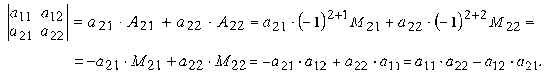
Полученный результат совпадает с результатом вычисления определителя по первой строке. Этот же результат получится и при разложении по любому из столбцов. Рекомендуем это проверить самостоятельно.

Из сказанного можно заключить, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

Пример

Найдем определитель третьего порядка, раскладывая его по элементам, например, третьего столбца

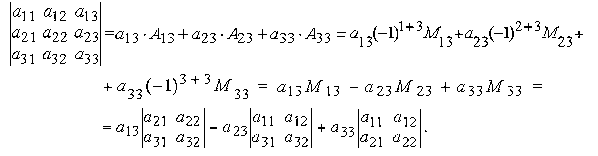
Пример.

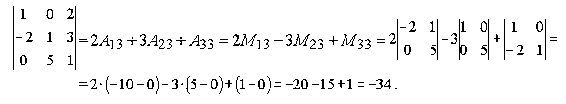
Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Получается, что определитель n - го порядка мы найдем через определители (n -1) - го порядка.

3 Обратная матрица

Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Свойства обратной матрицы

, где обозначает определитель.

для любых двух обратимых матрици.

гдеобозначает транспонированную матрицу.

для любого коэффициента.

Первый способ.

1. Вычислить определитель данной матрицы. Если, то обратной матрицы не существует (матрица вырожденная).

2. Составить матрицу из алгебраических дополненийэлементов матрицы 3. Транспонируя матрицу , получить присоединенную матрицу.

4. Найти обратную матрицу (4.1), разделив все элементы присоединенной матрицы на определитель

Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.(метод гаусса)

1. Составить блочную матрицу , приписав к данной матрицеединичную матрицу того же порядка.

2. При помощи элементарных преобразований, выполняемых над строками матрицы , привести ее левый блокк простейшему виду. При этом блочная матрица приводится к виду, где— квадратная матрица, полученная в результате преобразований из единичной матрицы.

3. Если , то блокравен обратной матрице, т.е.. Если, то матрицане имеет обратной.

В самом деле, при помощи элементарных преобразований строк матрицы можно привести ее левый блокк упрощенному виду(см. рис. 1.5). При этом блочная матрицапреобразуется к виду, где— элементарная матрица, удовлетворяющая равенству. Если матрицаневырожденная, то согласно п.2 замечаний 3.3 ее упрощенный вид совпадает с единичной матрицей. Тогда из равенстваследует, что. Если же матрица вырожденная, то ее упрощенный видотличается от единичной матрицы, а матрицане имеет обратной.