LARIONOV

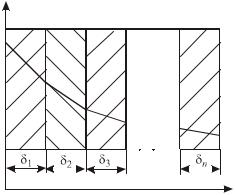
В случае стационарного процесса распространения теплоты тепловой поток, проходящий через каждый из слоев, будет одинаковым. Поэтому для каждого слоя имеем возможность записать:

для первого слоя

z

tc1

tc2

Рис.2.4. Теплопроводность через многослойную плоскую стенку

В соответствии с граничными условиями известной считается температура на наружных границах

PDF created with pdfFactory Pro trial version www.pdffactory.com

Сложив почленно последнее выражение, получим

На рис.2.4 в виде ломаной линии изображен график изменения температуры по толщине многослойной стенки.

Сумму термических сопротивлений всех n слоев ån δi называют полным термическим

i=1 λi

сопротивлением теплопроводности многослойной стенки.

Для сравнительного анализа процесса теплопроводности через стенку из однородного материала и многослойную стенку удобно пользоваться понятием эквивалентного коэффициента теплопроводности

многослойной стенки λэкв . Численно он равен коэффициенту теплопроводности такой условной

n

однородной (однослойной) стенки, толщина которой равна суммарной толщине многослойной стенки åδi

i=1

, а термическое сопротивление равно термическому сопротивлению многослойной стенки:

2.1.7. Теплопроводность в однослойной цилиндрической стенке

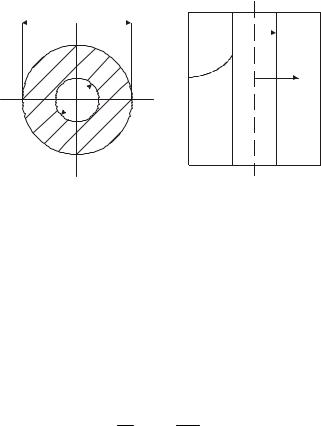
Рассмотрим процесс теплопроводности в однородной однослойной цилиндрической стенке бесконечной длины при граничных условиях первого рода (рис.2.5). Процесс теплопроводности считаем стационарным.

PDF created with pdfFactory Pro trial version www.pdffactory.com

d1

r1

r

d2

r2

tc2

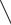tc1

Рис.2.5. Цилиндрическая однослойная стенка

В данном случае дифференциальное уравнение теплопроводности удобнее записать в цилиндрической системе координатах:

При заданных условиях процесса теплопроводности и при совмещении оси ОZ с осью цилиндра температура будет меняться только в радиальном направлении и температурное поле будет одномерным. Тогда

¶t = 0 и ¶2t = 0 . ¶z ¶z2

Поскольку температура на наружной и внутренней поверхностях цилиндра постоянна (заданы граничные условия первого рода), то изотермические поверхности будут цилиндрическими с осями, совпадающими с осью цилиндра. Следовательно, температура не будет изменяться и вдоль угловой

после интегрирования получим ln u + ln r = ln C1 .

Потенцирование и возвращение к первоначальной переменной приводит к результату

PDF created with pdfFactory Pro trial version www.pdffactory.com

r1

Таким образом, изменение температуры по толщине цилиндрической стенки происходит по логарифмическому закону.

Количество теплоты, проходящее через цилиндрическую поверхность F = 2πrl в единицу времени,

может быть найдено из совместного решения математического выражения закона Фурье и выражения (2.43).

Тогда

r1

Плотность теплового потока в случае цилиндрической стенки может быть определена путем отнесения

В практике теплотехнических расчетов также используют понятие линейной плотности теплового потока q1 как величины теплового потока, отнесенной к длине цилиндра:

потока не зависит от величины поверхности цилиндрической стенки. В то же время из выражения (2.48)

PDF created with pdfFactory Pro trial version www.pdffactory.com

легко определить, что плотность теплового потока, отнесенная к внутренней и внешней поверхности

Контрольные вопросы

1.Основные способы распространения теплоты в природе.

2.Что называется температурным градиентом?

3.Определение понятия теплового потока.

4.Физический смысл гипотезы (закона) Фурье, коэффициента теплопроводности.

5.Что такое коэффициент температуропроводности? Его физический смысл.

6.Что понимается под краевыми условиями (краевой задачей).

7.Виды граничных условий и их запись.

8.Процесс теплопроводности в однослойной стенке при граничных условиях первого рода.

9.Процесс теплопроводности в многослойной стенке.

10.Определение понятия термического сопротивления стенки.

11.Процесс теплопроводности в однослойной цилиндрической стенке при граничных условиях первого

рода.

12.Что понимается под линейной плотностью теплового потока?

2.2. Конвективный теплообмен

Как уже отмечалось, конвекция представляет собой перенос теплоты совместно с макроскопической массой жидкости в среде с неравномерным распределением температуры. Распространение теплоты посредством конвекции всегда сопровождается теплопроводностью. Такой теплообмен, обусловленный совместными процессами конвекции и теплопроводности, называется конвективным теплообменом.

Конвективный теплообмен между движущейся жидкостью и поверхностью, отделяющей эту жидкость от другой среды, называется теплоотдачей.

В качестве основного уравнения теплоотдачи используется уравнение Ньютона для плотности теплового потока:

являющегося границей раздела.

Коэффициент теплоотдачи определяет количество теплоты, которое передается от жидкости к поверхности тела площадью 1 м2 при разности температур жидкости и поверхности тела в 1 оС.

Уравнение (2.51) было получено в предположении, что теплообмен происходит в свободном потоке, а коэффициент теплоотдачи зависит только от физических свойств граничного тела и жидкой среды.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Как было установлено, коэффициент теплоотдачи, в отличие от коэффициента теплопроводности, не является постоянной величиной, а зависит от большого числа различных факторов: движущих сил конвекции (свободная или вынужденная), режима течения жидкости, размеров и формы границы раздела и ее теплофизических свойств, направления и скорости потока. Поэтому, строго говоря, плотность теплового потока может быть рассчитана по выражению (2.51) лишь после того, как будет определен коэффициент теплоотдачи, представляемый в общем случае функциональной зависимостью вида:

жидкости; ср - теплоемкость; β - коэффициент объемного расширения.

Теоретическое определение коэффициента теплоотдачи проводят путем математического моделирования процесса, составляя систему дифференциальных уравнений конвективного теплообмена, в которую входят уравнения энергии, движения и неразрывности. Конкретизация решаемой задачи проводится заданием условий однозначности. Однако получаемая в таких случая система дифференциальных уравнений, дополненная условиями однозначности, в большинстве случаев не интегрируется. Поэтому при решении практических инженерных задач используются данные, полученные экспериментальным путем. Вместе с тем для возможности обобщения таких данных, определения границ их

применения и определения возможности перенесения этих данных на схожие процессы теплоотдачи экспериментальные исследования должны опираться на строгие теоретические начала.

На современном этапе развития науки теоретической базой эксперимента помимо теории планирования эксперимента является теория подобия, которая позволяет, не интегрируя систему дифференциальных уравнений, сделать ряд важных выводов, необходимых для научной обработки результатов эксперимента. Понятие о подобии может быть распространено на любые физические явления при условии, что:

·эти физические явления принадлежат к одному классу явлений;

·имеется геометрическое подобие систем, в которых эти явления протекают;

·при рассмотрении подобных явлений сопоставляются только одноименные физические величины в сходственных точках пространства и в сходственные моменты времени.

Наиболее простым примером подобия является геометрическое подобие, при котором отношение

линейных размеров любых сходственных сторон двух подобных фигур равно некоторой постоянной величине - константе подобия с.

В подобных физических явлениях в сходственных точках пространства и в сходственные моменты времени любая величина e¢ первого явления пропорциональна одноименной величине e² второго явления:

где cε - константа физической величины e.

Предположим, что исследуется некоторый класс явлений, происходящие процессы в котором

описываются уравнением

f (ε1,ε2 ,...εn ) = 0 ,

где ε1,ε2 ,...εn - переменные физические величины исследуемого класса явлений.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Пусть в двух независимых системах происходят процессы, принадлежащие к исследуемому классу явлений. Тогда имеем право записать

f1 (ε1' ,ε'2...ε′n ) = 0,

(2.54)

f2 (ε1" ,ε''2 ,...ε"n ) = 0.

Для подобия процессов, происходящих в обеих системах, должно выполняться условие (2.53)

Видно, что каждая переменная имеет свою константу подобия, отличную по величине от других, но при этом константы подобия между собой находятся в вполне определенных соотношениях. Тогда систему уравнений (2.54) можно представить в виде

f1 (ε1′, ε2′,...εn′ )= 0,

(2.56)

f2 (cε1 ε1′, cε2 ε2′,...cεn εn′ )= 0.

Причина ограничения произвольности выбора значений констант подобия в том, что сами физические величины, определяющие характер протекания процесса, между собой связаны вполне определенными уравнениями, вытекающими из основных законов природы.

Для того чтобы установить условие, ограничивающее выбор констант подобия, рассмотрим движение

жидкости со скоростью V на пути l за время τ : V = τl . Для сходственных частиц двух потоков имеем

является тем условием, которое ограничивает произвольность выбора констант подобия при рассмотрении сложных физических явлений. Если вместо констант подобия подставить характеризуемые ими величины,

то

где « idem » означает «одно и то же», т.е. критерии подобных явлений должны быть одинаковыми.

С использованием этих уравнений и входящих в них размерных физических величин можно получить некие безразмерные комплексы, которые принято называть критериями (числами) подобия.

Критерий подобия - это безразмерное число, составленное из размерных физических величин,

определяющих анализируемое физическое явление и сохраняющее одно и то же числовое значение для всех подобных между собой явлений. С физической точки зрения критерий подобия выражает соотношение между различными физическими эффектами, характеризующими данное явление.

В теории подобия выделяют два вида критериев:

-определяющие - критерии, составленные из величин, заданных при математическом описании процесса;

-определяемые - критерии, в состав которых входит определяемая величина процесса.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Поскольку для процесса теплоотдачи определяемой величиной является коэффициент теплоотдачи, то критерий подобия, содержащий в своем составе коэффициент теплоотдачи, есть определяемый критерий.

Практическое применение теории подобия базируется на трех теоремах.

1.У подобных явлений одноименные критерии подобия равны.

2.Критерии подобия, полученные из дифференциальных уравнений, описывающих анализируемый процесс, одновременно являются и критериями подобия, получаемыми в результате решения (интеграла) этих уравнений.

Таким образом, решение дифференциального уравнения (без процесса интегрирования) может быть представлено как функция от критериев подобия. Если же решить исходное дифференциальное уравнение, то после решения не могут появиться какие-либо новые критерии подобия и пропасть критерии, получаемые из дифференциальных уравнений.

Данной теореме может быть придан другой смысл: определяющие Ко и определяемые критерии Коп подобных процессов связаны между собой уравнением подобия (так называемое критериальное уравнение), которое является безразмерным решением рассматриваемой задачи, справедливым для всех подобных процессов. В общем виде критериальное уравнение имеет вид

Из данной теоремы вытекает, что можно, не интегрируя дифференциальные уравнения исследуемых процессов, получать расчетные формулы путем замены исходных дифференциальных уравнений критериальными.

3. Поскольку из всего многообразия процессов, принадлежащих к рассматриваемому классу явлений, данный процесс определяется заданием условий однозначности, то обязательной предпосылкой к подобию сравниваемых процессов является подобие условий однозначности.

Поэтому третья теорема говорит о том, что подобны те явления, условия однозначности которых подобны, а критерии подобия, составленные из условий однозначности, равны.

2.2.1.Критерии подобия и критериальные уравнения

Всоответствии с физической природой конвективного теплообмена в подобных системах в основном рассматриваются гидродинамическое и тепловое подобие.

Для нахождения условий и критериев гидродинамического подобия двух потоков вязкой жидкости используется система уравнений Навье - Стокса. Из дифференциальных уравнений, входящих в систему, получают следующие критерии подобия (без вывода):

давления в потоке жидкости к динамическому напору потока (характеризует соотношение сил давления и сил инерции в потоке);

PDF created with pdfFactory Pro trial version www.pdffactory.com

жидкости при свободной конвекции, являясь отношением подъемной силы, возникающей из-за разности плотностей жидкости, и сил вязкости в неизотермическом потоке. Здесь l - характерный размер потока; β -

температурный коэффициент объемного расширения жидкости; t - разность температур в различных точках потока жидкости.

Для гидродинамического подобия критерий Эйлера является определяемый, давление (перепад давления) является функцией процесса, т.е. искомой величиной, не входящей в условия однозначности. Все остальные критерии - определяющие. Тогда в общем случае критериальное уравнение будет иметь вид

В случае напорного потока жидкости критерий Фруда исключается из числа, входящих в рассмотрение, из-за малого влияния сил тяжести на поле скоростей и давлений. В этом случае критериальное уравнение

для стационарного вынужденного потока жидкости примет вид

При естественной конвекции число Фруда необходимо учитывать, но поскольку движущей силой в этом случае является разность плотностей в смежных точках потока, вместо критерия Фруда целесообразнее использовать критерий Грасгофа.

При тепловом подобии определяются критерии подобия температурных полей и тепловых потоков.

Непременным условием теплового подобия является геометрическое и гидродинамическое подобия систем.

Из дифференциального уравнения конвективного теплообмена и условий теплоотдачи на границе тела для двух подобных систем выводятся следующие критерии (числа) теплового подобия:

теплопроводного и конвективного переноса теплоты в потоке;

∙Fo = alt - критерий (число) Фурье (безразмерное время), где l - характерный размер тела. Данный

критерий характеризует связь между скоростью изменения температурного поля, физическими константами и размерами тела, являясь мерой скорости изменения температурного поля при нестационарном режиме;

характеризующий физические свойства жидкости и способность распространения в ней теплоты;

∙Nu = all - критерий (число) Нуссельда (критерий теплоотдачи), характеризующий отношение

между интенсивностью теплоотдачи и температурным полем в пограничном слое. Чем больше значение критерия Нуссельда, тем интенсивнее процесс конвективного теплообмена.

Среди перечисленных критериев теплового подобия критерий Нуссельда определяемый, поскольку в него входит искомый коэффициент теплоотдачи, а остальные критерии определяющие.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Так как критерии гидродинамического и теплового подобия, определяемые из системы дифференциальных уравнений, описывающих конвективный теплообмен, одновременно являются критериями, получаемыми из решения системы уравнений, то критериальное уравнение конвективного теплообмена в общем виде можно записать следующим образом:

В случае стационарного процесса критерий Фурье из уравнения (2.61) исключается:

Опыты показывают, что критериальные уравнения могут быть представлены в виде степенных зависимостей.

В случае теплоотдачи при свободном движении (обогрев помещений, котельные агрегаты с естественной циркуляцией пароводяной смеси) можно пользоваться критериальным уравнением М.А. Михеева:

Значения констант С и m определяют из соответствующих таблиц в зависимости от значения произведения GrPr.

В случае теплоотдачи при вынужденном движении жидкости используется критериальное уравнение

типа

где C, m и n определяются по опытным данным в зависимости от условий эксперимента.

При ламинарном режиме течения жидкости рекомендуется следующее критериальное уравнение М.А. Михеева:

При турбулентном режиме течения жидкости рекомендуется следующее критериальное уравнение:

Таким образом, определив по одному из критериальных уравнений критерий Нуссельда, находим искомое значение коэффициента теплоотдачи, что в дальнейшем позволит определить остальные параметры процесса конвективного теплообмена.

Контрольные вопросы

1.Что понимается под конвективным теплообменом, теплоотдачей?

2.Запись основного уравнения теплоотдачи.

3.В каком случае понятии о подобии могут быть распространены на любые физические явления.

PDF created with pdfFactory Pro trial version www.pdffactory.com