
LARIONOV
.pdf
Основная инженерная задача, которая решается при исследовании процесса фильтрации, - это определение скорости движения жидкости сквозь фильтрующий материал, или нахождение фильтрационного расхода. Величина фильтрационного расхода зависит от свойств жидкости, структурой фильтрующего материала (размер пор и их форма, толщина материала и т.п.).
Движение жидкости происходит не сплошным потоком, а отдельными струйками по каналам, причем скорости отдельных струек могут существенно отличаться друг от друга из-за неоднородности пор и неравномерности их распределения в структуре материала, изменения формы и размеров поперечного сечения каналов. Очевидно, что данные факторы существенно усложняют решение задачи, но, тем не менее, она может быть решена двумя вариантами.
Решение по первому варианту может быть выполнено путем описания процесса фильтрации с использованием модели идеального фильтрующего материала, в котором фильтрующие каналы имеют цилиндрическую форму и расположены параллельно друг другу. Кроме этого, фильтрация в большинстве случаев происходит в условиях ламинарного режима, что позволяет использовать выражение (1.62) для определения скорости течения жидкости в одном фильтрующем канале:
V0 = 8pμтрl r2 ,
где r - радиус фильтрующего канала; pтр - потери давления по длине l фильтрующего канала.
Обозначив r2/8 = n0, получим V0 = nμ0 × plтр .
Скорость течения жидкости в одном фильтрующем канале можно связать со скоростью движения жидкости через весь фильтрующий материал следующим образом:
V = V m = |
mn |
× |
pтр |
= |
n |
× |
pтр |
|
|
0 |
|
|
|
, |
(1.84) |
||||
|
|
|
|
||||||
0 |
μ |
|
l |
|
μ |
|
l |
|
|
|
|
|
|
|
|
где m - так называемая пористость фильтрующего материала или отношение суммы объема всех пор ко всему объему фильтрующего материала. Коэффициент n = mn0, имеющий размерность площади, называется проницаемостью фильтрующего материала.
Фильтрационный расход находится умножением скорости фильтрации на площадь фильтрации:
Q = ωV = ω |
n |
× |
pтр |
. |
(1.85) |
|
|
||||
ф |
μ |
|
l |
|
|
|
|
|
|
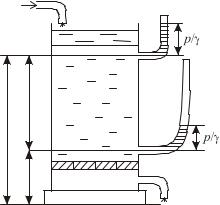
Решение по второму варианту может быть основано на опытах Дарси, в которых использовалось устройство, состоящее из вертикального цилиндрического сосуда, заполненного фильтрующим материалом (песком), через который при постоянной разности напора пропускалась жидкость (рис.1.17).
PDF created with pdfFactory Pro trial version www.pdffactory.com
L |
z1 |
z2 |
Рис.1.17. Опытная установка Дарси |
В различных точках по высоте цилиндрического сосуда установлены пьезометры для определения давления по высоте фильтрующего материала. Измеряемым параметром в опытах был расход фильтруемой жидкости, а варьируемыми параметрами - высота и пористость фильтрующего слоя.
На основании проведенных исследований Дарси установил закон фильтрации, которому подчиняется большинство несжимаемых жидкостей при своем движении через пористые среды.
Закон Дарси для фильтрационного расхода имеет следующее математическое выражение:
Q = kω |
hтр |
, |
(1.86) |
|
|||
ф |
l |
|
|
|
|
|
где Qф - фильтрационный расход; ω - площадь фильтрации, под которой понимается площадь поперечного сечения всего фильтрующего слоя, включая как сам фильтрующий материал, так и сумму площадей всех пор между отдельными частицами материала (в данном случае площадь поперечного сечения
тр |
|
ç |
1 |
|
÷ |
|
ç |
2 |
|
p2 |
÷ |
|
|
цилиндрического сосуда); h |
- потери напора при фильтрации, равные |
æ z |
+ |
p1 |
ö |
- |
æ z |
|
+ |
ö |
и |
||
γ ø |
|
γ |
|
||||||||||
|
|
è |
|
|
|
è |
|
|
ø |
|
|||
определяемые по разности показаний пьезометров; k - коэффициент фильтрации, характеризующий одновременно как фильтрационные свойства пористой среды, так и физические свойства фильтруемой жидкости; l - толщина слоя пористого материала в направлении фильтрации.
Соответственно средняя в сечении фильтрующего материала скорость фильтрации равна:
V = |
Qф |
= k |
hтр |
. |
(1.87) |
ω |
|
||||
|
|
l |
|
||
Из этого выражения видно, что коэффициент фильтрации имеет размерность скорости.
Как было определено раннее (1.52), отношение hтр/l представляет собой гидравлический уклон, поэтому выражение (1.87) можно представить в виде
V = |
Qф |
= ki . |
(1.88) |
|
|||
|
ω |
|
|
В дальнейшем скорость фильтрации стали определять не через потери напора, а через разность давлений, соответствующих этим потерям:
V = |
n |
× |
pтр |
. |
(1.89) |
|
μ |
l |
|||||
|
|
|
|
PDF created with pdfFactory Pro trial version www.pdffactory.com
В таком случае коэффициент фильтрации связан с проницаемостью фильтрующего материала
следующим соотношением: |
|
|
|
k = |
γn |
. |
(1.90) |
|
|||
|
μ |
|
|
Сделаем пояснение. Выражения для скорости фильтрации и фильтрационного расхода получены в предположении, что движение жидкости сквозь пористую среду происходило при ламинарном режиме, при котором скорость движения жидкости пропорциональна гидравлическому уклону в первой степени. При режиме течения жидкости, отличному от ламинарного, скорость пропорциональна гидравлическому уклону в степени, меньшей единицы. Поэтому в общем виде закон фильтрации можно записать как
|
1 |
|
|
V = |
Qф |
= kin . |
(1.91) |
|
|||
|
ω |
|
|
При этом n = 1 для ламинарного режима, 1 < n < 2 - для турбулентного режима.
В качестве примера использования приведенных кратких положений теории фильтрации рассмотрим движение жидкости в водонасыщенной пористой среде.
Все фильтрационные потоки делятся на напорные (без свободной поверхности) и безнапорные (со свободной поверхностью). Примерами напорных фильтрационных потоков могут служить артезианские подземные воды, которые при бурении скважин дают фонтан. При этом фильтрация происходит в пласте, заключенном между двумя непроницаемыми пластами без образования свободной поверхности. Примером безнапорных потоков является грунтовые воды, которые просачиваются в котлованы, траншеи, сквозь дамбы и плотины. Проницаемый пласт залегает на непроницаемом основании и не перекрывается сверху непроницаемым слоем. Фильтрация происходит с образованием свободной поверхности, давление на которой равно атмосферному.
Целью практических расчетов в данном случае являются:
-определение притока подземных вод к водозаборным сооружениям (колодцы, скважины и т.п.);
-проектирование систем фильтрации на станциях водоподготовки питьевой воды;
-выбор систем строительного водопонижения для котлованов, траншей или подземных проходок в водонасыщенных грунтах;
-проектирование дренажных систем, понижающих уровень грунтовых вод, для защиты подземных сооружений и помещений зданий от потопления.
1.5.2. Приток безнапорных вод к колодцу
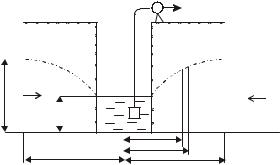
Положим, что в водоносном пласте толщиной (мощностью) H, расположенном на горизонтальном водонепроницаемом (водоупорном) слое, устроен водосборный колодец радиусом r (рис.1.18).
ст |
|
|
|
H |
д |
z |
z + dz |
|
H |
|
|
|
|
x |
|
|
L |
x + dx |
L |
|
|
||
|
Рис.1.18. Приток вод к колодцу |
||
PDF created with pdfFactory Pro trial version www.pdffactory.com

Если начать откачивать воду из колодца с постоянным расходом Q, то уровень воды в колодце будет понижаться. Поскольку в водоносном пласте уровень воды будет выше, чем в колодце, то из пласта вода начнет поступать в колодец, что приводит к понижению уровня грунтовых вод в пласте и это понижение будет максимальным у стенок колодца, постепенно убывая по мере удаления от стенок. При этом поступление воды будет тем больше, чем больше разность уровней в колодце и водоносном слое. При некотором значении этой разности наступит равновесие: количество воды, поступающей в колодец, будет равно количеству воды, откачиваемому из колодца.
Уровень воды в колодце до начала откачки, одинаковый с уровнем во всем водоносном слое, обычно называют статическим Hст. Уровень воды, устанавливающийся в колодце в процессе откачки, называют динамическим Нд, а кривая линия, образующаяся при сечении открытой поверхности уровня воды в пласте вертикальной плоскостью, проходящей через ось колодца, называется кривой депрессии, или кривой падения уровня.
На некотором расстоянии от оси колодца снижение уровня, вызываемое откачкой воды, становится практически незаметным, это расстояние называется радиусом дренированиия Rдр, или радиусом влияния колодца. При данных условиях необходимо определить зависимость расхода от радиуса колодца, мощности пласта и некоторых других параметров. Для этого проведем произвольным радиусом x соосную с колодцем цилиндрическую поверхность высотой z (см. рис.1.18). Площадь живого сечения потока к колодцу на расстоянии x от оси колодца равна 2πxz.
Далее проведем вторую соосную цилиндрическую поверхность радиусом x + dx и высотой z + dz. Допуская, что скорость фильтрации незначительна по величине, и пренебрегая в этом случае удельной кинетической энергией, получим, что потеря удельной энергии воды при прохождении расстояния dx между цилиндрами равна dz. Тогда потеря энергии на единицу длины (или гидравлический уклон) равна:
i = dxdz .
Из общего выражения закона Дарси (1.91) фильтрационная скорость определяется как
1
V= k æ dz ön
ç÷ , è dx ø
а фильтрационный расход -
1
Q= Vω = 2πxzk æ dz ön
ç÷ . è dx ø
Возводя последнее уравнение в n-ю степень и разделяя переменные, получаем
Qndx |
= (2πk)n zndz . |
(1.92) |
xn |
|
|
Интегрирование уравнения (1.92) будет различным в зависимости от численного значения n, которое, как уже отмечалось, определяется режимом течения жидкости.
При ламинарном режиме n = 1, тогда
Qdxx = 2πkzdz .
Интегрируя, получаем
Q ln x = πkz2 + C . |
(1.93) |
PDF created with pdfFactory Pro trial version www.pdffactory.com
При x = r z = Hд находим постоянную интегрирования
C = Q ln r − πkHд2 .
Тогда из (1.93) окончательно имеем |
|
|
|
|
Q ln |
x |
= πk (z2 − Hд2 ). |
(1.94) |
|
r |
||||
|
|
|
Выражение (1.94) представляет собой уравнение кривой депрессии. Учитывая, что при x = Rдр ордината z = Hст, получаем выражение для фильтрационного расхода:
Q = |
πk |
(Hст2 − Нд2 ) |
x . |
(1.95) |
|||||||||
|
|
ln |
Rдр |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
При n > 1 результаты интегрирования имеют вид |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
Q = 2πk |
|
(Hстn+1 − Hдn+1)(n −1) |
|
||||||||||
|
|
|
|
|
. |
|
|||||||
|
(r1−n − R1−n )(n +1) |
|
|||||||||||
|
|
|
|
|
|
др |
|
|
|
|
|
|
|
В частном случае, когда n = 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Q = 2πr |
|
Hст3 − Нд3 |
|
. |
(1.96) |
||||||||
|
3(r−1 − Rдр−1 ) |
||||||||||||
Величину Rдр на практике определяют опытным путем. При отсутствии опытных данных можно приблизительно принимать Rдр от 250 до 500 м для мелкозернистых песчаных грунтов и примерно до 700 м для крупнозернистых грунтов.
1.5.3. Приток безнапорных вод к водосборной траншее
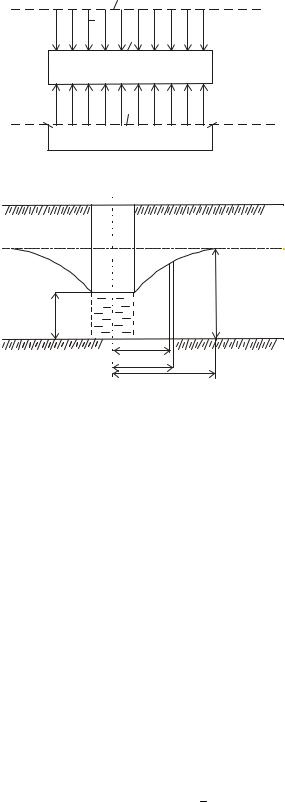
На рис.1.19 изображена водосборная траншея прямоугольного сечения длиной В, которая своим дном доходит до горизонтального водонепроницаемого слоя. Прибывающая в траншею вода откачивается насосом с расходом Q, при этом уровень воды в траншее начинает понижаться. При некотором понижении наступает равновесие:
количество воды, поступающее в траншею, равно количеству откачиваемой воды.
PDF created with pdfFactory Pro trial version www.pdffactory.com
3
2
1
2  3
3
B
а
z |
z+dz |
ст |
H |
||
x |
|
|
х+dх |
Rдр |
|
б |
|
|
Рис.1.19. Фильтрация в траншею: а - план; б - разрез (1 - траншея; 2 - направление фильтрации; 3 - граница области фильтрации)
Для получения зависимости расхода Q от толщины водоносного слоя Hст , глубины воды в траншее
Hд и других параметров проведем вертикальную плоскость на расстоянии x от стены траншеи. Площадь живого сечения потока определяется выражением ω = Bz, где z - ордината кривой дисперсии.
На расстоянии dx от первого сечения проведем второе сечение, для которого ордината кривой дисперсии будет z + dz. Поскольку величина скорости фильтрации незначительна, то можно считать, что потеря удельной энергии воды при прохождении расстояния dx равна dz. Отсюда гидравлический уклон
равен i = dz . |
|
|
|
dx |
|
|
|
æ dz ö |
1 |
|
|
n |
, а |
||
Тогда скорость фильтрации на данном участке определяется выражением V = k ç |
÷ |
|
|
è dx ø |
|
|
|
фильтрационный расход, или приток жидкости в траншею (с одной стороны),
1
Q= Vω = Вzk æ dz ön
ç÷ . è dx ø
Проводя вычислительные действия, аналогичные приведенным выше, получаем уравнение кривой дисперсии:
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
Bnkn (zn+1 |
- H n+1) |
|
|
Qn x = |
|
д |
.(1.97) |
|
n +1 |
||||
|
|
|||
Учитывая, что при x = L (где L - расстояние от стенки траншей до границы области фильтрации)
ордината z = Hст , выражение (1.97) примет вид |
|
|
|
|
|
|||
|
|
Bnk n (H n+1 |
- H n+1) |
|
||||
QnL = |
|
|
ст |
д |
|
|
||
|
|
|
n +1 |
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Q = Bk × n |
Hстn+1 - Hдn+1 |
. |
(1.98) |
|||||
(n +1)L |
||||||||
|
|
|
|
|
||||
При ламинарном режиме, когда n = 1, имеем |
|
|
|
|
|
|||
Q = |
|
Bk |
(Hст2 − Hд2 ) |
|
|
|||
|
|
|
|
. |
|
(1.99) |
||
|
|
2L |
|
|
||||
|
|
|
|
|
|
|
||
Удельный фильтрационный расход (на единицу длины траншеи) равен:
q = |
k (Hст2 |
− Hд2 ) |
. |
(1.100) |
|
|
|
||||
2L |
|||||
|
|
|
|||
С помощью выражения (1.100) можно определить количество воды, фильтрующейся через вертикальную стенку из мелкозернистого грунта (ламинарная фильтрация) (рис.1.20).
















 L
L







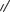


Рис.1.20. Фильтрация через вертикальную стенку
Как показывает практика, для определения количества воды, фильтрующейся через стенку трапециидальной формы (рис.1.21), можно принять L = b + 0,5Hст .
Рис.1.21. Фильтрация через трапециидальную стенку |
PDF created with pdfFactory Pro trial version www.pdffactory.com
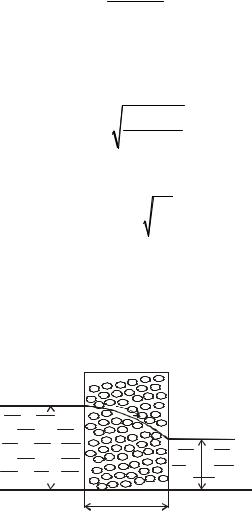
Тогда выражение (1.99) примет вид
Q = |
Bk (Hст2 |
- Hд2 ) |
||
|
|
|
. |
|
2b + H |
|
|||
|
ст |
|||
Если Hд2 мало по сравнению с Hст2 , то, пренебрегая Hст2 , получаем
BkН 2
Q = ст . (1.101)
2b + Hст
Последнее выражение можно использовать для определения количества воды, фильтрующейся через земляные плотины.
В случае турбулентного режима течения жидкости (n = 2) из выражения (1.98) получаем
Н 3 - Н 3
Q = Bk × ст д . (1.102)
3L
При Hд3 << Hст3 имеем
Q = BkНст × |
|
Н |
|
. |
(1.103) |
|
|||||
|
|
3L |
|
||
Выражение (1.103) определяет количество воды, фильтрующейся через вертикальную стенку из крупных камней (рис.1.22).
При определении количества воды, проходящей в виде фильтрата через дамбу из каменной насыпки, имеющей форму, близкую к трапециидальной, в выражении (1.103) можно с некоторым допущением принимать L равным ширине основания дамбы b.
ст |
д |
H |
H |
L
Рис.1.22. Фильтрация сквозь дамбу из каменной насыпки
1.5.4. Движение сквозь сетчатые фильтры
Для очистки воздушных потоков от содержащихся в них пылевидных частиц используются фильтры из различных сетчатых материалов, которые в данном случае являются местным гидравлическим сопротивлением. Потери напора в таком сопротивлении можно определить по формуле Вейсбаха:
h = ξ |
V 2 |
= ξ |
Q2 |
|
, |
(1.104) |
|
2g |
2gm2 |
ω2 |
|||||
|
|
|
|
PDF created with pdfFactory Pro trial version www.pdffactory.com
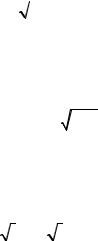
где ξ = |
92 - 78m + 0,71(1,05 - m) - |
|
коэффициент |
сопротивления |
сетки (приведенное выражение |
||||
|
Rea |
|
|
|
|
|
|
|
|
справедливо для сеток с квадратными ячейками); |
m = |
a2 |
- скважность сетки; а - размер стороны ячейки |
||||||
t2 |
|||||||||
|
|
|
|
|
|
|
|
||
сетки; |
t - шаг сетки; |
Rea = Va |
, |
где |
V |
- средняя |
скорость в ячейках сетки |
||
|
|
ν |
|
|
|
|
|
|
|
(V = V0/m; V0 - средняя скорость на подходе к сетке).
1.5.5. Безнапорное движение жидкости
Данный вид движения жидкости в инженерной практике реализуется в мелиоративных системах, системах водоотведения бытовых и промышленных сточных вод, системах отведения ливневых вод. Движение жидкости осуществляется либо в открытых каналах, либо по трубопроводам, работающим неполным сечением, при этом движение жидкости в основном является равномерным.
При равномерном движении жидкости средние скорости во всех поперечных сечениях потока равны между собой, поэтому равномерное движение при безнапорном движении возможно лишь тогда, когда форма и размеры поперечного сечения и уклон дна канала, шероховатость стенок остаются постоянными на всем пути движения жидкости.
При расчете равномерного безнапорного движения используется следующая формула для расчета средней скорости жидкости:
V = S |
i |
, |
(1.105) |
где S - скоростная характеристика; i - уклон дна, или гидравлический уклон, или уклон свободной поверхности.
Для определения скоростной характеристики может быть использовано выражение
æ |
R |
|
ö |
|
|
|
|
|
|
|
|
|
|
||||
S = ç1,81lg |
|
+ 2,73 |
÷ |
8gR , |
(1.106) |
|||
k |
||||||||
è |
|
ø |
|
|
|
|
||
здесь k - абсолютная шероховатость стенок канала; R - гидравлический радиус. Тогда расход жидкости при безнапорном движении равен:
Q = Sω |
i |
= K |
i |
, |
(1.107) |
где K = Sω - расходная характеристика.
Введем понятие гидравлически наивыгоднейшего профиля, при котором для заданных значений площади живого сечения, шероховатости стенок и уклона дна будет обеспечиваться наибольший расход жидкости.
Из выражений (1.106) и (1.107) видно, что при заданных значениях k, ω, i наибольший расход обеспечивается при наибольшем гидравлическом радиусе или при наименьшем смоченном периметре, что геометрически соответствует полукругу. Но в практике самотечного движения жидкости довольно часто используют русла трапециидальной формы. В этом случае наивыгоднейший профиль обеспечивается
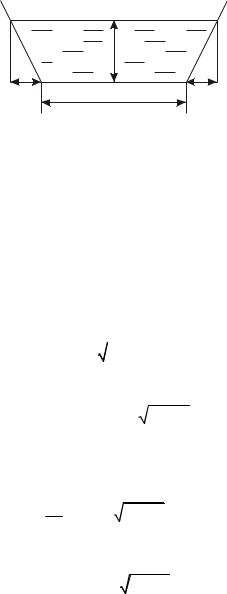
определенным соотношением между шириной дна русла и глубиной заполнения русла жидкостью
(рис.1.23).
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
h |
mh |
mh |
|
b |
Рис.1.23. К определению наивыгоднейшего профиля:
b - ширина дна канала; h - глубина заполнения; m - коэффициент откоса
Тогда из геометрии поперечного сечения русла площадь живого сечения равна:
ω = bh + mh2 , |
(1.108) |
откуда
b = |
ω |
− mh . |
(1.109) |
|
h |
|
|
Смоченный периметр находим из выражения
|
|
|
|
χ = b + 2h 1+ m2 . |
(1.110) |
||
Подставляя в (1.110) значение b из (1.109), имеем
χ = ωh − mh + 2h
 1+ m2 .
1+ m2 .
dχ
Приравняв производную dh к нулю, получим
−hω2 − m + 2
 1+ m2 = 0 .
1+ m2 = 0 .
Сиспользованием выражения (1.108) окончательно имеем
b |
= 2(−m + |
|
). |
|
1+ m2 |
(1.111) |
|||
h |
|
|
|
|
Данная формула определяет наивыгоднейшее соотношение между шириной дна канала и глубиной жидкости в нем.
Путем простых преобразований из приведенных выражений получаем, что в трапециидальных руслах при гидравлически наивыгоднейшем сечении гидравлический радиус равен половине глубины (R = h/2).
Контрольные вопросы
1.Причины потерь энергии при движении жидкости.
2.Основной закон для потерь на трение при равномерном движении жидкости.
3.Потери на трение при ламинарном режиме движения жидкости.
4.Формула Дарси - Вейсбаха.
5.Выражение для определения коэффициента гидравлического трения при ламинарном режиме движения жидкости.
6.Особенности турбулентного режима течения жидкости при определении потерь напора на трение.
7.Понятие гидравлически гладких и шероховатых труб.
PDF created with pdfFactory Pro trial version www.pdffactory.com
