LARIONOV

При стремлении размеров тетраэдра в пределе до нуля последний член выражения (1.20) также будет стремиться к нулю, а проекции гидростатических давлений будут оставаться конечными величинами.

Отсюда в пределе можно записать

По аналогии в проекциях на две другие координатные оси имеем py = pn, pz = pn. Окончательно имеем

Поскольку размеры тетраэдра были выбраны произвольно, то был произвольным и наклон площадки dω . Меняя ориентацию в пространстве площадки с изменением размеров граней тетраэдра, получим аналогичные результаты. В пределе, при стремлении размеров тетраэдра к точке, получим, что давление в этой точке будет одинаковым по всем направлениям.

Следствие: гидростатическое давление в точке будучи одинаковым по любому направлению различно в различных точка пространства, занимаемого жидкостью. Другими словами, гидростатическое давление является функцией координат p = f (x, y, z) .

1.2.4. Дифференциальное уравнение равновесного состояния жидкости (уравнение Эйлера)

Для вывода уравнения выделим внутри покоящейся жидкости элементарный объем в форме параллелепипеда с ребрами, параллельными координатным осям выбранной системы координат, и размерами dx, dy, dz (рис.1.3).

PDF created with pdfFactory Pro trial version www.pdffactory.com

O X

Z

Рис.1.3. К выводу дифференциального уравнения

равновесного состояния жидкости

Для выделенного параллелепипеда составим уравнение равновесия в виде проекции действующих сил на координатные оси: Σx = 0; Σy = 0; Σz = 0. Проецируя на ось ОХ, имеем

Выражая проекции сил через давления, действующие на соответствующие грани, получаем

dPABCD = pdydz; dPA′B′C′D′ = p′dydz; dFx = ρdxdydzX . (1.24)

Поскольку гидростатическое давление является функцией координат и при переходе от площадки

ABCD к площадке A′B′C′D′ меняется только координата х, то среднее гидростатическое давление на

После соответствующих преобразований получаем

−∂∂px + ρX = 0 .

Сучетом аналогичных вычислений для двух других координатных осей будем иметь следующую систему дифференциальных уравнений равновесия (гидростатики):

−∂∂px + ρX = 0,

PDF created with pdfFactory Pro trial version www.pdffactory.com

Умножая первое уравнение системы на dx , второе на dy , третье на dz и делая соответствующие преобразования, получаем уравнение, не содержащее частных производных и более удобное в практическом использовании:

Данное уравнение является основным дифференциальным уравнением гидростатики, определяющим приращение давления dp при изменении координат dx,dy, dz при равновесном состоянии жидкости.

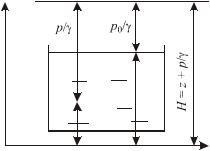
Рассмотрим равновесие жидкости в поле сил тяготения, т.е. на жидкость действует только сила тяжести вдоль оси Z.

Пусть произвольный объем жидкости, расположенный в незамкнутом сосуде, находится в состоянии равновесия. Свободная поверхность жидкости расположена на расстоянии z0 относительно произвольно

выбранной плоскости сравнения; давление на свободной поверхности равно p0 . Жидкость обладает

удельным весом γ . Требуется определить давление в точке М, расположенной на расстоянии z

относительно плоскости сравнения (рис.1.4). Очевидно, что для данного случая проекции массовой силы на координатные оси будут иметь следующие значения: X = 0, Y = 0, Z = –g.

Тогда из основного дифференциального уравнения гидростатики получаем

Плоскость гидростатического напора

Z

z0

M

z

X

Рис.1.4. К определению давления в точке М

Постоянную интегрирования найдем, используя параметры свободной поверхности z = z0 , p = p0 .

Данное уравнение называется основным уравнением гидростатики.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Представим уравнение (1.30) несколько в другом виде

Не трудно заметить, что все члены уравнения (1.31) имеют линейную размерность: z, z0 - координаты свободной поверхности и точки М; p0/γ, p/γ - высоты, соответствующие гидростатическому давлению на свободной поверхности и в точке М. В гидравлике величины z, p/γ принято называть геометрическими и пьезометрическими высотами или напорами соответственно. Сумма Н геометрического и пьезометрического напоров также имеет линейную размерность и ее называют гидростатическим напором. Из уравнения (1.31) следует, что для всех точек внутри покоящейся жидкости величина гидростатического давления есть величина постоянная. С геометрической точки зрения гидростатический напор представляет собой ординату горизонтальной плоскости, называемой плоскостью гидростатического напора и расположенной выше свободной поверхности на величину p0/γ.

Уравнению (1.31) можно придать энергетический смысл, если каждый член уравнения умножить на единичную силу 1 Н. Тогда все слагаемые приобретут размерность работы или энергии. Очевидно, что в этом случае уравнение (1.31) будет определять потенциальную энергию, подсчитанную для массы жидкости весом 1 Н. Будем называть эту энергию удельной энергией.

Тогда энергетическую интерпретацию уравнения (1.31) можно сформулировать следующим образом:

сумма удельной потенциальной энергии положения z и удельной потенциальной энергии давления p/γ есть величина постоянная во всех точках данной покоящейся жидкости.

1.2.5. Поверхность уровня

При решении целого класса прикладных задач гидравлики полезно пользоваться понятием поверхности уровня, все точки которой имеют одно и тоже значение рассматриваемой функции. Для гидравлики наибольший интерес представляет поверхность равного давления.

Уравнение поверхности равного давления можно получить из дифференциального уравнения гидростатики, учитывая, что во всех точках этой поверхности гидростатическое давление имеет одно и то же значение и следовательно dp = 0 . Тогда уравнение поверхности равного давления будет иметь вид

Поверхность равного давления обладает следующими свойствами:

1.Две поверхности равного давления не пересекаются между собой (доказывается методом от противного).

2.Внешние объемные силы направлены к поверхности уровня по нормали (дается без доказательства).

Контрольные вопросы

1.Сформулируйте определение понятия жидкости и назовите ее основные физические свойства.

2.Что закладывается в понятие идеальная жидкость?

3.Физический смысл понятия вязкости жидкости. Сформулируйте закон Ньютона о силе внутреннего

трения.

4.Что называется гидростатическим давлением? В каких единицах измеряется гидростатическое давление?

PDF created with pdfFactory Pro trial version www.pdffactory.com

5.Природа сил, действующих в покоящейся жидкости.

6.Запишите основное дифференциальное уравнение равновесия жидкости и следствие из него в виде основного уравнения гидростатики.

7.Определение понятия поверхности равного уровня и свойства поверхностей равного уровня.

1.3.Движение жидкости

1.3.1. Основные понятия и определения движения жидкости

Анализ процессов движения жидкости будем проводить (если это не будет оговариваться особо) для идеальной жидкости, основным критерием идеальности для которой будет отсутствие вязкости. Такая подвижная жидкость будет обладать рядом свойств реальной неподвижной жидкости: в ней возможен лишь один вид напряжения - нормальное напряжение сжатия или то же самое, что и гидромеханическое давление. Данное давление будет обладать в движущейся жидкости теми же свойствами, что и в реальной неподвижной: на внешней поверхности оно направлено по внутренней нормали, а в любой точке внутри жидкости - одинаково по всем направлениям.

Кроме этого, в настоящем пособии в основном будет рассматриваться стационарный режим течения, при котором давление и скорость являются функциями лишь координат и не зависят от времени, т.е.

p = f(x, y, z); V = f(x, y, z), при этом ∂∂pt = 0; ∂∂Vtx = 0;

∂Vy = 0; ∂Vz = 0 . ∂t ∂t

Дальнейшей степенью идеализации, принятой в гидравлике, является понятие о струйчатой структуре потока жидкости, в соответствии с которым поток представляется как совокупность элементарных струек, прилегающих вплотную друг к другу и образующих сплошную массу движущейся жидкости. В связи с этим вначале вводят понятие линии тока - такой линии, касательные к каждой точке которой совпадают с направлением вектора скорости в данной точке. При стационарном режиме течения жидкости линия тока совпадает с траекторией движения частицы жидкости.

Если внутри потока жидкости выделить бесконечно малый замкнутый контур и через каждую точку контура провести линию тока, то получим замкнутую поверхность, называемую трубкой тока. Часть потока жидкости, заключенная внутри трубки тока, называется элементарной струйкой. Таким образом,

элементарная струйка оказывается изолированной от остальной массы жидкости и является непроницаемой для жидкости, т.е. ни одна частица жидкости не может выйти наружу из трубки тока и ни одна частица не может проникнуть внутрь трубки тока извне. Длина элементарной струйки не ограничена, а площадь ее поперечного сечения может меняться по длине, при этом ввиду малости поперечного сечения элементарной струйки скорость во всех точках этого сечения можно считать одинаковой.

Скорость частицы жидкости может меняться по длине элементарной струйки или оставаться постоянной. В первом случае имеем неравномерное течение жидкости, во втором - равномерное. Для

возможности сравнительного анализа равномерного и неравномерного течения жидкости введем понятие расхода жидкости.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Пусть в некотором поперечном сечении элементарной струйки площадью dω скорость жидкости

равна V. За элементарный отрезок времени dt частицы жидкости переместятся на расстояние ds = Vdt.

В силу сплошности жидкой среды следующие за ними частицы жидкости заполнят все освободившее пространство. Таким образом, за указанный отрезок времени через поперечное сечение элементарной струйки пройдет объем жидкости, равный dW = dsdω = Vdωdt .

Объем жидкости, протекающий через поперечное сечение элементарной струйки в единицу времени,

принято называть объемным расходом жидкости. Обычно его обозначают через dQ . Тогда имеем

Исходя из условия сплошности среды, можно заключить, что объемные расходы в различных сечениях по длине элементарной струйки будут равны. Данное положение называется уравнением расхода для

элементарной струйки и записывается в виде

Алгебраическая сумма расходов всех элементарных струек, составляющих данный поток, будет

представлять собой объемный расход потока

i=1

Ранее было условлено, что в силу малости поперечного сечения элементарной струйки скорость жидкости во всех точках поперечного сечения одинакова. Но при этом скорость жидкости в различных элементарных струйках, составляющих поток, может быть различной. Для характеристики движения всего потока вводят в рассмотрение среднюю (одинаковую по всему сечению потока) скорость, которая

определяется выражением

В системах вентиляционных воздуховодов и водоотведения часто применяют трубопроводы не круглого сечения. В этом случае при проведении гидравлических расчетов для характеристики размеров и формы поперечного сечения потока вводится понятие живого сечения, смоченного периметра и гидравлического радиуса.

Живым сечением потока (площадью живого сечения ω) называется площадь сечения трубопровода, проведенного нормально к направлениям линий тока (нормально к направлениям скоростей элементарных струек) и заполненного жидкостью. Живое сечение может быть ограничено твердыми стенами трубопровода полностью или частично (в этом случае часть живого сечения ограничивается открытой поверхностью жидкости). Если стенки трубопровода ограничивают поток полностью, то движение жидкости в этом случае называют напорным. Если же ограничение частичное, то движение называют безнапорным. Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока в общем случае отлично от атмосферного и может быть как больше, так и меньше последнего. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному давлению. Примером напорного движения может служить движение жидкости при ее перекачке по трубопроводу за счет энергии, создаваемой насосом. Примером безнапорного движения может служить движение жидкости в открытых каналах, реках.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Часть периметра живого сечения, по которому поток жидкости соприкасается с ограничивающими его стенками, называют смоченным периметром χ . Для круглого трубопровода в случае напорного движения смоченный периметр равен длине окружности, в случае безнапорного движения - длине дуги поверхности, по которой жидкость соприкасается со стенками трубопровода, так как свободная поверхность, по которой жидкость соприкасается с воздухом, в длину смоченного периметра не входит.

Отношение площади живого сечения к смоченному периметру называют гидравлическим радиусом сечения:

Следует иметь в виду, что гидравлический радиус и геометрический радиус - разные понятия. При напорном движении жидкости в круглом трубопроводе диаметром d геометрический радиус r = d/2, а гидравлический R = d/4.

Кроме этих понятий, в инженерной практике гидравлических расчетов используют понятие эквивалентного диаметра, который вычисляется с помощью следующего выражения:

1.3.2. Уравнение Бернулли для элементарной струйки идеальной жидкости

Уравнение Бернулли, помимо уравнения расхода, является основным уравнением гидродинамики,

устанавливающим зависимость между скоростью и давлением в различных сечениях одной и той же элементарной струйки жидкости.

Выделим в потоке жидкости одну из элементарных струек и сечениями 1 - 1 и 2 - 2 ограничим в ней участок произвольной длины (рис.1.5).

Для первого сечения зададим следующие параметры: площадь dω1 , скорость V1 в сечении и давление p1 , центр тяжести сечения расположен относительно произвольной плоскости сравнения на расстоянии z1 .

Для второго сечения соответственно имеем dω2 ,V2 , p2 , z2 . Под действием внешних сил за бесконечно малый промежуток времени выделенный участок переместится в положение 1′ - 2′.

Z

1

2

p2

2'

X

Рис.1.5. К выводу уравнения Бернулли

Применим к выделенному участку элементарной струйки теорему механики о том, что работа внешних сил, приложенных к телу, равна приращению кинетической энергии этого тела, т.е. Авн = Еk. В нашем

PDF created with pdfFactory Pro trial version www.pdffactory.com

случае внешними силами будут силы давления, действующие по нормали к поверхности выделенного участка элементарной струйки, и массовые силы в виде силы тяжести, которые и производят работу:

Работа сил давления складывается из работы в первом и втором сечениях, а также работы на боковой

Силы давления, действующие на боковую поверхность, работы не производят, поскольку они действуют по нормали к этой поверхности, а следовательно, и по нормали к направлению перемещения жидкости. Таким образом,

Работа массовых сил (силы тяжести) пропорциональна изменению потенциальной энергии положения выделенного участка элементарной струйки. Для нахождения этого изменения необходимо из потенциальной энергии положения жидкости в объеме 1 - 2 вычесть потенциальную энергию положения жидкости в объеме 1′ - 2′. При таком вычитании потенциальная энергия положения объема жидкости 1 - 2′ сократится. Поэтому в расчетах будет присутствовать лишь разность потенциальной энергии положения объемов 1 - 1′ и 2 - 2′. Используя уравнение расхода, нетрудно заметить, что объемы, а следовательно, и веса участков элементарной струйки 1 - 1′ и 2 - 2′ равны. Тогда можно записать

где γ - удельный вес жидкости.

В таком случае работу сил тяжести можно записать как

Для определения приращения кинетической энергии выделенного участка элементарной струйки за тот же самый отрезок времени dt следует из кинетической энергии объема 1′ - 2′ вычесть кинетическую энергию объема 1 - 2: Eк = Eк1′-2′ − Eк1-2 . Руководствуясь теми же соображениями, что и при подсчете потенциальной энергии, в результате получаем

Подставляя выражения для работы сил давления, силы тяжести и приращения кинетической энергии в исходное уравнение, имеем

PDF created with pdfFactory Pro trial version www.pdffactory.com

Разделив все члены уравнения (1.47) на dG и сделав соответствующие преобразования, в итоге

получим

Группируя члены с одноименными индексами и учитывая, что сечения в элементарной струйке идеальной жидкости выбраны произвольно, имеем

Полученное уравнение (1.49) называется уравнением Бернулли; входящие в него члены имеют линейную размерность и в гидравлике обозначают: z - нивелирная высота, или геометрический напор; p/γ -

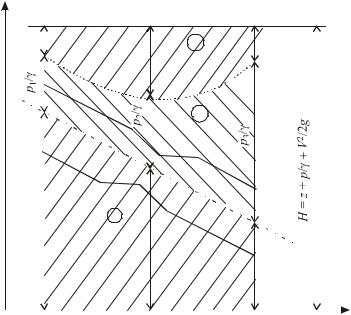
С геометрической точки зрения уравнение Бернулли говорит о том, что сумма трех напоров - геометрического, пьезометрического и скоростного есть величина постоянная вдоль элементарной струйки идеальной жидкости (рис.1.6). На рисунке можно выделить три характерные линии и области:

∙I-я область, расположенная между линией, соединяющей центры сечений идеальной струйки (линия геометрического напора), и линией сравнения, - зона изменения геометрического напора;

∙II-я область, расположенная между линией геометрического напора и линией пьезометрического напора, - область изменения пьезометрического напора;

∙III-я зона, расположенная между пьезометрической линией и линией скоростного напора, - область изменения скоростного напора.

Полный напор Н в уравнении Бернулли можно рассматривать как полную удельную энергию (т.е. энергию, отнесенную к единице веса) жидкости в данном сечении элементарной струйки. Тогда входящие в него члены являются удельной энергией положения, удельной энергией давления и удельной кинетической энергией. В соответствии с этим с энергетической точки зрения уравнение Бернулли можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия (сумма удельной энергии положения, удельной энергии давления и удельной кинетической энергии) есть величина постоянная во всех сечениях по длине струйки.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Рис.1.6. Геометрическая интерпретация уравнения Бернулли

1.3.3. Уравнение Бернулли для элементарной струйки реальной жидкости

Движение реальной жидкости (жидкости, обладающей вязкостью) сопровождается возникновением касательных напряжений. Это приводит к тому, что полная удельная энергия, или полный напор Н, не остается постоянной по длине струйки, а убывает по направлению движения. Причиной этого являются неизбежные потери энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости. Поэтому для элементарной струйки реальной жидкости полная удельная энергия в

Бернулли для реальной жидкости эти потери энергии выражаются через потери напора, а оно приобретает следующий вид:

где å h1−2 - сумма потерь напора при переходе от сечения 1 - 1 к сечению 2 - 2 элементарной струйки реальной жидкости.

1.3.4. Уравнение Бернулли для потока реальной жидкости

Как отмечалось выше, поток жидкости может быть представлен совокупностью отдельных элементарных струек, в каждой из которых скорость жидкости имеет свое значение. Поэтому при переходе от элементарной струйки к потоку реальной жидкости, имеющему конечные размеры, необходимо прежде всего учитывать неравномерность распределения скоростей по поперечному сечению потока. Для облегчения анализа процесса движения потока жидкости вводят допущение о том, что по поперечному

PDF created with pdfFactory Pro trial version www.pdffactory.com