
- •43 Пособие по практике аг
- •Прочти, реши и опять прочти!..
- •Содержание:
- •Занятие 1. Декартовы координаты. Векторы и скаляры. Сложение и вычитание векторов. Действия над векторами, заданными своими проекциями. Скалярное произведение векторов. Направление вектора.
- ••◄ Дополнительно ►•
- •Занятие 2. Определители 2-го порядка и системы линейных уравнений с двумя неизвестными. Определители 3-го порядка. Простейшие правила вычисления определителей.
- ••◄ Дополнительно ►•
- ••◄ Дополнительно ►•
- •Занятие 6. Контрольная работа №1. Прием части-1 бдз.
- •Занятие 7. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Общие свойства кривых второго порядка.
- •Занятие 8. Поверхности 2-го порядка. Канонические уравнения поверхностей 2-го порядка.
- ••◄ Дополнительно ►•
•◄ Дополнительно ►•
Пример
7–218
Куб
![]() задан своими вершинами:
задан своими вершинами:
![]() =(0,0,0),
=(0,0,0),
![]() =(1,0,0),
=(1,0,0),
![]() =(1,1,0),
=(1,1,0),
![]() =(0,1,0),
=(0,1,0),
![]() =(0,0,1),
=(0,0,1),
![]() =(1,0,1),
=(1,0,1),
![]() =(1,1,1),
=(1,1,1),
![]() =(0,1,1).
Выполнить следующие действия: а)
написать уравнения прямых линий
=(0,1,1).
Выполнить следующие действия: а)
написать уравнения прямых линий
![]() и
и
![]() ;
;
б)
вычислить расстояние между прямыми
линиями
![]() и
и
![]() ;
;
в ) написать
уравнение общего перпендикуляра между
прямыми линиями
) написать
уравнение общего перпендикуляра между
прямыми линиями
![]() и
и
![]() .
.
Решение:
Общее: хотя в геометрии чертёж обычно предназначен только для иллюстрации рассуждений, в рассматриваемом примере с помощью чертежа все задания можем легко выполнить, глядя на чертёж!
Для случая а):
1). Обозначим
прямую линию
![]() как
как
![]() .
Её направляющий вектор
.
Её направляющий вектор
![]() =
=![]() =(1,1,–1).
Учитывая, что прямая линия содержит
точку
=(1,1,–1).
Учитывая, что прямая линия содержит
точку
![]() =
=![]() =(0,0,1),
записываем каноническое уравнение этой
прямой
=(0,0,1),
записываем каноническое уравнение этой
прямой
![]() :
:
![]() .
.
2). Обозначим
прямую линию
![]() как
как
![]() .
Её направляющий вектор
.
Её направляющий вектор
![]() =
=![]() =(0,1,1).
Учитывая, что точка
=(0,1,1).
Учитывая, что точка
![]() =
=![]() =(1,0,0),
принадлежит
=(1,0,0),
принадлежит
![]() ,
записываем каноническое уравнение этой
прямой
,
записываем каноническое уравнение этой
прямой
![]() :
:
![]() .
.
Для случая б):
1). Так
как векторы
![]() и
и
![]() не параллельны, то
не параллельны, то
![]() и
и
![]() – скрещивающиеся прямые. Расстояние
между ними определяется формулой:
– скрещивающиеся прямые. Расстояние
между ними определяется формулой:
![]() .
.
2). Вычислим:
![]() =
=![]() x
x![]() =
=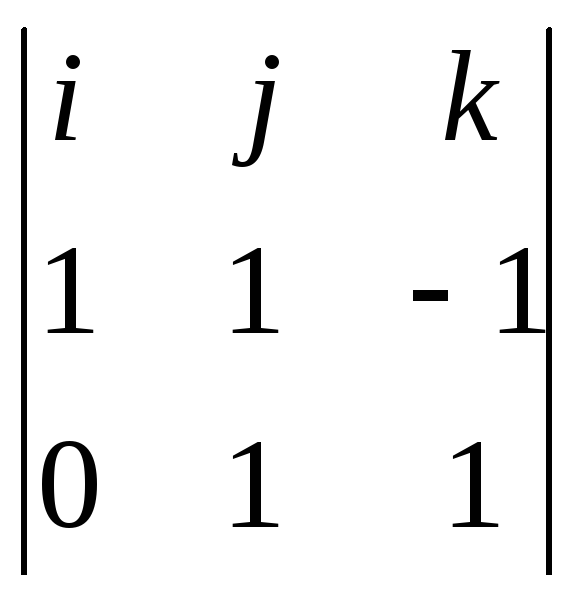 =
=![]() ∙
∙![]() –
–![]() ∙j
+
∙j
+![]() ∙k
=(2,–1,1)
→
∙k
=(2,–1,1)
→
![]() =
=![]() .
Вычислим вектор
.
Вычислим вектор
![]() =
=![]() =
=![]() =(1,0,–1).
Вычислим:
=(1,0,–1).
Вычислим:
![]() =
= =1.
Тогда можем вычислить:
=1.
Тогда можем вычислить:
![]() =
=![]() .
.
Для случая в):
1 ). Для
удобства воспользуемся рисунком, который
не привязан к кубу: просто имеются
скрещивающиеся прямые
). Для
удобства воспользуемся рисунком, который
не привязан к кубу: просто имеются
скрещивающиеся прямые
![]() и
и
![]() ,
и требуется получить уравнение их общего
перпендикуляра: обозначен как прямая
линия
,
и требуется получить уравнение их общего
перпендикуляра: обозначен как прямая
линия
![]() .
Обозначим направляющий вектор прямой
.
Обозначим направляющий вектор прямой
![]() как
как
![]() .
Он совпадает с вектором
.
Он совпадает с вектором
![]() =(2,–1,1).
=(2,–1,1).
2). Теперь наметим укрупнённый алгоритм решения задачи:
▫ строим
плоскость
![]() ,
содержащую точку
,
содержащую точку
![]() и вектор нормали
и вектор нормали
![]() =
=![]() ;
;
▫ находим
точку
![]() пересечения плоскости
пересечения плоскости
![]() с прямой
с прямой
![]() ;
;
▫ имея
точку
![]() и вектор
и вектор
![]() ,
получаем уравнение для прямой линии
,
получаем уравнение для прямой линии
![]() .
.
Реализуем намеченный алгоритм:
3). Вычислим
для плоскости
![]() вектор нормали
вектор нормали
![]() =
=![]() =
= =(–2,
–2,2), примем (удобнее) за вектор нормали
коллинеарный
=(–2,
–2,2), примем (удобнее) за вектор нормали
коллинеарный
![]() =(1,1,–1).
Используя точку
=(1,1,–1).
Используя точку
![]() =(1,0,0)
и вектор
=(1,0,0)
и вектор
![]() ,
запишем
,
запишем
![]() :
:![]() =
0, или
=
0, или
![]() :
:
![]() =0.
=0.
4). Из
уравнения прямой линии
![]() :
:
![]() запишем
запишем
![]() =
=![]() =
=![]() ,
,
![]() =
=![]() .
Из условия
.
Из условия
![]() =
=![]() можем записать:
можем записать:
![]() =0,
откуда получаем
=0,
откуда получаем
![]() =
=![]() и
и
![]() =
=![]() .
Теперь можем записать уравнение
.
Теперь можем записать уравнение
![]() :
:
 .
.
Замечание:
в связи с используемым
в задачнике ответом, который выражен
как линия пересечения плоскостей
![]() и
и
![]() ,
полезно получить результат:
,
полезно получить результат:
![]() =
=![]() .
.
6). Вычислим
для плоскости
![]() вектор нормали
вектор нормали
![]() =
=![]() =
= =(0,–3,–3),
примем (удобнее) за вектор нормали
коллинеарный
=(0,–3,–3),
примем (удобнее) за вектор нормали
коллинеарный
![]() =(0,1,1).
Используя точку
=(0,1,1).
Используя точку
![]() =(0,0,1)
и вектор
=(0,0,1)
и вектор
![]() ,
запишем
,
запишем
![]() :
:![]() =
0, или
=
0, или
![]() :
:
![]() =0.
=0.
7). В этом
случае имеем
![]() :
:
![]() .
Видим, что в задачнике плоскость
.
Видим, что в задачнике плоскость
![]() записана с
погрешностью.
Проверка показывает, что точка
записана с
погрешностью.
Проверка показывает, что точка
![]() не удовлетворяет второму уравнению!
не удовлетворяет второму уравнению!
Ответ:
в случае: а)
![]() :
:
![]() ,
,
![]() :
:
![]() ;
б)
;
б)
![]() =
=![]() ;
в)
;
в)
![]() :
:
 .
.
☻
Вопросы для самопроверки:
-
При помощи какого свойства векторов получают общее уравнение плоскости?
-
Как записывается уравнение плоскости, проходящей через заданную точку?
-
Что значит «уравнение плоскости в отрезках»?
-
Как получают каноническое уравнение прямой линии в пространстве?
-
Какой физический смысл имеет параметрическое задание уравнения прямой в пространстве?
-
Как получают уравнение прямой, проходящей через две заданные точки?
-
Что такое «отклонение» точки от заданной плоскости, как его вычисляют?
-
Как нормализовать общее уравнение плоскости?
-
Как определить угол между заданными прямыми линиями в пространстве?
-
Как записывают условия параллельности и перпендикулярности для двух прямых в пространстве?
-
Какие задачи в пространстве вызвали наибольший интерес (восторг!)?
Задачи для самоподготовки:
Пример
C5–1:
Составить уравнение
плоскости, которая проходит через точки
![]() и
и
![]() параллельно вектору
параллельно вектору
![]() ,
в случае: а)
,
в случае: а)
![]() (1,2,0),
(1,2,0),
![]() (2,1,1),
(2,1,1),
![]() =(3,0,1);
б)
=(3,0,1);
б)
![]() (1,1,1),
(1,1,1),
![]() (2,3,–1),
(2,3,–1),
![]() =(0,–1,2).
=(0,–1,2).
Ответ:
в случае: а)
![]() :
:
![]() =0;
б)
=0;
б)
![]() :
:
![]() =0.
=0.
Пример
C5–2:
Заданы две плоскости
![]() :
:
![]() =0
и
=0
и
![]() :
:
![]() =0.
Определить их взаимное расположение:
пересекаются, параллельны или совпадают.
Найти расстояние между плоскостями и
косинус угла между ними.
=0.
Определить их взаимное расположение:
пересекаются, параллельны или совпадают.
Найти расстояние между плоскостями и
косинус угла между ними.
Ответ:
плоскости параллельны, расстояние
между ними:
![]() =
=![]() .
.
Пример
C5–3:
Заданы две плоскости
![]() и
и
![]() .
Написать уравнение плоскости
.
Написать уравнение плоскости
![]() ,
равноудалённой от заданных плоскостей.
Рассмотреть случаи:
,
равноудалённой от заданных плоскостей.
Рассмотреть случаи:
а)
![]() :
:
![]() =0
и
=0
и
![]() :
:
![]() =0;
=0;
б)
![]() :
:
![]() =0
и
=0
и
![]() :
:
![]() =0.
=0.
Ответ:
в случаях: а)
![]() :
:
![]() =0;
б)
=0;
б)
![]() :
:
![]() =0.
=0.
Пример
C5–4:
Определить, лежат
ли точки
![]() (2,–1,1)
и
(2,–1,1)
и
![]() (1,2,–3)
в одном, в смежных или вертикальных
углах, образованных при пересечении
двух плоскостей, Для случая: б)
(1,2,–3)
в одном, в смежных или вертикальных
углах, образованных при пересечении
двух плоскостей, Для случая: б)![]() :
:![]() =0
и
=0
и
![]() :
:
![]() .
.
Ответ:
в случае б)
точки
![]() ,
,![]() расположены в вертикальных углах.
расположены в вертикальных углах.
Пример
C5–5:
Составить
каноническое уравнение прямой линии,
проходящей через точки
![]() и
и
![]() .
Рассмотреть случаи: а)
.
Рассмотреть случаи: а)
![]() (1,–2,1),
(1,–2,1),
![]() (3,1,–1);
б)
(3,1,–1);
б)
![]() (3,–1,0),
(3,–1,0),
![]() (1,0,–3).
(1,0,–3).
Ответ:
в случае: а)
![]() :
:
![]() ,
б)
,
б)
![]() :
:![]() .
.
< * * * * * >
